FIFEI08 Hydrostatika a hydrodynamika http stein upce czmsfei

FIFEI-08 Hydrostatika a hydrodynamika http: //stein. upce. cz/msfei 16. html http: //stein. upce. cz/fei/f. Ifei_08. html Doc. Miloš Steinhart, UPCE 06 036, ext. 6029 26. 04. 2016 1

Hlavní body • Úvod do hydrostatiky ideálních kapalin • Archimédův zákon. • Úvod do hydrodynamiky ideálních kapalin • Popis proudící kapaliny – zákony zachování • Množství • Hybnosti • Energie – Bernoulliho rovnice. • Exkurze do problematiky reálných kapalin • Newtonovské kapaliny - viskozita • ne-Newtonovské kapaliny, viskoelastické chování 26. 04. 2016 2

Tlak v kapalině I Pascalův zákon • V důsledku neexistence tečných napětí působí v každém bodě pouze tlak (=normálové napětí) a je stejný ze všech směrů. • Na tomto principu je založena např. hydraulika. Můžeme-li zanedbat vlastní tíhu kapaliny, je tlak v ní všude stejný a na různě velké plochy tedy působí různě velká síla: F 1/S 1 = p 2 = F 2/S 2 26. 04. 2016 3

Tlak v kapalině II • Předpokládejme • gravitační pole v blízkosti povrchu Země. = gz • osa z je svislá a její kladná část míří vzhůru. • Obecně musíme připustit závislost hustoty na z, potom : 26. 04. 2016 4

Tlak v kapalině III Průběh tlaku v kapalině je lineární • U těžko stlačitelných kapalin lze hustotu považovat za konstantní a tedy : • Integrace vede na lineární pokles tlaku s výškou : • Často uvažujeme naopak vzrůst s hloubkou pod hladinou: 26. 04. 2016 5

Tlak v kapalině IV Průběh tlaku s výškou v atmosféře je exponenciální • Předpokládejme izotermickou atmosféru, stlačitelnou podle Boyle-Marriotova zákona • Potom : • Diferenciální rovnici řešíme integrací po separaci proměnných a po odlogaritmování: 26. 04. 2016 6

Archimédův zákon I • Těleso ponořené do tekutiny je nadlehčováno silou, která se rovná tíze tekutiny tělesem vytlačené. • Nadlehčování je způsobeno tlakovými silami, které se snaží tekutinu “vrátit”, do míst, odkud byla tělesem vytlačena nebo kam se může alespoň principiálně dostat. • Protože tlak roste s hloubkou, lze očekávat, že výslednice sil bude směřovat vzhůru. 26. 04. 2016 7

Archimédův zákon II • Archimédův zákon • úzce souvisí s růstem tlaku s hloubkou • lze ilustrovat na tělese speciálního tvaru nebo • dokázat obecně jako rovnováhu objemových a povrchových sil. Druhý důkaz nepožaduje konstantní hustotu, čili nezávisí na možné stlačitelnosti tekutiny a platí tedy i pro plyny a také tělesa, která mohou být v několika prostředích, např. neúplně ponořená. 26. 04. 2016 8

Archimédův zákon III • Mějme rotační válec o výšce h a podstavě S v ideální kapalině o hustotě 0. • Tlakové síly na plášť se v každé hloubce vyrovnají. • Nevykompenzovaná zůstane pouze tlaková síla působící na spodní podstavu a tedy vzhůru, protože tato podstava je hlouběji o výšku válce než podstava horní: F = Sh 0 g. • To je ale přesně tíha vytlačené kapaliny. 26. 04. 2016 9

Archimédův zákon IV • V kapalině, která je v rovnováze si mysleme její určitý objem libovolného tvaru. • Tento objem má svoji hmotnost, a tíha směřuje svisle dolů. • Na povrch objemu působí tlakové síly. Protože je objem v rovnováze, musí jejich výslednice vykompenzovat tíhu, čili musí směřovat svisle vzhůru a její velikost se musí rovnat tíze myšleného objemu. 26. 04. 2016 10

Povrchové napětí I • Částice kapaliny blízko rozhraní mají ve svém okolí prostředí dvojího druhu. To obecně vede k nesymetrii působících sil, jak dovedeme vysvětlit opět pomocí potenciálové jámy. • Takový efekt existuje i na rozhraní dvou pevných látek. Jak jsme poznali, rozhraní kapaliny se vyznačuje tím, že zaujímá v každém bodě směr kolmo k působící síle. 26. 04. 2016 11

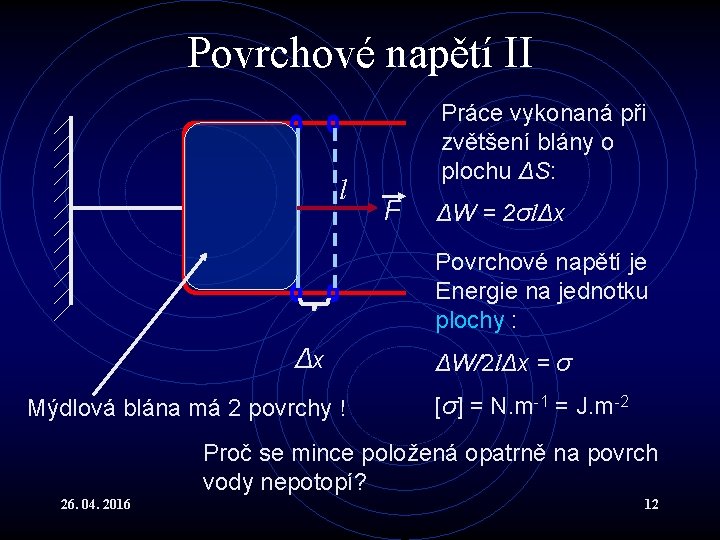
Povrchové napětí II l Práce vykonaná při zvětšení blány o plochu ΔS: F ΔW = 2σlΔx Povrchové napětí je Energie na jednotku plochy : Δx Mýdlová blána má 2 povrchy ! ΔW/2 lΔx = σ [σ] = N. m-1 = J. m-2 Proč se mince položená opatrně na povrch vody nepotopí? 26. 04. 2016 12

Povrchové napětí III • Například na rozhraní kapalina – plyn působí síly směřující do kapaliny. • Výsledkem je, že se rozhraní snaží zaujímat minimální povrch, např. se tvoří kapky. • Na rozhraní kapalina – pevná látka mohou síly směřovat : • do kapaliny - kapalina látku nesmáčí • z kapaliny ven - kapalina látku smáčí. 26. 04. 2016 13

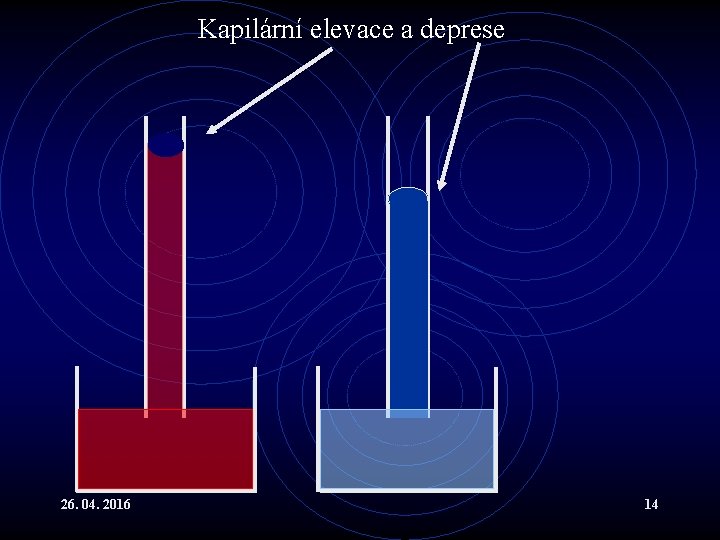
Kapilární elevace a deprese 26. 04. 2016 14

Úvod do hydrodynamiky • Popsat tekutiny v pohybu patří mezi nejobtížnější problémy, které v klasické fyzice existují. • Pro jednoduchost vyjdeme ze zákonů zachování, které platí pro pomalé proudění neviskózní a nestlačitelné kapaliny. • Později podrobněji popíšeme chování nejjednodušší viskózní, tzv. Newtonovské kapaliny a ukážeme příklady chování některých ne -Newtonovských kapalin. 26. 04. 2016 15

Hydrokinematika I • Proudící kapalinu lze popsat pomocí : • Trajektorií, křivek, po nichž se částice pohybují v čase. Částicí se zde rozumí makroskopicky malý ale mikroskopicky velký objem kapaliny. • Proudnic, křivek tečných v každém bodě k vektorům rychlosti. Proudnice tvoří proudové trubice, jejichž stěnami kapalina neprochází. Jejich vnitřek se nazývá proudová vlákna. 26. 04. 2016 16

Základní zákony zachování • U stacionárně proudících ideálních kapalin lze jednoduše využít zákonů zachování. Zachovávají se : • Množství – rovnice kontinuity • Hybnost • Energie – Bernoulliho rovnice 26. 04. 2016 17

Rovnice kontinuity • Časový objemový průtok Q kapaliny určitou proudovou trubicí se zachovává. Jinak by se kapalina musela někde objevovat nebo mizet. • Má-li proudová trubice u nestlačitelné kapaliny v jednom místě průřez S 1 a v druhém S 2, platí : S 1 v 1 = Q 2 = S 2 v 2 • U stlačitelných tekutin je konstantní průtok množství neboli hmotnosti a platí : S 1 v 1 1 = S 2 v 2 2 26. 04. 2016 18

Zachování hybnosti • Ke změně směru proudové trubice může dojít jen v případě existuje-li impuls síly, který příslušnou změnu hybnosti umožní : • Proudnice musí často podpírat navíc i rozdíl sil tlakových. • Změna rychlosti vede k nové rovnováze. 26. 04. 2016 19

Zachování energie • Bernoulliho rovnice vyjadřuje zákon zachování hustoty energie : • V praxi se vyjadřuje několika způsoby, například v rozměrech délkových : 26. 04. 2016 20

Odvození Bernoulliho rovnice I • Uvažujme dvě různá místa, ohraničující určitý úsek jedné proudové trubice. V každém je jistá rychlost vi, tlak pi a výška hi (i = 1, 2). • Na objemy působí z vnějšku úseku tlakové síly opačné orientace Fi = Si pi. • Působením těchto sil se za čas t přemístí určitý objem V s hmotností m z prvního místa do druhého. • Práce, kterou vykonají tyto síly za t se musí rovnat přírůstku celkové energie daného objemu. 26. 04. 2016 21

Odvození Bernoulliho rovnice II • Tedy : • Po dosazení : • Aplikujme rovnici kontinuity : 26. 04. 2016 22

Odvození Bernoulliho rovnice III • Tento vztah, vyjadřující zachování energie, bývá zvykem vztáhnout ke jednotkovému objemu, tedy vydělit V a přeskupit podle uvažovaných míst : • Vztah odvodil Švýcar Daniel Bernoulli 1700 -1783 • Celková energie proudící kapaliny má tedy tři složky : tlakovou, kinetickou a potenciální. 26. 04. 2016 23

Použití Bernoulliho rovnice I Výtok kapaliny otvorem • Bernoulliho rovnice lze použít jako prvního přiblížení při řešení řady praktických problémů. • Uvažujme například výtok kapaliny ze široké (nebo doplňované) nádoby malým otvorem umístěným v hloubce h pod hladinou. V Bernoulliho rovnici můžeme udělat několik úprav a zanedbání : 26. 04. 2016 24

Použití Bernoulliho rovnice II • Oba tlaky jsou atmosférické : p 1= p 2. • Vyjádříme hloubku otvoru : h = z 1 – z 2 • Je-li možné rychlost v 1 zanedbat. • Dostaneme po zkrácení a úpravě : Tento vztah se nazývá Torrichellio vzorec a je zajímavé, byl znám již sto let před Bernoullim. 26. 04. 2016 25

Použití Bernoulliho rovnice III • Není-li možné rychlost v 1 zanedbat, použijeme rovnici kontinuity v 1 = v 2 S 2/S 1 : • Po zkrácení , zavedení hloubky a úpravě : (výraz má zjevně smysl jen pro S 1 > S 2) 26. 04. 2016 26

Použití Bernoulliho rovnice IV Hydrodynamický paradoxon • Uvažujeme-li místa o stejné výšce je z Bernoulliho rovnice patrná zajímavá vlastnost proudících tekutin a to, že v místech s větší rychlostí je nižší tlak. Na tomto principu je založena řada jevů od bouchání dveří v průvanu, přes střílení rohového kopu ve fotbale, po létání letadel. Protože jsou důsledky na první pohled překvapivé, je tento jev znám jako hydrodynamický paradoxon. • Významné je jeho využití při měření rychlosti. 26. 04. 2016 27

Použití Bernoulliho rovnice V Pitotova trubice • Pitotova trubice (fajfka) : • do měřené kapaliny jsou vnořeny dvě trubice, ústí jedné je kolmo, ústí druhé rovnoběžně s jejím proudem (fajfka) v 2 = 0. • v i-té trubici vystoupí kapalina do výšky zi, odpovídající tlaku pi = gzi při jejím ústí • ve vztahu vystupuje pouze rozdíl výšek zi. • Používá se k měření rychlosti malých letadel. 26. 04. 2016 28

Použití Bernoulliho rovnice VI Venturiho trubice • Venturiho trubice (potřebuje zúžení) : • do měřené kapaliny jsou kolmo vnořeny dvě trubice, jedna v místě s průřezem S 1, druhá S 2. • v i-té trubici vystoupí kapalina opět do výšky zi, odpovídající tlaku pi = gzi při jejím ústí 26. 04. 2016 29

Použití Bernoulliho rovnice VII • Z obou rovnic : • Pro rychlost v 1 a průtok Q platí po úpravě : 26. 04. 2016 30

Viskózní kapaliny I Newtonova kapalina • Při proudění reálných tekutin se sousední vrstvy ovlivňují tečným napětím, které závisí na vzájemné rychlosti vrstev a viskozitě tekutiny. • Mějme tekutinu proudící ve směru osy x. Potom pro tečné napětí, čili napětí působící ve směru proudění, platí Newtonův zákon: 26. 04. 2016 31

Viskózní kapaliny II dynamická viskozita (éta) – míra odporu tečení [ ] = kg m-1 s-1 = Nm-2 s = Pa s Starší jednotka Poise [P]=gcm-1 s-1=0. 1 Pa s Převrácená hodnota se nazývá tekutost: = 1/ • Často se používá viskozita vztažená na hustotu, tzv. kinematická viskozita (ný) = / • D je gradient rychlosti rovný časové změně deformace ve střihu. • • 26. 04. 2016 32

Viskózní kapaliny III • Pro lepší ilustraci fyzikálního významu viskozity uvažujme například válcovou nádobu s míchadlem a Newtonův zákon ve tvaru : • Má-li se míchadlo točit vždy stejnou rychlostí je pro viskóznější kapalinu potřeba většího momentu síly a tedy i výkonu motoru. • Totéž je potřeba, chceme-li pro určitou konkrétní kapalinu zvýšit rychlost míchání. 26. 04. 2016 33

Viskózní kapaliny IV • Dynamická a kinematická viskozita některých kapalin: • • • ETOH rtuť benzín olej voda 26. 04. 2016 (éta) [Pa s] 1. 2 10 -3 1. 5 10 -3 2. 9 10 -4 2. 6 10 -2 1. 005 10 -3 (ný) [m 2/s] 1. 51 10 -6 1. 16 10 -7 4. 27 10 -7 2. 79 10 -4 8. 04 10 -7 34

Viskózní kapaliny V • Viskozita : • snižuje průtok kapaliny (za daných podmínek) • způsobuje, že rychlost v protékaném průřezu není konstantní, ale má určité rozložení, u krajů je minimální (nulová) a uprostřed maximální. • Ukážeme, že v (proudové) trubici kruhového průřezu je rozložení rychlosti na vzdálenosti od osy parabolické. 26. 04. 2016 35

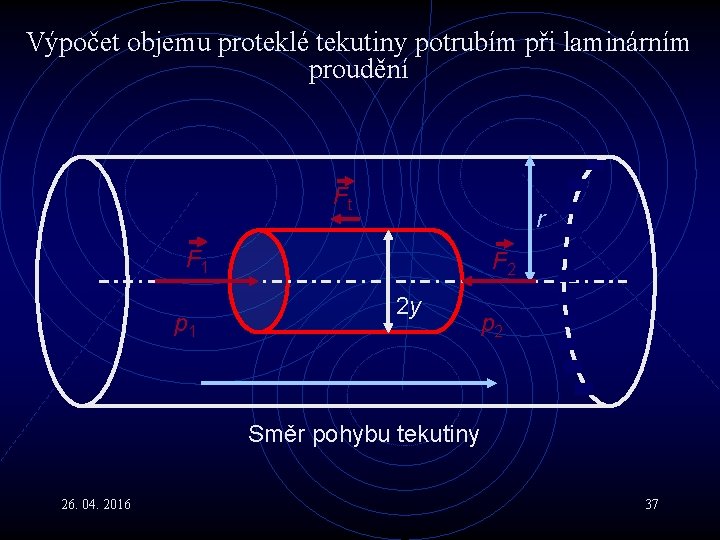
Viskózní kapaliny VI • Mysleme si v laminárně a rovnoměrně proudící kapalině váleček o poloměru y. Na • podstavy působí tlakové síly (p 1 > 0, p 2 < 0) • plášť síla způsobená třením okolních vrstev. • Pohybuje-li se válec rovnoměrně, musí být všechny síly na něj působící, tedy síly působící na podstavy plus na plášť v rovnováze : 26. 04. 2016 36

Výpočet objemu proteklé tekutiny potrubím při laminárním proudění Ft r F 1 p 1 F 2 2 y p 2 Směr pohybu tekutiny 26. 04. 2016 37

Viskózní kapaliny VIII • Předpokládejme, že p 1 > p 2 a tedy kapalina se pohybuje ve směru růstu souřadnice x. • Znaménko + by znamenalo, že by třecí síla měla směr rychlosti. • Protože první člen je kladný, musí být třecí síla záporná, čili brzdící a rychlost klesá směrem od osy. 26. 04. 2016 38

Viskózní kapaliny IX • Po zavedení p = p 1 – p 2 a úpravě : • Po integraci : 26. 04. 2016 39

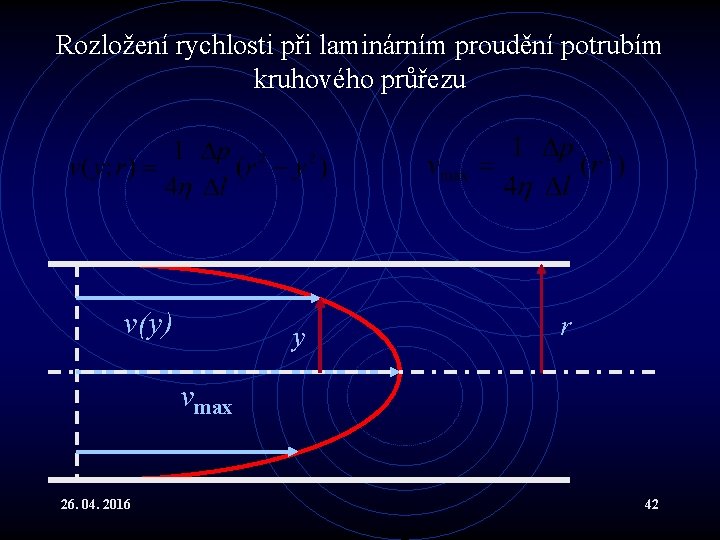
Viskózní kapaliny X • Uvažujeme-li trubici o poloměru r. Obdržíme hodnotu integrační konstanty k z okrajové podmínky v(r) = 0 : • a celkově dostáváme parabolickou závislost : 26. 04. 2016 40

Viskózní kapaliny XI • Důležitou a snadněji měřitelnou veličinou je průtok. Celkový průřez musíme rozdělit na mezikruží o poloměru y, v nichž je vždy rychlost konstantní: • Celkový průtok obdržíme integrací : • To je známá Hagen-Poiseuillova rovnice. 26. 04. 2016 41

Rozložení rychlosti při laminárním proudění potrubím kruhového průřezu v(y) y r vmax 26. 04. 2016 42

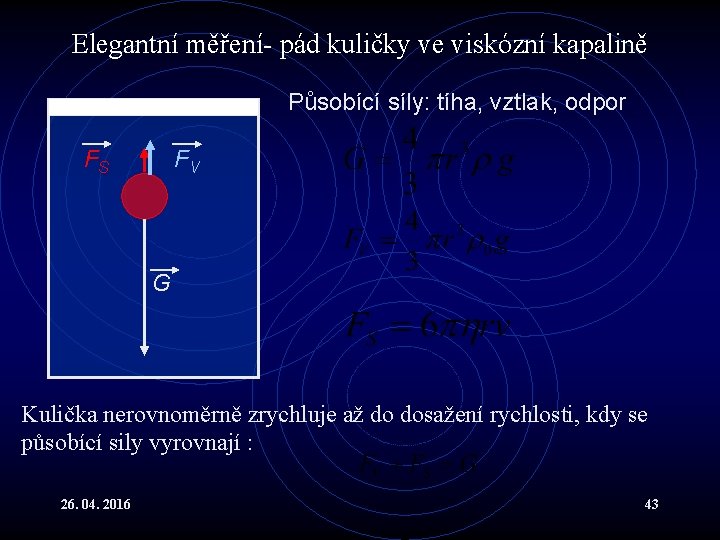
Elegantní měření- pád kuličky ve viskózní kapalině Působící síly: tíha, vztlak, odpor FS FV G Kulička nerovnoměrně zrychluje až do dosažení rychlosti, kdy se působící sily vyrovnají : 26. 04. 2016 43

Viskózní kapaliny XIV • Stokesův zákon: • Na kuličku o poloměru r, která se pohybuje malou rychlostí v v kapalině působí brzdící síla F = 6 rv • Kulička o hustotě bude po ustálení rovnováhy padat v kapalině 0 konstantní rychlostí vt : 26. 04. 2016 44

Viskózní kapaliny XV • Laminární proudění • brzdící síla je úměrná rychlosti • rychlost je úměrná r 2 • střední rychlost vyplývající z H-P rovnice <v>=Qv/S je také úměrná r 2 a tlakovému spádu • Za mezí Stokesova zákona : • Často je brzdící síla úměrná v 2 : Fd = Cd. Sv 2 • Cd je parametr, který závisí na tvaru 26. 04. 2016 45

Viskózní kapaliny XVI • Pro posouzení, zda je proudění ještě laminární se používá tzv. Reynoldsovo číslo. • pro kuličku o poloměru r, pohybující se rychlostí v • pro kapalinu pohybující se střední rychlostí <v> v trubici o poloměru r platí : (ve jmenovateli posledního výrazu je řecké (ný), tedy kinematická viskozita!) • Pro R >1000 (v velké) je proudění turbulentní • Při R –> 0 (r malé a/nebo velké) se systémy chovají značně nestandardně. 26. 04. 2016 46

*Dynamika krevního oběhu I Na základě práce Dr. J. Tulky • Krevní oběh je udržován srdcem. Levá část síň -> komora pumpuje krev do velkého (tělního) oběhu a pravá část do malého oběhu (plic). • Krev v aortě : • <v> = 0. 3 ms-1 • r = 0. 01 m • = 1060 kg m-3 • = 3. 3 10 -3 Pa s • R 970 proudění je těsně ještě laminární. 26. 04. 2016 47

* Dynamika krevního oběhu II • Ve velkých žilách proudí krev pomaleji, jen rychlostí <v> = 0. 1 ms-1 a ve vlásečnicích dokonce jen rychlostí <v> = 0. 001 ms-1. Pomocí rovnice kontinuity můžeme odhadnout, že celkový průřez • vlásečnic je 300 krát větší než průřez aorty • velkých žil je 3 krát větší než průřez aorty 26. 04. 2016 48

* Dynamika krevního oběhu III • Podle H-P zákona je tlakový spád nepřímo úměrný čtvrté mocnině poloměru trubice. K největšímu spádu tedy musí docházet v arteriální sekci : • aorta plicnice • systola 16 k. Pa (120 torr) 3. 3 k. Pa • diastola 10. 5 k. Pa (80 torr) 1. 3 k. Pa 26. 04. 2016 49

* Dynamika krevního oběhu IV • Práce srdce bývá vyjadřována jako součet • statické – objemové dodávající tlakovou energii • kinetické – dodávající kinetickou energii odpovídající příslušné střední rychlosti : • Pro střední hodnoty V = 70 ml a p = 13. 3 k. Pa je Wo= 0. 93 J a Wk= 0. 003 J, tedy W = 0. 94 J 26. 04. 2016 50

* Dynamika krevního oběhu V • Práce pravé komory je asi jedna pětina práce komory levé. Celková mechanická práce srdce při jedné systole je tedy asi 1. 13 J. • Při tepové frekvenci 70 min-1 je výkon srdce přibližně 1. 3 W. • Tato hodnota představuje jen asi jednu desetinu celkového mechanického výkonu srdce. Převažující část se spotřebuje na udržování stálého napětí (tonusu) srdeční svaloviny. 26. 04. 2016 51

* Dynamika krevního oběhu VI • Celkový srdeční výkon je tedy 13 W, což představuje přibližně 13% celkového klidového výkonu organismu. • Srdce ale funguje nepřetržitě řadu let. Za 60 let života vykoná práci 2. 5 GJ, což je : • 3 s výkonu Chvaletické elektrárny • Vyzdvižení 30 t břemene na Mt. Everest 26. 04. 2016 52

Základy reologie I • Reologie se zabývá deformacemi látek za reálných podmínek • Tyto deformace mohou být obecně velmi komplikované a záviset na mnoha faktorech. Proto je reologie velice rozsáhlá a otevřená oblast výzkumu. • Zde uvedeme příklad chování některých ne. Newtonovslých kapalin a visko-elastického chování. • S. Pirkl : “Reologie a reometrie kapalin” 26. 04. 2016 53

Základy reologie II • Ideálně může být deformace • elastická – při ní se těleso po odstranění napětí vrátí do původního stavu a nedochází ke ztrátám energie – modelujeme pružinou • plastická – po odstranění napětí zůstává trvalá deformace a dochází ke ztrátám energie – modelujeme tělesem, které táhneme se třením • viskózní tečení – trvalá deformace je velká – modelujeme nádobou s perforovaným pístem • Reálné deformace jsou zpravidla jejich kombinací 26. 04. 2016 54

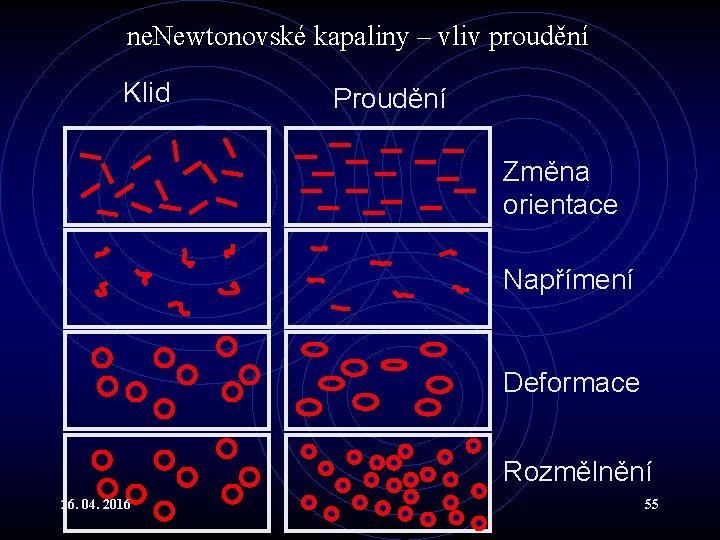
ne. Newtonovské kapaliny – vliv proudění Klid Proudění Změna orientace Napřímení Deformace Rozmělnění 26. 04. 2016 55

Typy ne-Newtonovských kapalin • Pseudoplastické - viskozita klesá s rostoucím gradientem rychlosti • Dilatantní - viskozita roste s rostoucím gradientem rychlosti • Binghamské – k toku dochází po překročení určitého smykového napětí Tokové křivky Newtonovská τ dv/dy 26. 04. 2016 56

Základy reologie III • Zdánlivá viskozita může záviset také na době namáhání. Tokové křivky mají potom hysterezní chování. Příkladem jsou látky: • tixotropní – u nichž viskozita s časem klesá • reopektické – u nichž viskozita s časem roste 26. 04. 2016 57

Základy reologie IV • Visko-elastické chování se často měří při namáhání látky harmonickým napětím. Odezva bude také harmonická, ale následkem ztrát fázově zpožděná. Můžeme ji tedy charakterizovat komplexním modulem. Jeho reálná část odpovídá elastickému chování a imaginární ztrátám. • Existuje také např. visko-plastické chování. 26. 04. 2016 58

Deformace • Odezva látek je vždy úměrná rozměru před deformací, proto je užitečné ji k tomuto původním rozměru vztáhnout. Podle typu deformace používáme například relativní • prodloužení • • Střih dx dy • stlačení 26. 04. 2016 v 59

Skalární součin Ať Definice I (ve složkách) Definice II Skalární součin je součin velikosti jednoho vektoru krát průmět velikosti vektoru druhého do jeho směru. 26. 04. 2016 60 ^

Příklad - potenciál I • Spočítejme práci, kterou musíme (jako vnější činitel) dodat pro přemístění hmotnosti m z r. A do r. B v centrálním poli jisté hmotnosti M. • Závisí jen na vzdálenostech od tělesa a práci musíme dodávat jen při zvětšování r, protože působíme proti přitažlivé síle. 26. 04. 2016 61

Příklad - potenciál II Tuto práci chápeme jako přírůstek potenciální energie srovnáním 26. 04. 2016 62

Příklad - potenciál III • Práce dodaná tělesu vnějším činitelem zvýší jeho potenciální energii. Tu obecně definujeme včetně integrační konstanty C, dané kalibrací: • Často předpokládáme, že potenciální energie v nekonečnu je nulová, což odpovídá C=0 : 26. 04. 2016 ^ 63

Gradient I Je vektor sestrojený z diferenciálů funkce f ve směrech jednotlivých souřadných os. Je používán k odhadu změny funkce f provedeme-li elementární posun. 26. 04. 2016 64

Gradient II Změna je druhý člen. Je to skalární součin. K největší změně dochází, je-li elementární posun paralelní ke směru gradientu. Jinými slovy má gradient směr největší změny funkce f ! 26. 04. 2016 ^ 65

První kosmická rychlost pro Měsíc Takové rychlosti může dosáhnout speciální střela a rozhodně také molekuly plynu, který by tvořil atmosféru Měsíce. Proto Měsíc atmosféru nemá a ani by se ji tam nepodařilo vytvořit. 26. 04. 2016 ^ 66

Relativistické efekty při urychlování elektronu • Relativistické efekty se začínají výrazněji projevovat, dosáhne-li rychlost c/10= 3 107 ms-2. • Jaké urychlovací napětí je potřebné k dosažení této rychlosti ? • Ze zachování energie : mv 2/2 = q U U=mv 2/2 e=9 1014/4 1011= 2. 5 k. V ! 26. 04. 2016 ^ 67

Dvě 1 g Fe kuličky, 1 m od sebe se přitahují silou 10 N. Jaký je jejich přebytečný náboj? Přebytečný náboj : Celkový a přebytečný /celkový náboj : 26. 04. 2016 ^ 68

Korekce g na rotaci Země I Srovnejme tíhu tělesa na pólu a na rovníku : 26. 04. 2016 ^ 69

Korekce g na rotaci Země II Přesný výpočet vyžaduje vzít v úvahu zploštění Země, na rovníku cca 21 km. V zeměpisných šířkách mezi rovníkem a pólem je nutno vzít v úvahu i fakt, že odstředivé zrychlení působí kolmo k ose otáčení, takže výsledné tíhové zrychlení nesměřuje přesně do středu Země. 26. 04. 2016 ^ 70