Exponents and Polynomials Sections 12 1 Exponents 12




























































- Slides: 60

Exponents and Polynomials

Sections 12. 1 – Exponents 12. 2 – Negative Exponents and Scientific Notation 12. 3 – Introduction to Polynomials 12. 4 – Adding and Subtracting Polynomials 12. 5 – Multiplying Polynomials 12. 6 – Special Products 12. 7 – Dividing Polynomials Steven Bangirana-0786 404202 2

Exponents

Exponents that are natural numbers are shorthand notation for repeating factors. 34 = 3 • 3 • 3 3 is the base 4 is the exponent (also called power) Note by the order of operations that exponents are calculated before other operations. Steven Bangirana-0786 404202 4

Evaluating Exponential Expressions Example Evaluate each of the following expressions. 34 = 3 • 3 • 3 = 81 (– 5)2 = (– 5) = 25 – 62 = – (6)(6) = – 36 (2 • 4)3 = (2 • 4)(2 • 4) = 8 • 8 = 512 3 • 42 = 3 • 4 = 48 Steven Bangirana-0786 404202 5

Evaluating Exponential Expressions Example Evaluate each of the following expressions. a. ) Find 3 x 2 when x = 5. 3 x 2 = 3(5)2 = 3(5 · 5) = 3 · 25 = 75 b. ) Find – 2 x 2 when x = – 1. – 2 x 2 = – 2(– 1)(– 1) = – 2(1) = – 2 Steven Bangirana-0786 404202 6

The Product Rule (applies to common bases only) am · an = am+n Example Simplify each of the following expressions. 32 · 34 = 32+4 = 36 = 3 · 3 · 3 · 3= 729 x 4 · x 5 = x 4+5 = x 9 z 3 · z 2 · z 5= z 3+2+5 = z 10 (3 y 2)(– 4 y 4) = 3 · y 2 (– 4) · y 4 = 3(– 4)(y 2 · y 4) = – 12 y 6 Steven Bangirana-0786 404202 7

The Power Rule (am)n = amn Example Simplify each of the following expressions. (23)3 = 23· 3 = 29 = 512 (x 4)2 = x 4· 2 = x 8 Steven Bangirana-0786 404202 8

The Power of a Product Rule (ab)n = an · bn Example Simplify (5 x 2 y)3 = 53 · (x 2)3 · y 3 = 125 x 6 y 3 Steven Bangirana-0786 404202 9

The Power of a Quotient Rule Example Simplify (5 x 2 y)3 = 53 · (x 2)3 · y 3 = 125 x 6 y 3 Steven Bangirana-0786 404202 10

The Power of a Quotient Rule Example Simplify the following expression. (Power of product rule) (Power rule) Steven Bangirana-0786 404202 11

The Quotient Rule (applies to common bases only) Example Simplify the following expression. Group common bases together Steven Bangirana-0786 404202 12

Zero Exponent Zero exponent a 0 = 1, a 0 Note: 00 is undefined. Example Simplify each of the following expressions. 50 = 1 (xyz 3)0 = x 0 · y 0 · (z 3)0 = 1 · 1 = 1 –x 0 = –(x 0) = – 1 Steven Bangirana-0786 404202 13

Negative Exponents and Scientific Notation

Negative Exponents Using the quotient rule from section 3. 1, But what does x -2 mean? Steven Bangirana-0786 404202 15

Negative Exponents So, in order to extend the quotient rule to cases where the difference of the exponents would give us a negative number we define negative exponents as follows. If a 0, and n is an integer, then Steven Bangirana-0786 404202 16

Simplifying Expressions Example Simplify by writing each of the following expressions with positive exponents or calculating. Remember that without parentheses, x is the base for the exponent – 4, not 2 x Steven Bangirana-0786 404202 17

Simplifying Expressions Example Simplify by writing each of the following expressions with positive exponents or calculating. Notice the difference in results when the parentheses are included around 3. Steven Bangirana-0786 404202 18

Simplifying Expressions Example Simplify by writing each of the following expressions with positive exponents. 1) 2) (Note that to convert a power with a negative exponent to one with a positive exponent, you simply switch the power from a numerator to a denominator, or vice versa, and switch the exponent to its positive value. ) Steven Bangirana-0786 404202 19

Summary of Exponent Rules If m and n are integers and a and b are real numbers, then: Product Rule for exponents am · an = am+n Power Rule for exponents (am)n = amn Power of a Product (ab)n = an · bn Power of a Quotient Rule for exponents Zero exponent a 0 = 1, a 0 Negative exponent Steven Bangirana-0786 404202 20

Simplifying Expressions Simplify by writing the following expression with positive exponents or calculating. Power of a quotient rule Power rule for exponents Power of a product rule Quotient rule for exponents Negative exponents Steven Bangirana-0786 404202 Negative exponents 21

Scientific Notation In many fields of science we encounter very large or very small numbers. Scientific notation is a convenient shorthand for expressing these types of numbers. A positive number is written in scientific notation if it is written as a product of a number a, where 1 a < 10, and an integer power r of 10. a 10 r Steven Bangirana-0786 404202 22

Scientific Notation To Write a Number in Scientific Notation 1) Move the decimal point in the original number to the left or right, so that the new number has a value between 1 and 10. 2) Count the number of decimal places the decimal point is moved in Step 1. • If the original number is 10 or greater, the count is positive. • If the original number is less than 1, the count is negative. 3) Multiply the new number in Step 1 by 10 raised to an exponent equal to the count found in Step 2. Steven Bangirana-0786 404202 23

Scientific Notation Example Write each of the following in scientific notation. Have to move the decimal 3 places to the left, so that the 1) 4700 new number has a value between 1 and 10. Since we moved the decimal 3 places, and the original number was > 10, our count is positive 3. 4700 = 4. 7 103 2) 0. 00047 Have to move the decimal 4 places to the right, so that the new number has a value between 1 and 10. Since we moved the decimal 4 places, and the original number was < 1, our count is negative 4. 0. 00047 = 4. 7 10 -4 Steven Bangirana-0786 404202 24

Scientific Notation To Write a Scientific Notation Number in Standard Form • Move the decimal point the same number of spaces as the exponent on 10. • If the exponent is positive, move the decimal point to the right. • If the exponent is negative, move the decimal point to the left. Steven Bangirana-0786 404202 25

Scientific Notation Example Write each of the following in standard notation. 1) 5. 2738 103 Since the exponent is a positive 3, we move the decimal 3 places to the right. 5. 2738 103 = 5273. 8 2) 6. 45 10 -5 Since the exponent is a negative 5, we move the decimal 5 places to the left. 00006. 45 10 -5 = 0. 0000645 Steven Bangirana-0786 404202 26

Operations with Scientific Notation Multiplying and dividing with numbers written in scientific notation involves using properties of exponents. Example Perform the following operations. 1) (7. 3 10 -2)(8. 1 105) = (7. 3 · 8. 1) (10 -2 · 105) = 59. 13 103 = 59, 130 2) Steven Bangirana-0786 404202 27

Introduction to Polynomials

Polynomial Vocabulary Term – a number or a product of a number and variables raised to powers Coefficient – numerical factor of a term Constant – term which is only a number Polynomial is a sum of terms involving variables raised to a whole number exponent, with no variables appearing in any denominator. Steven Bangirana-0786 404202 29

Polynomial Vocabulary In the polynomial 7 x 5 + x 2 y 2 – 4 xy + 7 There are 4 terms: 7 x 5, x 2 y 2, -4 xy and 7. The coefficient of term 7 x 5 is 7, of term x 2 y 2 is 1, of term – 4 xy is – 4 and of term 7 is 7. 7 is a constant term. Steven Bangirana-0786 404202 30

Types of Polynomials Monomial is a polynomial with 1 term. Binomial is a polynomial with 2 terms. Trinomial is a polynomial with 3 terms. Steven Bangirana-0786 404202 31

Degrees Degree of a term To find the degree, take the sum of the exponents on the variables contained in the term. Degree of a constant is 0. Degree of the term 5 a 4 b 3 c is 8 (remember that c can be written as c 1). Degree of a polynomial To find the degree, take the largest degree of any term of the polynomial. Degree of 9 x 3 – 4 x 2 + 7 is 3. Steven Bangirana-0786 404202 32

Evaluating Polynomials Evaluating a polynomial for a particular value involves replacing the value for the variable(s) involved. Example Find the value of 2 x 3 – 3 x + 4 when x = 2. 2 x 3 – 3 x + 4 = 2( 2)3 – 3( 2) + 4 = 2( 8) + 6 + 4 = 6 Steven Bangirana-0786 404202 33

Combining Like Terms Like terms are terms that contain exactly the same variables raised to exactly the same powers. Warning! Only like terms can be combined through addition and subtraction. Example Combine like terms to simplify. x 2 y + xy – y + 10 x 2 y – 2 y + xy = x 2 y + 10 x 2 y + xy – 2 y (Like terms are grouped together) = (1 + 10)x 2 y + (1 + 1)xy + (– 1 – 2)y = 11 x 2 y + 2 xy – 3 y Steven Bangirana-0786 404202 34

Adding and Subtracting Polynomials

Adding and Subtracting Polynomials Adding Polynomials Combine all the like terms. Subtracting Polynomials Change the signs of the terms of the polynomial being subtracted, and then combine all the like terms. Steven Bangirana-0786 404202 36

Adding and Subtracting Polynomials Example Add or subtract each of the following, as indicated. 1) (3 x – 8) + (4 x 2 – 3 x +3) = 3 x – 8 + 4 x 2 – 3 x + 3 = 4 x 2 + 3 x – 8 + 3 = 4 x 2 – 5 2) 4 – (– y – 4) = 4 + y + 4 = y + 8 3) (– a 2 + 1) – (a 2 – 3) + (5 a 2 – 6 a + 7) = – a 2 + 1 – a 2 + 3 + 5 a 2 – 6 a + 7 = – a 2 + 5 a 2 – 6 a + 1 + 3 + 7 = 3 a 2 – 6 a + 11 Steven Bangirana-0786 404202 37

Adding and Subtracting Polynomials In the previous examples, after discarding the parentheses, we would rearrange the terms so that like terms were next to each other in the expression. You can also use a vertical format in arranging your problem, so that like terms are aligned with each other vertically. Steven Bangirana-0786 404202 38

Multiplying Polynomials

Multiplying Polynomials Multiplying polynomials • • If all of the polynomials are monomials, use the associative and commutative properties. If any of the polynomials are not monomials, use the distributive property before the associative and commutative properties. Then combine like terms. Steven Bangirana-0786 404202 40

Multiplying Polynomials Example Multiply each of the following. 1) (3 x 2)(– 2 x) = (3)(– 2)(x 2 · x) = – 6 x 3 2) (4 x 2)(3 x 2 – 2 x + 5) = (4 x 2)(3 x 2) – (4 x 2)(2 x) + (4 x 2)(5) = 12 x 4 – 8 x 3 + 20 x 2 (Distributive property) (Multiply the monomials) 3) (2 x – 4)(7 x + 5) = 2 x(7 x + 5) – 4(7 x + 5) = 14 x 2 + 10 x – 28 x – 20 = 14 x 2 – 18 x – 20 Steven Bangirana-0786 404202 41

Multiplying Polynomials Example Multiply (3 x + 4)2 Remember that a 2 = a · a, so (3 x + 4)2 = (3 x + 4) = (3 x)(3 x + 4) + 4(3 x + 4) = 9 x 2 + 12 x + 16 = 9 x 2 + 24 x + 16 Steven Bangirana-0786 404202 42

Multiplying Polynomials Example Multiply (a + 2)(a 3 – 3 a 2 + 7) = a(a 3 – 3 a 2 + 7) + 2(a 3 – 3 a 2 + 7) = a 4 – 3 a 3 + 7 a + 2 a 3 – 6 a 2 + 14 = a 4 – a 3 – 6 a 2 + 7 a + 14 Steven Bangirana-0786 404202 43

Multiplying Polynomials Example Multiply (3 x – 7 y)(7 x + 2 y) = (3 x)(7 x + 2 y) – 7 y(7 x + 2 y) = = 21 x 2 + 6 xy – 49 xy + 14 y 2 21 x 2 – 43 xy + 14 y 2 Steven Bangirana-0786 404202 44

Multiplying Polynomials Example Multiply (5 x – 2 z)2 = (5 x – 2 z) = (5 x)(5 x – 2 z) – 2 z(5 x – 2 z) = 25 x 2 – 10 xz + 4 z 2 = 25 x 2 – 20 xz + 4 z 2 Steven Bangirana-0786 404202 45

Multiplying Polynomials Example Multiply (2 x 2 + x – 1)(x 2 + 3 x + 4) = (2 x 2)(x 2 + 3 x + 4) + x(x 2 + 3 x + 4) – 1(x 2 + 3 x + 4) = 2 x 4 + 6 x 3 + 8 x 2 + x 3 + 3 x 2 + 4 x – x 2 – 3 x – 4 = 2 x 4 + 7 x 3 + 10 x 2 + x – 4 Steven Bangirana-0786 404202 46

Multiplying Polynomials You can also use a vertical format in arranging the polynomials to be multiplied. In this case, as each term of one polynomial is multiplied by a term of the other polynomial, the partial products are aligned so that like terms are together. This can make it easier to find and combine like terms. Steven Bangirana-0786 404202 47

Special Products

The FOIL Method When multiplying 2 binomials, the distributive property can be easily remembered as the FOIL method. F – product of First terms O – product of Outside terms I – product of Inside terms L – product of Last terms Steven Bangirana-0786 404202 49

Using the FOIL Method Example Multiply (y – 12)(y + 4) Product of First terms is y 2 (y – 12)(y + 4) Product of Outside terms is 4 y (y – 12)(y + 4) Product of Inside terms is -12 y (y – 12)(y + 4) Product of Last terms is -48 F O I L (y – 12)(y + 4) = y 2 + 4 y – 12 y – 48 = y 2 – 8 y – 48 Steven Bangirana-0786 404202 50

Using the FOIL Method Example Multiply (2 x – 4)(7 x + 5) L F F O I L (2 x – 4)(7 x + 5) = 2 x(7 x) + 2 x(5) – 4(7 x) – 4(5) I O = 14 x 2 + 10 x – 28 x – 20 = 14 x 2 – 18 x – 20 We multiplied these same two binomials together in the previous section, using a different technique, but arrived at the same product. Steven Bangirana-0786 404202 51

Special Products In the process of using the FOIL method on products of certain types of binomials, we see specific patterns that lead to special products. Squaring a Binomial (a + b)2 = a 2 + 2 ab + b 2 (a – b)2 = a 2 – 2 ab + b 2 Multiplying the Sum and Difference of Two Terms (a + b)(a – b) = a 2 – b 2 Steven Bangirana-0786 404202 52

Special Products Although you will arrive at the same results for the special products by using the techniques of this section or last section, memorizing these products can save you some time in multiplying polynomials. Steven Bangirana-0786 404202 53

Dividing Polynomials

Dividing Polynomials Dividing a polynomial by a monomial Divide each term of the polynomial separately by the monomial. Example Steven Bangirana-0786 404202 55

Dividing Polynomials Dividing a polynomial by a polynomial other than a monomial uses a “long division” technique that is similar to the process known as long division in dividing two numbers, which is reviewed on the next slide. Steven Bangirana-0786 404202 56

Dividing Polynomials Divide 43 into 72. Multiply 1 times 43. Subtract 43 from 72. Bring down 5. Divide 43 into 295. Multiply 6 times 43. Subtract 258 from 295. Bring down 6. Divide 43 into 376. Multiply 8 times 43. Subtract 344 from 376. Nothing to bring down. We then write our result as Steven Bangirana-0786 404202 57

Dividing Polynomials As you can see from the previous example, there is a pattern in the long division technique. Divide Multiply Subtract Bring down Then repeat these steps until you can’t bring down or divide any longer. We will incorporate this same repeated technique with dividing polynomials. Steven Bangirana-0786 404202 58

Dividing Polynomials Divide 7 x into 28 x 2. Multiply 4 x times 7 x+3. Subtract 28 x 2 + 12 x from 28 x 2 – 23 x. Bring down – 15. 35 x 15 Divide 7 x into – 35 x. Multiply – 5 times 7 x+3. Subtract – 35 x– 15 from – 35 x– 15. Nothing to bring down. So our answer is 4 x – 5. Steven Bangirana-0786 404202 59

Dividing Polynomials 2 x 10 2 2 x + 7 4 x 6 x + 8 2 4 x + 14 x 20 x + 8 20 x 70 78 Divide 2 x into 4 x 2. Multiply 2 x times 2 x+7. Subtract 4 x 2 + 14 x from 4 x 2 – 6 x. Bring down 8. Divide 2 x into – 20 x. Multiply -10 times 2 x+7. Subtract – 20 x– 70 from – 20 x+8. Nothing to bring down. 78 We write our final answer as 2 x 10 + ( 2 x + 7) Steven Bangirana-0786 404202 60
 6-2 rational exponents
6-2 rational exponents Lesson 5: negative exponents and the laws of exponents
Lesson 5: negative exponents and the laws of exponents Exponents and polynomials
Exponents and polynomials Polynomials in everyday life
Polynomials in everyday life Adding polynomial fractions
Adding polynomial fractions Dividing polynomials with exponents
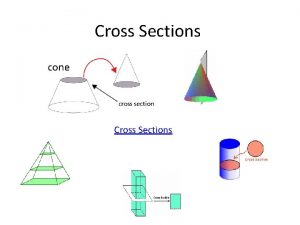
Dividing polynomials with exponents Cutaways and cross sections definition
Cutaways and cross sections definition Aristotle anatomy
Aristotle anatomy Dorsal side
Dorsal side Chapter 9 conic sections and analytic geometry
Chapter 9 conic sections and analytic geometry 11-1 space figures and cross sections
11-1 space figures and cross sections Health and safety at work act 1974 sections
Health and safety at work act 1974 sections Graduated commission example
Graduated commission example Traveling guideline hair cutting
Traveling guideline hair cutting Volumes of solids with known cross sections
Volumes of solids with known cross sections Body directional terms
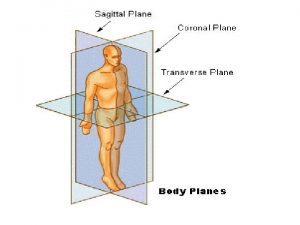
Body directional terms Body planes and sections
Body planes and sections Chapter 7 conic sections and parametric equations
Chapter 7 conic sections and parametric equations Chapter 9 conic sections and analytic geometry
Chapter 9 conic sections and analytic geometry Volumes of solids with known cross sections
Volumes of solids with known cross sections Declaration of independence sections
Declaration of independence sections Declaration of independence sections
Declaration of independence sections Chapter 5 lesson 4 declaring independence
Chapter 5 lesson 4 declaring independence Ctd sections
Ctd sections Venous drainage of stomach
Venous drainage of stomach Sections of solids engineering drawing
Sections of solids engineering drawing To find the true shape of the section
To find the true shape of the section Sectioned view
Sectioned view Pharynx parts
Pharynx parts Cobol sections
Cobol sections Pga sections map
Pga sections map Parabola in real life project
Parabola in real life project Method of sections
Method of sections Method of sections
Method of sections Rotating conic sections
Rotating conic sections Lesson 1 exploring conic sections
Lesson 1 exploring conic sections Volumes with known cross sections
Volumes with known cross sections Real-life applications of conic sections
Real-life applications of conic sections What is the yellow section of the erg
What is the yellow section of the erg Cross slice
Cross slice Diagonal cross section of a cube
Diagonal cross section of a cube Four conic sections
Four conic sections Types of conic sections
Types of conic sections Conic sections
Conic sections A perfect square trinomial
A perfect square trinomial Ctd sections
Ctd sections Conic sections graphing calculator
Conic sections graphing calculator Conic cheat sheet
Conic cheat sheet Conic sections equations
Conic sections equations Identify the conic x^2 y^2=16
Identify the conic x^2 y^2=16 Conic sections quiz
Conic sections quiz There are six logical units or sections to a computer
There are six logical units or sections to a computer Classifying conic sections worksheet answers
Classifying conic sections worksheet answers Vertices of a hyperbola formula
Vertices of a hyperbola formula Conic sections in polar coordinates
Conic sections in polar coordinates Units of mass moment of inertia are
Units of mass moment of inertia are Polar form of conic sections
Polar form of conic sections Conic sections
Conic sections Notebook with colored sections
Notebook with colored sections Is a cycloid a conic section
Is a cycloid a conic section Egypt is divided in how many sections
Egypt is divided in how many sections