Unit 5 Polynomials Exponents n Classification of Polynomials















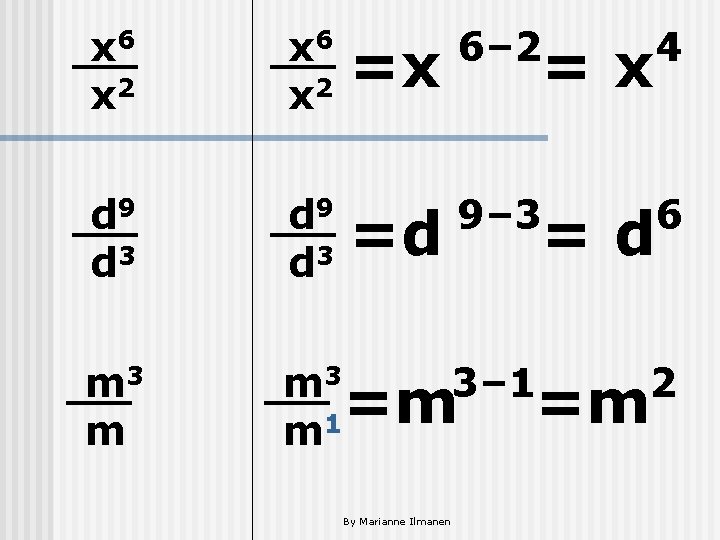



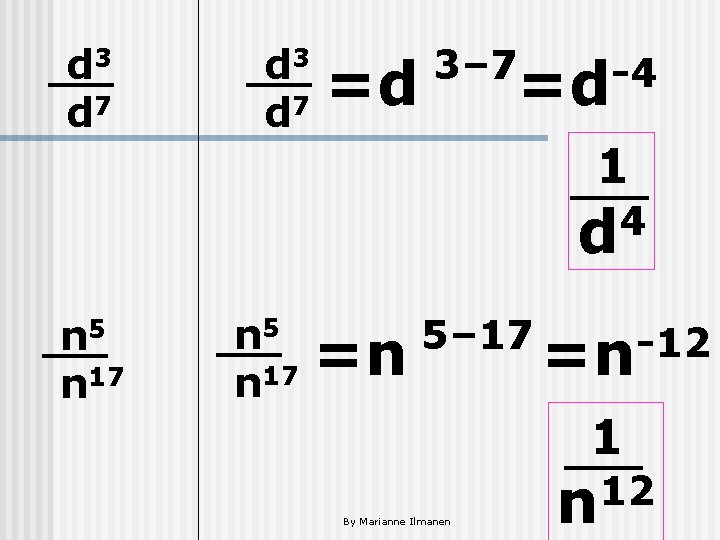


















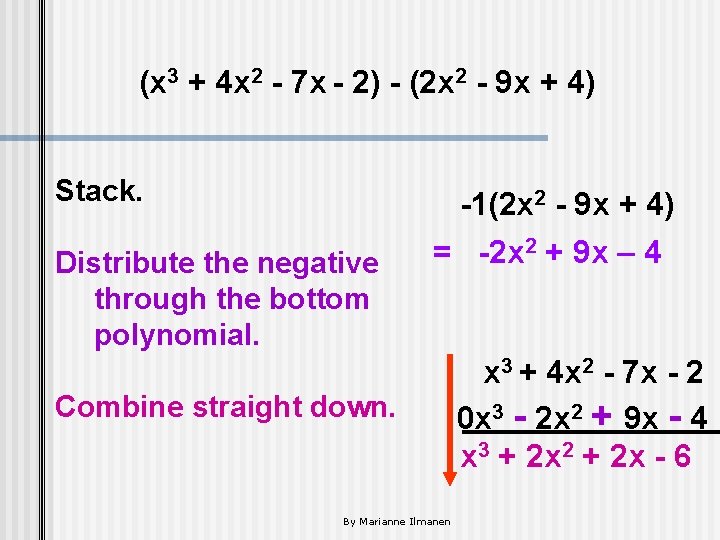



































- Slides: 85

Unit 5 Polynomials Exponents n Classification of Polynomials n Multiplying and Dividing Polynomials n Combining Polynomials n Special Products n By Marianne Ilmanen

Multiplying Monomials OBJECTIVE: Given five problems, the student will be able to multiply the monomials with 80% accuracy. Ca. SS 10. 0: Students add, subtract, multiply and divided monomials.

Check for Understanding n n n a 4 • a 7 a 4 b 2 c • a 2 b c 3 (7 x 4 y 7) (-3 x 2 y-2 ) (a 4 b c 3 )4 (3 m n 5 p 2)3 By Marianne Ilmanen

Rules for Multiplying Variables with Exponents n What do you do when Multiplying variables with exponents? n When multiplying, you multiply like variables within the expression. n When multiplying, you add the exponents. By Marianne Ilmanen

Rules for Multiplying Variables with Exponents 2 (a 3 b c)(a 2 b 5 c) 2 (a 3 b 2+1 =a = 3 a By Marianne Ilmanen c) (a 2 b 3+2 b 1+5 c 5 b 6 c 5 c)

Examples (3 3 x (-5 4 y 3 a )(-7 2 x b )( - a 5 y) 2 b) -21 3+2 x -21 5 x 5 3+1 a 5 4 a By Marianne Ilmanen 4+5 y 9 y 1+2 b 3 b

n What is the n When taking the power of a power, you multiply the exponents. rule for taking a power of a power? (a 2 b 3 c)(a 2 b 3 c) (a 2 b 3 c)4 a 2+2+2+2 b 3+3+3+3 c 1+1+1+1 8 a Shortcut… 12 b 4 c = (a 2 b 3 c)4 a 2 • 4 b 3 • 4 c 1 • 4 By Marianne Ilmanen = 8 a 12 b 4 c

Examples (3 x 3 y 4)3 3 4 3 4 (3 x y )(3 x y ) 1 • 3 3 • 3 4 • 3 3 x y 9 12 27 x y (2 3 b 2 4 c) 24 b 3 • 4 c 2 • 4 16 b 12 c 8 By Marianne Ilmanen

Find the Following Products: (3 g 7 h 3 j 2) (2 g 2 h 3 j) m 7(m 3 n 2) (xy)(yz)(xz) 3(ax 3 y)2 By Marianne Ilmanen

Find the Following Products: (3 g 7 h 3 j 2) (2 g 2 h 3 j) 6 g 9 h 6 j 3 m 7(m 3 n 2) m 10 n 2 (xy)(yz)(xz) x 2 y 2 z 2 3(ax 3 y)2 3 a 2 x 6 y 2 By Marianne Ilmanen

Check for Understanding n n n a 4 • a 7 n a 4 b 2 c • a 2 b c 3 n (7 x 4 y 7)(-3 x 2 y-2) n (a 4 b c 3)4 n (3 m n 5 p 2)3 n By Marianne Ilmanen a 11 a 6 b 3 c 4 -21 x 6 y 5 a 16 b 4 c 12 27 m 3 n 15 p 6

Summary Inspiration: What is the exponent rule for multiplying monomials? n How is the rule different for coefficients in the monomials? n What is the exponent rule for raising a monomial to another power? n How does this rule affect the coefficients in the monomial? n By Marianne Ilmanen

Dividing Monomials OBJECTIVE: Given four division problems, the student will be able to divide monomials with 75% accuracy. n Ca. SS 10. 0: Students add, subtract, multiply and divided monomials. n By Marianne Ilmanen

Check for Understanding x 11 3 x t 4 9 t 3 5 m n m 2 n 3 6 12 5 a b c a 6 b 2 c 7 By Marianne Ilmanen

What is the rule for dividing monomials? n If I add the exponents when I multiply monomials, then I will SUBTRACT need to _____ the exponents when I divide the monomials. By Marianne Ilmanen
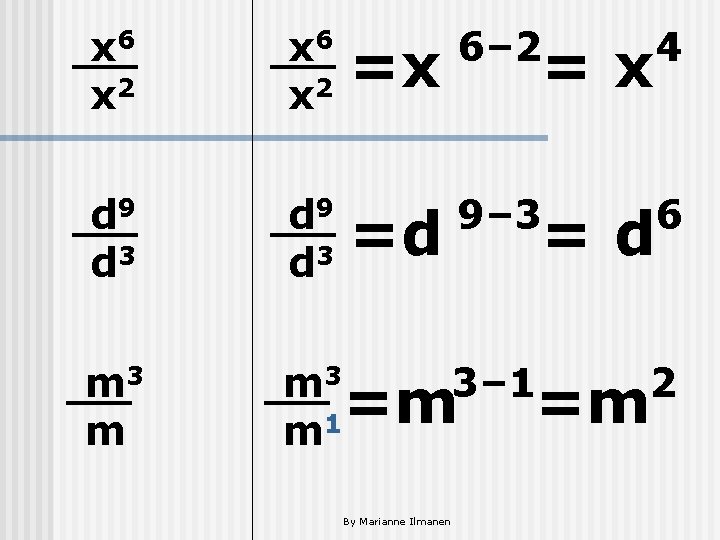
x 6 x 2 =x 6– 2 4 d 9 d 3 =d 9– 3 6 m 3 m m 3 3– 1 2 =m =m 1 m By Marianne Ilmanen =x =d

What happens when the exponent is the same in the numerator and denominator? 5 x 1 5 x =x 1 5– 5 =x Anything divided by itself equals one !!! Therefore, 0 x =1 Anything to the zero power equals one !!! By Marianne Ilmanen 0

x 3 y 4 = x 3 -2 y 4 -1 = x 1 y 3 2 2 x y xy 3 a 7 b 3 = a 7 -2 b 3 -3 = a 5 b 0 2 3 a b a 5 By Marianne Ilmanen

What happens when the exponent is negative? 2 x 5 x =x 2– 5 -3 =x x·x = x·x·x 1 1 1 x·x·x = 1 3 x So, a negative exponent means “put me on the other level…in this case, in the denominator. By Marianne Ilmanen
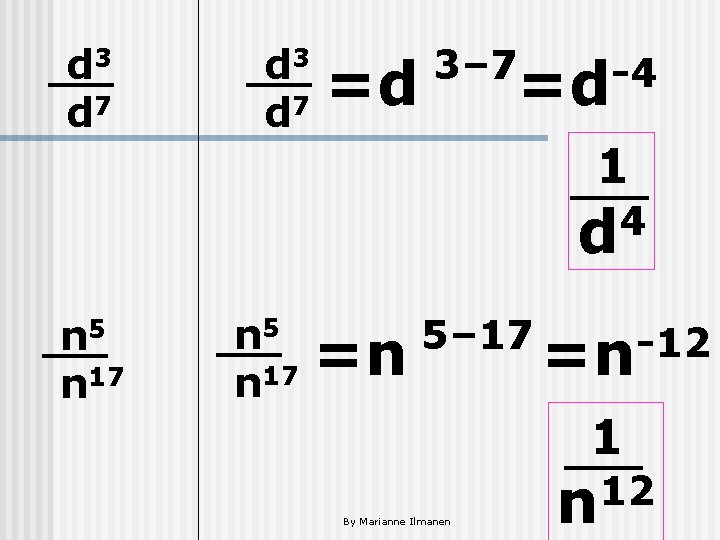
d 3 d 7 =d 3– 7 -4 =d 1 4 d n 5 n 17 =n 5– 17 -12 =n 1 By Marianne Ilmanen 12 n

m 6 n 2 p 8 11 2 7 m n p = m 6 -11 n 2 -2 p 8 -7 = -5 0 1 m n p By Marianne Ilmanen p 5 m

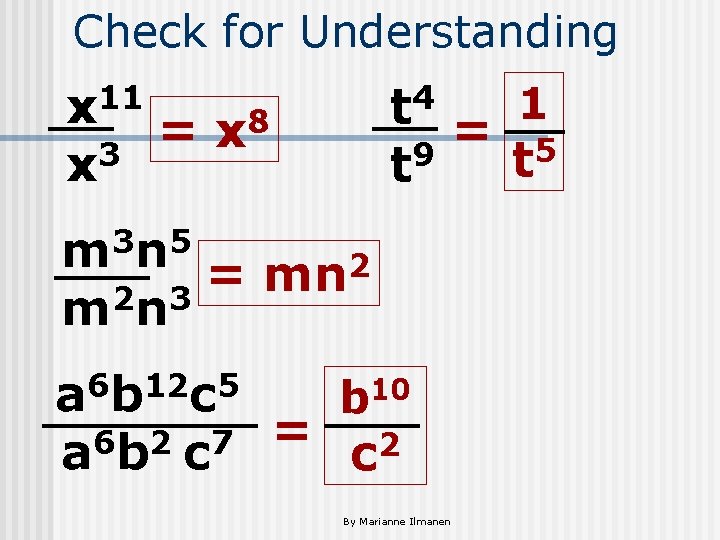
Check for Understanding x 11 = x 8 3 x t 4 = 1 5 9 t t m 3 n 5 = mn 2 2 3 m n a 6 b 12 c 5 b 10 = 6 2 7 2 a b c c By Marianne Ilmanen

Polynomial Terminology OBJECTIVE: Given two polynomials, the student will be able to find the degree and arrange the terms in descending order with 75% accuracy. Ca. SS 10. 0: Students add, subtract, multiply and divide polynomials.

Check for Understanding: Find the degree of each monomial in the polynomial term and arrange them in descending order with respect to X. abx 3 + bcx + 34 –x 7 7 x 3 + 5 yz - 3 xy 4 + x 4 yz – 13 x 2 z By Marianne Ilmanen

Types of Polynomials: n Monomial: n One or more numbers multiplied together n The sum of two monomials n The sum of three monomials 2 x 5 y n Binomial: 2 x 5 + 3 y n Trinomial: 2 x 5 + 3 y - 7 By Marianne Ilmanen

Degree of the Polynomial Degree: Monomial n The monomial of the n Tally up the highest degree is the exponents: Winner: n EXAMPLES: n EXAMPLE: 8 y 3 degree of 3 8 y 3 + 2 x - xy 4 + xy – 7 42 qrs degree of 3 4 y 4 ab degree of 6 3 rd 1 st 5 th 2 nd 0 th Degree Polynomial 5 -14 degree of 0 By Marianne Ilmanen

Find the Degree of the Polynomial 3 x – 5 First Degree -3 a 2 + 7 a – 19 Second Degree 14 x + x 2 y – 37 x 4 Fourth Degree – 7 a 2 b 2 + 5 a 2 b 3 - 4 ab 3 Fifth Degree By Marianne Ilmanen

Writing Polynomials in Descending Order n Write the terms so that the powers of y are in order from largest to smallest. 8 y 3 + 2 x - xy 4 + xy 2 – 7 y By Marianne Ilmanen

Writing Polynomials in Descending Order n Write the terms so that the powers of y are in order from largest to smallest. 8 y 3 + 2 x - xy 4 + xy 2 – 7 y 3 rd 0 4 th 2 nd 1 st - xy 4 + 8 y 3 + xy 2 – 7 y + 2 x By Marianne Ilmanen

Writing Polynomials in Descending Order n Write the terms so that the powers of a are in order from largest to smallest. 10 – a 2 b 3 + 7 ab – a 5 b 2 - 9 a 4 + b 3 0 2 nd 1 st 5 th 4 th 0 – a 5 b 2 - 9 a 4 – a 2 b 3 + 7 ab + b 3 + 10 By Marianne Ilmanen

Check for Understanding: Find the degree of the polynomial. Then arrange them in descending order with respect to X. abx 3 + bcx + 34 –x 7 Seventh Degree -x 7 + abx 3 + bcx + 34 7 x 3 + 5 yz - 3 xy 4 + x 4 yz – 13 x 2 z x 4 yz + 7 x 3 – 13 x 2 z - 3 xy 4 + 5 yz Sixth Degree By Marianne Ilmanen

Check for Understanding: Find the degree of the polynomial. Then arrange them in descending order with respect to X. 3 x 5 + 15 yz - 3 xy 4 + 7 x 4 yz 2 – 13 x 2 z 7 x 4 yz 2 + 3 x 5 – 13 x 2 z - 3 xy 4 + 15 yz Seventh Degree By Marianne Ilmanen

Adding and Subtracting Polynomials OBJECTIVE: Given four polynomial problems the student will be able to find the sum or difference with 75% accuracy.

Check for Understanding 1. (4 x 2 + 5 x) + (-7 x 2 + x) 2. (6 x 3 + 3 x 2 - 7) + (x 3 - 6 x 2 – 2 x) 3. (3 x 2 + 5 x - 6) - (7 x 2 - 9) 4. (5 b – 7 ab + 8 a) - (5 ab – 4 a) By Marianne Ilmanen

What are the steps to combining polynomials? 1. “Stack” the two polynomials and align the like terms. 2. Combine straight down. Remember: each term has variables that act as a “label” when you add, so the same “label” is carried into your answer. By Marianne Ilmanen

+ Find the sum of (3 + 2 a + a 2) and (5 - 8 a + a 2) 1. “Stack” the like terms. 2. Combine straight down. 3 + 2 a + a 2 5 - 8 a + a 2 8 – 6 a + 2 a 2 By Marianne Ilmanen

Let’s Try a Few: (3 x 4 + 2 x 3 + x 2) + (-5 x 4 + 8 x 3 + x 2) (5 x 2 – 4) + (3 x 2 + 8 x + 4) By Marianne Ilmanen

(3 x 4 + 2 x 3 + x 2)+(-5 x 4 + 8 x 3 + x 2) 3 x 4 + 2 x 3 + x 2 (+) -5 x 4 + 8 x 3 + x 2 -2 x 4 +10 x 3 +2 x 2 (5 x 2 -4)+(3 x 2 + 8 x + 4) 5 x 2 + 0 x - 4 (+) 3 x 2 + 8 x + 4 8 x 2 + 8 x + 0 8 x 2 + 8 x By Marianne Ilmanen

How do you find 1. Stack the two the difference of equations and align two polynomials? the like terms. 2. 3. Find the difference: (x 3 + 4 x 2 - 7 x - 2) - (2 x 2 - 9 x + 4) Distribute the negative through the bottom polynomial. Combine straight down. x 3 + 4 x 2 - 7 x - 2 (-) 0 x 3 + 2 x 2 - 9 x + 4 By Marianne Ilmanen
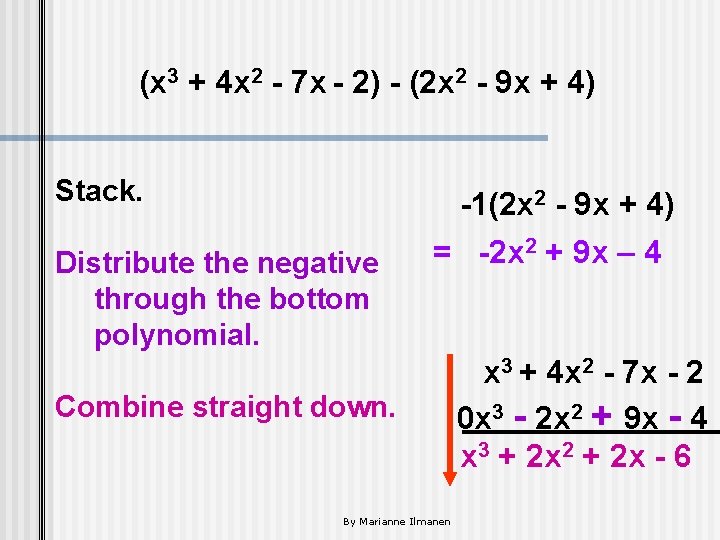
(x 3 + 4 x 2 - 7 x - 2) - (2 x 2 - 9 x + 4) Stack. Distribute the negative through the bottom polynomial. -1(2 x 2 - 9 x + 4) = -2 x 2 + 9 x – 4 Combine straight down. By Marianne Ilmanen x 3 + 4 x 2 - 7 x - 2 0 x 3 - 2 x 2 + 9 x - 4 x 3 + 2 x 2 + 2 x - 6

(4 x 3 + 8 x 2 - x + 21) - (3 x 2 - 10 x) Stack. -1(3 x 2 - 10 x) = -3 x 2 + 10 x Distribute. Combine straight down. 4 x 3 + 8 x 2 - x + 21 - 3 x 2 + 10 x 4 x 3 + 5 x 2 + 9 x +21 By Marianne Ilmanen

(3 x 2 y + xy – 5) - (2 x 2 y – 10 xy + 3) Stack. -1(2 x 2 y – 10 xy + 3) Distribute. = -2 x 2 y + 10 xy – 3 Combine straight down. By Marianne Ilmanen 3 x 2 y + xy – 5 -2 x 2 y + 10 xy – 3 1 x 2 y + 11 xy – 8

Check for Understanding 1. (4 x 2 + 5 x) + (-7 x 2 -3 x 2 + 6 x + x) 2. (6 x 3 + 3 x 2 – 7 x) + (x 3 - 6 x 2 – 2 x) 7 x 3 - 3 x 2 – 9 x 3. (3 x 2 + 5 x - 6) - (7 x 2 - 9) - 4 x 2 + 5 x + 3 4. (5 b – 7 ab + 8 a) - (5 ab – 4 a) By Marianne Ilmanen 5 b – 12 ab + 12 a

Summary Inspiration: n n What do you do when adding polynomials? What do you do when subtracting polynomials? What is the rule for combining things with exponents…how is the exponent affected or not affected? What do you do if you have two polynomials to add, but there is a monomial within one of the polynomials that does not have a like term in the other polynomial? By Marianne Ilmanen

Multiplying a Polynomial by a Monomial OBJECTIVE: Given three problems, the student will be able to find the product with 80% accuracy. Ca. SS 10. 0: Students add, subtract, multiply and divided polynomials.

Check for Understanding 1. 4 a 2 (-8 a 3 c + c -11) 2. -3 x (-8 xy - 5 y +4) + 2 (x 2 y -2 xy + x) 3. 5 w 2 (-8 w 3 + 2 w) + 2 w (w 4 – 5 w 2 -2) By Marianne Ilmanen

Use Distributive Property What property do I use when multiplying a polynomial by a monomial? n Distribute the monomial on the outside of the parentheses to each term of the polynomial inside the parentheses. Remember to add the exponents of the variables when multiplying!!!! By Marianne Ilmanen

Use Distributive Property n Distribute the monomial on the outside of the parentheses to each term of the polynomial inside the parentheses. 3 d (4 d 2 -8 d -15) 3 d(4 d 2) + 3 d(-8 d) + 3 d(-15) 12 d 3 -24 d 2 -45 d By Marianne Ilmanen

2 x 2 (5 x 2 -7 x +8) 2 x 2(5 x 2) + 2 x 2(-7 x) +2 x 2(8) 10 x 4 -14 x 3 + 16 x 2 3 gh (5 g 2 -8 gh +2 h) 3 gh(5 g 2) +3 gh(-8 gh) +3 gh(2 h) 15 g 3 h-24 g 2 h 2 +6 gh 2 By Marianne Ilmanen

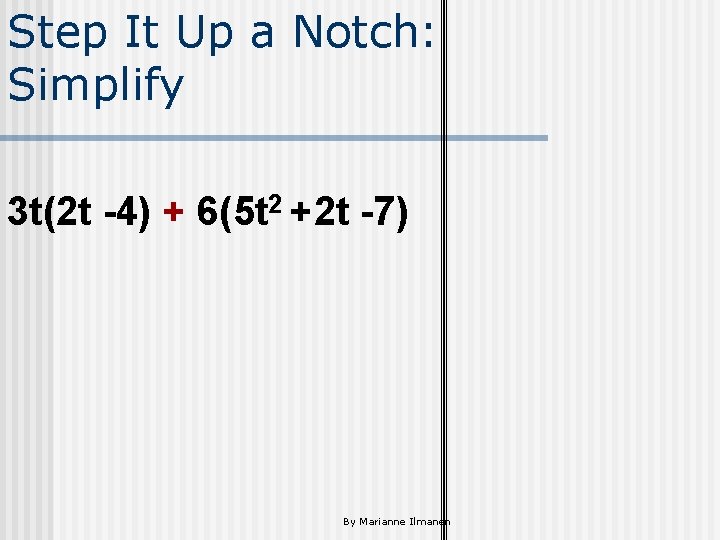
Step It Up a Notch: Simplify 3 t(2 t -4) + 6(5 t 2 +2 t -7) By Marianne Ilmanen

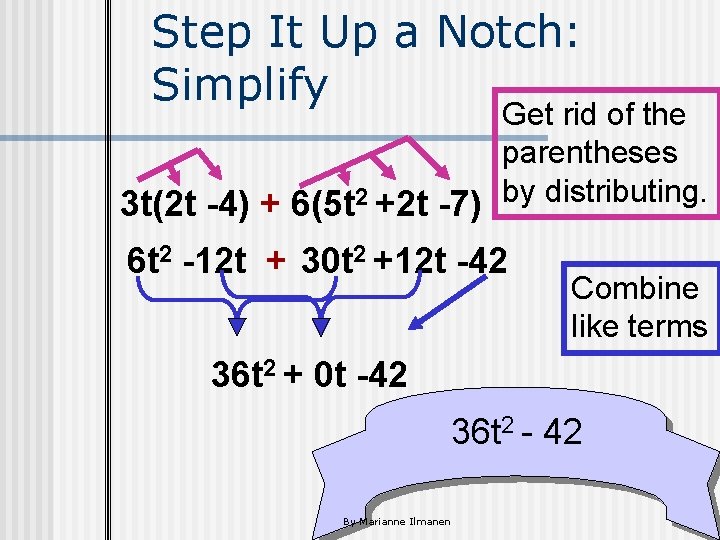
Step It Up a Notch: Simplify Get rid of the parentheses 3 t(2 t -4) + 6(5 t 2 +2 t -7) by distributing. 6 t 2 -12 t + 30 t 2 +12 t -42 Combine like terms 36 t 2 + 0 t -42 36 t 2 - 42 By Marianne Ilmanen

3(y 3 +8 y) + 4 y(2 y 3 -8 y 2 +2 y +9) By Marianne Ilmanen

Get rid of the parentheses by distributing. 3(y 3 +8 y) + 4 y(2 y 3 -8 y 2 +2 y +9) 3 y 3 +24 y + 8 y 4 -32 y 3 +8 y 2 +36 y By Marianne Ilmanen

Get rid of the parentheses by distributing. 3(y 3 +8 y) + 4 y(2 y 3 -8 y 2 +2 y +9) 3 y 3 +24 y + 8 y 4 -32 y 3 +8 y 2 +36 y 8 y 4 -29 y 3 +8 y 2 + 60 y By Marianne Ilmanen Combine like terms

Check for Understanding 1. 4 a 2 (-8 a 3 c + c -11) -32 a 5 c + 4 a 2 c -44 a 2 2. -3 x (-8 xy - 5 y +4) + 2 (x 2 y -2 xy + x) 24 x 2 y +15 xy -12 x + 2 x 2 y -4 xy + 2 x 26 x 2 y +11 xy -10 x 3. 5 w 2 (-8 w 3 + 2 w) + 2 w (w 4 – 5 w 2 -2) -40 w 5 + 10 w 3 + 2 w 5 – 10 w 3 - 4 w -38 w 5 - 4 w By Marianne Ilmanen

Summary Inspiration: What property is used when multiplying a polynomial by a monomial? n What do you do when multiplying the coefficients? n What do you do when multiplying the variables? n What is the last step if you have any like terms? n By Marianne Ilmanen

Multiplying Polynomials OBJECTIVE: Given 4 multiplication problems, the student will be able to find the product with 75% accuracy. Ca. SS 10. 0: Students add, subtract, multiply and divided polynomials.

Check for Understanding 1. (y – 7) (y + 3) 2. (2 m + 5) (3 m - 8) 3. (3 p – 7) (3 p + 7) 4. (0. 5 y – 7) (0. 4 y + 3) By Marianne Ilmanen

What is the result of multiplying two binomials? n When multiplying two binomials, the result is a binomial, four termed polynomial or (most commonly) a trinomial. (x – 7) (x + 3) x 2 – 4 x - 21 By Marianne Ilmanen

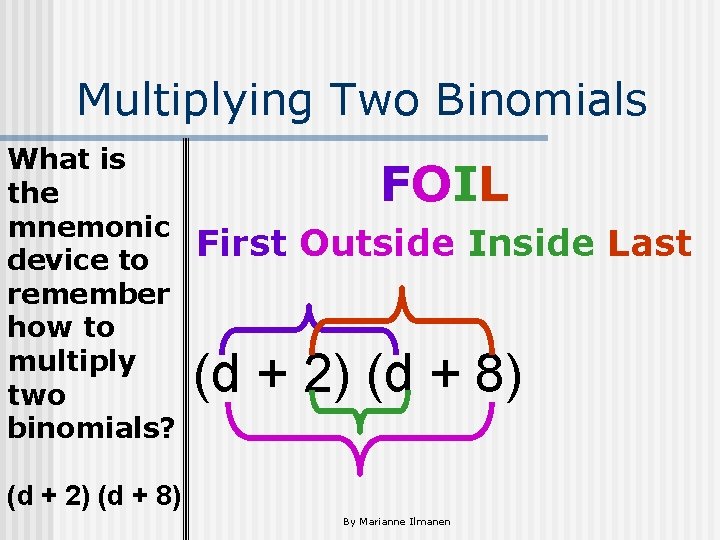
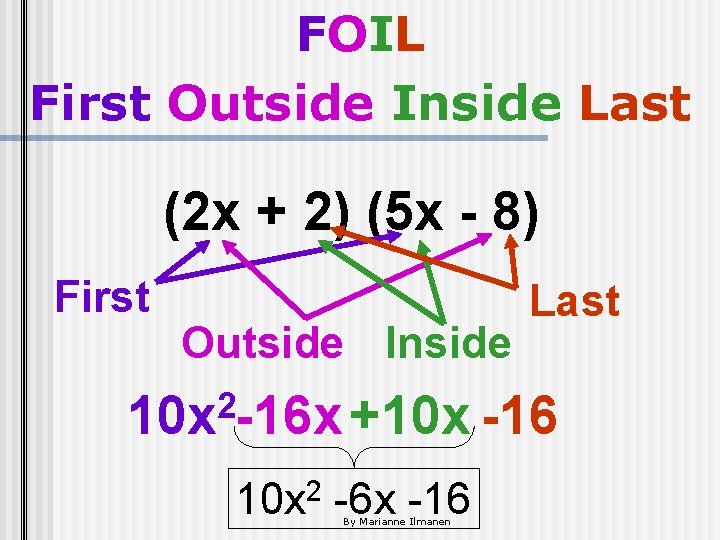
Multiplying Two Binomials What is the mnemonic device to remember how to multiply two binomials? FOIL First Outside Inside Last (d + 2) (d + 8) By Marianne Ilmanen

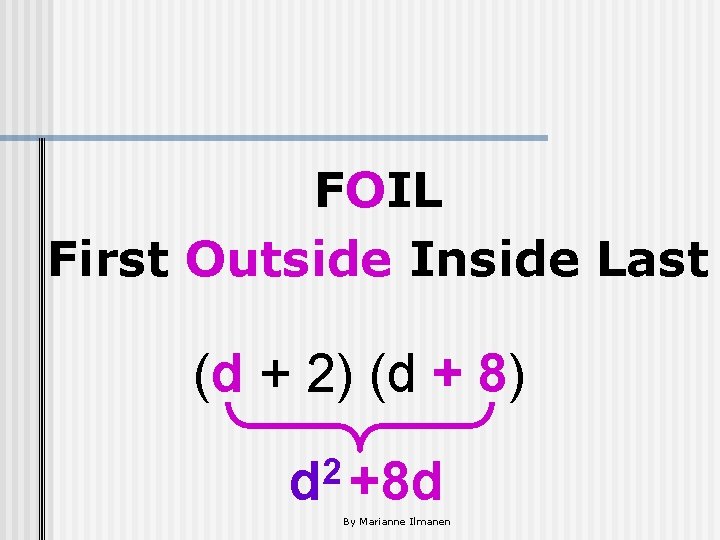
Multiplying Two Binomials: FOIL First Outside Inside Last (d + 2) (d + 8) 2 d By Marianne Ilmanen

FOIL First Outside Inside Last (d + 2) (d + 8) 2 d +8 d By Marianne Ilmanen

FOIL First Outside Inside Last (d + 2) (d + 8) 2 d +8 d +2 d By Marianne Ilmanen

FOIL First Outside Inside Last (d + 2) (d + 8) 2 d +8 d +2 d +16 By Marianne Ilmanen

Combine the Middle Terms 2 d +8 d +2 d +16 2 d +10 d +16 By Marianne Ilmanen

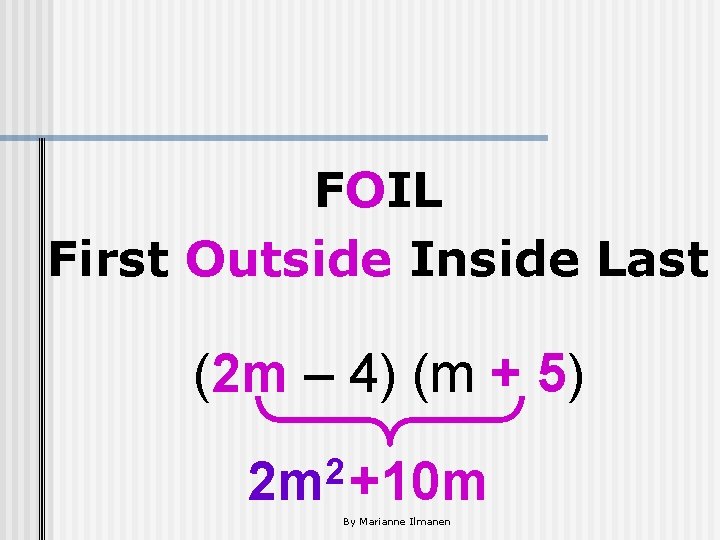
Multiply: (2 m – 4) (m + 5) FOIL First Outside Inside Last (2 m – 4) (m + 5) By Marianne Ilmanen

Multiplying Two Binomials: FOIL First Outside Inside Last (2 m – 4) (m + 5) 2 2 m By Marianne Ilmanen

FOIL First Outside Inside Last (2 m – 4) (m + 5) 2 2 m +10 m By Marianne Ilmanen

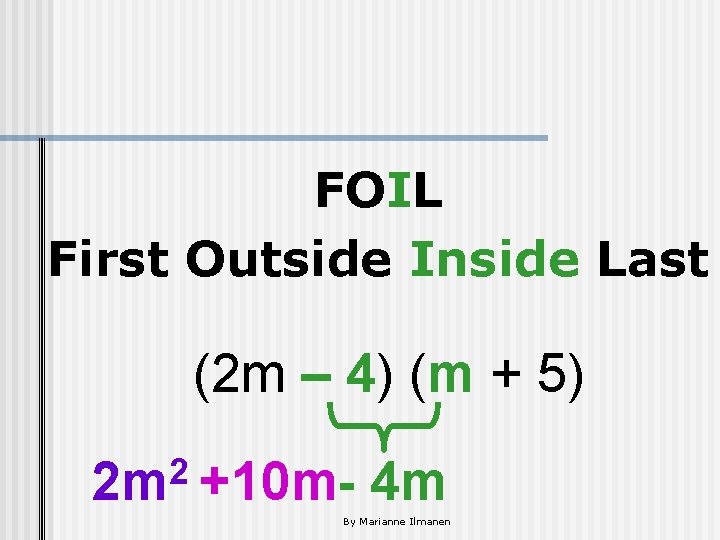
FOIL First Outside Inside Last (2 m – 4) (m + 5) 2 2 m +10 m- 4 m By Marianne Ilmanen

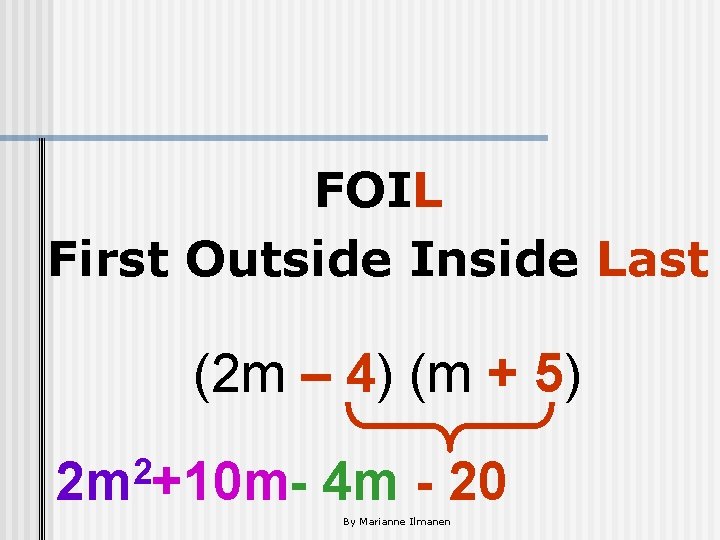
FOIL First Outside Inside Last (2 m – 4) (m + 5) 2 2 m +10 m- 4 m - 20 By Marianne Ilmanen

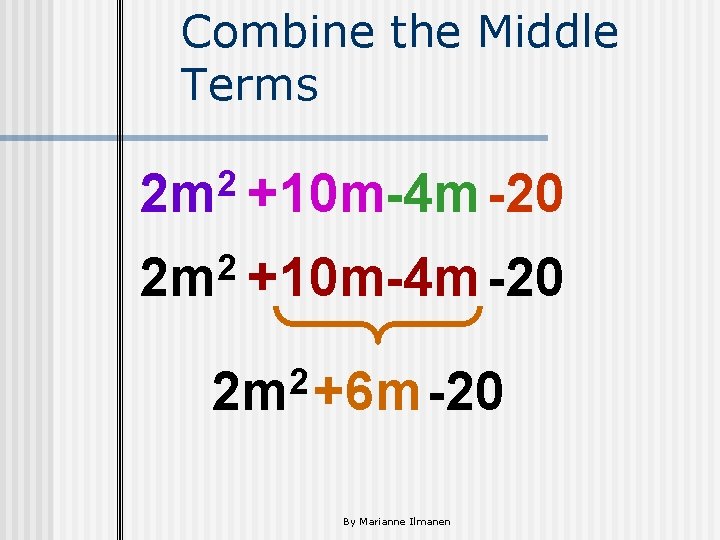
Combine the Middle Terms 2 2 m +10 m-4 m -20 2 2 m +6 m -20 By Marianne Ilmanen

Multiply: (2 x + 2) (5 x - 8) FOIL First Outside Inside Last (2 x + 2) (5 x - 8) By Marianne Ilmanen

FOIL First Outside Inside Last (2 x + 2) (5 x - 8) First Outside Inside Last 2 10 x -16 x +10 x -16 10 x 2 -6 x -16 By Marianne Ilmanen

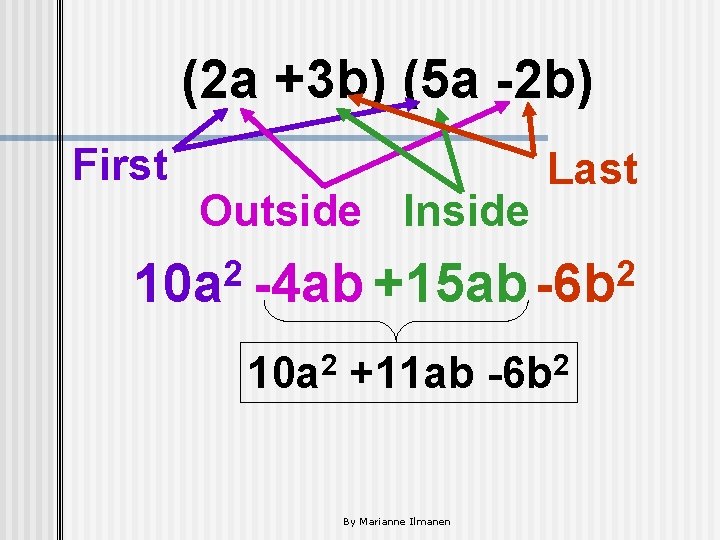
(2 a +3 b) (5 a -2 b) First Outside Inside Last 2 2 10 a -4 ab +15 ab -6 b 2 10 a +11 ab By Marianne Ilmanen 2 -6 b

Check for Understanding 1. (y – 7) (y + 3) y 2 – 4 y - 21 2 – m - 40 6 m 2. (2 m + 5) (3 m - 8) 3. (3 p – 7) (3 p + 7) 9 p 2 - 49 4. (5 y – 7 z) (4 y + 3 z) 20 y 2 – 13 yz – 21 z 2 By Marianne Ilmanen

Special Products OBJECTIVE: Same as 9 -7.

What is a difference of squares and how is it different than the other trinomial products we have talked about? n A difference (SUBTRACTION) of (PERFECT) squares is exactly that…the result (ANSWER) will be two perfect squares, one subtracted from the other. By Marianne Ilmanen

n A difference (SUBTRACTION) of (PERFECT) squares is exactly that…the result (ANSWER) will be two perfect squares, one subtracted from the other. (g + 8) (g - 8) FOIL it out… g 2 +0 g – 64 2 g – 64 It is different because the “OI” terms are additive inverses so they “zero out. ” There is no first degree term in a difference of squares. By Marianne Ilmanen

Difference of Squares: Example (3 g + 4) (3 g - 4) By Marianne Ilmanen

Difference of Squares (3 g + 4) (3 g - 4) 2 9 g +12 g – 12 g -16 0 9 g 2 – 16 By Marianne Ilmanen FL

(3 x + 5) (3 x - 5) 9 x 2 + 15 x – 25 9 x 2 - 25 (9 – z 9) (9 + z 9) 81 - 9 z 9 + 9 z 9 – z 18 81 – z 18 (5 b – 12 a) (5 b + 12 a) 25 b 2 - 60 ab + 60 ab – 144 a 2 25 b 2 – 144 a 2 (½x + ½y) (½x - ½y) ¼ x 2 + ¼xy – ¼ y 2 By Marianne Ilmanen ¼ x 2 – ¼ y 2

Why can I distribute the power to a monomial, but not a binomial? (4 xy)2 (4 xy) (42 x 2 y 2) (16 x 2 y 2) No FOIL (4 x + y)2 (4 x + y) 16 x 2+4 xy+y 2 16 x 2+8 xy+y 2 By Marianne Ilmanen FOIL

Perfect Squares (3 x – 2 6) (3 x – 6)2 = (3 x – 6) 9 x 2 – 18 x +36 -36 x 9 x 2 – 36 x + 36 (2 x + 5 y)2=(2 x + 5 y) 4 x 2 +10 x +25 y 2 By Marianne Ilmanen -36 x 9 x 2 – 36 x + 36

Perfect Squares (3 x + 6 y)2= (3 x +6 y) 9 x 2+18 xy+36 +36 xy 9 x 2 +36 xy + 36 (5 a – 12 b)2 (5 a– 12 b)2= (5 a – 12 b) 25 a 2 -60 ab– 60 ab +144 b 2 -120 ab 25 a 2 – 120 ab + 144 b 2 By Marianne Ilmanen

Summary Inspiration: n n What does FOIL stand for? Show the steps on the binomial product below. (a + b) (c + d) Which terms do you usually combine after FOIL-ing? What is special about Differences of Squares? What is special about Perfect Squares? By Marianne Ilmanen