esimerkki 19 esimerkki 1 Perkrryyn lastataan tiiliskivi jotka

esimerkki 19 esimerkki 1 Peräkärryyn lastataan tiiliskiviä, jotka painavat 6 kg/kpl. Auton peräkärryn oma massa on 170 kg. Kuinka paljon on kärryn kokonaismassa, jos kärryyn on lastattu tiiliskiviä a) 10 kpl, b) 20 kpl, c) 50 kpl, d) x kpl? ratkaisu esimerkki 1 Tiiliskivet (kpl) x Kokonaismassa (kg) y 10 6 · 10 + 170 = 230 20 6 · 20 + 170 = 290 50 6 · 50 + 170 = 470 x 6 · x + 170 Lineaarinen riippuvuus Merkitään tiiliskivien määrää x: llä ja kärryn kokonaismassaa y: llä. Lasketaan kokonaismassa annetuilla tiiliskivien määrillä.

Kun tiiliskiviä on lastattu kärryyn x kpl, niiden kokonaismassa on 6 x. Lisätään tähän vielä kärryn oma paino, jolloin kärryn kokonaismassaksi y voidaan kirjoittaa lauseke 6 x + 170. vastaus: a) 230 kg, b) 290 kg, c) 470 kg, d) (6 x + 170) kg. Lineaarinen riippuvuus

esimerkki 20 esimerkki 1 Peräkärryyn lastataan tiiliskiviä, jotka painavat 6 kg/kpl. Auton peräkärryn oma paino on 170 kg. Peräkärryn kokonaismassan y ja tiiliskivien määrän x välistä yhteyttä kuvaa yhtälö y = 6 x + 170. Havainnollista yhteyttä kuvaajalla. ratkaisu esimerkki 1. Yhtälön muodosta havaitaan, että kuvaaja on suora. Suoran piirtämiseksi lasketaan kolme pistettä, joiden kautta suora voidaan piirtää. Tiiliskivet (kpl) x Kokonaismassa (kg) y 10 6 · 10 + 170 = 230 20 6 · 20 + 170 = 290 50 6 · 50 + 170 = 470 x 6 · x + 170 Lineaarinen riippuvuus

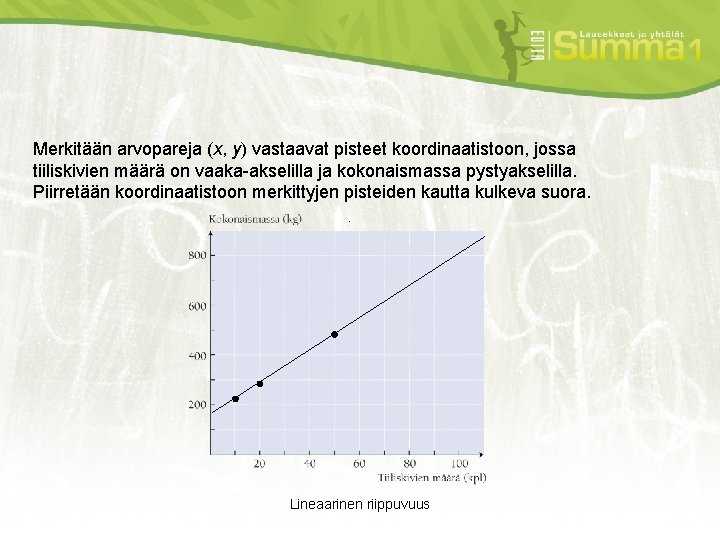
Merkitään arvopareja (x, y) vastaavat pisteet koordinaatistoon, jossa tiiliskivien määrä on vaaka-akselilla ja kokonaismassa pystyakselilla. Piirretään koordinaatistoon merkittyjen pisteiden kautta kulkeva suora. . Lineaarinen riippuvuus

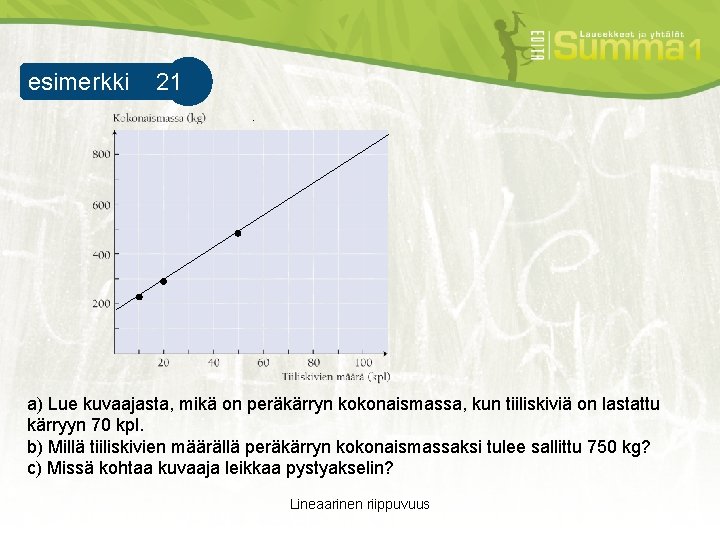
esimerkki 21 esimerkki 1. a) Lue kuvaajasta, mikä on peräkärryn kokonaismassa, kun tiiliskiviä on lastattu kärryyn 70 kpl. b) Millä tiiliskivien määrällä peräkärryn kokonaismassaksi tulee sallittu 750 kg? c) Missä kohtaa kuvaaja leikkaa pystyakselin? Lineaarinen riippuvuus

ratkaisu esimerkki 1. a) Kun tiiliskiviä on lastattu kärryyn 70 kpl, kärryn kokonaismassa on hieman alle 600 kg. b) Kokonaismassaksi tulee sallittu 750 kg, kun tiiliskiviä on kärryssä noin 96 kpl. c) Kuvaaja leikkaa pystyakselin kohdassa y = 170, joka vastaa kärryn omaa massaa. Lineaarinen riippuvuus

Funktio Kun y: n arvo on riippuvainen x: n arvosta, sanotaan, että y on x: n funktio. Tällöin käytetään merkintää y = f(x). Funktio on sääntö, jonka mukaan y: n arvo saadaan laskettua x: n arvon perusteella. Lineaarisen funktion kuvaama sääntö on aina muotoa f(x) = kx + b, missä k ja b ovat lukuja. Lineaarisen funktion kuvaaja on suora. Lineaarinen riippuvuus

esimerkki 22 esimerkki 1 y = f(x), missä f(x) = 2 x – 5. a) Mikä on x: n ja y: n välistä riippuvuutta kuvaavan funktion nimi. b) Mikä on funktion f lauseke? c) Minkä arvon funktio antaa y: lle, kun x saa arvon 4? d) Millä x: n arvolla y: n arvoksi tulee 75? ratkaisu esimerkki 1 a) Funktion nimi on f. b) Funktion lauseke on 2 x – 5. c) f(4) = 2 ∙ 4 – 5 = 3 d) 2 x – 5 = 75, kun x: n arvo on 40. y saa arvon 3, kun x: n arvo on 4. y saa arvon 75, kun x: n arvo on 40. Lineaarinen riippuvuus

esimerkki 22 esimerkki 1 Laske funktion f(x) = 4 x + 6 arvo, kun x saa arvot a) 3, b) , c) – 3. ratkaisu esimerkki 1 a) f(3) = 4 ∙ 3 + 6 = 18 b) c) f(– 3) = 4 ∙ (– 3) + 6 = – 12 + 6 = – 6 Lineaarinen riippuvuus

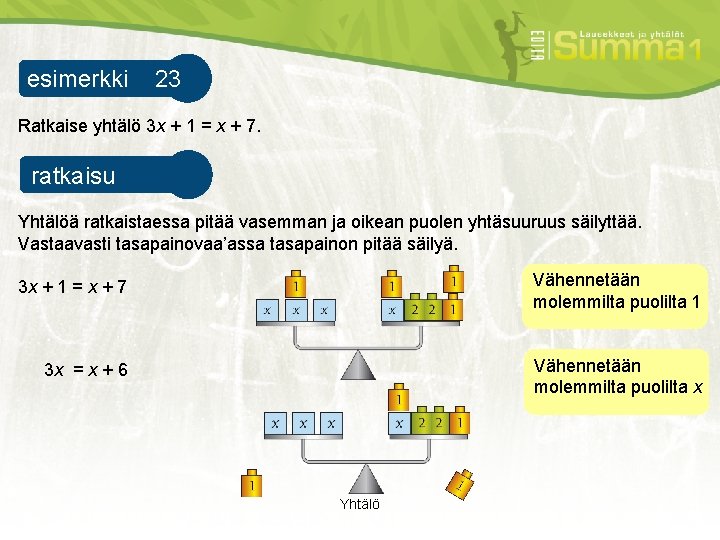
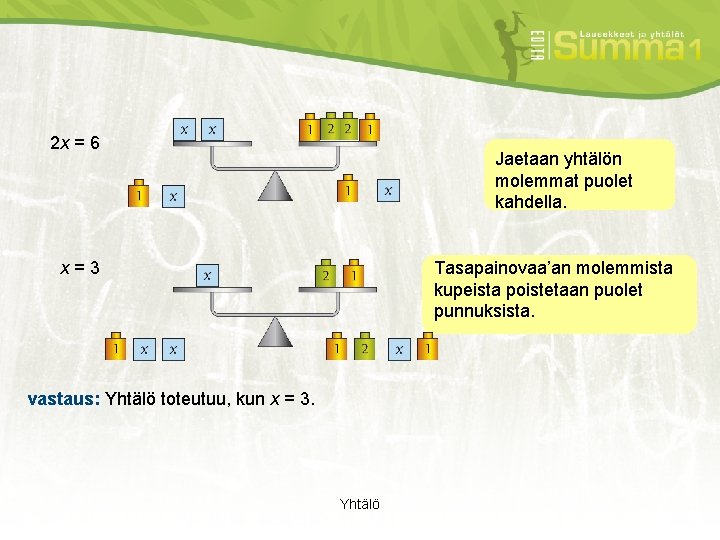
esimerkki 23 esimerkki 1 Ratkaise yhtälö 3 x + 1 = x + 7. ratkaisu esimerkki 1 Yhtälöä ratkaistaessa pitää vasemman ja oikean puolen yhtäsuuruus säilyttää. Vastaavasti tasapainovaa’assa tasapainon pitää säilyä. 3 x + 1 = x + 7 Vähennetään molemmilta puolilta 1 3 x = x + 6 Vähennetään molemmilta puolilta x Yhtälö

2 x = 6 Jaetaan yhtälön molemmat puolet kahdella. x = 3 Tasapainovaa’an molemmista kupeista poistetaan puolet punnuksista. vastaus: Yhtälö toteutuu, kun x = 3. Yhtälö

esimerkki 24 esimerkki 1 Ratkaise yhtälö. a) b) c) ratkaisu a) esimerkki 1 Vähennetään molemmilta puolilta 5. Vähennetään molemmilta puolilta 6 x. Jaetaan molemmat puolet luvulla – 4. Tarkistetaan ratkaisun oikeellisuus sijoittamalla saatu ratkaisu alkuperäiseen yhtälöön. Vasen puoli: Oikea puoli: Yhtälön ratkaisu x = – 3 toteuttaa yhtälön. Yhtälö

ratkaisu b) esimerkki 1 Kerrotaan molemmat puolet luvulla 3. Lisätään molemmille puolille 9. Vähennetään molemmilta puolilta x. Jaetaan molemmat puolet luvulla 2. Tarkistetaan ratkaisun oikeellisuus sijoittamalla saatu ratkaisu alkuperäiseen yhtälöön. Vasen puoli: Oikea puoli: Yhtälön ratkaisu x = 12 toteuttaa yhtälön. Yhtälö

ratkaisu c) esimerkki 1 Kerrotaan molemmat puolet luvulla 10. Supistetaan jakajat pois. Poistetaan sulkeet kertomalla. Vähennetään molemmilta puolilta 15. Vähennetään molemmilta puolilta 2 x. Jaetaan molemmat puolet luvulla 3. Yhtälö

Tarkistetaan ratkaisun oikeellisuus sijoittamalla saatu ratkaisu alkuperäiseen yhtälöön. Vasen puoli: Oikea puoli: Yhtälön ratkaisu toteuttaa yhtälön. Yhtälö

esimerkki 25 esimerkki 1 Ratkaise yhtälö. a) b) ratkaisu a) esimerkki 1 Kerrotaan sulkeet pois. Vähennetään molemmilta puolilta 3. Vähennetään molemmilta puolilta 2 x. Yhtälö on epätosi x: n arvosta riippumatta, joten yhtälöllä ei ole ratkaisua. vastaus: Yhtälöllä ei ole ratkaisua. Yhtälö

ratkaisu b) esimerkki 1 Kerrotaan sulkeet pois. Vähennetään molemmilta puolilta x. Yhtälö on tosi x: n arvosta riippumatta, joten kaikki luvut toteuttavat yhtälön. vastaus: Kaikki x: n arvot toteuttavat yhtälön. Yhtälö

esimerkki 26 esimerkki 1 Osakkeen arvo nousi vuodessa 23 %. Mikä oli osakkeen arvo vuosi sitten, kun sen arvo vuoden kuluttua oli 73, 80 €? ratkaisu esimerkki 1 Osakkeen kohonnut arvo on 100 % + 23 % = 123 % vuoden takaisesta arvosta. Merkitään kysyttyä arvoa x: llä, jolloin saadaan yhtälö Ratkaistaan yhtälö. vastaus: Osakkeen arvo oli vuosi sitten 60 €. Ongelmasta yhtälöksi

esimerkki 27 esimerkki 1 Sisun perheen asunnossa tapahtui vesivahinko. Sisun perheen kotivakuutuksessa oli 500 €: n omavastuu. Vakuutusyhtiön maksama korvaus oli 70 % siitä kustannusten määrästä, joka ylitti omavastuun. Kuinka suuret olivat vesivahingosta aiheutuneet kustannukset yhteensä, kun Sisun perheen osuudeksi kustannuksista jäi 2 570 €? ratkaisu esimerkki 1 Ratkaistava suure on vahingosta aiheutuneet kustannukset. Merkitään x: llä kustannusten kokonaismäärää, jonka avulla voidaan ilmoittaa vakuutusyhtiön maksama korvaus. Kustannukset yhteensä Omavastuun ylittävä kustannus Vakuutusyhtiön maksama korvaus Sisun perheen maksama osuus x 500 x – 500 0, 7(x – 500) 2 570 Ongelmasta yhtälöksi

Kun kustannusten määrästä vähennetään vakuutusyhtiön maksama korvaus, saadaan Sisun perheen maksettavaksi jäänyt osuus. Näin saadaan yhtälö, jos kustannusten kokonaismäärä voidaan ratkaista. vastaus: Kustannusten kokonaismäärä oli 7 400 €. Ongelmasta yhtälöksi

esimerkki 28 esimerkki 1 Suorakulmion lyhyemmän sivun pituuden pitää olla 60 % pidemmän sivun pituudesta. Määritä sivujen pituudet, kun suorakulmion piirin pituus on 4, 8 m. ratkaisu esimerkki 1 Merkitään pidemmän sivun pituutta x: llä, jolloin lyhyemmän sivun pituus on 0, 6 x. x 0, 6 x x Suorakulmion piirin pituus voidaan ilmoittaa sekä sivujen pituuksien summana että tunnettuna metrimääränä. Näin saadaan yhtälö, josta ratkaistaan x: n arvo. Ongelmasta yhtälöksi

Pidemmän sivun pituus, jota merkittiin x: llä, on 1, 5 m. Lyhyemmän sivun pituus on 0, 6 ∙ 1, 5 m = 0, 9 m. Ratkaisun oikeellisuudesta voidaan olla varmoja, koska piirin pituudeksi saadaan 1, 5 m + 0, 9 m = 4, 8 m, joka on yhtä suuri kuin tehtävässä annettu piiri. vastaus: Suorakulmion sivujen pituudet ovat 0, 9 m ja 1, 5 m. Ongelmasta yhtälöksi

esimerkki 29 esimerkki 1 Juu Pyry ja Pii haluavat leipoa juustosarvia 70 kpl. Reseptissä 50 stosarvet (16 g kp aineiden määrät on mitoitettu 16 juustosarven mukaan. marga l) 3 dl r vehnä iinia 2 dl Muunna reseptin aineiden määrät siten, että ne jauhoj a k e 2 dl rmavii riittävät 70 juustosarven leipomiseen. liä 2 tl ratkaisu esimerkki 1 Reseptin eri aineiden määrät muutetaan suuremmaksi samassa suhteessa kuin leivottavien juustosarvien määrää lisätään 16 kappaleesta 70 kappaleeseen. Aineiden määriä lisätään siis suhteessa 70 : 16. Suhde ja verranto juusto ra leivinj astetta auhett a

Rasvaa · 50 g = 218, 75 g ≈ 220 g Vehnäjauhoja · 3 dl = 13, 125 dl ≈ 13 dl Kermaviiliä · 2 dl = 8, 75 dl ≈ 9 dl Juustoraastetta · 2 dl = 8, 75 dl ≈ 9 dl Leivinjauhetta · 2 tl = 8, 75 tl ≈ 9 tl vastaus: Leivottaessa 70 kpl juustosarvia tarvitaan 220 g rasvaa, 13 dl vehnäjauhoja, 9 dl kermaviiliä, 9 dl juustoraastetta ja 9 teelusikallista leivinjauhetta. Suhde ja verranto

esimerkki 30 esimerkki 1 Sisu ja Kara ottivat yhteisen taksikyydin, jonka hinnaksi tuli 50, 40 €. Kustannus päätettiin jakaa matkojen pituuksien suhteessa. Sisu jäi kyydistä 15 kilometrin jälkeen, minkä jälkeen Kara matkusti yksin vielä 6 km. Laske Sisun ja Karan osuudet taksikyydin hinnasta. ratkaisu esimerkki 1 Merkitään kilometriä kohti muodostunutta kustannusta x: llä. Tällöin Sisun osuus on 15 x ja Karan osuus 21 x, joista saadaan yhtälö 15 x + 21 x = 50, 40. Ratkaisemalla saadaan Suhde ja verranto

Sisun osuus taksimaksusta on 15 x eli 15 · 1, 40 € = 21 €. Karan osuus on 21 x eli 21 · 1, 40 € = 29, 40 €. Karan osuus voidaan laskea myös erotuksena 50, 40 € � 21 € = 29, 40 €. vastaus: Sisun osuus 21 € ja Karan osuus 29, 40 €. Suhde ja verranto

esimerkki 31 esimerkki 1 Ratkaise verrannot. a) b) ratkaisu a) esimerkki 1 Ratkaistaan verranto ristiin kertomalla. Suhde ja verranto

ratkaisu b) esimerkki 1 Ratkaistaan verranto ristiin kertomalla. Suhde ja verranto

esimerkki 32 esimerkki 1 Sisu pyöräili keskinopeudella 20 km/h lenkin, jonka pituus oli 26 km. Kuinka pitkän lenkin hän olisi samassa ajassa pyöräillyt, mikäli keskinopeus olisi ollut 4 km/h suurempi? ratkaisu esimerkki 1 Kerätään tiedot taulukkoon: Nopeus (km/h) Matka (km) 20 26 24 x Verrannollisuus

Kun aika on vakio, nopeus ja matka ovat keskenään suoraan verrannollisia suureita. Jos nopeutta nostetaan, matkan pituus pitenee. Ratkaistaan kysytty matka verrannon avulla. (km) vastaus: Pyörälenkin pituus olisi ollut 31 km. Verrannollisuus

esimerkki 33 esimerkki 1 Kara leipoo mokkapaloja, joiden leivontaohjeessa on vehnäjauhojen määräksi annettu 250 g ja sokerin määräksi 150 g. Karalla ei ole kuitenkaan käytössä talousvaakaa, vaan hän mittaa aineet desilitroina. Kara löytää netistä tiedon, että 1 dl jauhoja painaa 65 g ja 1 dl sokeri painaa 85 g. Kuinka paljon Kara mittaa desilitroina a) jauhoja, b) sokeria? ratkaisu a) esimerkki 1 Vehnäjauhojen määristä saadaan taulukko. . Jauhoja (g) Jauhoja (dl) 250 x 65 1 Verrannollisuus

Saman aineen määrä grammoina ja desilitroina ovat suoraan verrannolliset. Jauhojen määrä desilitroina voidaan ratkaista verrannon avulla. vastaus: Mokkapaloihin laitetaan jauhoja 4 dl. Verrannollisuus

ratkaisu b) esimerkki 1 Sokerin määristä saadaan taulukko. Sokeria (g) Sokeria (dl) 150 x 85 1 Kuten jauhojen määrä, myös sokerin määrä desilitroina voidaan ratkaista verrannon avulla. vastaus: Mokkapaloihin laitetaan sokeria Verrannollisuus dl.

esimerkki 34 esimerkki 1 Kara osti torilta 1, 5 kg omenoita, joiden kilohinta oli 1, 90 €. Supermarketissa sai omenoita hintaan 1, 20 €/kg. Kuinka paljon Kara olisi saanut omenoita samalla rahamäärällä supermarketista? ratkaisu esimerkki 1 Kerätään tiedot taulukkoon: Kilohinta (€/kg) kilomäärä (kg). 1, 90 1, 5 1, 20 x Verrannollisuus

Kun rahamäärä on vakio, kilohinta ja kilomäärä ovat keskenään kääntäen verrannollisia suureita. Jos kilohintaa nostetaan, kilomäärä pienenee. Ratkaistaan kysytty kilomäärä verrannon avulla. (kg) vastaus: Omenoita olisi saanut supermarketista 2, 4 kg. Verrannollisuus

Suoraan ja kääntäen verrannollisuus Suureiden x ja y arvot riippuvat toisistaan taulukon mukaisesti. x: n arvo y: n arvo x 1 y 1 x 2 y 2 Jos x: n ja y: n arvot riippuvat toisistaan suoraan verrannollisesti, on voimassa yhtälö. . Jos taas x: n ja y: n arvot riippuvat toisistaan kääntäen verrannollisesti, yhtälö on Yhtälöä, jossa kahden osamäärän välille on merkitty yhtäsuuruus, nimitetään verrannoksi. Verrannollisuus