Ekonometrija 7 Ekonometrija Osnovne studije Predava Aleksandra Nojkovi

Ekonometrija 7 Ekonometrija, Osnovne studije Predavač: Aleksandra Nojković

Struktura predavanja Klasični višestruki linearni regresioni model posebne teme: • Veštačke promenljive (JB test) Narušavanje pretpostavki KLRM ¡ Slučajna greška nema normalnu raspodelu • Testiranje stabilnosti parametara

Veštačke promenljive ¡ ¡ Koriste se da opišu uticaj kvantitativno nemerljivih faktora na kretanje izabrane zavisne promenljive l U podacima preseka: potrošnja može zavisiti od starosnih, polnih, regionalnih, verskih i drugih razlika. l U podacima vremenskih serija: sezonski efekti, efekti intervencija i strukturnog loma. Definišu se tako da uzimaju vrednost 1 za jedan modalitet i 0 za drugi modalitet.

Veštačke promenljive (primeri primene) ¡ Najčešće obuhvataju uticaje neekonomske prirode: kvalitataivne faktore (pol, bračno stanje, zanimanje, članstvo u sindikatu, pripadnost određenoj rasi, religijske i kulturne razlike) ili privremene efekte (promene u institucionalnom i političkom okruženju, ratni periodi, sezonski efekti). ¡ Međutim, mogu obuhvatati i šire grupe kvantitativnih efekata (dohodak ili godine starosti, kada je dovoljno odabrati nekoliko karakterističnih, širih grupa: npr. potrošači do i preko 35 godina ili oni sa dohotkom do 40000 din, između 40000 -60000 din. i preko 60000 din. ).

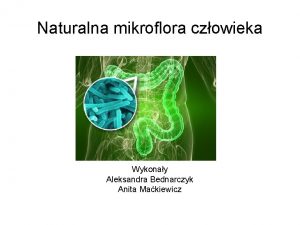
Promena nivoa osnovne inflacije u Srbiji nakon uvođenja PDV

Načini uvođenje u model Ispitujemo zavisnost potrošnje datog proizvoda (Y) od dohotka (X 1) prema uzorku koji se sastoji od gradskih i seoskih domaćinstava): ¡ Yi = β 0 + β 1 X 1 i + εi, i =1, 2, . . . , n Razlika se može ispoljiti u promeni: 1. 2. 3. vrednosti odsečka – slobodnog člana (β 0) vrednost nagiba – marginalne sklonosti ka potrošnji (β 1) i vrednost odsečka i nagiba (β 0 i β 1).

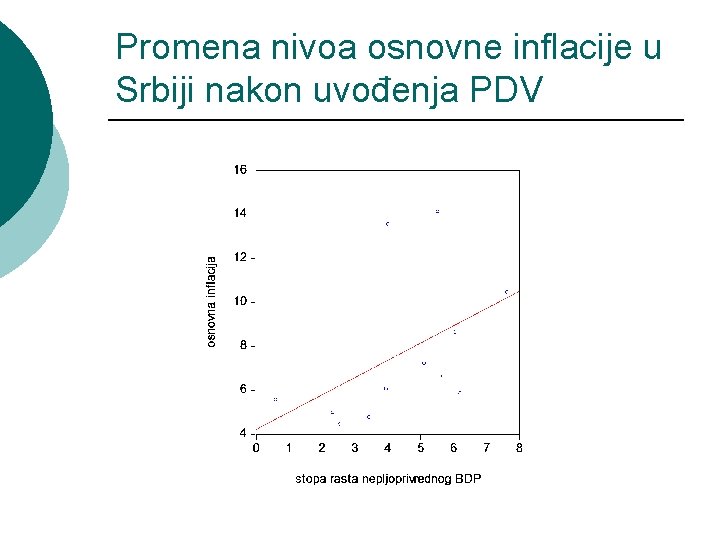
Promena vrednosti odsečka (β 0) ¡ Model koji obuhvata regionalne razlike u nivou potrošnje uključuje veštačku promenljivu V, definisanu kao: ¡ Polazni model postaje: Yi = β 0 + β 1 X 1 i + β 2 V + εi, i =1, 2, . . . , n Odnosno model postaje: - za V = 0 (seoska dom. ): Yi=β 0+β 1 X 1 i+ εi. - za V = 1 (gradska dom. ): Yi = (β 0 +β 2)+ β 1 X 1 i+ εi. ¡

Grafički prikaz promene vrednosti odsečka (β 0)

Promena vrednosti nagiba (β 1) ¡ Ako pretpostavimo da postoji značajna razlika u marginalnoj slonosti ka potrošnji gradskih i seoskih domaćinstava, veštačka promenljiva se uvodi kao: Yi = β 0 + β 1 X 1 i + β 3 VX 1 i + ε i, i =1, 2, . . . , n ¡ Ovom relacijom obuhvaćena su dva modela: - za V = 0 (seoska dom. ): Yi=β 0+β 1 X 1 i+ εi. - za V = 1 (gradska dom. ): Yi=β 0+(β 1+β 3)X 1 i+ εi.

Grafički prikaz promene vrednosti nagiba (β 1)

Promena vrednosti odsečka i nagiba (β 0 i β 1) ¡ Polaznu funkciju proširujemo sa dve promenljive V i VXi i model postaje: Yi = β 0 + β 1 X 1 i + β 4 V + β 5 VX 1 i + εi. ¡ Jednačinu je moguće raščlaniti na dve funkcije: Yi = β 0 + β 1 X 1 i + εi, za seoska domać. Yi = (β 0+β 4) + (β 1+β 5)X 1 i+ εi, za gradska domać.

Grafički prikaz promene vrednosti odsečka (β 0) i nagiba (β 1)

Interakcija različitih faktora ¡ ¡ Za istarživanje interakcije različitih faktora formiraju se nove veštačke promenljive kao proizvodi već definisanih veštačkih promenljivih. Ako pretpostavimo da se ocenjuje uticaj pola i dve kategorije domaćinstava (gradska i seoska) na potrošnju nekog proizvoda, onda model postaje: Yi = β 0 + β 1 X 1 i + β 2 V 1 + β 3 V 2 + β 4 V 3 + ε i, gde su veštačke promenljive definisane kao: i dok je interakcija V 3=V 1 V 2=

Pravila ocenjivanja modela sa veštačkim promenljivima ¡ ¡ ¡ Dodeljivanje vrednosti 0 i 1 za pojedine modalitete potpuno je proizvoljno i ne menja konačne zaključke. Broj veštačkih promenljivih uvedenih u model uvek je za jedan MANJI od broja modeliteta (izbegavamo “ zamku veštačke promenljive “). Identični rezultati dobijaju se ocenjivanjem dve odvojene regresije, kada raspolažemo dovoljnim brojem podataka.

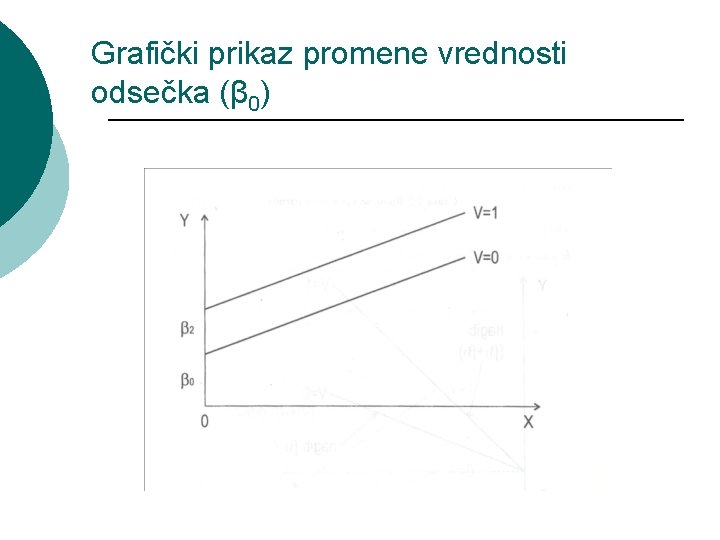
Testiranje sezonskih efekata ¡ ¡ Izražena sezonska priroda pojedinih ekonomskih promenljivih modelira se uvođenjem sezonskih veštačkih promenljivih. Na primer, potrošnja sladoleda pre capita (Y) zavisi od realnog dohotka (X 1), relativne cene (X 2) i godišnjeg doba, što predstavljamo modelom: Yi = β 0 + β 1 X 1 + β 2 X 2 + β 3 S 1 + β 4 S 2 + β 5 S 3 + εi, gde smo sa S 1, S 2 i S 3 označili sezonske veštačke promenljive definisane kao: ¡ Dovoljne su TRI veštačke promenljive za obuhvatanje ČETIRI modaliteta !

Sezonski karakter vremenskih serija srpske privrede Mesečni podaci Kvartalni podaci

Testiranje asimetričnih efekata ¡ ¡ Asimetričan efekat: jedinični porast i jedinični pad objašnjavajuće promenljive izazivaju različitu (po apsolutnoj vrednosti) promenu zavine promenljive. Ukoliko posmatramo potrošnu funkciju: pri čemu je prosečna potrošnja izražena parametrom β 1. ¡ Ukoliko je efekat rasta i pada dohotka asimetričan, uvodimo veštačku promenljivu A kao: tako da ocenjujemo model oblika:

Sta kada je zavisna promenljiva veštačka? Mikroekonometrijski modeli kvalitativene (diskretne) zavisne promenljive: LMV, probit i logit (nisu predmet razmatranja ovog kursa).

KLRM pretpostavka 5: Slučajna greška ima normalnu raspodelu ¡ Ukoliko je samo ova pretpostavka narušena primenom metoda ONK se dobijaju najbolje linearne nepristrasne ocene. ¡ Postupak statističkog zaključivanja je pogrešan ¡ Testiranje hipoteza je nepouzdano.

Kako se proverava pretpostavka da slučajna greška ima normalnu raspodelu? ¡ Neformalni histograma (grafički) metodi – Analiza ¡ Formalno testiranja - Žark-Bera (engl. Jarque. Bera) test normalnosti

Koeficijenti kojima se opisuju svojstva raspodela ¡ Empirijska raspodela se opisuje sa dva koeficijenta: asimetrije i spljoštenosti. ¡ Koeficijent asimetrije meri stepen u kojem raspodela nije simetricna oko srednje vrednosti (simetricna raspodela, asimetricna u levo ili u desno), α 3: N(0, 6/n). ¡ Koeficijent spljoštenosti meri debljinu repa raspodele, α 4: N(3, 24/n). - Kada postoje ekstremni dogadaji tada su repovi teži od repova normalne raspodele ¡ Veca spljoštenost – repovi su lakši ¡ Manja spljoštenost – repovi su teži.

JB test statistika ¡ Način izračunavanja: ¡ Postupak testiranja: H 0: serija ima normalnu raspodelu H 1: serija nije normalno raspodeljena ¡ Kritična vrednost na nivou značajnosti 5% je 5. 99 (važi asimptotski!)

Šta raditi u slučaju da raspodela odstupa od normalne? ¡ Ne postoji jedinstveno rešenje. ¡ Mogu se koristiti metode testiranja koje ne pretpostavljaju normalnost, ali su one izuzetno komplikovane i njihova svojstva nisu poznata. ¡ Najčešće se modifikuje polazna specifikacija uključivanjem promenljivih kojima će se eksplicitno modelirati ekstremni događaji. Takve promenljive se nazivaju veštačke promenljive.

Testiranje stabilnosti ocena ¡ Implicitna pretpostavka regresione analize odnosi se na stabilnost parametara (nepromenjivost za sve opservacije u uzorku). ¡ Analiza stabilnosti parametara potrebna je kao provera pouzdanosti modela u predviđanju. ¡ Za ispitivanje stabilnosti ocena koristi se Fstatistika testa (složena hipoteza) - dve verzije Chow testa.

Tetsiranje stabilnosti parametara Posmatramo model oblika: Yt=β 0+β 1 X 1 t+εt, čiji se parametri ocenjuju na osnovu n opservacija vremenskih serija (t=1, 2, . . . , n). Pretpostavimo da se prvih n 1 opservacija odnose na jedan režim poslovanja, a narednih n 2 opservacija na period promenjenog ekonomskog okruženja (ukupno n=n 1+n 2). ¡ ¡ Polazni model proširujemo na sledeći način: Yt = β 0 + β 1 X 1 t + β 2 V + β 3 VX 1 t + εt.

Testiranje stabilnosti parametara (test dodatih regresora) ¡ Definišemo nultu i altenativnu hipotezu: H 0: β 2=β 3=0 (parametri su stabilni) H 1: β 2 i/ili β 3 su statistički značajni (parametri su nestabilni). ¡ Polazni model možemo smatrati modelom sa ograničenjem, gde je broj ograničenja (g=2), jednak broju dodatih parametara.

Chow test (prva verzija) Pretpostavimo da je prvobitni uzorak n 1, a za period predviđanja imamo još dodanih n 2 opservacija (ukupno n=n 1+n 2), engl. Chow Forecast Test. ¡ Nulta hipoteza da su reg. parametri ostali nepromenjeni i u proširenom modelu: H 0: B 1=B, testira se ispitujući značajnost rezidualne sume kvadrata iz proširenog (e’e) i prvobitnog uzorka (e 1’e 1). ¡ ¡ Potrebno je oceniti dve odvojene regresije (sa n 1 i n opservacija).

Chow test (druga verzija) ¡ Testira se prisustvo strukturnog loma (preloma) u tački t *, koja deli uzorak veličine n na dva poduzorka, veličine n 1 i n 2 (engl. Chow Breakpoint Test). ¡ Porede se sume kvadrata reziduala dobijene ocenjivanjem dve odvojene regresije na bazi skupa opservacija n 1 i n 2, sa onom dobijenom iz polazne regresije na osnovu svih n opservacija: pri čemu količnik meri prirast do kojeg dolazi usled ocenjivanja celog uzorka (ako je ovaj prirast značajan, zbir dve odvojene sume reziduala je manji od ukupne).

Chow test (druga verzija)- nastavak ¡ Potrebno je oceniti tri odvojene regresije (na bazi n 1, n 2 i n opservacija) ¡ Hipoteza se definiše kao: H 0: Parametri su stabilni (opravdano je oceniti jednu regresiju na bazi svih n opservacija) H 1: Parametri su nestabilni (opravdano je oceniti dve odvojene regresije). ¡ Zaključak: Značajan prirast sume kvadrata reziduala u regresiji sa svih n opservacija - opravdano je oceniti dve odvojene regresije, tj. parametri su nestabilni.

Rekurzivna regresija ¡ Postupak se sastoji iz sledećih koraka: - Regresiona jednačina sa k parametara za ocenjivanje se ocenjuje počevši od prvih k opservacija. - Svaki put se dodaje po još jedna opservacija i postupak ponavlja dok nisu iskorišćene sve opservacije (n-k koraka). - U svakom koraku se ocenjuje sledeća očekivana vrednost zavisne promenljive i računa rekurzivni rezidual (razlika stvarne i ocenjene vrednosti zavisne promenljive).

Rekurzivna regresija ¡ 1) 2) 3) Analiza stabilnosti koja se zasniva na primeni NK: Rekurzivni reziduali – ucrtavaju se oko nulte linije za svaku iteraciju , plus i minus dve st. greške. Reziduali izvan ovih granica sugerišu nestabilnost modela. CUSUM test (obe verzije) – zasniva se na kumulativnoj sumi svih prethodnih rekurzivnih reziduala, deljenih njihovom dotadašnjom standardnom greškom. Ako vektor parametara ne ostaje konstantan u celom uzorku (istupa izvan granica), parametri su nestabilni. Rekurzivni koeficijenti -polazi se od regresije sa min. brojem k-opservacija, pa se sve više opservacija uključuje u uzorak. Pojedinačni koeficijenti su dati uz pojas od plus i minus dve st. greške. Značajne varijacije ocenjenih koeficijenata pri dodavanju novih varijacija ukazuju na nestabilnost.