Ekonometria WYKAD 7 Piotr Cikowicz Katedra Midzynarodowych Studiw

Ekonometria WYKŁAD 7 Piotr Ciżkowicz Katedra Międzynarodowych Studiów Porównawczych

Plan Czym się zajmiemy: 1. Procesy stochastyczne 2. Stacjonarność procesu 3. Testowanie stacjonarności 4. Modele z rozkładem opóźnień

Podstawowe definicje ► Proces stochastyczny: zbiór zmiennych losowych {Y(t)} uporządkowany według indeksu czasu t ► Szereg czasowy {y(t)} to realizacja procesu stochastycznego {Y(t)} w próbie ► Przykład 1: ► proces stochastyczny może opisywać statystyczny rozkład prędkości kulki toczącej się po pochylni w czasie ► szereg czasowy będący realizacją takiego procesu składa się z pomiaru prędkości kulki dla jednej próby puszczenia jej po pochylni ► Przykład 2: ► szereg czasowy dynamiki PKB w Polsce w latach 19962010. ► proces stochastyczny - ?

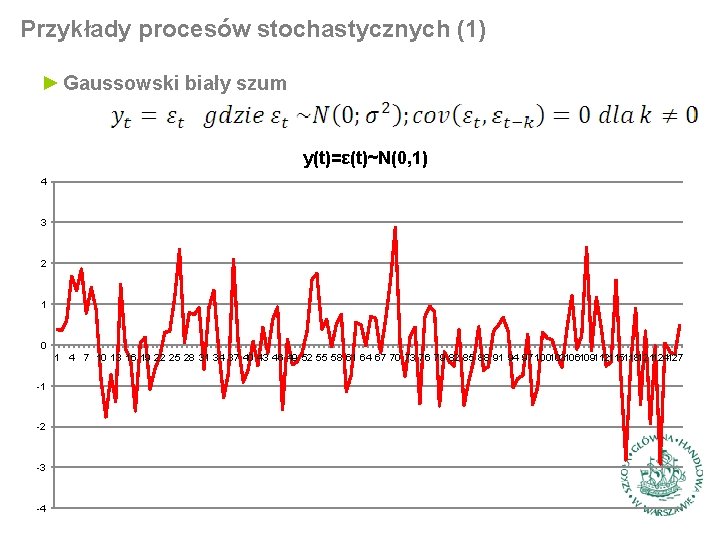
Przykłady procesów stochastycznych (1) ► Gaussowski biały szum y(t)=ε(t)~N(0, 1) 4 3 2 1 0 1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 73 76 79 82 85 88 91 94 97 100103106109112115118121124127 -1 -2 -3 -4

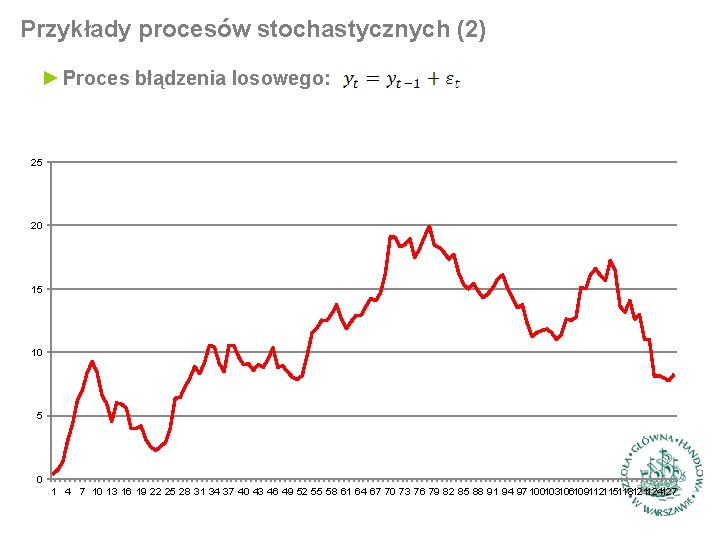
Przykłady procesów stochastycznych (2) ► Proces błądzenia losowego: 25 20 15 10 5 0 1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 73 76 79 82 85 88 91 94 97 100103106109112115118121124127

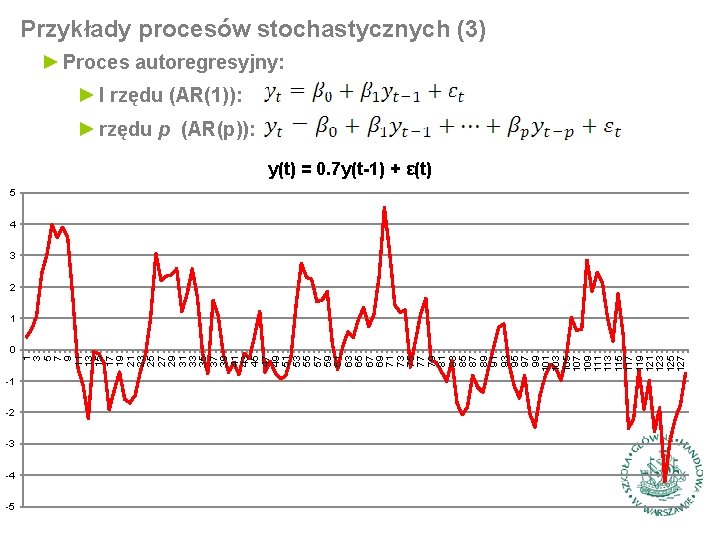
Przykłady procesów stochastycznych (3) ► Proces autoregresyjny: ► I rzędu (AR(1)): ► rzędu p (AR(p)): y(t) = 0. 7 y(t-1) + ε(t) 5 4 3 2 0 -1 -2 -3 -4 -5 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 127 1

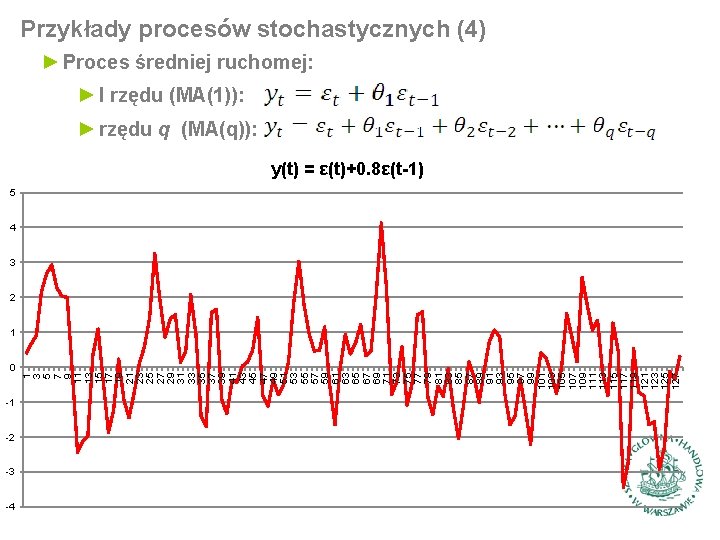
0 -1 -2 -3 -4 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 127 Przykłady procesów stochastycznych (4) ► Proces średniej ruchomej: ► I rzędu (MA(1)): ► rzędu q (MA(q)): y(t) = ε(t)+0. 8ε(t-1) 5 4 3 2 1

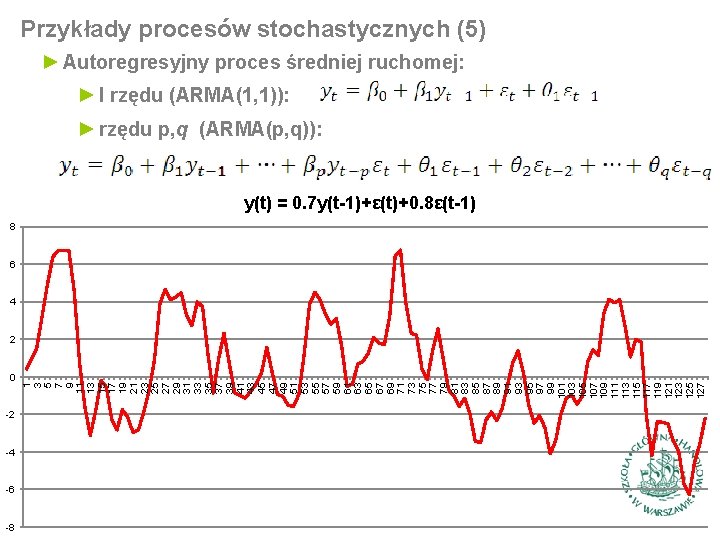
Przykłady procesów stochastycznych (5) ► Autoregresyjny proces średniej ruchomej: ► I rzędu (ARMA(1, 1)): ► rzędu p, q (ARMA(p, q)): y(t) = 0. 7 y(t-1)+ε(t)+0. 8ε(t-1) 8 6 4 0 -2 -4 -6 -8 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 127 2

Stacjonarność procesu stochastycznego (1) ► Proces stochastyczny jest ściśle stacjonarny jeśli jego wszystkie charakterystyki nie zmieniają się w czasie ► Proces stochastyczny jest słabo stacjonarny jeśli wartość oczekiwana, wariancja i kowariancja są stałe w czasie tzn. ► W ekonomii większość analizowanych szeregów ma charakter niestacjonarny (np. poziom PKB, poziom cen, wielkość długu publicznego itp. ) ► Modelowanie ekonometryczne na podstawie szeregów niestacjonarnych prowadzi do zjawiska regresji pozornej (omówione dalej)

Stacjonarność procesu stochastycznego (2) ► Przykład: stacjonarność procesu błądzenia losowego ► Proces błądzenia losowego można zapisać jako: … ► Dla y(0)=0, wartość oczekiwana i wariancja procesu to:

Stacjonarność procesu stochastycznego (3) ► Proces błądzenia losowego jest szczególnym przypadkiem procesu AR(1) postaci , który jest stacjonarny gdy zachodzi ► Jeśli warunek ten jest spełniony to proces jest stacjonarny, gdyż wpływ zaburzenia losowego wygasa w czasie tzn. ► Proces AR(1) można przedstawić jako: … ► To oznacza, że

Stacjonarność procesu stochastycznego (4) ► Proces błądzenia losowego jest procesem niestacjonarnym, lecz jego przyrosty są stacjonarne. ► Jeśli z każdej strony równania błądzenia losowego odejmiemy y(t-1), to otrzymamy: co można zapisać jako: ► Jeśli proces jest niestacjonarny, ale jego pierwsze przyrosty, czyli różnice między kolejnymi obserwacjami szeregu są stacjonarne, to jest to szereg zintegrowany w stopniu 1 i zapisujemy

Stacjonarność procesu stochastycznego (5) ► Ogólniej: jeśli d-krotne różnicowanie sprowadza proces do stacjonarności, to proces jest zintegrowany stopnia d co zapisujemy jako ► Przykład: szereg postaci zintegrowany stopnia 2 , bo jest ► Proces, który różnicowaniem można doprowadzić do stacjonarności nazywamy przyrostostacjonarnym i mówimy, że wykazuje trend stochastyczny ► Trend może mieć też charakter trendu deterministycnzego, jeśli szereg jest trendostacjonarny np.

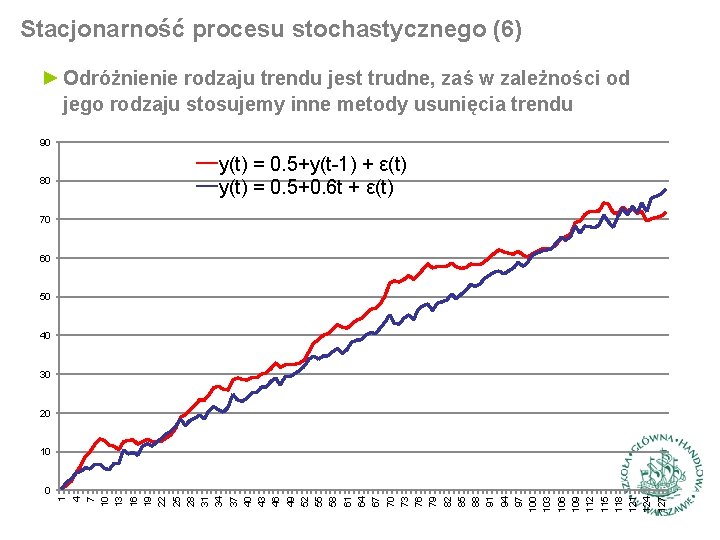
Stacjonarność procesu stochastycznego (6) ► Odróżnienie rodzaju trendu jest trudne, zaś w zależności od jego rodzaju stosujemy inne metody usunięcia trendu 90 80 y(t) = 0. 5+y(t-1) + ε(t) y(t) = 0. 5+0. 6 t + ε(t) 70 60 50 40 30 20 0 1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 73 76 79 82 85 88 91 94 97 100 103 106 109 112 115 118 121 124 127 10

Testowanie stacjonarności (1) ► Testowanie na podstawie funkcji autokorelacji (ACF – autocorrelation function) procesu postaci: ► Dla szeregu czasowego będącego realizacją procesu funkcja przyjmuje postać: ► Dla białego szumu wartości ACF są równe 0 dla każdego k, zaś dla procesu błądzenia losowego są równe 1 ► Dla procesu AR(1) można pokazać, że ► Jeśli wartości ACF zaczynają się od ok. 1 i zbiegają powoli do zera, to można podejrzewać niestacjonarność procesu

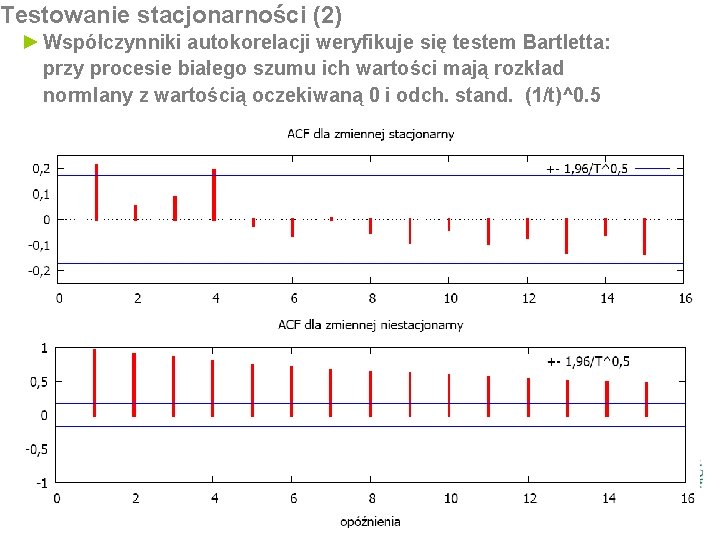
Testowanie stacjonarności (2) ► Współczynniki autokorelacji weryfikuje się testem Bartletta: przy procesie białego szumu ich wartości mają rozkład normlany z wartością oczekiwaną 0 i odch. stand. (1/t)^0. 5

Testowanie stacjonarności (3) ► Funkcja ACF – pierwsze przybliżenie, ale nie formalny test stacjonarności ► Najczęściej stosowany test stacjonarności to test Dickeya -Fullera ► Podstawa testowania te proces AR(1) ► Jeśli to proces jest stacjonarny ► Przetestowanie hipotezy testem t-Studenta nie jest możliwe, bo dla procesu niestacjonarnego statystyka t-Studenta nie ma rozkładu t-Studenta ► Testowaniu podlega przekształcona postać procesu tzn. ► Hipotezy to

Testowanie stacjonarności (4) ► Hipotezę zerową weryfikuje się statystyką DF postaci porównując ją ze statystyką odczytaną z tablic ► Uwaga! Statystyka DF, pomimo postaci statystyki t-Studenta nie ma rozkładu t-Studenta, jeśli nie odrzucamy hipotezy zerowej ► Procedura testowa testu DF: ► Oszacowanie modelu ► Wyznaczenie DF i sprawdzenie z wartością z tablic. Jeśli wyznaczona statystyka DF jest mniejsza od statysstyki z tablic (tzn. bardziej ujemna) to odrzucamy H 0 i proces jest stacjonarny ► Jeśli jest większa (tzn. mniej ujemna) to nie odrzucamy H 0. Oznacza to, że proces może być I(1), ale również I(2) lub I(3). ► Powtarzamy procedurę dla ► Jeśli odrzucimy H 0, to proces jest I(1), jeśli nie, to proces jest I(2) lu zintegrowany wyższych rzędów ► W praktyce nie występują procesu wyższych rzędów niż I(2) więc wskazuje to raczej na słabość testu.

Testowanie stacjonarności (5) ► Inne postacie testu DF: ► Test ADF (Augmented Dickey Fuller) – pozwala uwzględnić potencjalną autokorelację składnika losowego. Równanie testowe ma postać (k to najmniejsza opóźnienie, przy którym składnik losowy nie wykazuje autokorelacji) ► Test DF uwzględniający stałą i/lub trend deterministyczny postaci lub ► W praktyce dobór postaci testu nie jest łatwy. Zazwyczaj test DF uzupełnia się też stosowanie innych testów, z hipotezą zerową mówiącą o stacjonarności szeregu (np. test KPSS).

Modele z rozkładem opóźnień (1) ► Zależność między zmiennymi makroekonomicznymi często rozciąga się w czasie na więcej niż 1 okres ► W najprostszym przypadku zmienna objaśniana może być funkcją wartości bieżących i skończonej liczby opóźnień zmiennej objaśniającej. Taki model nazywa się modelem ze skońconym rozkładem opóźnień rzędu P (zapisujemy jako DL(P) ► Współczynnik określa bezpośredni (natychmiastowy) wpływ zmian bieżących wartości x na bieżące wartości y, stąd nazywany jest mnożnikiem bezpośrednim lub krótkookresowym ► Zmiana x w okresie t wpływa również na wartość y w okresie t+1, t+2 … t+p z siłą równą odpowiednim wspołczynnikom. Łączny wpływ jednostkowej zmiany x na y to mnożnik długookresowy i wynosi

Modele z rozkładem opóźnień (2) ► W bardziej złożonym przypadku zmienna objaśniająca jest dodatkowo funkcją własnych opóźnionych wartości. ► Taki model to model autoregresyjny z rozkładem opóźnień (Autregressive Distribted Lag – ADL) – ADL(Q, P) - postaci ► Mnożnik długookresowy wyznacza się zakładając, że obie zmienne przyjmują swoją długookresową wartość. Dla zmiennych stacjonarnych są one równe wartościom oczekiwanym stąd zakładając mamy:

Dziękuję za uwagę