Vitalii Dugaev Katedra Fizyki Politechnika Rzeszowska Semestr zimowy

Vitalii Dugaev Katedra Fizyki Politechnika Rzeszowska Semestr zimowy, rok 2012/2013

[1] D. Halliday, R. Resnick, J. Walker. Podstawy fizyki. [2] M. Massalska, J. Massalski. Fizyka dla inżynierów. [3] A. A. Dietłaf, B. M. Jaworski. Fizyka. Poradnik encyklopedyczny [4] Berkley Physics Course. [5] H. D. Young, R. A. Freedman. University Physics. [6] R. A. Serwey, J. W. Jewett. Physics for Scientists and Engineers. Lekcja 1 Strona 2

Lekcja 1 Strona 3

Lekcja 1 Strona 4

Lekcja 1 Strona 5

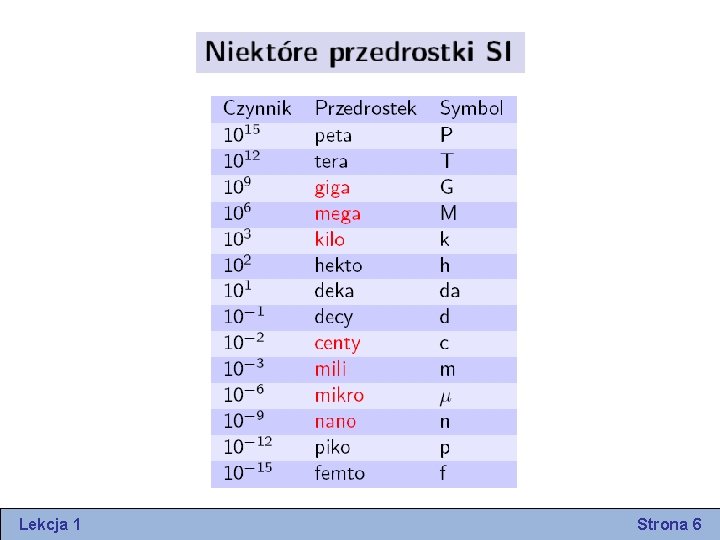
Lekcja 1 Strona 6

Błędy i niepewności pomiarów Lekcja 1 Strona 7

Błąd pomiaru - różnica między wynikiem pomiaru a wartością mierzonej wielkości fizycznej. Bywa też nazywany błędem bezwzględnym pomiaru. Ponieważ wartość wielkości mierzonej (wartość prawdziwa) jest w praktyce niepoznawalna, to w celu określenia błędu posługujemy się poniższymi, bardziej precyzyjnymi terminami. Ścisłe określenie, co to jest wartość prawdziwa, zależy od użytej teorii fizycznej (fizyka klasyczna lub kwantowa). Błąd przypadkowy - różnica między wynikiem pomiaru a średnią arytmetyczną nieskończonej liczby wyników pomiarów tej samej wielkości mierzonej, wykonanych w warunkach powtarzalności. Błąd przypadkowy jest wynikiem nieprzewidywalnych zmian przypadkowych czynników wpływających na pomiar; daje on przyczynek wpływający na rozrzut wyników. Lekcja 1 Strona 8

Błąd systematyczny - różnica między średnią arytmetyczną nieskończonej liczby wyników pomiarów tej samej wielkości mierzonej, wykonanych w warunkach powtarzalności, a wartością wielkości mierzonej. Błąd systematyczny jest również wynikiem czynników wpływających na pomiar, ale czynniki te można rozpoznać. Obowiązkiem eksperymentatora jest wprowadzenie poprawki kompensującej błąd systematyczny. Błąd względny - stosunek błędu pomiaru do wartości wielkości mierzonej. Lekcja 1 Strona 9

Niepewność pomiaru - parametr związany z wynikiem pomiaru, charakteryzujący rozrzut wartości wielkości mierzonej, który można w uzasadniony sposób przypisać wielkości mierzonej. Na pełną niepewność pomiaru powinny składać się wszystkie przyczynki pochodzące od rozrzutu wyników, rozkładu prawdopodobieństwa przyjętego na podstawie wiedzy o mierzonej wielkości, o jej pomiarach, wykorzystanych przyrządach pomiarowych lub przyczynki wynikające z doświadczenia eksperymentatora. Niepewność pomiaru wielkości x oznaczamy literą u(x) (od angielskiego słowa ”uncertainty”) Lekcja 1 Strona 10

Pomiary bezpośrednie Obliczanie niepewności standardowej metodą typu A • dysponujemy zestawem pomiarów powtarzanych w jednakowych warunkach, a obliczenie niepewności dokonuje się drogą analizy statystycznej Odchylenie standardowe σ dla pojedynczego pomiaru jest miarą średniego rozrzutu wyników pomiarów wokół prawdziwej wartości mierzonej wielkości (wartości oczekiwanej) Lekcja 1 Strona 11

Odchylenie standardowe średniej jest mniejsze niż odchylenie standardowe pojedynczego pomiaru i wyraża się wzorem Stanowi ono niepewność standardową obliczoną metodą typu A. Powyższy wzór jest wyrazem faktu, że średnia chociaż, tak jak wynik pojedynczego pomiaru, nie jest równa wartości prawdziwej, to jednak leży ona bliżej wartości prawdziwej, niż pojedynczy pomiar. Lekcja 1 Strona 12

Obliczanie niepewności standardowej metodą typu B • dostępny jest tylko jeden wynik pomiaru, lub gdy wyniki nie wykazują rozrzutu. Wówczas niepewności standardowej nie można obliczyć drogą analizy statystycznej i ocenia się ją na podstawie danych umieszczonych w specyfikacji przyrządu pomiarowego, wiedzy o danej wielkości fizycznej lub o przedziale, w którym wartość rzeczywista powinna się mieścić. W laboratorium studenckim najprostsza metoda obliczania niepewności typu B polega na uwzględnieniu niepewności maksymalnej x, będącej połową szerokości przedziału, w jakim zmierzone wartości powinny się mieścić Lekcja 1 Strona 13

Jeżeli obydwa typy niepewności występują równocześnie, należy posłużyć się prawem składania niepewności, które prowadzi do następującej zależności na niepewność standardową łączną: Lekcja 1 Strona 14

Obliczanie niepewności wielkości złożonej Lekcja 1 Strona 15

Przykład Wyznaczamy wartość przyspieszenia ziemskiego mierząc czas równy 10 okresom drgań wahadła matematycznego o długości 1. 35 m. Wartości tych czasów są następujące 23. 3 23. 5 23. 6 23. 2 23. 4 23. 5 23. 4 23. 3 23. 4 23. 7 23. 1 23. 6 23. 5 23. 7 23. 2 23. 3 23. 2 23. 7 23. 3 23. 4 Wartość średnia tśr = 23. 42 s, odchylenie standardowe u(t)=0. 039 s. Okres drgań T = 2. 34 s, u(T) = 0. 004 s. Długość wahadła zmierzono z dokładnością l = 0. 5 cm, u(l) = 0. 003 m. Lekcja 1 Strona 16

Lekcja 1 Strona 17

Wartość tablicowa przyspieszenia ziemskiego g = 9. 81 m/s 2. Różnica pomiędzy wartością zmierzoną a tablicową 9. 81 - 9. 73 = 0. 08 m/s 2 Lekcja 1 Strona 18

Zaokrąglanie wyników pomiaru Jeżeli uzyskana w wyniku obliczeń masa wynosi m = 0. 02145 kg, a niepewność u(m) = 3. 751 g = 0. 003751 kg, to najpierw zaokrąglona do dwóch cyfr znaczących niepewność wynosi u(m) = 0. 0038 kg, a zaokrąglony następnie wynik pomiaru (tutaj do czterech cyfr po przecinku) to m = 0. 0214 kg. Razem wynik zapiszemy jako: m = (0. 0214 ± 0. 0038) kg lub jeszcze lepiej: m = (21. 4 ± 3. 8)∙ 10 -3 kg Poniższe zaokrąglenia, jakkolwiek formalnie poprawne, są z fizycznie niepoprawne: Lekcja 1 m = (0. 0214 ± 0. 00375) kg źle m = (0. 02145 ± 0. 0038) kg źle m = (0. 021 ± 0. 0038) kg źle Strona 19

Średnia ważona wagą jest odwrotność niepewności standardowej średnia arytmetyczna Lekcja 1 Strona 20

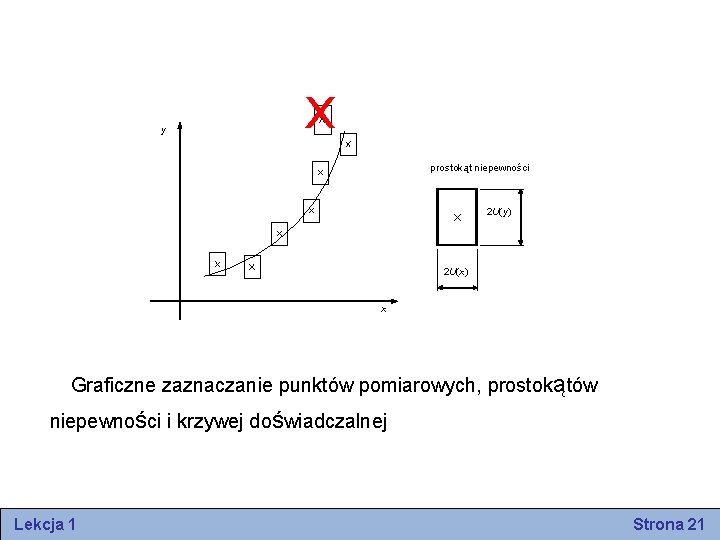
y x x prostokąt niepewności 2 U(y) 2 U(x) x Graficzne zaznaczanie punktów pomiarowych, prostokątów niepewności i krzywej doświadczalnej Lekcja 1 Strona 21

Metoda najmniejszych kwadratów Lekcja 1 Strona 22

Lekcja 1 Strona 23

estymator jednakowych odchyłek standardowych zmierzonych wartości yi Lekcja 1 Strona 24

p(x) Lekcja 1 Strona 25

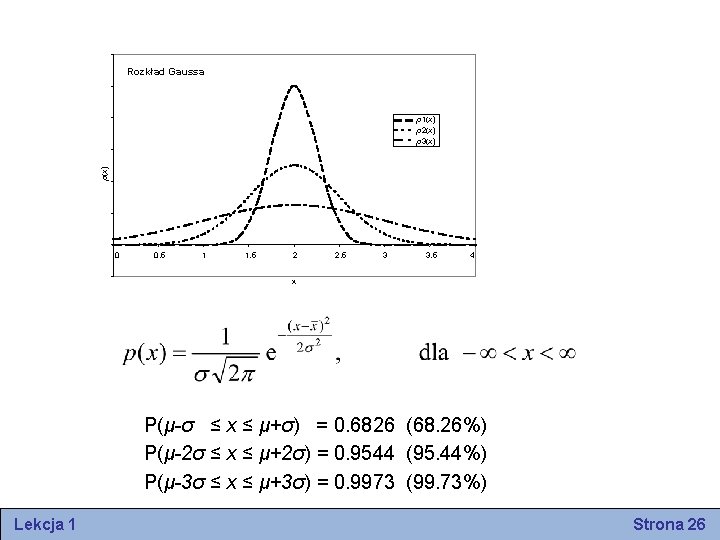
Rozkład Gaussa p(x) p 1(x) p 2(x) p 3(x) 0 0, 5 1 1, 5 2 2, 5 3 3, 5 4 X P(μ-σ ≤ x ≤ μ+σ) = 0. 6826 (68. 26%) P(μ-2σ ≤ x ≤ μ+2σ) = 0. 9544 (95. 44%) P(μ-3σ ≤ x ≤ μ+3σ) = 0. 9973 (99. 73%) Lekcja 1 Strona 26

Lekcja 1 Strona 27

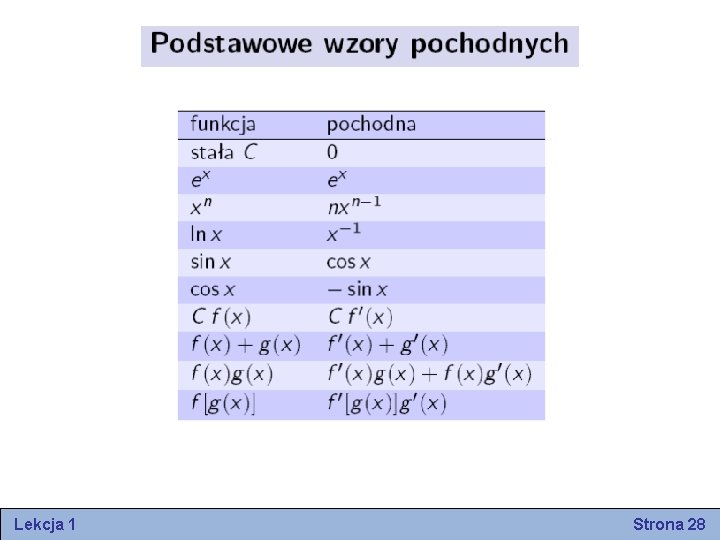
Lekcja 1 Strona 28

Lekcja 1 Strona 29