EKONOMETRIA PREDNKA 2 LINERNY EKONOMETRICK MODEL S DVOMI

EKONOMETRIA PREDNÁŠKA 2 LINEÁRNY EKONOMETRICKÝ MODEL S DVOMI PREMENNÝMI 1

Obsah prednášky: LINEÁRNY EKONOMETRICKÝ MODEL S DVOMI PREMENNÝMI 2. 1 Predpoklady lineárneho ekonometrického modelu s dvomi premennými 2. 2 Odhad parametrov lineárneho ekonometrického modelu s dvomi premennými 2. 3 Štatistické vlastnosti odhadovej funkcie najmenších štvorcov Otázky k 2. PREDNÁŠKE 2

Najjednoduchším ekonometrickým modelom je lineárny model, v ktorom je jedna premenná Y závislá iba od jednej nezávisle premennej X a aditívnej náhodnej poruchy: (2. 1) Pri modelovaní ekonomických vzťahov sa len málokedy stretneme s takýmto jednoduchým modelom, budeme sa ním podrobne zaoberať hlavne kvôli jeho jednoduchosti, názornosti a možnosti grafického znázornenia. Z modelu (2. 1) vyplýva, že podmienená stredná hodnota endogénnej premennej Y je lineárnou funkciou exogénnej premennej X: (2. 2) Zo vzťahu (2. 2) je zrejmé, že s rastom premennej X rastie v priemere aj premenná Y. Označenie „ v priemere“ znamená, že niektoré pozorovania endogénnej premennej nemusia nutne rásť s rastom premennej X. Odchýlky endogénnej premennej od podmienenej strednej hodnoty t. j. od hodnoty endogénnej premennej ležiacej na skutočnej regresnej priamke, možno vyjadriť: (2. 3) 3

(2. 4) kde ui je náhodná premenná, ktorá sa nazýva náhodnou poruchou, náhodnou chybou. Zo vzťahov (2. 2) a (2. 4) vyplýva: (2. 5) Zo vzťahu (2. 5) vyplýva, že i - tá hodnota endogénnej premennej Y sa rovná priemernej hodnote Y všetkých pozorovaní s hodnotou exogénnej premennej Xi plus náhodná odchýlka ui , ktorá môže mať kladnú aj zápornú hodnotu: (2. 6) Zo vzťahu vyplýva že rovnica platí ako rovnosť len vtedy ak : (2. 7) to znamená, že podmienená stredná hodnota náhodnej poruchy sa rovná nule, a vyplýva z predpokladu, že regresná priamka prechádza cez podmienené stredné hodnoty endogénnej premennej. O náhodnej poruche sme zatiaľ predpokladali, že vyjadruje súhrnný vplyv tých premenných, ktoré neboli do modelu z rôznych dôvodov zaradené. Mnoho z nezaradených premenných (hoci merateľných) pôsobia navzájom protichodne, takže ich výsledný efekt na endogénnu premennú, zahrnutú do náhodnej zložky je malý až 4 zanedbateľný a nesystematický.

V chovaní endogénnej premennej (aj pri zaradení všetkých vysvetľujúcich premenných), existuje určitá náhodnosť, ktorá sa nedá vysvetliť. Ekonometrické modeli sú v konečnom dôsledku modelmi správania ľudí v rôznych ekonomických úlohách, ako spotrebiteľov, výrobcov, investorov. . Ich správanie je úplne racionálne a bez zvyšku vysvetliteľné a predvídateľné. Náhodná porucha obsahuje teda vplyv všetkých nezaradených vysvetľujúcich premenných, ale aj túto „čistú“ náhodnosť v správaní ekonomických subjektov. 5

2. 1 Predpoklady lineárneho ekonometrického modelu s dvomi premennými Ak predpokladáme, že ekonomická hypotéza je formulovaná ekonometrickým modelom v tvare lineárneho regresného modelu, a máme k dispozícii n pozorovaní hodnôt premenných Y a X, môžeme model (2. 1) prepísať do tvaru: i = 1, 2, . . . , n (2. 8) Komplexná špecifikácia lineárneho regresného modelu predpokladá okrem špecifikácie lineárneho vzťahu, aj špecifikáciu rozdelenia pravdepodobnosti náhodných porúch ui, ako aj predpoklad o tom, ako sú generované hodnoty exogénnej premennej X. Tieto informácie je možné sformulovať do základných, tzv. klasických predpokladov lineárneho modelu: Predpoklad 1: Náhodné poruchy majú vo všetkých pozorovaniach nulovú strednú hodnotu: i = 1, 2, . . . , n (2. 9) Predpoklad 2: Rozptyl náhodných porúch je vo všetkých pozorovaniach rovnaký (konštantný): i = 1, 2, . . . , n (2. 10) 6

Predpoklad 3: Náhodné poruchy nie sú navzájom korelované, tz. ich kovariancie sú rovné nule i = 1, 2, . . . , n (2. 11) Predpoklad 4: Exogénna (vysvetľujúca) premenná X je nenáhodná, t. j. jej hodnoty Xi sú v opakovaných výberoch fixné, rozptyl jej hodnôt okolo priemeru je nenulový. Predpoklad 5: Náhodné poruchy majú normálne rozdelenie: (2. 12) Splnenia týchto predpokladov zaručuje, že metódy odhadu parametrov lineárneho modelu majú určité dobré vlastnosti, ak nie sú splnené, odhady parametrov strácajú niektoré z týchto dobrých vlastností. Predpoklady 1 až 5 predstavujú požiadavky klasickej štatistiky, ktoré však v ekonometrii nemusia byť vždy splnené, pretože ekonomické dáta nie sú generované kontrolovaným experimentom. Metódy klasickej štatistiky boli vyvinuté pre účely analýzy experimentálnych dát, ktoré predpoklady 1 až 5 spĺňajú. 7

Splnenie predpokladu 1 znamená, že náhodná premenná ui má vo všetkých pozorovaniach nulovú strednú hodnotu. Predpoklad 2 sa označuje ako predpoklad homoskedasticity. Podľa neho majú náhodné poruchy vo všetkých pozorovaniach rovnaký rozptyl , ktorý však nepoznáme. Lineárny model (2. 8) má teda nie dva, ale tri neznáme parametre a . Variabilitu náhodných porúch je možné vypočítať: (2. 13) V prípade porušenia tohto predpokladu (ak neplatí), náhodné poruchy nemajú konštantný rozptyl model je heteroskedastický. Heteroskedasticita je typická najmä pre prierezové dáta, u časových radov sa vyskytuje v menšej miere. Predpoklad 3 sa vzťahuje k vlastnosti náhodných porúch o ich vzájomnej neskorelovanosti, (nulovej kovariancie): (2. 14) Ak platí vzťah (2. 14), znamená to, že pre náhodné poruchy z rôznych pozorovaní sú nezávislé. V opačnom prípade, ak vzťah (2. 14) neplatí, hovoríme o sériovej korelácii náhodných porúch resp. autokorelácii. Autokorelácia (podobne ako heteroskedasticita) teda označuje situáciu, keď v správaní náhodných porúch je prítomný určitý systematický prvok. 8

Predpoklad 4 definuje požiadavku pre vysvetľujúcu premennú, pre ktorú platí, že nie je generovaná náhodným procesom. Znamená to, že vysvetľujúca premenná je nestochastická, alebo ak aj je stochastická, nie je korelovaná s náhodnou poruchou tj. : (2. 15) Posledný predpoklad 5 o normálnom rozdelení náhodných porúch, vyplýva z chyby špecifikácie vysvetľujúcich premenných a chýb merania, pričom obidve chyby sú súčtom veľkého počtu náhodných premenných, ktoré spôsobujú malé odchýlky endogénnej premennej od jej nenáhodnej časti. Rozdelenie takto definovaných náhodných porúch vyplýva z centrálnej limitnej vety, podľa ktorej rozdelenie súčtu náhodných premenných konverguje s rastom počtu členov súčtu k normálnemu rozdeleniu. Normalita rozdelenia náhodných porúch je východiskom pre štatistickú indukciu modelu (testovanie parametrov modelu aj modelu ako celku, intervalové odhady parametrov. . . ). 9

2. 2 Odhad parametrov lineárneho ekonometrického modelu s dvomi premennými Odhady parametrov lineárneho modelu (2. 1) budeme označovať . Hodnoty skutočných parametrov nepoznáme, ale na základe náhodného výberu dvojíc pozorovaní premenných Y, X je možné ich štatisticky odhadnúť v tvare výberovej regresnej priamky (2. 16) Rozdiel medzi skutočnou hodnotou endogénnej premennej Yi a vyrovnanou (ležiacou na priamke) , budeme označovať ei a nazývať reziduály: (2. 17) Pre odhad parametrov je zrejme najdôležitejšie vybrať kritérium pre odhad výberovej regresnej priamky. Od takejto priamky očakávame, že najlepšie vyrovná (vystihne) skutočnú závislosť medzi premennými Y a X , pričom by bolo želateľné, aby každá odchýlka v procese minimalizácie bola penalizovaná úmerne k jej veľkosti. Túto vlastnosť spĺňa metóda najmenších štvorcov založená na kritériu minimalizácie súčtu štvorcov odchýlok: 10

minimum (2. 18) Toto kritérium vyhovuje požiadavke, aby penalizácia väčších odchýlok bola prísnejšia ako u odchýlok menších. Ak napr. určitá odchýlka je päť krát väčšia ako iná, posudzuje sa až dvadsaťpäť krát prísnejšie. Úloha (2. 18) je z matematického hľadiska hľadanie voľného extrému funkcie : (2. 19) Extrém funkcie (2. 18) resp. (2. 19) obvykle riešime formuláciou podmienok existencie extrému: prvé parciálne derivácie podľa neznámych parametrov položíme rovné nule t. j. : (2. 20) 11

(2. 21) Úpravou sústavy (2. 21) získame tzv. normálne rovnice metódy najmenších štvorcov: (2. 22) Vydelením prvej rovnice počtom pozorovaní n dostaneme (2. 23) (2. 24) 12

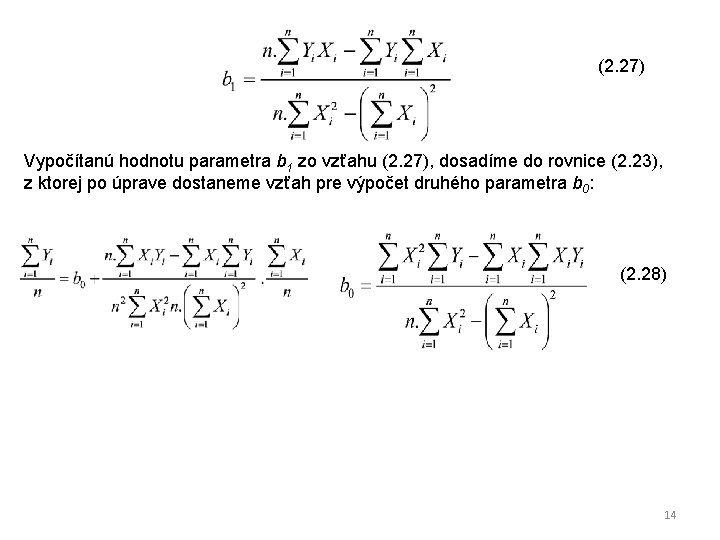
To znamená, že regresná priamka prechádza bodom so súradnicami rovnými priemerom premenných Y a X t. j. ( ). Riešením sústavy (2. 22) získame odhady parametrov lineárneho ekonometrického modelu tak, že vynásobíme prvú rovnicu a druhú rovnicu vynásobíme počtom pozorovaní n (2. 25) a odpočítame prvú rovnicu od druhej: (2. 26) Zo vzťahu (2. 26) po úprave dostaneme: 13

(2. 27) Vypočítanú hodnotu parametra b 1 zo vzťahu (2. 27), dosadíme do rovnice (2. 23), z ktorej po úprave dostaneme vzťah pre výpočet druhého parametra b 0: (2. 28) 14

2. 3 Štatistické vlastnosti odhadovej funkcie najmenších štvorcov Bodové odhady parametrov, ktoré sme získali vyššie popísaným spôsobom, sú lineárnymi funkciami pozorovaní náhodnej endogénnej premennej Y a pozorovaní fixnej exogénnej premennej X. Odhadnutá regresná priamka je len jednou z mnohých priamok, ktorými je možné preložiť korelačné pole údajov (Xi, Yi) kde i = 1, 2, . . . , n. Výsledkom metódy najmenších štvorcov sú estimátory parametrov lineárnej regresnej funkcie vo forme bodových odhadov , ktoré sa môžu od skutočných hodnôt líšiť. Je preto potrebné overiť, či estimátory majú požadované vlastnosti, ktoré musia spĺňať. Pripomeňme si niektoré základné teoretické požiadavky štatistickej indukcie o vlastnostiach estimátorov. Predpokladajme, že odhadujeme neznámy parameter z výberového súboru údajov a označme jeho hodnotu 15

Pri posudzovaní vlastností estimátorov sa najčastejšie využívajú tieto charakteristiky: • Stredná hodnota • Rozptyl • Výberová chyba = , vyjadruje rozdiel medzi skutočnou hodnotou parametra a jej odhadom. • Skreslenie, t. j. rozdiel medzi strednou hodnotou estimátora a skutočnou hodnotou parametra: • Stredná štvorcová chyba MSE (Mean Square Error), ktorá meria rozptyl estimátora okolo skutočnej hodnoty parametra: Aby mohli byť estimátory využiteľné v ekonometrickej analýze ekonomických javov musia spĺňať určité požadované štatistické vlastnosti: • neskreslenosť (nestrannosť, nevychýlenosť) • výdatnosť, efektívnosť • konzistentnosť • asymptotická neskreslenosť • asymptotická výdatnosť 16

Neskreslenosť je základnou požiadavkou bodových odhadov, vyjadrujúcou vlastnosť, kedy stredná hodnota odhadovaného parametra sa rovná skutočnej hodnote parametra: resp. pre parametre lineárneho modelu Niekedy sa neskreslenosť označuje ako odhad bez systematickej chyby, kedy odhad nepodhodnocujeme ani nenadhodnocujeme. Naopak skreslené odhady sú zaťažené systematickou chybou. Samotná vlastnosť však ešte nezaručuje, že neskreslený odhad je dobrý. Je preto žiaduce, aby sme okrem skreslenosti posudzovali aj jeho rozptyl, lebo často neskreslený estimátor môže mať taký veľký rozptyl, že konkrétny odhad je príliš vzdialený od skutočnej hodnoty. Dokonca estimátor s malým skreslením a veľmi malým rozptylom by sme niekedy preferovali. 17

Výdatnosť (efektívnosť) estimátora nazývame vlastnosť, kedy jeho rozptyl je menší alebo rovnaký, ako rozptyl akéhokoľvek iného neskresleného estimátora. Označme ľubovoľný nestranný estimátor , potom je výdatný estimátor ak platí: resp. pre parametre lineárneho modelu je možné ich variabilitu určiť: 18

Rozptyly estimátorov b 0 a b 1 sú priamo úmerné rozptylu náhodných porúch a nepriamoúmerné sume štvorcov odchýlok exogénnej premennej Xi ad jej priemeru. Znamená to, že čím je menší rozptyl náhodných porúch, tým presnejšie budú odhady parametrov, naopak čím väčšia bude variabilita exogénnej premennej, tým presnejšie odhadneme parametre modelu. Konzistentnosť je vlastnosť estimátora, kedy požadujeme aby s rastom pozorovaní , platilo pre pravdepodobnosť, že odhad sa od skutočného parametra bude líšiť, konverguje k nule, resp. pravdepodobnosť, že odhad sa od skutočného parametra líšiť nebude, konverguje k jednej. Inými slovami estimátor je konzistentný, ak jeho rozdelenie pravdepodobnosti s rastom veľkosti výberového súboru sa degeneruje do jedného bodu, ktorým je skutočný parameter. Asymptotická neskreslenosť, je vlastnosť estimátora, kedy s rastom výberu konverguje jeho stredná hodnota k skutočnému parametru t. j. platí: Ak je parameter neskreslený, je aj asymptoticky neskreslený, naopak to platiť nemusí. 19

Asymptoticky výdatný je estimátor ak je konzistentný, jeho asymptotické rozdelenie pravdepodobnosti má konečnú strednú hodnotu a konečný rozptyl a neexistuje žiadny iný konzistentný estimátor, ktorý má menší asymptotický rozptyl ako tento estimátor. Ak využijeme podobnú symboliku ako pri výdatnosti, musí platiť: Lineárny regresný model má okrem parametrov aj ďalší neznámi parameter – rozptyl náhodných porúch Pri jeho výpočte vyjdeme z odpočítania spriemerovanej rovnice (2. 24) od pôvodnej rovnice (2. 8), pričom po úprave dostaneme: (2. 29) ak platí: (2. 30) (2. 31) vypočítame strednú hodnotu súčtu štvorcov reziduálov z tvaru (2. 31) a po úprave dostaneme: 20

Na základe tohto postupu je možné odvodiť odhad rozptylu náhodných porúch pomocou neskresleného estimátora s 2 : (2. 32) 21

a odhady rozptylov parametrov: (2. 33) PRÍLOHA K PREDNÁŠKE 2: Príklad 2. 1 22

Otázky k 2. PREDNÁŠKE 1. Uveďte stručne definíciu klasických predpokladov lineárneho ekonometrického modelu. 2. Popíšte problémy nesplnenia predpokladov lineárneho ekonometrického modelu. 3. Charakterizujte odhad parametrov lineárneho ekonometrického modelu metódou najmenších štvorcov. 4. Formulujte štatistické vlastnosti odhadovej funkcie najmenších štvorcov. 5. Ktoré charakteristiky sa najčastejšie používajú pri posudzovaní vlastností estimátorov najmenších štvorcov. 6. Aké vlastnosti musia spĺňať estimátory aby boli použiteľné v ekonometrickej analýze ekonomických javov. 7. Charakterizujte neskreslenosť. 8. Charakterizujte výdatnosť. 9. Charakterizujte konzistentnosť. 10. Dokážte, že štvorcová chyba estimátora je súčtom jeho rozptylu a štvorca jeho skreslenia. 23