Ekonometria stosowana Heteroskedastyczno skadnika losowego Piotr Cikowicz Katedra

Ekonometria stosowana Heteroskedastyczność składnika losowego Piotr Ciżkowicz Katedra Międzynarodowych Studiów Porównawczych

Heteroskedastyczność składnika losowego ► Heteroskedastyczność jest naruszeniem kolejnego założenia MNK tzn. stałości wariancji składnika losowego między okresami (w przypadku szeregu czasowego) lub jednostkami (w przypadku danych przekrojowych) ► Oznacza to, że macierz wariancji i kowariancji składnika losowego może mieć postać np. jeśli wariancja przyjmuje dwie różne wartości dla dwóch podprób

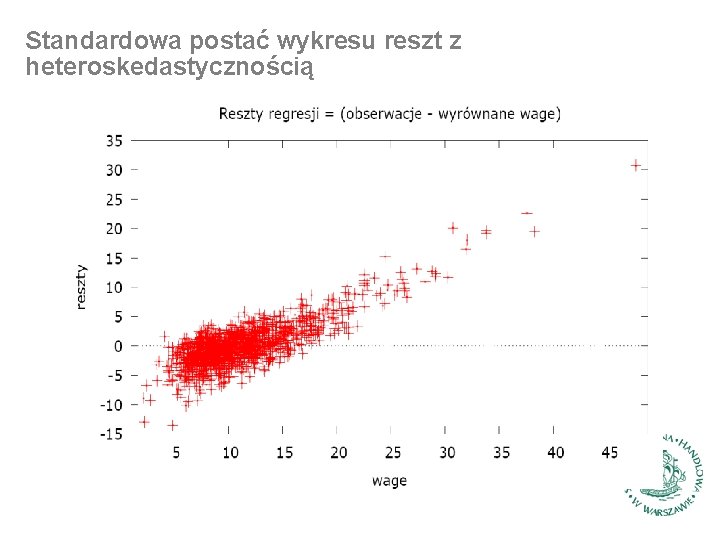
Standardowa postać wykresu reszt z heteroskedastycznością

Konsekwencje heteroskedastyczności składnika losowego ► Podobnie jak w przypadku autokorelacji tzn. ► estymator MNK pozostaje estymatorem nieobciążonym, bo nadal zachodzi… ► estymator MNK przestaje być najefektywniejszy ► estymator wariancji składnika losowego jest obciążony, co oznacza, że (zwykle) niedoszacowane są średnie błędy estymatorów parametrów (przeszacowane statystyki t ) oraz przeszacowany jest współczynnik determinacji

Testowanie heteroskedastyczności – test White’a ► Testowany jest następujący zestaw hipotez: ► Procedura testowa: ► Krok 1: estymujemy model MNK ► Krok 2: estymujemy model pomocniczy postaci (dla dwóch zmiennych objaśniających): ► Krok 3: testujemy zestaw hipotez ► Przy prawdziwości hipotezy zerowej (homoskedastyczność) statystyk testowa postaci T*R^2 ma rozkład Chi-kwadrat z liczbą stopni swobody równą liczbie restrykcji w hipotezie

Estymacja MNK w przypadku heteroskedastyczności ► Postać ogólna macierzy kowariancji estymatora: ► Postać macierzy kowariancji dla estymatora FGLS (feasible generalized least squares) lub EGLS (od estimated):

Estymacja MNK w przypadku heteroskedastyczności ► W praktyce nie znamy macierzy transformacji, ale niekiedy możemy zakładać jej postać np. : ► Estymator UMNK otrzymujemy dokonując regresji MNK na przetransformowanym modelu postaci:

Estymacja MNK w przypadku heteroskedastyczności ► Otrzymany w efekcie estymator nosi nazwę ważonego estymatora MNK i przybiera postać ► W efekcie obserwacje z większą wariancją otrzymują mniejszą wagę tzn. większe „znaczenie” jest przypisywane tym obserwacjom, które dostarczają bardziej precyzyjnej informacji o parametrach modelu ► Macierz kowariancji estymatora jest dana wzorem

Estymacja MNK w przypadku heteroskedastyczności ► W praktyce nie znamy jednak wartości h(i), stąd zazwyczaj stosuje się dwa podejścia: ► estymacja MNK na przeskalowanych zmiennych ► estymacja h(i) jako funkcji zmiennych objaśniających ► W drugim przypadku stosuje się często podejście bazujące na założeniu, że heteroskedastyczność jest multiplikatywna tzn. gdzie z jest wektorem zmiennych obserwowalnych, zazwyczaj podzbiorem zmiennych objaśniających wyjściowego modelu.

Estymacja MNK w przypadku heteroskedastyczności ► Estymacja EGLS w przypadku tak zdefiniowanej heteroskedastyczności wygląda następująco: ► estymujemy podstawowy model metodą MNK ► obliczamy logarytmy kwadratów reszt z tego modelu ► estymujemy wartości parametrów stojących przy wektorze zmiennych z na podstawie regresji: ► obliczamy i dokonujemy transformacji obserwacji wyjściowych tzn. : ► przeprowadzamy regresję na tak zdefiniowanych zmiennych korzystając z MNK, gdzie postać estymatora to:

Estymacja MNK w przypadku heteroskedastyczności ► W tak otrzymanym modelu zgodnym estymatorem wariancji składnika losowego jest ► Zaś zgodnym estymatorem macierzy kowariancji parametrów strukturalnych jest

Heteroscedasticity- consistent standard errors (błędy White’a lub błędy HA) ► Na podstawie macierz kowariancji można zapisać też jako: ► White (1980) pokazał, że do estymacji tej macierzy potrzebny jest jedynie zgodny estymator macierzy

Heteroscedasticity- consistent standard errors (błędy White’a lub błędy HA) ► Przy dość ogólnych założeniach zgodnym estymatorem powyższej macierzy jest co pozwala na estymację „prawdziwej” macierzy kowariancji estymatora OLS ► Na tej postawie można wyznaczyć zgodne błędy szacunku

Heteroscedasticity-and-autocorellation- consistent standard errors (błędy HAC lub błędy Neweya-Westa) ► Podejście HA jest szczególnym przypadkiem estymacji błędów HAC postaci: gdzie ► Dla w(j)=0 otrzymujemy błędy HA. Przy autokorelacji najczęściej stosuje się wago Bartletta postaci ► Intuicyjnie oddają one fakt, że zazwyczaj autokorelacja maleje wraz z rzędem opóźnienia j.