ECE 6382 Fall 2019 David R Jackson Notes

ECE 6382 Fall 2019 David R. Jackson Notes 22 Bessel Function Examples Note: j is used in this set of notes instead of i. 1

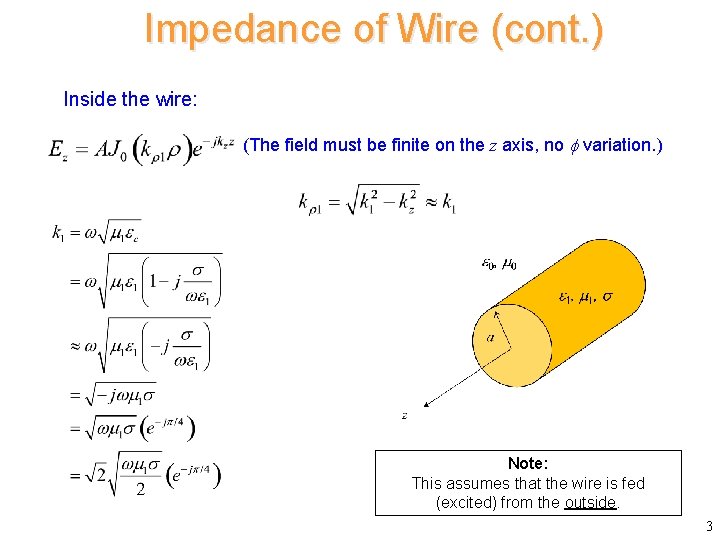
Impedance of Wire A round wire made of conducting material is examined. 0 , 0 1 , a z The wire has a conductivity of . We neglect the z variation of the fields inside the wire (|kz| << |k 1|). 2

Impedance of Wire (cont. ) Inside the wire: (The field must be finite on the z axis, no variation. ) Note: This assumes that the wire is fed (excited) from the outside. 3

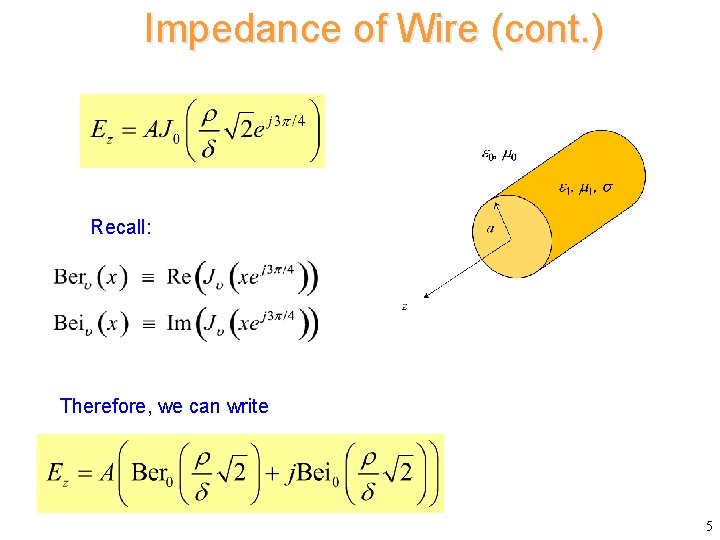
Impedance of Wire (cont. ) Hence, we have where (skin depth) We can also write the field as (J 0 is an even function. ) 4

Impedance of Wire (cont. ) Recall: Therefore, we can write 5

Impedance of Wire (cont. ) The current flowing in the wire is Hence 6

Impedance of Wire (cont. ) The impedance per unit length defined as: Hence, Note: This assumes that the wire is fed (excited) from the outside. 7

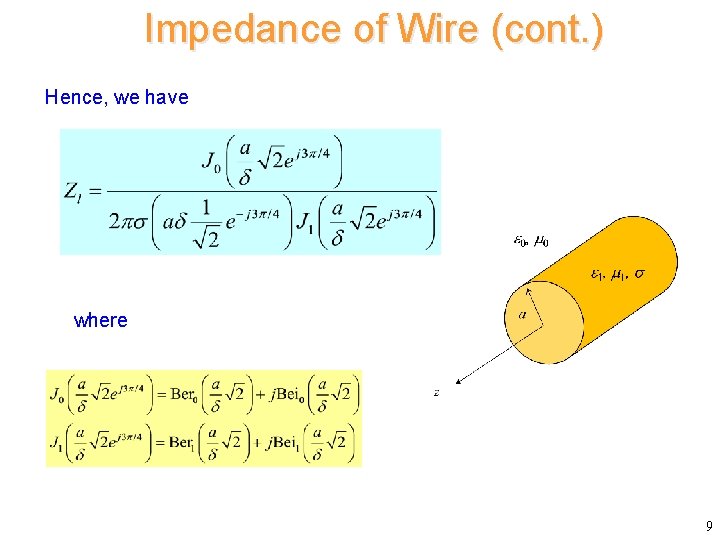
Impedance of Wire (cont. ) We have the following helpful integration identity: Hence where 8

Impedance of Wire (cont. ) Hence, we have where 9

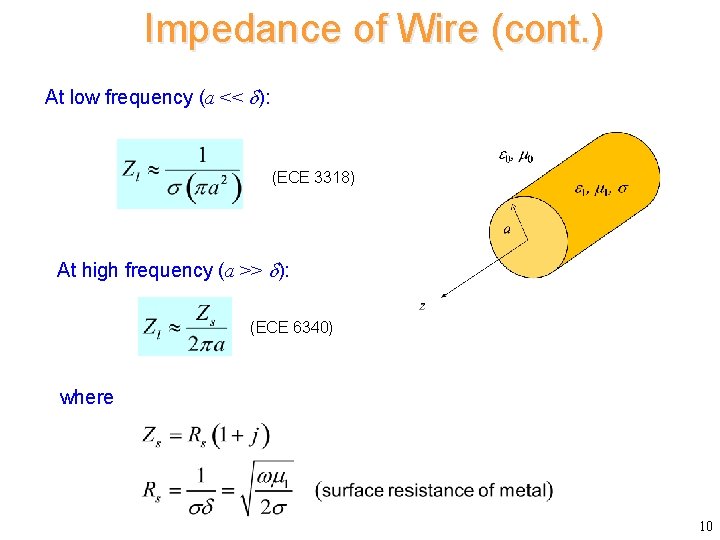
Impedance of Wire (cont. ) At low frequency (a << ): (ECE 3318) At high frequency (a >> ): (ECE 6340) where 10

Circular Waveguide The waveguide is homogeneously filled, so we have independent TEz and TMz modes. TMz mode: a r z Note: The relative permittivity could be complex (due to loss). 11

Circular Waveguide (cont. ) (1) variation (uniqueness of solution) Choose 12

Circular Waveguide (cont. ) (2) The field should be finite on the z axis is not allowed 13

Circular Waveguide (cont. ) (3) B. C. ’s: Hence 14

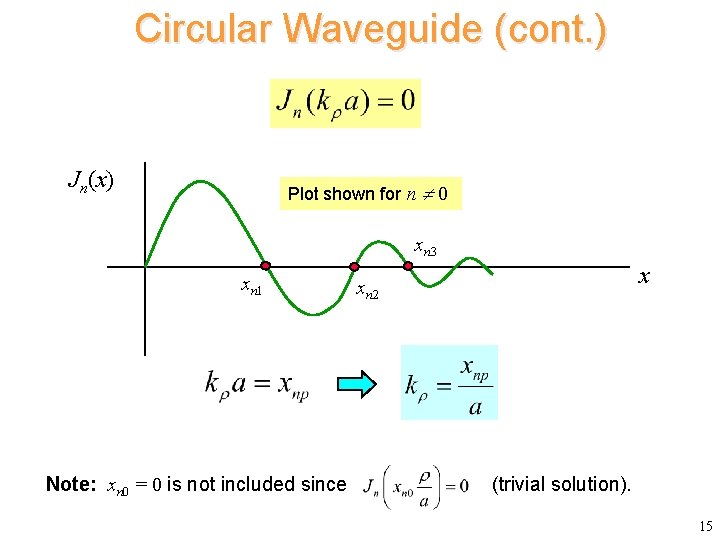
Circular Waveguide (cont. ) Jn(x) Plot shown for n 0 xn 3 xn 1 Note: xn 0 = 0 is not included since x xn 2 (trivial solution). 15

Circular Waveguide (cont. ) TMnp mode: 16

Cutoff Frequency: TMz (We assume a lossless dielectric for the cutoff discussion. ) 17

Cutoff Frequency: TMz (cont. ) xnp values pn 0 1 2 3 4 5 1 2. 405 3. 832 5. 136 6. 380 7. 588 8. 771 2 5. 520 7. 016 8. 417 9. 761 11. 065 12. 339 3 8. 654 10. 173 11. 620 13. 015 14. 372 4 11. 792 13. 324 14. 796 TM 01, TM 11, TM 21, TM 02, … 18

TEz Modes In this case the boundary condition is different: 19

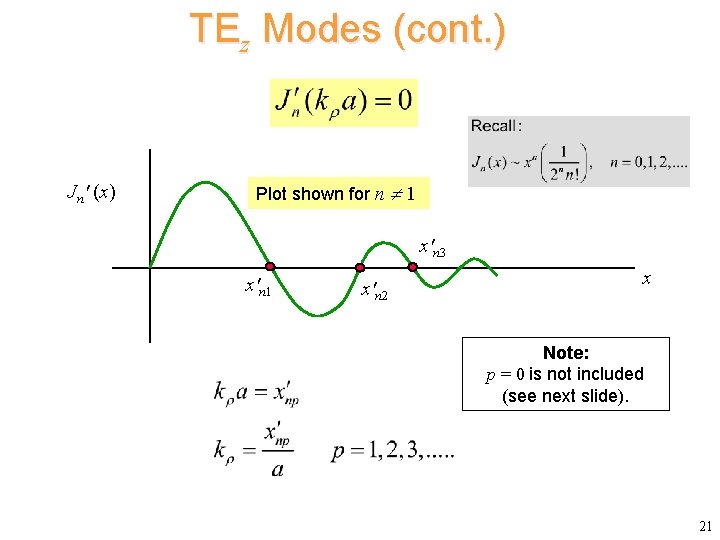
TEz Modes (cont. ) Set At he boundary, the first term on the RHS is zero: Hence 20

TEz Modes (cont. ) Jn' (x) Plot shown for n 1 x'n 3 x'n 1 x'n 2 x Note: p = 0 is not included (see next slide). 21

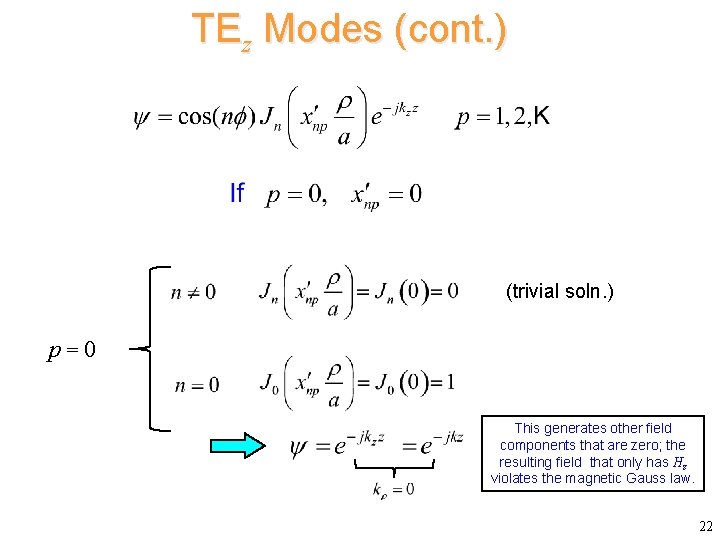
TEz Modes (cont. ) (trivial soln. ) p=0 This generates other field components that are zero; the resulting field that only has Hz violates the magnetic Gauss law. 22

Cutoff Frequency: TEz (We assume a lossless dielectric for the cutoff discussion. ) 23

Cutoff Frequency: TEz x´np values pn 0 1 2 3 4 5 1 3. 832 1. 841 3. 054 4. 201 5. 317 5. 416 2 7. 016 5. 331 6. 706 8. 015 9. 282 10. 520 3 10. 173 8. 536 9. 969 11. 346 12. 682 13. 987 4 13. 324 11. 706 13. 170 TE 11, TE 21, TE 01, TE 31, ……. . 24

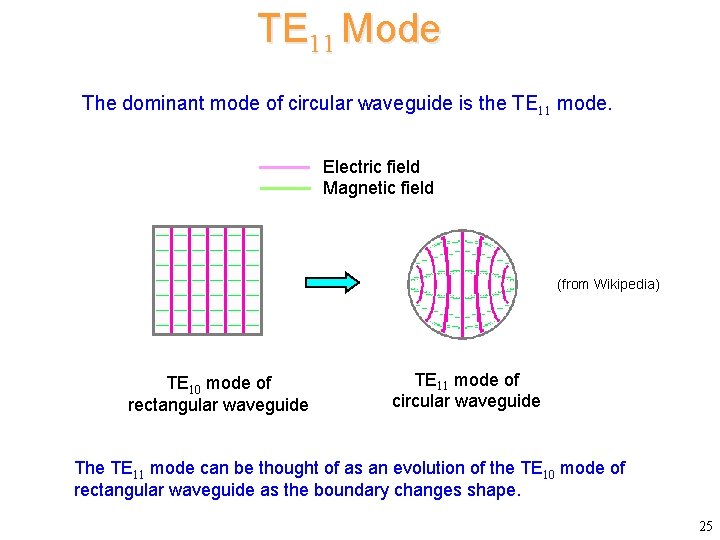
TE 11 Mode The dominant mode of circular waveguide is the TE 11 mode. Electric field Magnetic field (from Wikipedia) TE 10 mode of rectangular waveguide TE 11 mode of circular waveguide The TE 11 mode can be thought of as an evolution of the TE 10 mode of rectangular waveguide as the boundary changes shape. 25

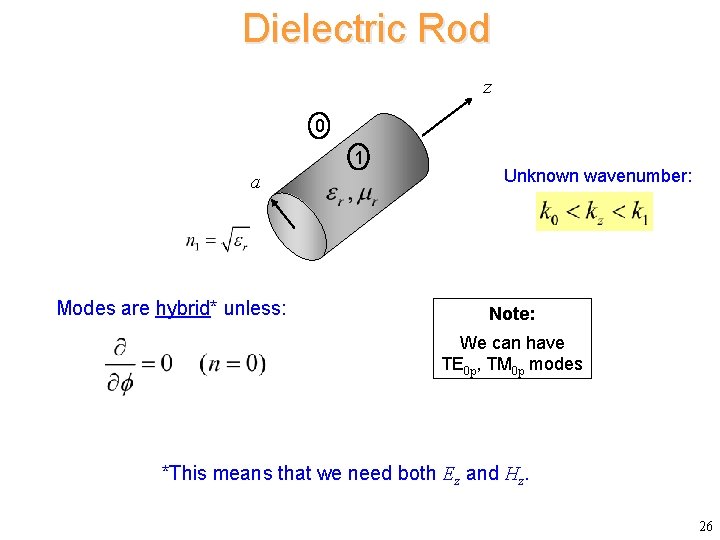
Dielectric Rod z 0 1 a Modes are hybrid* unless: Unknown wavenumber: Note: We can have TE 0 p, TM 0 p modes *This means that we need both Ez and Hz. 26

Dielectric Rod (cont. ) <a Representation of potentials inside the rod: where (kz is unknown) 27

Dielectric Rod (cont. ) To see choice of sin/cos, examine the field components (for example E ): From the Appendix: 28

Dielectric Rod (cont. ) >a Representation of potentials outside the rod: Use where Note: 0 is interpreted as a positive real number in order to have decay radially in the air region. 29

Dielectric Rod (cont. ) Useful identity: Another useful identity: Kn (x) = modified Bessel function of the second kind. 30

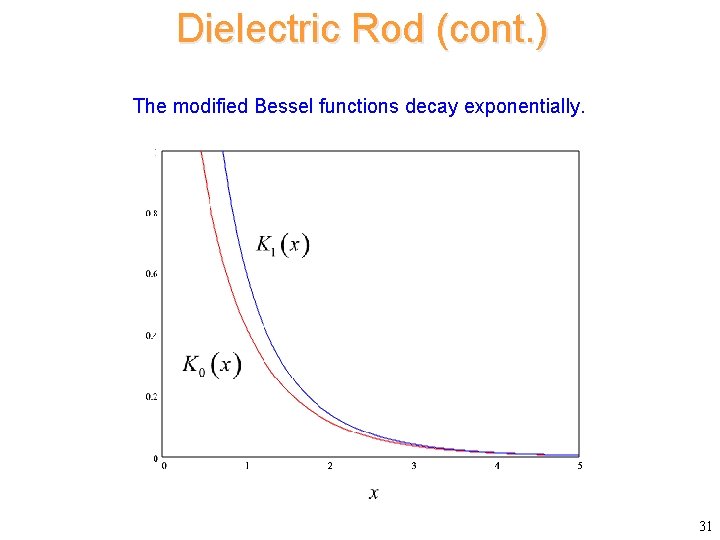
Dielectric Rod (cont. ) The modified Bessel functions decay exponentially. 31

Dielectric Rod (cont. ) Hence, we choose the following forms in the air region ( > a): 32

Dielectric Rod (cont. ) Match Ez , Hz , E , H at = a: Example: or so 33

Dielectric Rod (cont. ) To have a non-trivial solution, we require that kz = unknown (for a given frequency ) 34

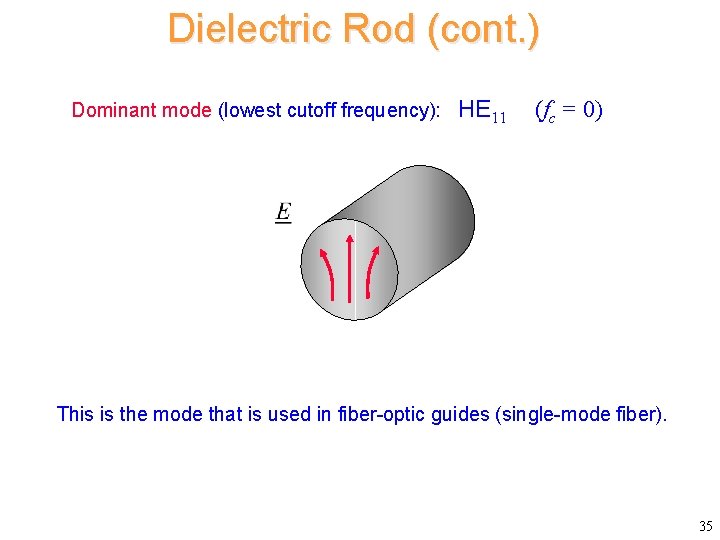
Dielectric Rod (cont. ) Dominant mode (lowest cutoff frequency): HE 11 (fc = 0) This is the mode that is used in fiber-optic guides (single-mode fiber). 35

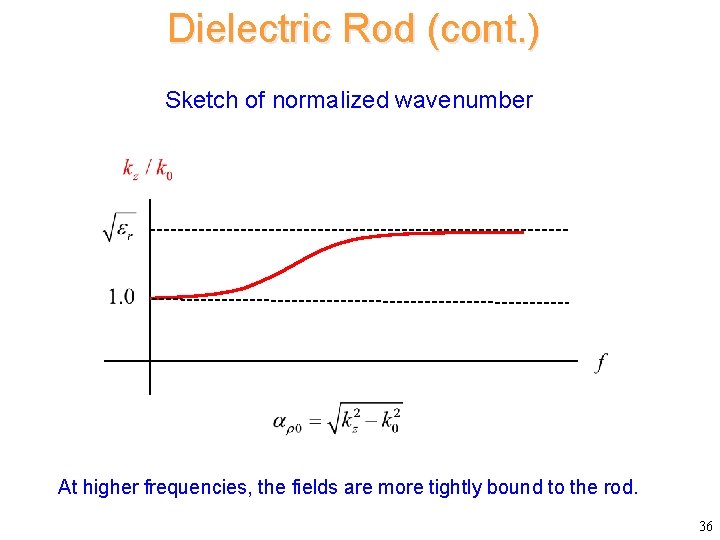
Dielectric Rod (cont. ) Sketch of normalized wavenumber At higher frequencies, the fields are more tightly bound to the rod. 36

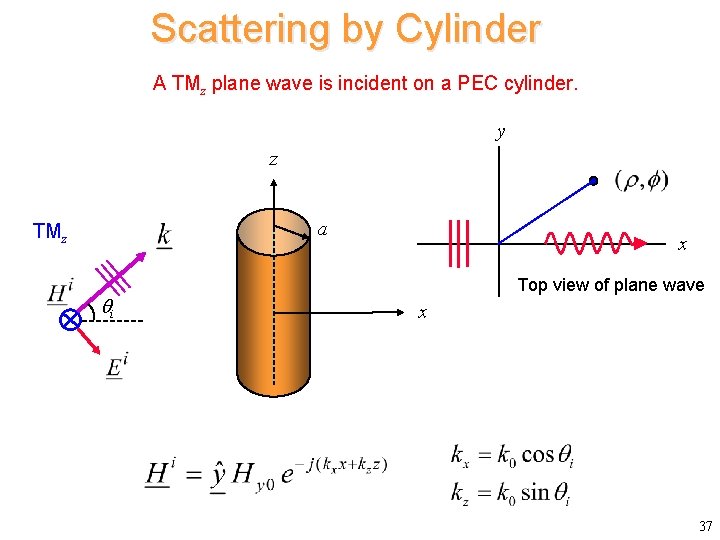
Scattering by Cylinder A TMz plane wave is incident on a PEC cylinder. y z a TMz qi x Top view of plane wave x 37

Scattering by Cylinder (cont. ) From the plane-wave properties, we have The total field is written as the sum of incident and scattered parts: For a: Note: For any wave of the form exp(-jkzz), all field components can be put in terms of Ez and Hz. This is why it is convenient to work with Ez. Please see the Appendix. 38

Scattering by Cylinder (cont. ) We first put into cylindrical form using the Jacobi-Anger identity*: where Assume the following form for the scattered field: *This was derived previously using the generating function. 39

Scattering by Cylinder (cont. ) At Hence This yields or 40

Scattering by Cylinder (cont. ) We then have and The other components of the scattered field can be found from the formulas in the Appendix. 41

Current Line Source z TMz : Conditions: 1) Allowed angles: 2) Symmetry: 3) Radiation condition: 4) Symmetry: Hence: 42

Current Line Source (cont. ) Our goal is to solve for the constant A: z I 0 Choose a small circular path: C 43

Current Line Source (cont. ) From Ampere’s law and Stokes’ theorem: z I 0 C Examine the last term (displacement current): where 44

Current Line Source (cont. ) Hence so Therefore Now use 45

Current Line Source (cont. ) Hence z or I 0 so C Thus This is the EM Green’s function for the field Ez due to a line source. 46

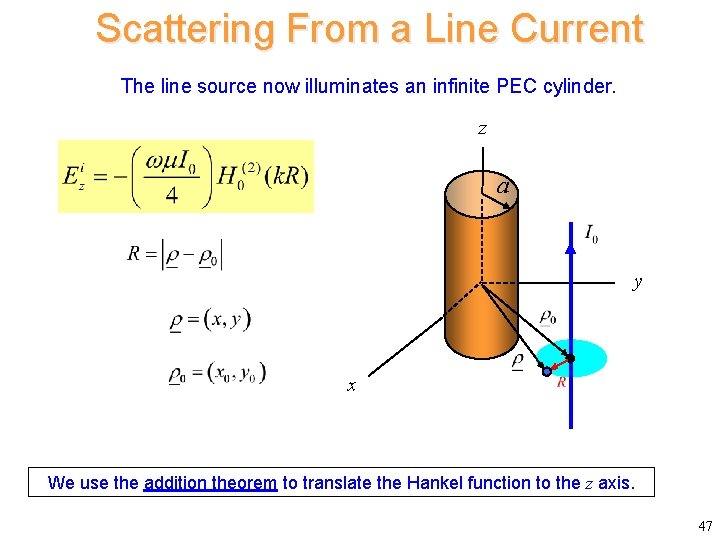
Scattering From a Line Current The line source now illuminates an infinite PEC cylinder. z a y x We use the addition theorem to translate the Hankel function to the z axis. 47

Scattering From a Line Current (cont. ) The addition theorem tells us: We use the first form, since the cylinder at = a is inside the circle on which the line source resides (radius 0). 48

Scattering From a Line Current (cont. ) Incident field: Assume a form for the scattered field: 49

Scattering From a Line Current (cont. ) Boundary Conditions ( = a): Hence or 50

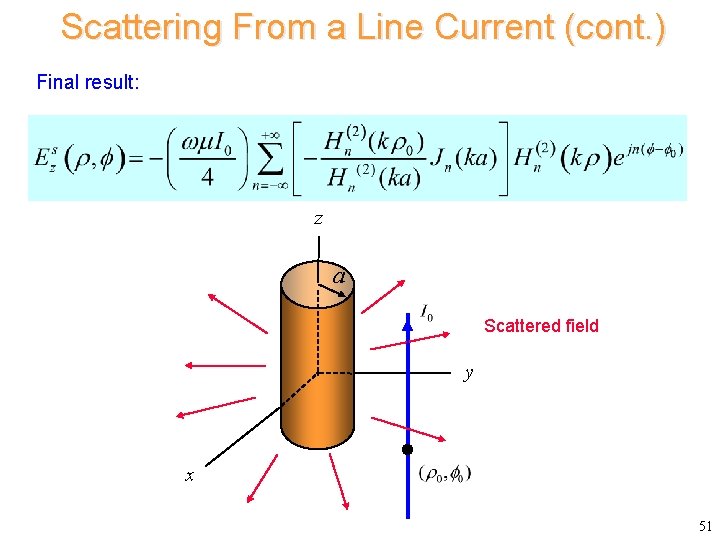
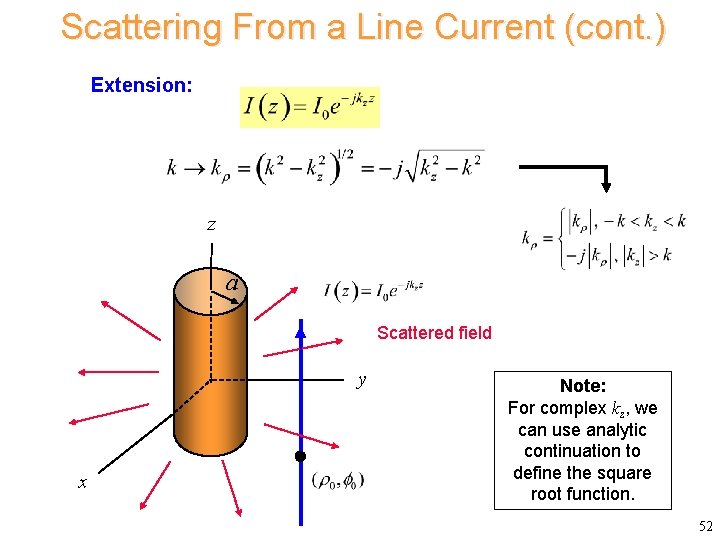
Scattering From a Line Current (cont. ) Final result: z a Scattered field y x 51

Scattering From a Line Current (cont. ) Extension: z a Scattered field y x Note: For complex kz, we can use analytic continuation to define the square root function. 52

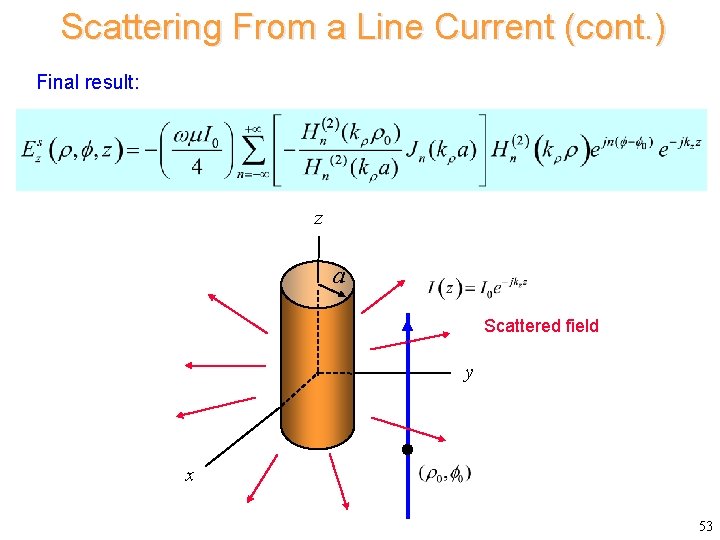
Scattering From a Line Current (cont. ) Final result: z a Scattered field y x 53

Appendix For any wave of the form exp(-jkz z), all field components can be put in terms of Ez and Hz. 54

Appendix (cont. ) These may be written more compactly as where 55

Appendix (cont. ) In cylindrical coordinates we have This allows us to calculate the field components in terms of Ez and Hz in cylindrical coordinates. 56

Appendix (cont. ) In cylindrical coordinates we then have 57