ECE 6382 Fall 2020 David R Jackson Notes

ECE 6382 Fall 2020 David R. Jackson Notes 15 The Steepest-Descent Method Notes are adapted from ECE 6341 1

Steepest-Descent Method Complex Integral: The method was published by Peter Debye in 1909. Debye noted in his work that the method was developed in a unpublished note by Bernhard Riemann (1863). Peter Joseph William Debye (March 24, 1884 – November 2, 1966) was a Dutch physicist and physical chemist, and Nobel laureate in Chemistry. Georg Friedrich Bernhard Riemann (September 17, 1826 – July 20, 1866) was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity. http: //en. wikipedia. org/wiki/Peter_Debye http: //en. wikipedia. org/wiki/Bernhard_Riemann 2

Steepest-Descent Method (cont. ) Complex Integral: We want to obtain an approximate evaluation of the integral when the real parameter Ω is very large. The functions f (z) and g(z) are analytic (except for poles or branch points), so that the path C may be deformed if necessary (possibly adding residue contributions or branch-cut integrals). Saddle Point (SP): (This is the point that ends up contributing the most. ) 3

Steepest-Descent Method (cont. ) Path deformation: If the path does not go through a saddle point, we assume that it can be deformed to do so. If any singularities are encountered during the path deformation, they must be accounted for (e. g. , residue of captured poles). X 4

Steepest-Descent Method (cont. ) Denote Cauchy Reimann eqs. : Hence Switch order 5

Steepest-Descent Method (cont. ) or If then Near the saddle point: (We can rotate coordinates to eliminate) 6

Steepest-Descent Method (cont. ) In the rotated coordinate system: Assume that the coordinate system is rotated so that Note: The angle of rotation necessary to do this will be clear later (it is the departure angle SDP of the steepest-descent path). 7

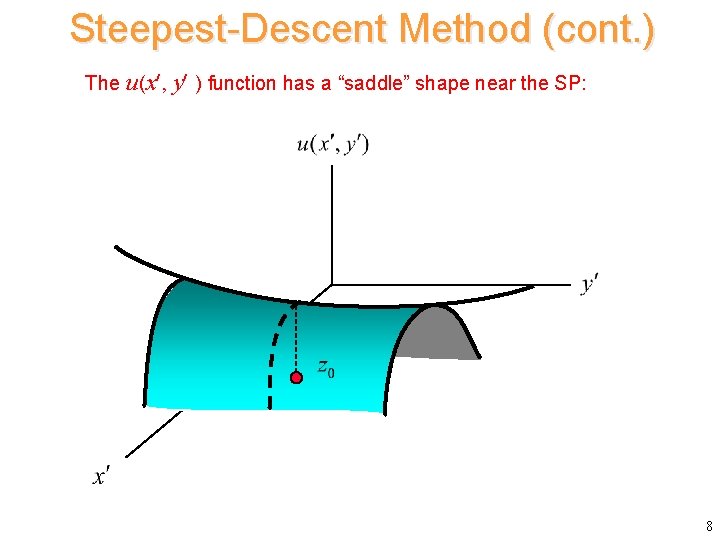
Steepest-Descent Method (cont. ) The u (x , y ) function has a “saddle” shape near the SP: 8

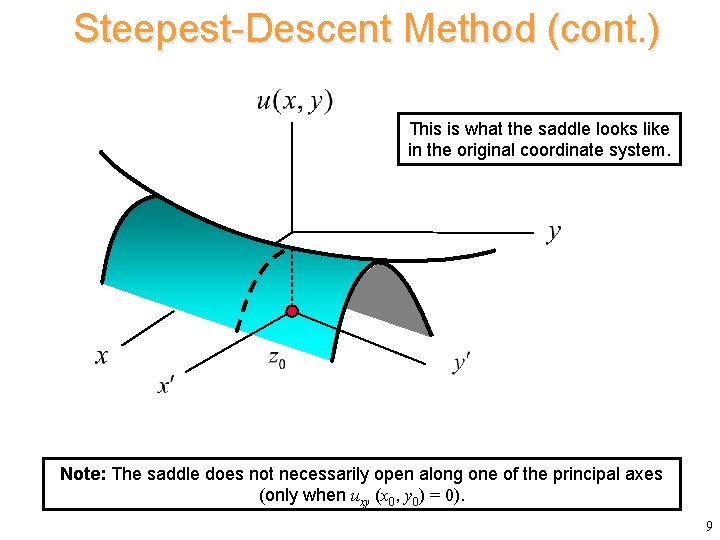
Steepest-Descent Method (cont. ) This is what the saddle looks like in the original coordinate system. Note: The saddle does not necessarily open along one of the principal axes (only when uxy (x 0, y 0) = 0). 9

Steepest-Descent Method (cont. ) A descending path is one on which the u function decreases away from the saddle point. 3 D view of a descending path 10

Steepest-Descent Method (cont. ) Along any descending path C we will have convergence: Exponentially decreasing function 11

Steepest-Descent Method (cont. ) Behavior on a Descending Path Note: The parameter s is related to the distance along the path from the saddle point. The convention is that negative s means before we get to the saddle point, positive s means after we leave the saddle point. When is large, most of contribution is from near z 0. 12

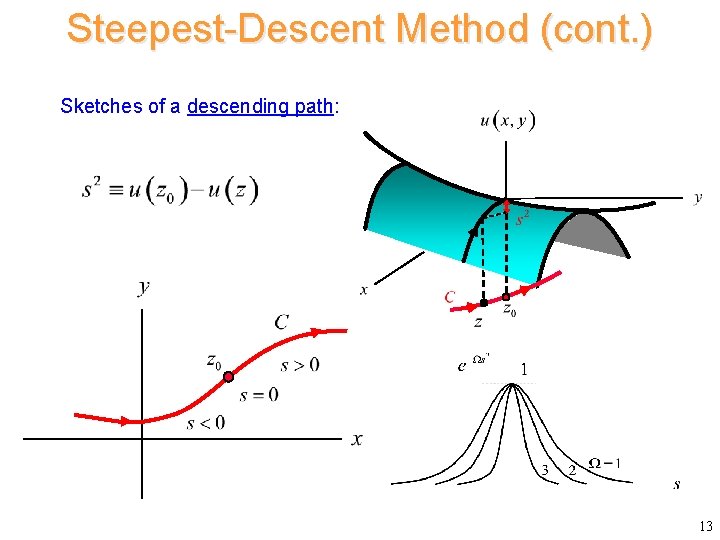
Steepest-Descent Method (cont. ) Sketches of a descending path: 13

Steepest-Descent Method (cont. ) Along any descending path: Both the phase and amplitude change along an arbitrary descending path C. Important Point: If we can find a path along which the phase does not change (v is constant), the integrand will have a purely exponentially decaying behavior (no phase term), making the integral easy to evaluate. 14

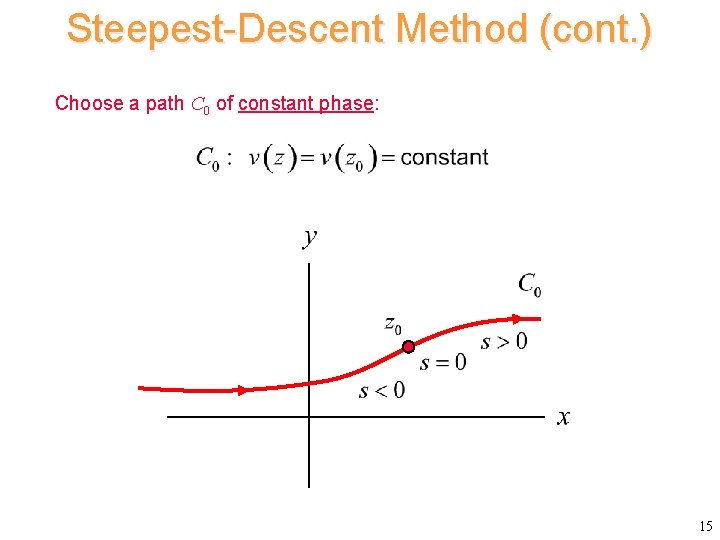
Steepest-Descent Method (cont. ) Choose a path C 0 of constant phase: 15

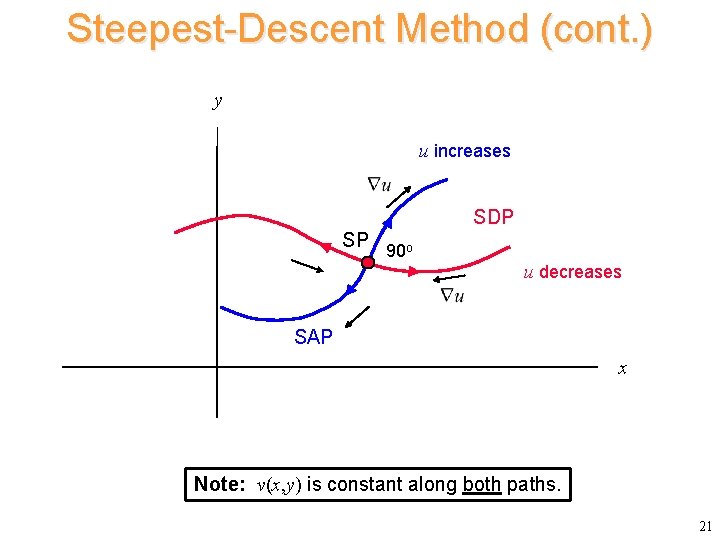
Steepest-Descent Method (cont. ) Gradient Property (proof on next slide): Hence C 0 is either a “path of steepest descent” (SDP) or a “path of steepest ascent” (SAP). SDP: u(x, y) decreases as fast as possible along the path away from the saddle point. SAP: u(x, y) increases as fast as possible along the path away from the saddle point. 16

Steepest-Descent Method (cont. ) Proof C. R. Equations y Hence, Also, C 0 x Hence 17

Steepest-Descent Method (cont. ) Because the v function is constant along the SDP, we have: or Real 18

Steepest-Descent Method (cont. ) Local behavior near SP so Denote 19

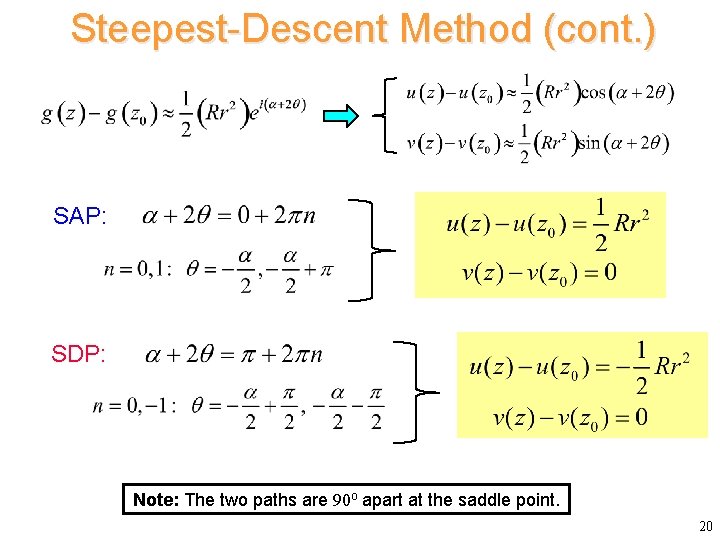
Steepest-Descent Method (cont. ) SAP: SDP: Note: The two paths are 90 o apart at the saddle point. 20

Steepest-Descent Method (cont. ) y u increases SDP SP 90 o u decreases SAP x Note: v(x, y) is constant along both paths. 21

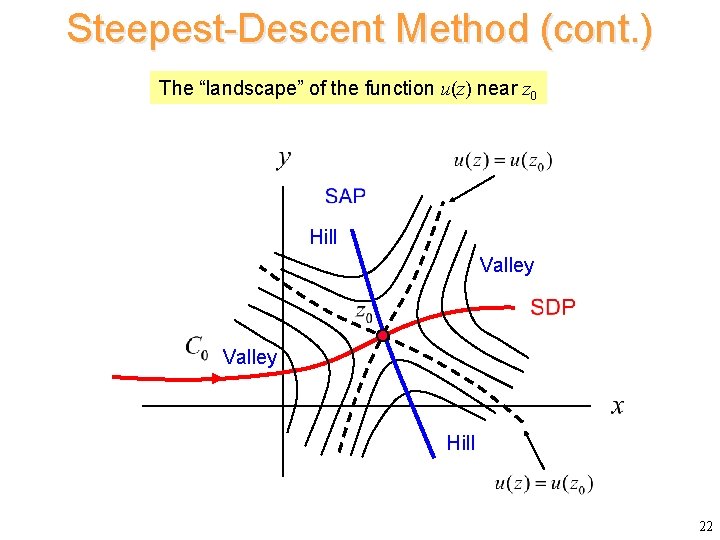
Steepest-Descent Method (cont. ) The “landscape” of the function u(z) near z 0 Hill Valley Hill 22

Steepest-Descent Method (cont. ) SAP SDP 23

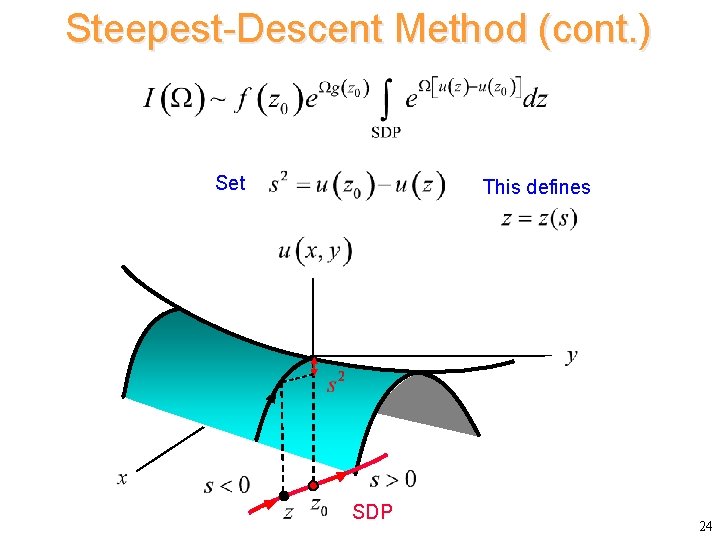
Steepest-Descent Method (cont. ) Set This defines SDP 24

Steepest-Descent Method (cont. ) We then have or (leading term of the asymptotic expansion) Hence 25

Steepest-Descent Method (cont. ) To evaluate the derivative: (Recall: v is constant along SDP. ) At the SP this gives 0 = 0. Take one more derivative: 26

Steepest-Descent Method (cont. ) At so Hence, we have 27

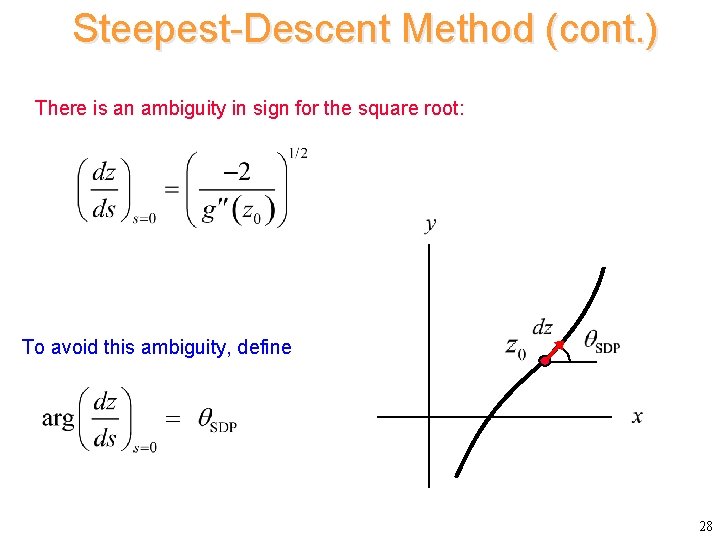
Steepest-Descent Method (cont. ) There is an ambiguity in sign for the square root: To avoid this ambiguity, define 28

Steepest-Descent Method (cont. ) The derivative term is therefore Hence 29

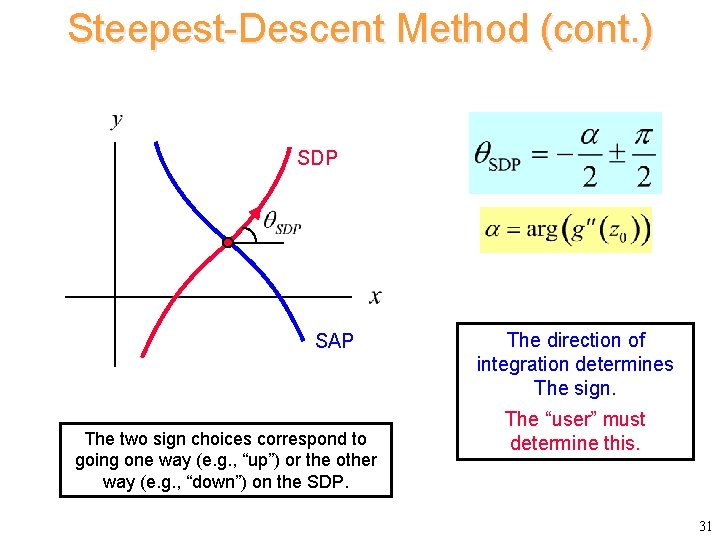
Steepest-Descent Method (cont. ) To find SDP : Denote 30

Steepest-Descent Method (cont. ) SDP SAP The two sign choices correspond to going one way (e. g. , “up”) or the other way (e. g. , “down”) on the SDP. The direction of integration determines The sign. The “user” must determine this. 31

Steepest-Descent Method (cont. ) Summary 32

Example where Hence, we identify: 33

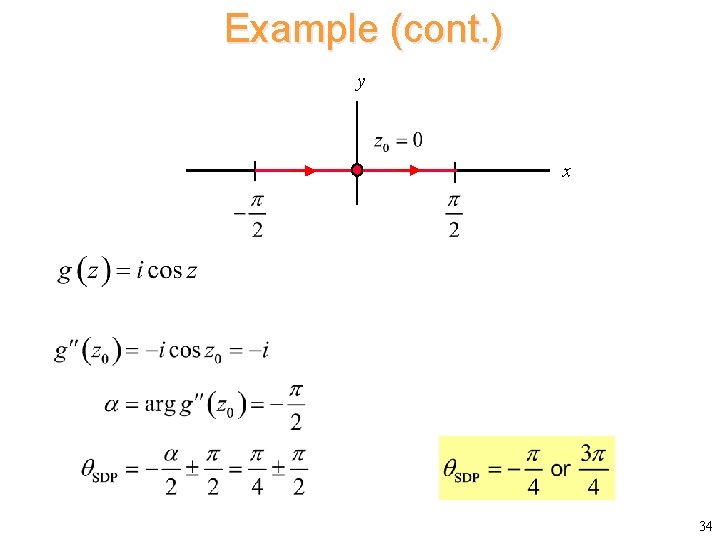
Example (cont. ) y x 34

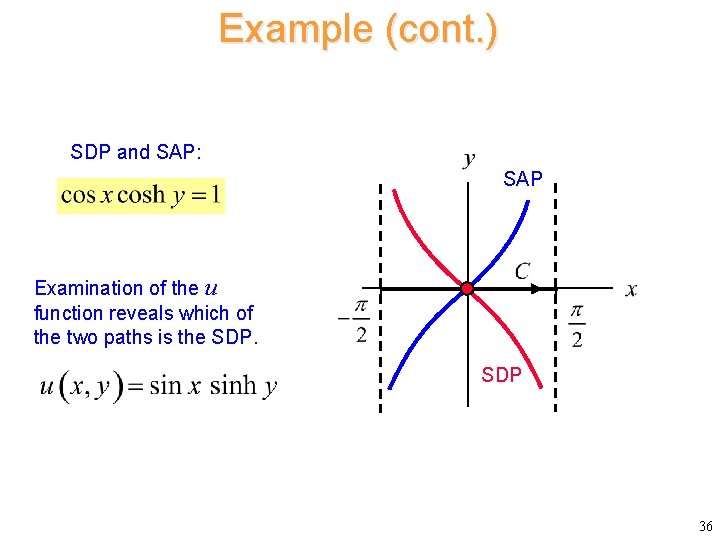
Example (cont. ) Identify the SDP and SAP: 35

Example (cont. ) SDP and SAP: SAP Examination of the u function reveals which of the two paths is the SDP 36

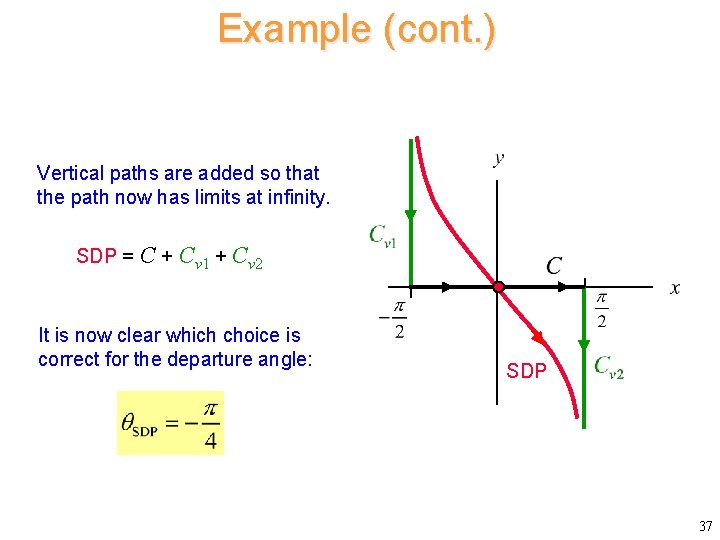
Example (cont. ) Vertical paths are added so that the path now has limits at infinity. SDP = C + Cv 1 + Cv 2 It is now clear which choice is correct for the departure angle: SDP 37

Example (cont. ) (If we ignore the contributions of the vertical paths. ) Hence, so 38

Example (cont. ) Hence 39

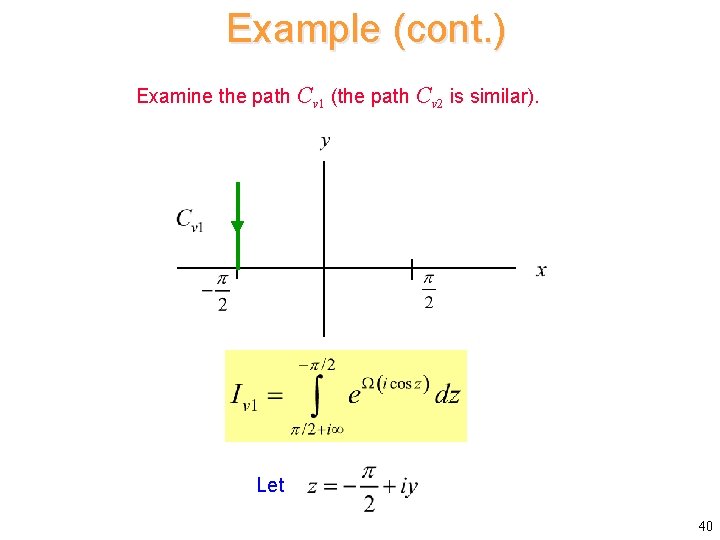
Example (cont. ) Examine the path Cv 1 (the path Cv 2 is similar). Let 40

Example (cont. ) since Since is becoming very large, we can write: Hence, we have 41

Example (cont. ) Hence, Iv 1 is a much smaller term than what we obtain from the method of steepest descent, when gets large, and we can ignore it. 42

Example The Gamma (generalized factorial) function: Note: There is no saddle point! Let 43

Example (cont. ) or 44

Example (cont. ) Recall the recipe: Note: The SDP is the positive real axis (see the derivation below). The departure angle is zero, not , since we are integrating from 0 to . Hence or This is Sterling’s formula (leading term). 45

Complete Asymptotic Expansion We can obtain the complete asymptotic expansion of the integral with the steepest-descent method (including as many higher-order terms as we wish). The path is along the SDP. Change of variables: Define: Then we have 46

Complete Asymptotic Expansion (cont. ) (Extending the limits to infinity gives an exponentially small error: This does not affect the asymptotic expansion. ) Assume Note: We can use an equal sign if h is analytic at s = 0, which is usually the case. Then Note: The integral is zero for n = odd (the integrand is then an odd function). This result is called “Watson’s Lemma”: We can obtain the complete asymptotic expansion of I by substituting in the complete asymptotic expansion for h and integrating term-by-term. 47

Complete Asymptotic Expansion (cont. ) Performing the integration, where We then have 48

Complete Asymptotic Expansion (cont. ) Summary where 49

Complete Asymptotic Expansion (cont. ) Note: Keeping only the leading term gives the usual steepest-descent result. where 50

Complete Asymptotic Expansion (cont. ) Example: We have SDP: y = 0 (real axis) SAP: x = 0 (imaginary axis) 51

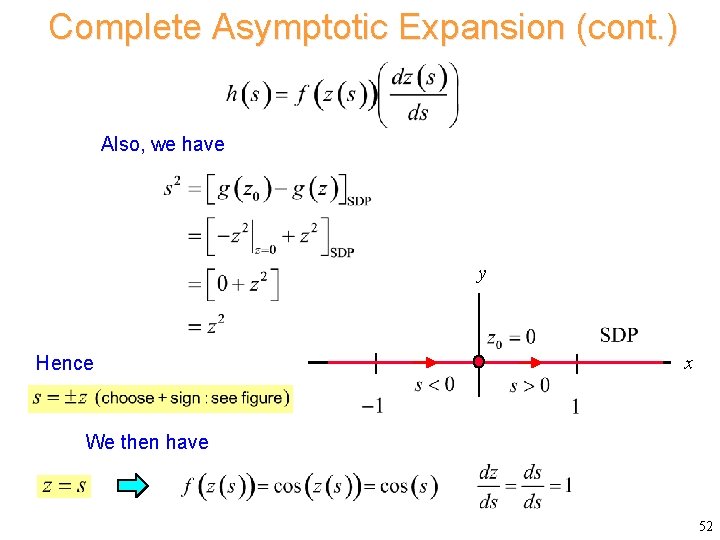
Complete Asymptotic Expansion (cont. ) Also, we have y Hence x We then have 52

Complete Asymptotic Expansion (cont. ) Hence Recall: 53

Complete Asymptotic Expansion (cont. ) The complete asymptotic expansion is Hence we have: so that where (Please see the notes on the Gamma function. ) 54

Complete Asymptotic Expansion (cont. ) Hence we have: as Note: In a similar manner, we could obtain higher-order terms in the asymptotic expansion of the Bessel function or the Gamma function. 55