ECE 6382 Fall 2020 David R Jackson Notes

ECE 6382 Fall 2020 David R. Jackson Notes 21 Modified Bessel Functions and Kelvin Functions Notes are from D. R. Wilton, Dept. of ECE 1

Modified Bessel Functions Modified Bessel differential equation: This comes from the Bessel differential equation: The modified Bessel functions are Bessel functions of imaginary argument. 2

Modified Bessel Function of the First Kind Definition: (I is a real function of x. ) To see this, use the Frobenius solution for J : Frobenius series solution for I : 3

Second Solution of Modified Bessel Equation For n, the modified Bessel function of the 2 nd kind is defined as: For = n (an integer): 4

Relations Between Bessel and Modified Bessel Functions The modified Bessel functions are related to the regular Bessel functions as Note: The added factors in front ensure that the functions are real. *comes from: 5

Small Argument Approximations For small arguments we have: 6

Large Argument Approximations For large arguments we have: 7

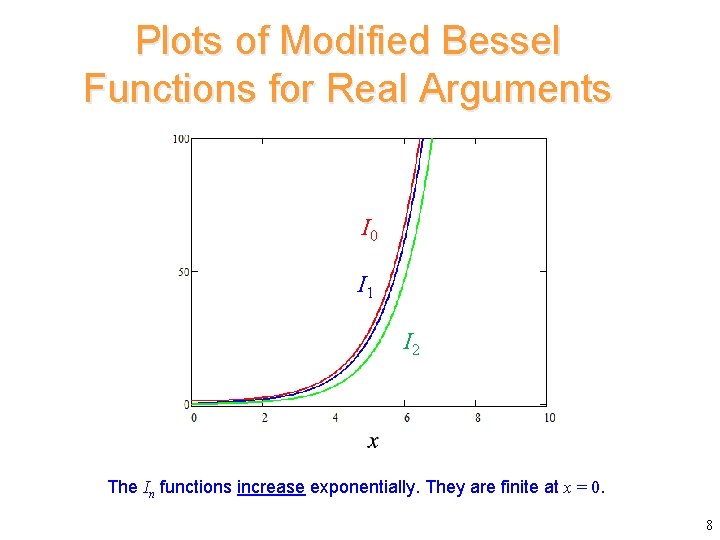
Plots of Modified Bessel Functions for Real Arguments I 0 I 1 I 2 The In functions increase exponentially. They are finite at x = 0. 8

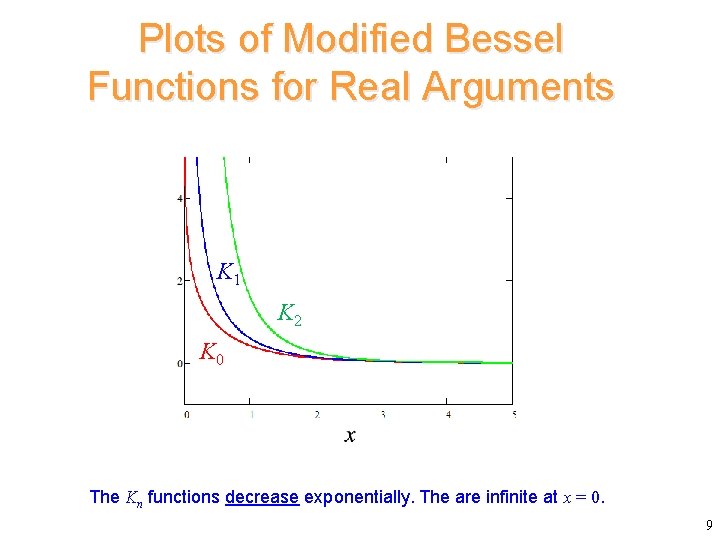
Plots of Modified Bessel Functions for Real Arguments K 1 K 2 K 0 The Kn functions decrease exponentially. The are infinite at x = 0. 9

Recurrence Relations Some recurrence relations are: 10

Wronskian A Wronskian identity is: 11

Kelvin Functions The Kelvin functions are defined as Note: These are important for studying the fields inside of a conducting wire. 12

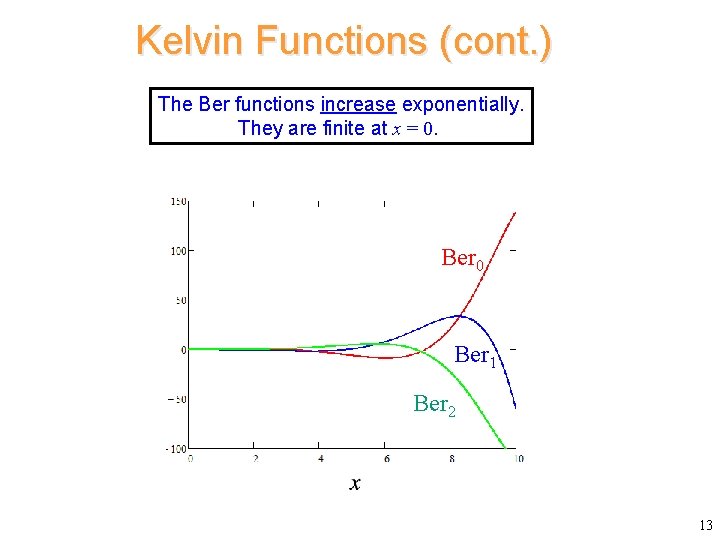
Kelvin Functions (cont. ) The Ber functions increase exponentially. They are finite at x = 0. Ber 0 Ber 1 Ber 2 13

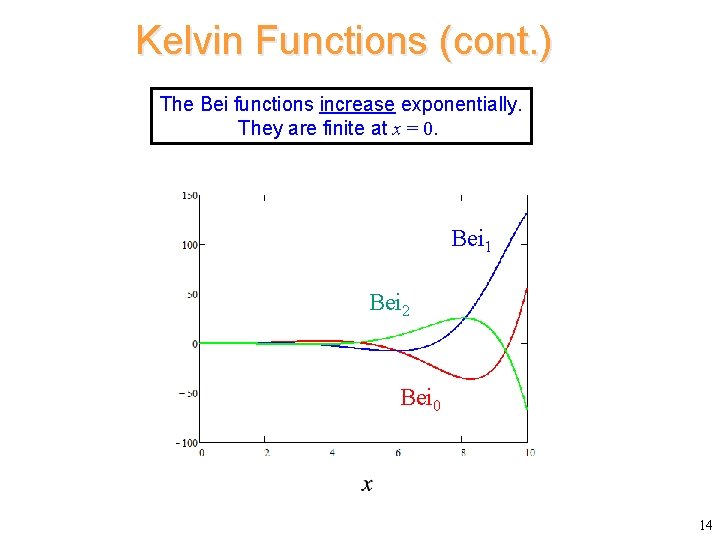
Kelvin Functions (cont. ) The Bei functions increase exponentially. They are finite at x = 0. Bei 1 Bei 2 Bei 0 14

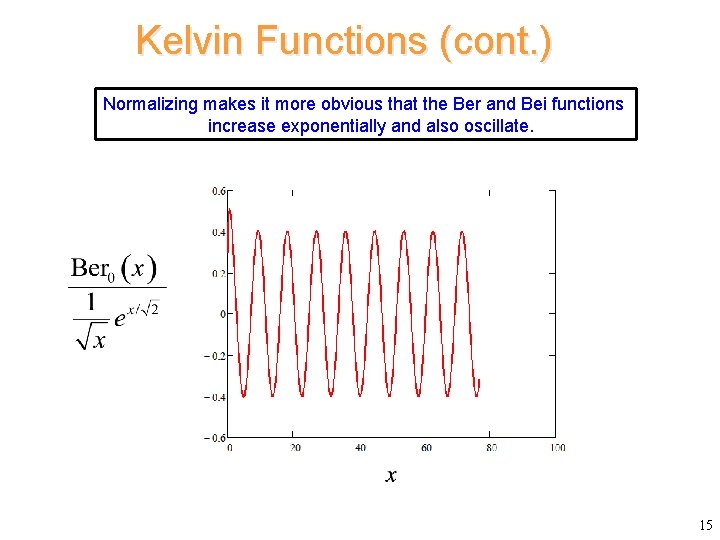
Kelvin Functions (cont. ) Normalizing makes it more obvious that the Ber and Bei functions increase exponentially and also oscillate. x 15

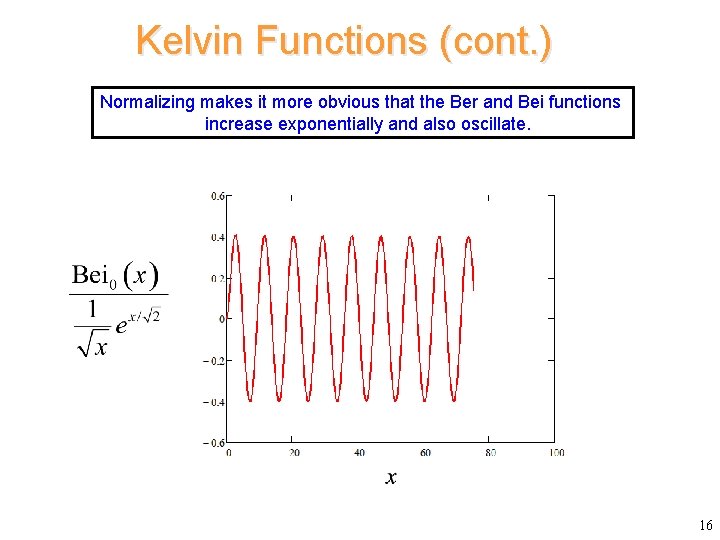
Kelvin Functions (cont. ) Normalizing makes it more obvious that the Ber and Bei functions increase exponentially and also oscillate. x 16

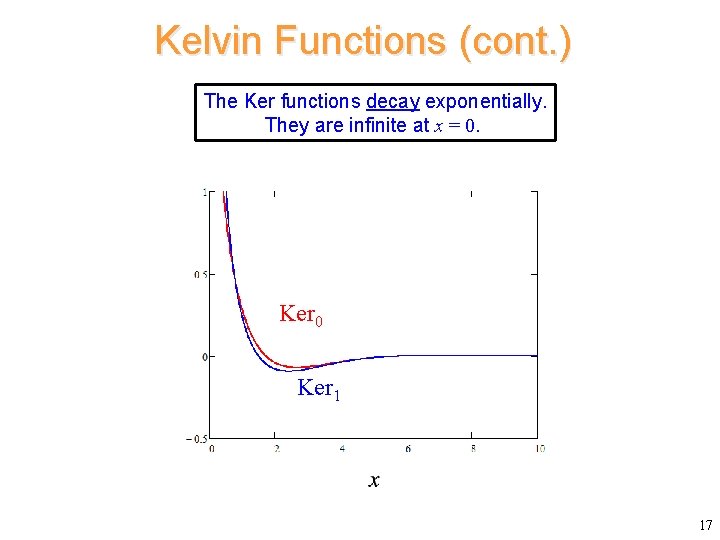
Kelvin Functions (cont. ) The Ker functions decay exponentially. They are infinite at x = 0. Ker 0 Ker 1 17

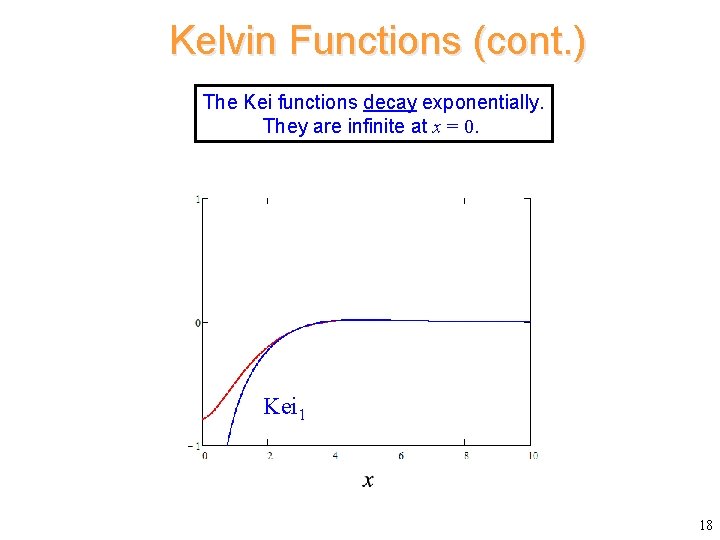
Kelvin Functions (cont. ) The Kei functions decay exponentially. They are infinite at x = 0. Kei 1 18

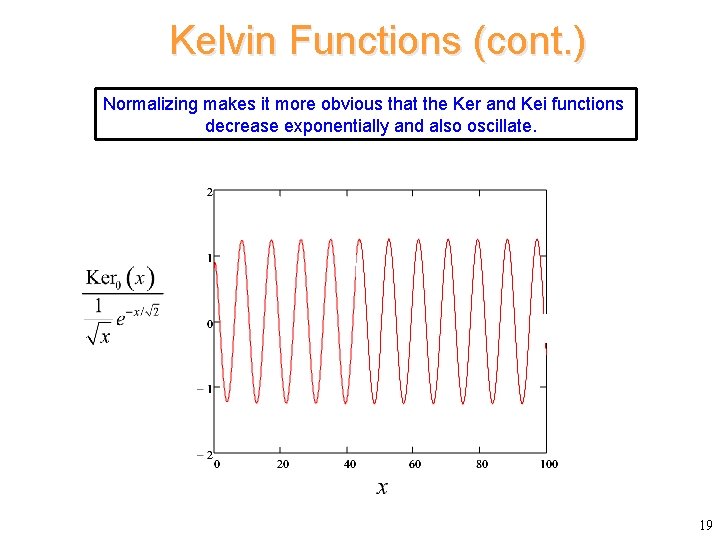
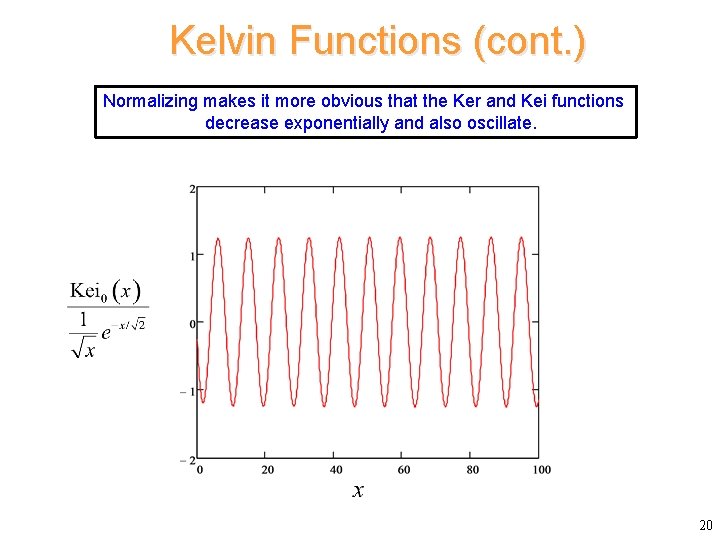
Kelvin Functions (cont. ) Normalizing makes it more obvious that the Ker and Kei functions decrease exponentially and also oscillate. 19

Kelvin Functions (cont. ) Normalizing makes it more obvious that the Ker and Kei functions decrease exponentially and also oscillate. 20