Diszkrt rendszerek Egy olyan rendszert jelent amelynl ha

Diszkrét rendszerek Egy olyan rendszert jelent amelynél ha a bemeneten egy vagy több diszkrét X(n) jel van, a rendszer kimenetén is egy vagy több Y(n) diszkrét jel lesz. Y(n) = H[x(n)] Diszkrétideju rendszer egy H matematikai operátor, amely egy jelsorozatot (bemenet) képez le egy másik jelsorozatba (kimenet)

Lineáris, diszkrét, időinvariáns rendszerek (Pl: Digitális szűrők) Egy ilyen rendszer látható a következő ábrán:

Lineáris, diszkrét, időinvariáns rendszerek n Az LDI tulajdonságai: 1. Linearitás Egy diszkrét rendszer lineáris ha a bemeneti jel ax 1(n)+bx 2(n) akkor a kimeneti jel ay 1(n)+by 2(n) Ahol a, b tetszőleges konstansok x 1(n), x 2(n) tetszőleges bemeneti jelek y 1(n), y 2(n) megfelelő válasz a bemeneti jelekre( kimeneti jelek)

Lineáris, diszkrét, időinvariáns rendszerek 2. Időinvariáns Egy diszkrét rendszer időinvariáns ha a bemeneti jel x(n-i) akkor a kimeneti jel y(n-i) bármilyen i-re Ahol i-egy tetszőleges egész szám x(n) egy tetszőleges bemeneti jel y(n) megfelelő válasz a bemeneti jelekre (kimeneti jelek) A linearitás és az időinvariáns megmagyarázható a következő ábrán (amely csak egy szorozandó tartalmaz)

Lineáris, diszkrét, időinvariáns rendszerek n n n Az első ábra következőképpen magyarázható: Tekintsük hogy x(n)= (n) akkor a y(n)=cos(n /2) (n)=cos(0) (n)= (n) Időeltolást követően a következőt kapjuk ha x(n)= (n-1) akkor a y(n)=cos(n /2) (n -1)=cos( /2) (n-1)=0 és nem a korábban kapott kimeneti jel eltolása.

Lineáris, diszkrét, időinvariáns rendszerek A második ábra nem lineáris rendszer mutat, mert ha kétszerezzük a bemeneti jelet akkor a kimeneti jel négyszeresét kapjuk. 2 x(n) y(n)= 2(xn) 2 n n a hármas ábrán könnyen látható hogy a rendszer lineáris és időinvariáns így tehát -linearitás ha x(n)= (n), akkor a y(n)=A (n) -időinvariáns ha x(n)= (n-1), akkor y(n)=A (n-1)

Lineáris, diszkrét, időinvariáns rendszerek Mint a folytonos rendszereknél a kauzalitás és a stabilitás is nagyon fontos a fizikailag megvalósítható diszkrét rendszereknél. n Kauzalitás: egy diszkrét rendszer kauzális, ha a kimeneti jel nem jelenik meg a bemeneti jel alkalmazása előtt. Azaz ha x(n)=0 n<n 0, akkor y(n)=0 n<n 0

Lineáris, diszkrét, időinvariáns rendszerek Stabilitás Egy diszkrét rendszer stabil ha bármilyen amplitudó korlatos bemeneti jel ampilitudó korlátos kimeneti jelet ad. Ha x(n) max A Akkor y(n) max B n

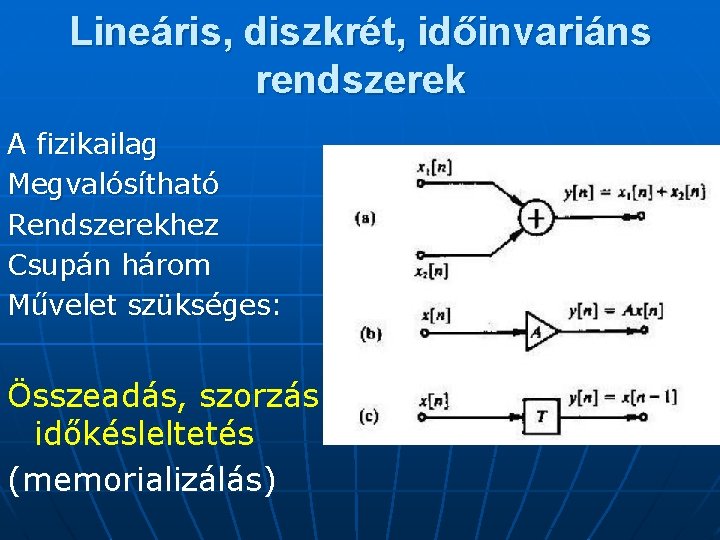
Lineáris, diszkrét, időinvariáns rendszerek A fizikailag Megvalósítható Rendszerekhez Csupán három Művelet szükséges: Összeadás, szorzás és időkésleltetés (memorializálás)

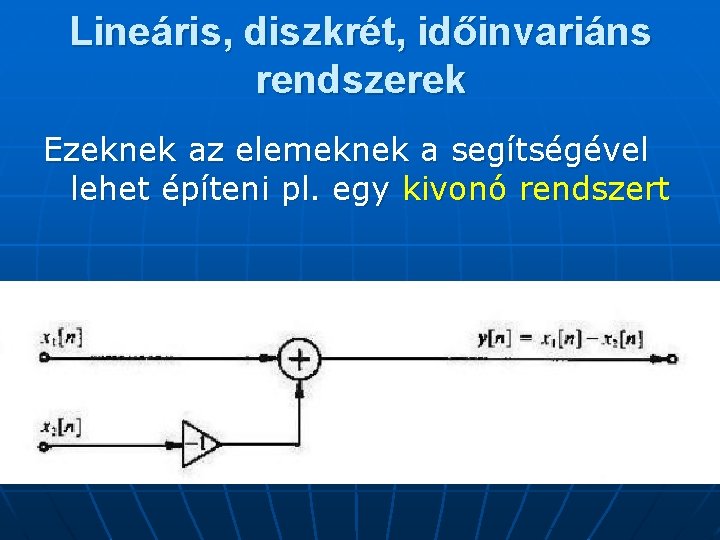
Lineáris, diszkrét, időinvariáns rendszerek Ezeknek az elemeknek a segítségével lehet építeni pl. egy kivonó rendszert

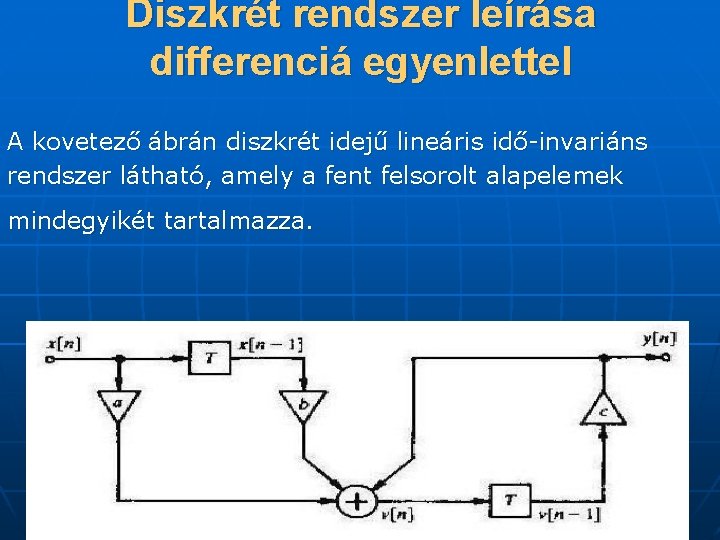
Diszkrét rendszer leírása differenciá egyenlettel A kovetező ábrán diszkrét idejű lineáris idő-invariáns rendszer látható, amely a fent felsorolt alapelemek mindegyikét tartalmazza.

Diszkrét rendszer leírása differenciá egyenlettel A fenti rendszer bemeneti és kimeneti jele közötti kapcsolatot az alábbi egyenletekkel írja le: v(n)= ax(n)+bx(n-1)+y(n) és y(n)=cv(n-1) Azok a függvények amelyek egy adott időben (v(n) y(n)) a jel értéke irható függően a jelek korábbi értékei, itt például( x(n-1), v(n-1) neveznek differencia függvények v(n) x(n-1) y(n) v(n-1)

Diszkrét rendszer leírása differenciá egyenlettel Kombinálni tudjuk a két függvényt (v(n), y(n)) úgy hogy a végén egyetlen differencia függvényt kapunk (lineáris szekvencia), amely csak a korábbi y(n-1), y(n-2)…diszkrét kimeneti értékeket valamint a x(n-1), x(n-2)… korábbi diszkrét bemeneti értékeket tartalmaz. Ha v(n)-t és y(n)-t kombináljuk Akkor y(n)=acx(n-1)+bcx(n-2)+cy(n-1) n Általában tetszőleges bemeneti x(n) jel esetén, a kezdeti feltételek ismeretében a rendszer differencia egyenletével meghatározható a kimenő y(n) jel. n

Diszkrét rendszer leírása differenciá egyenlettel Példa: ha x(n)= (n) és y(n)=0 ha n<0 Akkor y(0)=acx(-1)+bcx(-2)+cy(-1)=0 y(1)=acx(0)+bcx(-1)+cy(0)=ac y(2)=acx(1)+bcx(0)+cy(1)=(b+ac)c y(3)=acx(2)+bcx(1)+cy(2)=(b+ac)c 2. . . y(n)=acx(n-1)+bcx(n-2)+cy(n-1)= (b+ac)cn-1 és a kimeneti jel

Diszkrét rendszer leírása differenciá egyenlettel Általában egy LDI rendszer a kimeneti jel y(n) és a bemeneti jel x(n) kapcsolatot magadó funkcióval reprezentálható a következő differencia függvényt. . vagy tömörebb formában, a kimenő jelet kifejezve:

Diszkrét rendszer leírása differenciá egyenlettel Ezt az egyenlet nevezik: lineáris rendszer állandó együtthatós differencia egyenlet. Ha M=0, a rendszer nem rekurzív, vagy mozgó átlagoló. Ez esetben a rendszeregyenlet a gerjesztés-válasz kapcsolattal egyezik meg. Az ilyen rendszerek egyben véges impulzus válaszúak is (FIR rendszer). Ha M 0, a rendszer rekurzív továbbá, ha N=0, autoregresszív típusú. A differenciaegyenlet segítségével adott x(n) bemenőjel és ai, bi együtthatók esetén meghatározhatók a kimenőjel y(0), y(1), y(2), …értékei lépésről lépésre módszerrel. E módszert a gyakorlatban csak egyszerű rendszerek és egyszerű bemenő jelek esetén használják.

Diszkrét rendszer leírása differenciá egyenlettel Összetett rendszereknél hosszadalmas és körülményes, ezért diszkrét rendszereknél is általánosan használt megoldási mód a frekvenciatartományba történő transzformáció. A differenciaegyenletek diszkrét esetben is algebrai egyenletekké transzformálódnak, amelyek megoldása jóval egyszerűbb.

Diszkrét rendszer leírása differenciá egyenlettel Példa: Egy differencia egyenlet és egyik a megvalósítási lehetőség

A lineáris idő-invariáns diszkrét rendszerek súlyfüggvénye (impulzusválasza) Egy LDI egyértelműen jellemezhető a Súlyfüggvényével h(n) (Az egységnyi területű Dirac (n) adott válaszával) x(n)= (n) y(n)=h(n) Függvényre n n

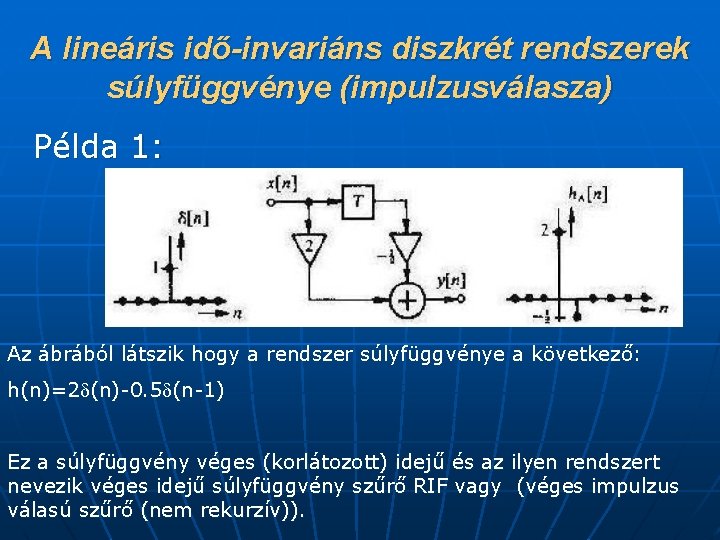
A lineáris idő-invariáns diszkrét rendszerek súlyfüggvénye (impulzusválasza) Példa 1: Az ábrából látszik hogy a rendszer súlyfüggvénye a következő: h(n)=2 (n)-0. 5 (n-1) Ez a súlyfüggvény véges (korlátozott) idejű és az ilyen rendszert nevezik véges idejű súlyfüggvény szűrő RIF vagy (véges impulzus válasú szűrő (nem rekurzív)).

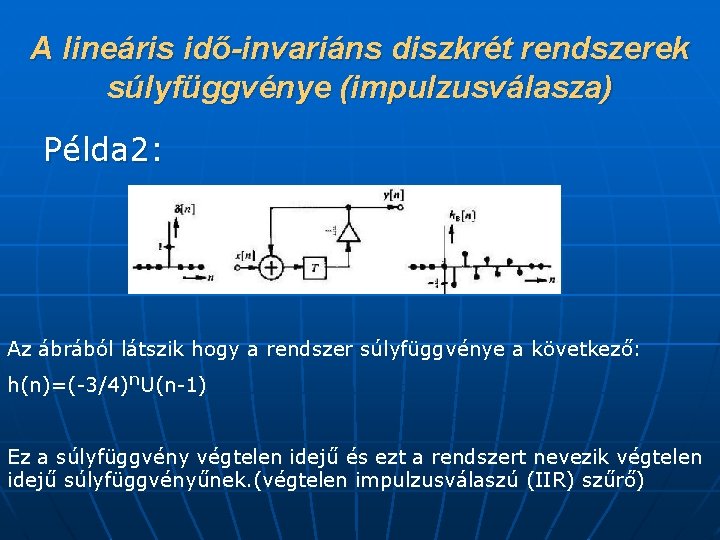
A lineáris idő-invariáns diszkrét rendszerek súlyfüggvénye (impulzusválasza) Példa 2: Az ábrából látszik hogy a rendszer súlyfüggvénye a következő: h(n)=(-3/4)n. U(n-1) Ez a súlyfüggvény végtelen idejű és ezt a rendszert nevezik végtelen idejű súlyfüggvényűnek. (végtelen impulzusválaszú (IIR) szűrő)

A lineáris idő-invariáns diszkrét rendszerek súlyfüggvénye (impulzusválasza) Eddig a mit mondtunk azt követezik hogy a súlyfüggvény h(n) ismeretében lehet számolni a kimeneti jel y(n)-nel ha a bemeneti jel x(n). A következők írhatók le: n a definícióból, ha a bemeneti jel (n) akkor a kimeneti jel h(n) n az időinvariáns tételből következik ha a bemeneti jel (n-i) akkor a kimeneti jel h(n-i) n a linearitás tételből ha a bemeneti jel x(i) (n-i) akkor a kimeneti jel x(i)h(n-i)

A lineáris idő-invariáns diszkrét rendszerek súlyfüggvénye (impulzusválasza) n Ezután kapcsoljunk a bemenetre egy tetszőleges impulzussorozatot: A válaszjel ekkor az alábbi lesz:

A lineáris idő-invariáns diszkrét rendszerek súlyfüggvénye (impulzusválasza) Röviden: Az LDI rendszer amely súlyfüggvénye h(n) adja, ha a bemeneti jel x(n), akkor a kimeneti jelet y(n) a övetező: n

Innen látható hogy a rendszer stabil vagy kauzális: n n ha a rendszer stabil akkor h(i) ha a rendszer kauzális akkor h(n)=0 ha n 0

Diszkret convolució Ha egy diszkrét rendszert időtartományban a súlyfüggvénye (h(n)-a diszkrét Dirac jelre adott válasz) jellemzi, és ha a bemenő jelet x(n)-vel jelöljük, akkor a rendszer válaszát felírhatjuk, mint a bemenő jel és a súlyfüggvény konvolutív szorzatát: Y (n ) = x (n )* h (n ) A konvolúció segítségével tetszőleges bemenőjelre meg tudjuk határozni a rendszer kimenőjelét, ha a rendszer impulzusválasza ismert, vagy általánosan, ha a fenti három jel közül bármelyik kettő ismert, akkor meghatározható a harmadik.

A konvolúció műveletét a következőképpen definiáljuk: Az egyenlet jobboldalát konvolúciós összegnek nevezzük.

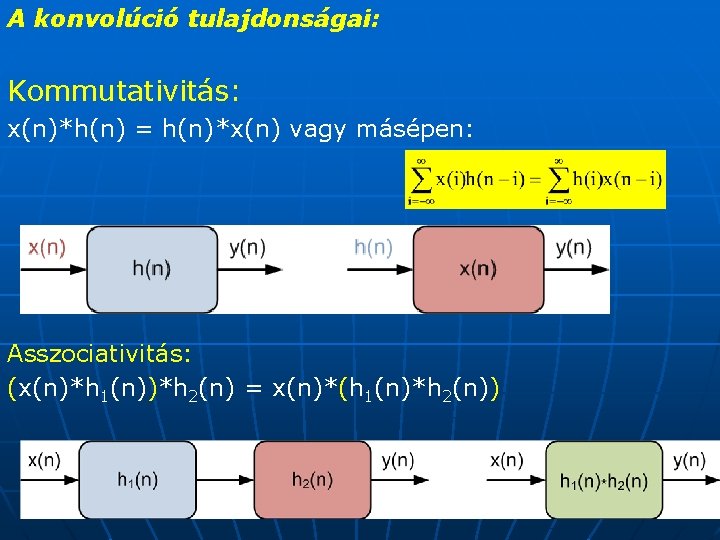
A konvolúció tulajdonságai: Kommutativitás: x(n)*h(n) = h(n)*x(n) vagy másépen: Asszociativitás: (x(n)*h 1(n))*h 2(n) = x(n)*(h 1(n)*h 2(n))

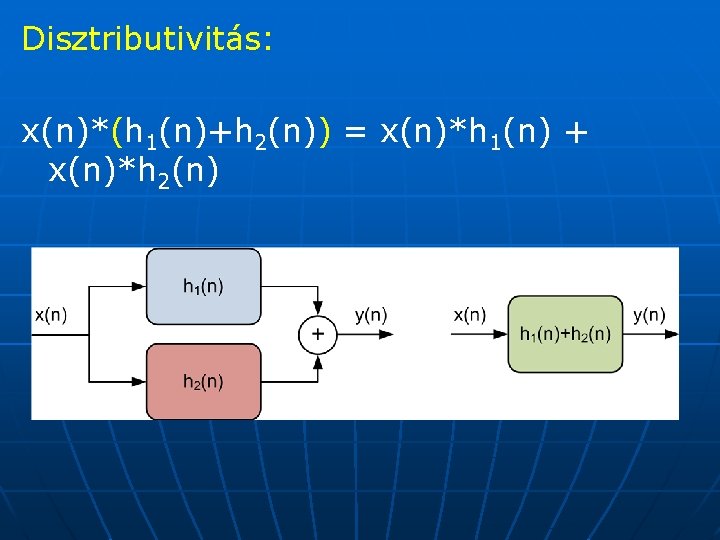
Disztributivitás: x(n)*(h 1(n)+h 2(n)) = x(n)*h 1(n) + x(n)*h 2(n)

A konvolució a követező grafikus megközelítés szemleleti: 1. x(i) és h(i) sorozatok felrajzolása i függvényében 2. h(i) sorozat tükrözése az ordináta tengelyre (h(-i) 3. h(-i) eltolása n-nel (n > 0 jobbra, n < 0 balra) (pl. : itt n=2) 4. összeadás i-vel y(2)=x(i)h(2 -i) 5. x(i) és h(n-i) sorozatok megfelelő elemeinek szorzatösszege adja y(n)-t Végestül: általában N 1és N 2 hosszúságú sorozatok konvolválásával kapott sorozat hozza N = N 1 + N 2 - 1

LDI rendszerek leírása az átviteli karakterisztika segítségével A LDI rendszerek jobban leírhatók a frekvencia tartományban (átviteli karakterisztika) mint az időtartományban ( súlyfüggvény). Tekintsünk egy rendszert melynek súlyfüggvénye h(n) és a kimeneti jele y(n) ha a bemeneti jel x(n)=cos(nw) (akkor itt a hn nem a rendszer sülyfüggvénye) x(n)=cos(nw)=ejnw/2+e-jwn/2

LDI rendszerek leírása az átviteli karakterisztika segítségével ha x 1(n)= ejnw és x 2(n)= e-jwn Akkor n és tudjuk hogy ami nem Más mint a diszkrét jelek Fourier transzformáltja

akkor y 1(n)= ejwn. H(ejw) nem más mint átviteli karakterisztikája az LDI rendszernek amely súlyfüggvénye h(n). A következők írhatók le: n y 1(n)= ejwn. H(ejw)=ejwn. Ae j =Ae j(wn+ ) ahol: A= H(ejw) komplex átviteli karakterisztika abszolút értéke és = arg H(ejw) a fázis értéke

Ugyan így meghatározhatjuk a kimenetei jel y 2(n) ha a bemeneti jel x 2(n)=e-jwn , akkor: n y 2(n)=e-jwn. H(e-jw) Használva a lineritás tételt megtudjuk határozni y(n)-t. Ha x(n)=cos(nw)=(x 1(n)+x 2(n))/2, akkor: y(n)= ejwn. H(ejw)+e-jwn. H(e-jw) /2

Ha a következő tételeket alkalmazzuk: A(ejw) = A(e-jw) (páros füg. ) és (ejw) = - (e-jw) (páratlan füg. ) akkor: y(n)=A e + e -j(wn+ ) /2 = Acos (wn+ ) j(wn+ ) Az eredmény azt mutatja, hogy a DLI rendszerben a bemeneti (itt egy cosinus jel) és a kimeneti frekvenciák azonosak de a kimeneti jel amplitudója és fázisa az átviteli karakterisztikától (H(ejw) függnek ezen a partikuláris frekvencián. Ez az egyik legfontosabb tétel a LDI rendszereknél.

LDI rendszerek leírása az átviteli karakterisztika segítségével n n Továbbá ha x(n) tetszőleges jel akkor létezik olyan Fourier Transzformáció amely adja inverz FT Azt jelenti, hogy x(n) nem más, mint végtelen exponenciális frekvencia összeadások.

LDI rendszerek leírása az átviteli karakterisztika segítségével n A linearitás tételből adódóan az LDI rendszer átfordítja a bemeneti x(n) jelet a kimeneti y(n) jelre, amelyben minden komplex exponenciál szorozva van a hozzátartozó H(ejw)

A konvolúció időtartománybeli tulajdonságai mellett további fontos a frekvenciatartományban érvényes alábbi tulajdonság. Ha adottak a h(n), x(n) és y(n) időfüggvények, Valamint e függvények Fourier-transzformáltjai, H(ejw), X(ejw) és Y(ejw) akkor az időtartománybeli és a frekvenciatartománybeli függvények között az alábbi összefüggés áll fenn:

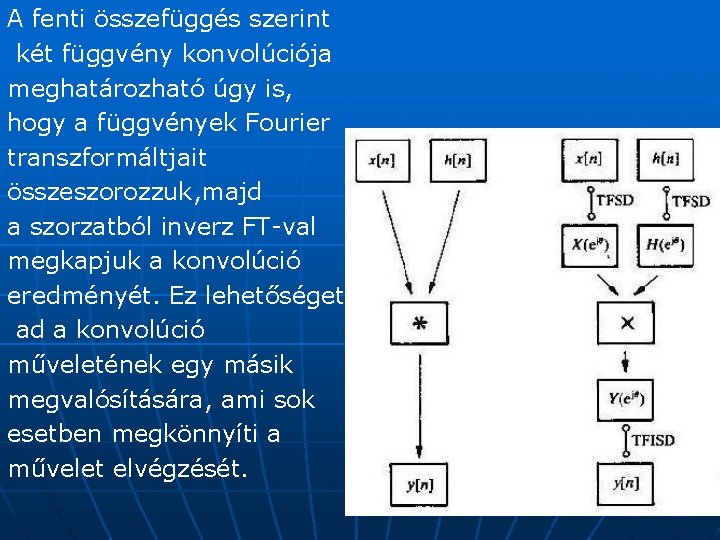
A fenti összefüggés szerint két függvény konvolúciója meghatározható úgy is, hogy a függvények Fourier transzformáltjait összeszorozzuk, majd a szorzatból inverz FT-val megkapjuk a konvolúció eredményét. Ez lehetőséget ad a konvolúció műveletének egy másik megvalósítására, ami sok esetben megkönnyíti a művelet elvégzését.

LDI rendszerek leírása az átviteli karakterisztika segítségével n 1. 2. 3. Megjegyzések: H(ejw) nem más mint a h(n) Fourier transzformáltja. Innen következik hogy H(ejw), mint minden TFSD periodikus, periódusa 2 Valós h(n) esetén (a mi átlános), a H valós része szimmetrikus páros és az Imaginárius része pedig szimmetrikus páratlan. /T

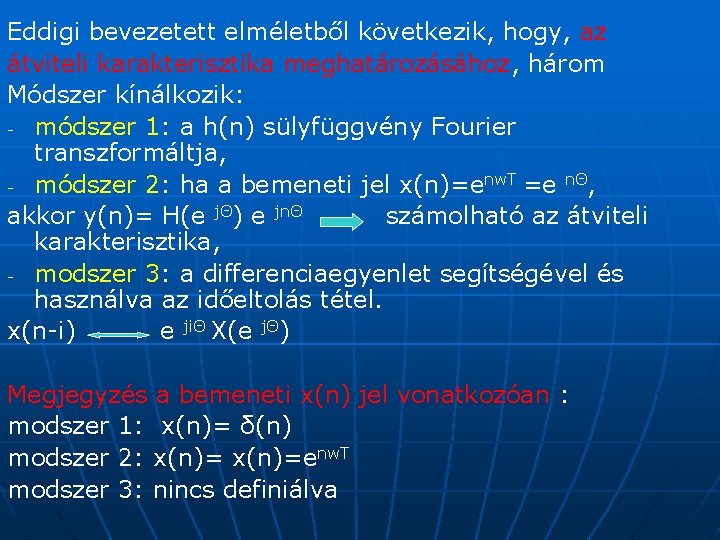
Eddigi bevezetett elméletből következik, hogy, az átviteli karakterisztika meghatározásához, három Módszer kínálkozik: - módszer 1: a h(n) sülyfüggvény Fourier transzformáltja, - módszer 2: ha a bemeneti jel x(n)=enw. T =e nΘ, akkor y(n)= H(e jΘ) e jnΘ számolható az átviteli karakterisztika, - modszer 3: a differenciaegyenlet segítségével és használva az időeltolás tétel. x(n-i) e jiΘ X(e jΘ) Megjegyzés a bemeneti x(n) jel vonatkozóan : modszer 1: x(n)= δ(n) modszer 2: x(n)=enw. T modszer 3: nincs definiálva

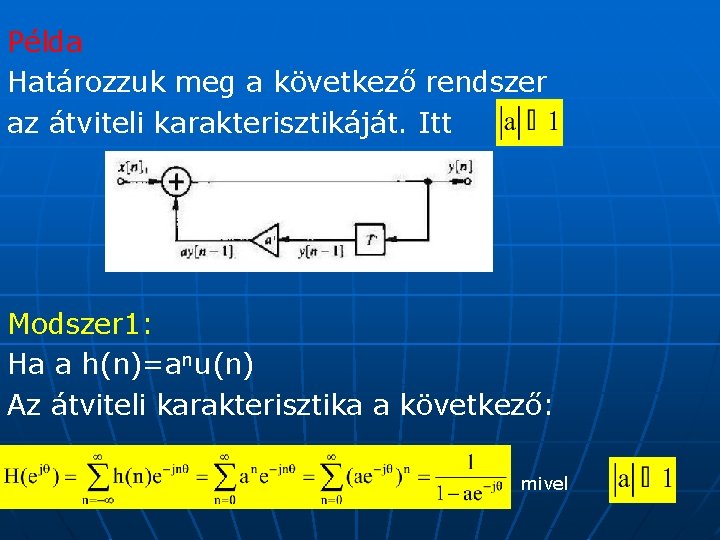
Példa Határozzuk meg a következő rendszer az átviteli karakterisztikáját. Itt Modszer 1: Ha a h(n)=anu(n) Az átviteli karakterisztika a következő: mivel

A konvolúció alkalmazásai n A konvolúciót leggyakrabban szűrők megvalósítására használják. Ha ugyanis ismerjük egy jelátviteli tag impulzusválasz függvényét, akkor a kimenőjelet a bemenőjel és az impulzusválasz konvolúciójával meghatározhatjuk. Egy adott specifikációval rendelkező szűrő megvalósításához a megfelelő impulzusválaszt kell megtalálnunk. Ezeket a szűrőket ezért konvolúciós szűrőknek is nevezik.

Fourier transzformáció A diszkrét idejű jelek leírása a frekvencia tartományban (Fourier transzformáció) A Fourier transzformáció, egy tetszőleges x[n. T] diszkrét szorozat a következő módon írható le: A folytonos jelek Fourier transzformációja szemben, két különbség figyelhető meg:

Diszkrét Fourier transzformáció Az integrál művelet helyett összegezünk mivel a jelnek csak diszkrét időpillanatokban van értéke. 2. Az w frekvenciaváltozót diszkrét esetben változóval helyettesítettük. Ez kihangsúlyozza azt, hogy X periodikus, periódusa. Emiatt elég az karakterisztika szélességű intervallumát ábrázolnunk, ahogy látható az ábrán. A tartományt alapintervallumnak nevezzük. 1.

Az függvény, mely az x[n. T] jel spektruma, komplex függvény, amely vagy a valós és képzetes komponensekkel, vagy az amplitúdóval és a fázisszöggel adható meg: Vagy egyszerűen:

Az inverz Fourier transzformáció Az inverz transzformációs egyenlet: Fourier transzformációs pár

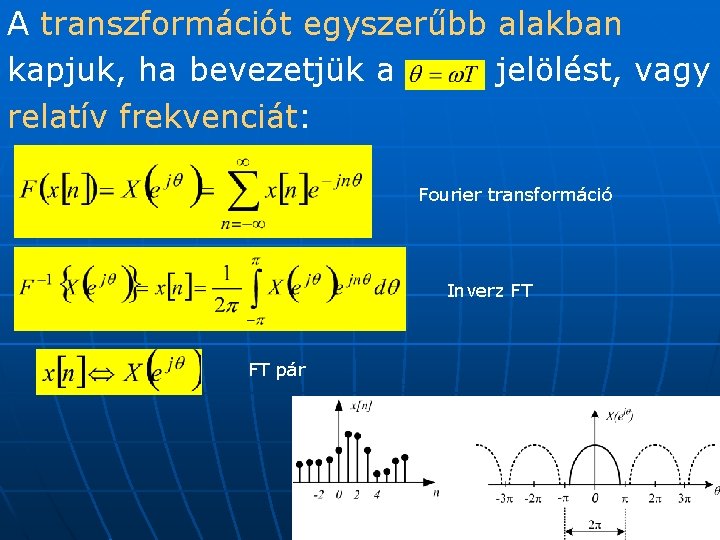
A transzformációt egyszerűbb alakban kapjuk, ha bevezetjük a jelölést, vagy relatív frekvenciát: Fourier transformáció Inverz FT FT pár

A diszkrét idejű jelek Fourier transzformációjának tulajdonságai A transzformáció tulajdonságai azonosak a folytonos jelek Fourier transzformációinál, de figyelembe kell venni, hogy csak a diszkrét időpontokra vannak értelmezve. Linearitás: ahol a és b tetszőleges konstansok. Eltolás az időtartományban:

Eltolás a frekvencia tartományban: 0 frekvenciával eltolás a spektrumban tényezővel szorzást jelent az időtartományban. Konvolúció az időtartományban: A konvolúció az időtartományban megfelel a szorzás műveletnek a frekvencia tartományban.

Konvolúció a frekvenciatartományban: A konvolúció a frekvenciatartományban megfelel a szorzás műveletnek az időtartományban. Két periodikus frekvenciafüggvény konvolúciója pedig az alábbi:

Diszkrét Fourier transzformáció periodikus jelek esetén (DFT): Legyen az xp[n] diszkrét idejű jel periodikus, melynek periódusa N. A jel ekkor eleget tesz az alábbi összefüggésnek: ahol l=0, 1, 2, …egész szám. A konvergencia problémák miatt, nem tudjuk egyben alkalmazni az előző függvények. Ezt követően, másik módszer kell találni, hogy tudjuk leírni a frekvenciatartományban az időben adott diszkrét

Diszkrét Fourier transzformáció Mivel a jel periodikus, a következőket tudjuk róla: 1. A frekvenciatartománybeli leírásban a alapharmonikus egészszámú többszörösei és esetleg a frekvenciájú komponens fordul elő. Az alapharmonikus értéke. Ez könnyen belátható egyszerű példán. Ha a jel , a jel periódus hossza N, így a jel alapharmonikus frekvenciája. 2. egyetlen periódusából minden frekvenciakomponens meghatározható. Ezek alapján a diszkrét idejű jelek Fourier transzformációs képleteinek, módosításával felírhatjuk az N pontos diszkrét Fourier transzformáció egyenletét, melynek rövidítése DFT:

Diszkrét Fourier transzformáció Az N pontos inverz diszkrét Fourier transzformáció (IDFT) képlete pedig az alábbi lesz: Ha megadjuk az xp[n] jel N darab mintavételezett érték, az xp[0], xp x[1], …, xp[N‑ 1], értékeket, vagyis az szekvencia alapintervallumát, a diszkrét Fourier transzformáció segítségével meghatározhatók az Xp[k] frekvenciaspektrum komponensei minden k egész számhoz. Xp[k] szintén periodikus, periódusa N, mivel

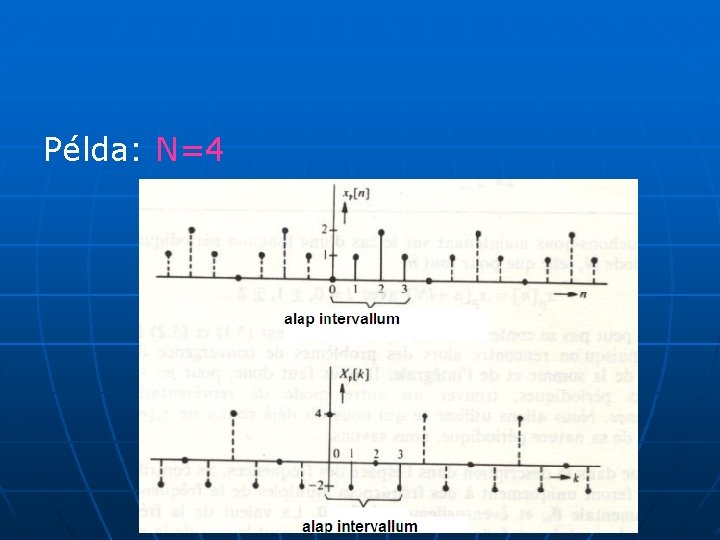
Diszkrét Fourier transzformáció A periodicitás következtében az N darab Xp[0], Xp[1], [2], …, Xp[N-1] érték, azaz az Xp[k] alapintervalluma elegendő a spektrum egyértelmű meghatározásához (lásd a példa).

Példa: N=4

Az Xp[k] diszkrét spektrum egyenlet segítségével előállítható az xp(n) mintavételezett jelsorozat. Az inverz diszkrét Fourier transzformációs egyenletben az összegezés előtti 1/N együttható megválasztásának célja, hogy a DFT és IDFT transzformációkat egymás után alkalmazva az eredmény az eredeti jel legyen. Az xp[n] és Xp[k] egyenletek a Fourier transzformációs párt alkot, melynek jelölése:

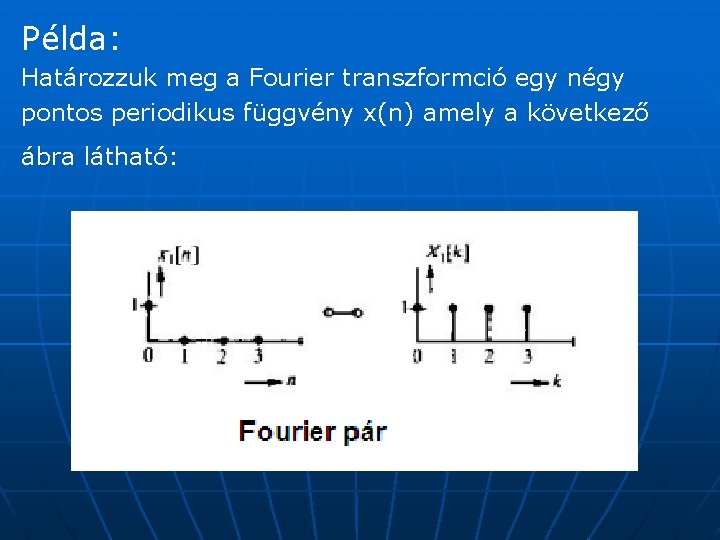
Példa: Határozzuk meg a Fourier transzformció egy négy pontos periodikus függvény x(n) amely a következő ábra látható:

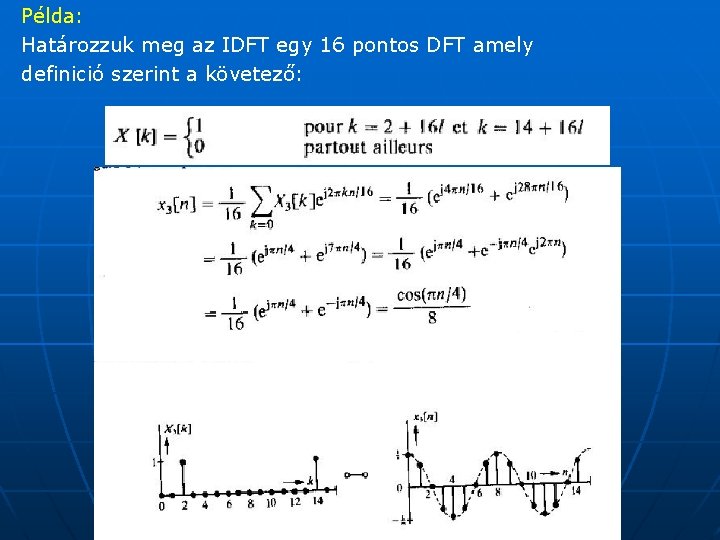
Példa: Határozzuk meg az IDFT egy 16 pontos DFT amely definició szerint a követező:

DFT a véges időtartamú diszkrét idejű jel Lásd Könyv 94. old

A DFT tulajdonságai

VOIR Transfofourierrapideanimee n

Digitális szűrők A digitális szűrők az LDI rendszerek legfontosabb elemeit képezik. Működésük differencia egyenleteikkel adható meg. Digitális szűrő definiálható mint áramkör (vagy algoritmus) amely átalakít egy bemeneti jel egy kimeneti jelre amely spektruma valamely módon meg van kötve a bemeneti jel spektruma. Alapvetően a digitális szűrők két osztályát, és pedig a rekurzív és a nemrekurzív digitális szűrők osztályát különböztetik meg.

Digitális szűrők De létezik meg egy másik módszer különböztetni a digitális szűröket: véges impulzusválaszú (FIR) és végtelen impulzusválaszú szűrőknek (IIR). A rekurzív digitális szűrök esetén a szűrő kimenetén megjelenő minden y(n) diszkrét érték a korábbi y(n-1), y(n-2), … diszkrét kimeneti értékek, valamint az x(n), x(n-1), x(n-2), … jelenlegi és korábbi diszkrét bemeneti értékek függvénye, tehát: y(n) = f {y(n-1) y(n-2), … x(n), x(n-1), x(n-2), …}

Digitális szűrők A nemrekurzív digitális szűrőket viszont az jellemzi, hogy a szúrő minden kimeneti értéke csak a jelenlegi és a megelőző bemeneti értékek függvénye, tehát: y(n) = f {x(n), x(n-1), x(n-2), …} Általában: FIR nemrekurzív digitális szűrő IIR rekurzív digitális szűrő

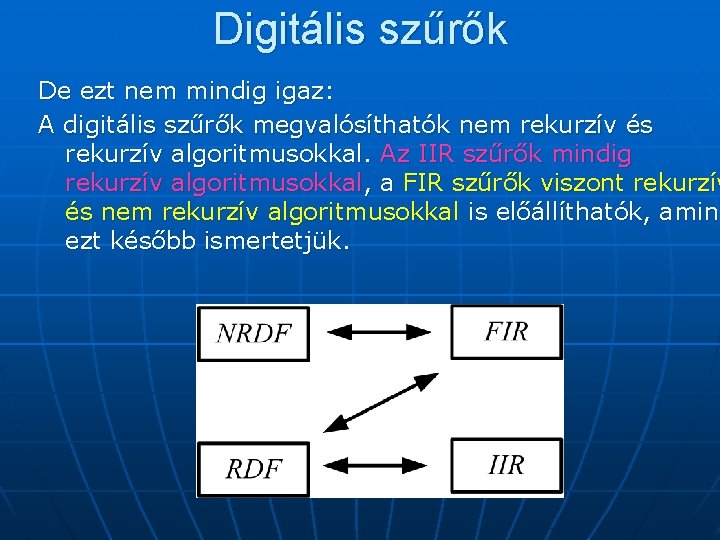
Digitális szűrők De ezt nem mindig igaz: A digitális szűrők megvalósíthatók nem rekurzív és rekurzív algoritmusokkal. Az IIR szűrők mindig rekurzív algoritmusokkal, a FIR szűrők viszont rekurzív és nem rekurzív algoritmusokkal is előállíthatók, amint ezt később ismertetjük.

Digitális szűrők A digitális szűrők realizálásahoz csupan három müveletek szükséges: időkésleltetés (memorialazálás), szorzás ill. összeadás.

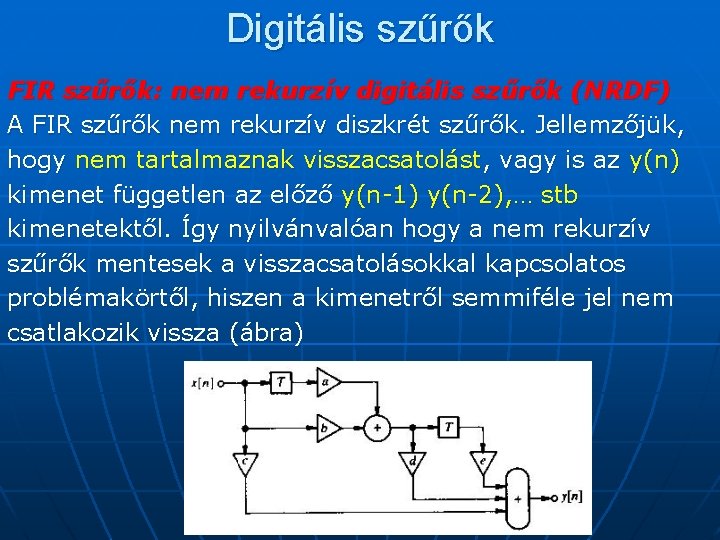
Digitális szűrők FIR szűrők: nem rekurzív digitális szűrők (NRDF) A FIR szűrők nem rekurzív diszkrét szűrők. Jellemzőjük, hogy nem tartalmaznak visszacsatolást, vagy is az y(n) kimenet független az előző y(n-1) y(n-2), … stb kimenetektől. Így nyilvánvalóan hogy a nem rekurzív szűrők mentesek a visszacsatolásokkal kapcsolatos problémakörtől, hiszen a kimenetről semmiféle jel nem csatlakozik vissza (ábra)

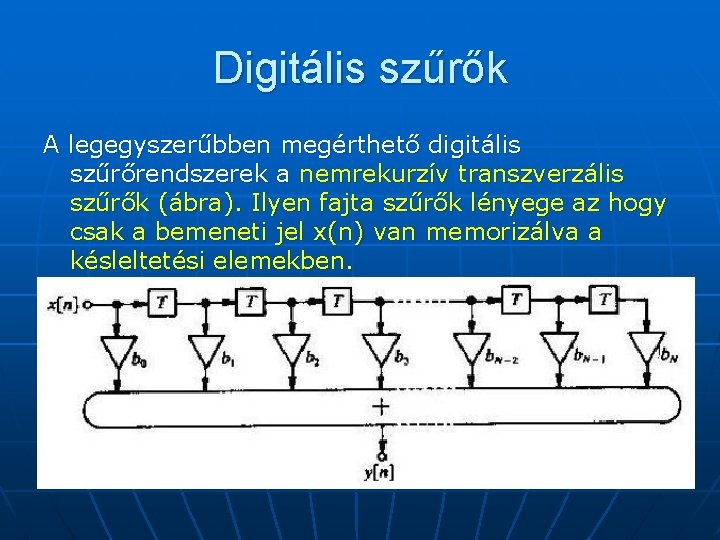
Digitális szűrők A legegyszerűbben megérthető digitális szűrőrendszerek a nemrekurzív transzverzális szűrők (ábra). Ilyen fajta szűrők lényege az hogy csak a bemeneti jel x(n) van memorizálva a késleltetési elemekben.

Digitális szűrők A nemrekurzív szűrő kauzális és a transzferfüggvénye H(z) mindig leírható a következő módon: A hozza tartózó sülyfüggvényt pedig:

Digitális szűrők A transzferfüggvényből látszik hogy a H(z) csak zérusok jönnek léttre, ill N polusok az origoban (z=0) A sülyfüggvényből látszik hogy a h(n) hosszúsága véges és maximálisan (N+1) mintából áll. A nemrekurzív szűrők mindig stabilak, amely két tényből is következik. • A diszkrét idejű rendszerek stabilitásának a feltétele, hogy az átviteli függvény összes pólusa a z sík egységsugarú tartományán belül legyen. Ez FIR szűrőknél mindig teljesül. • A stabilitás feltétele, hogy az impulzus válasz abszolút értékének összege véges legyen. FIR szűrőknél ez szintén teljesül. A FIR szűrők másik előnyös tulajdonsága a lineáris fáziskarakterisztika.

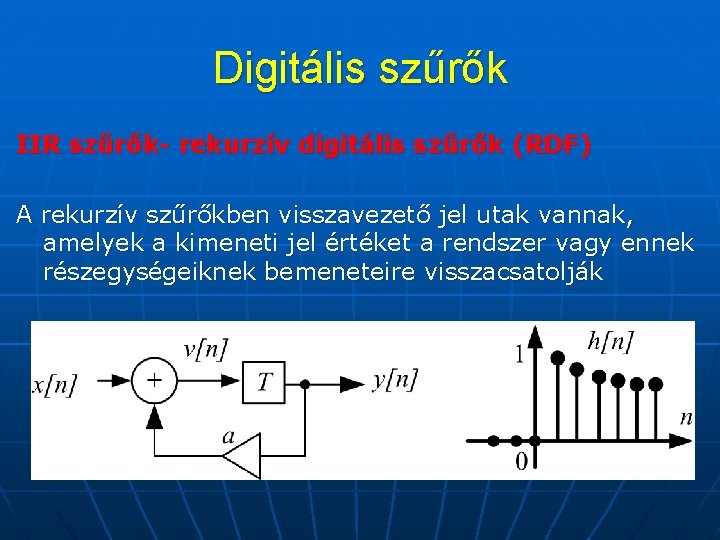
Digitális szűrők IIR szűrők- rekurzív digitális szűrők (RDF) A rekurzív szűrőkben visszavezető jel utak vannak, amelyek a kimeneti jel értéket a rendszer vagy ennek részegységeiknek bemeneteire visszacsatolják

Digitális szűrők A szűrő leírható differenciegyenlettet segítségével A sülyfüggvénye pedig: h(n)=an-1 u(n-1) Amely z-transzformácioja (transzferfüggvény) H(z)

Digitális szűrők Az IIR rekurzív szűrők különféle lehetséges struktúráihoz differencia egyenletükből kiindulva juthatunk el, az egyenlet egy-egy módosított alakjából. Direkt struktúra I. Az bemenő x(n) és az y(n) kimenő jelsorozat közötti összefüggés rekurzív szűrő esetén: n

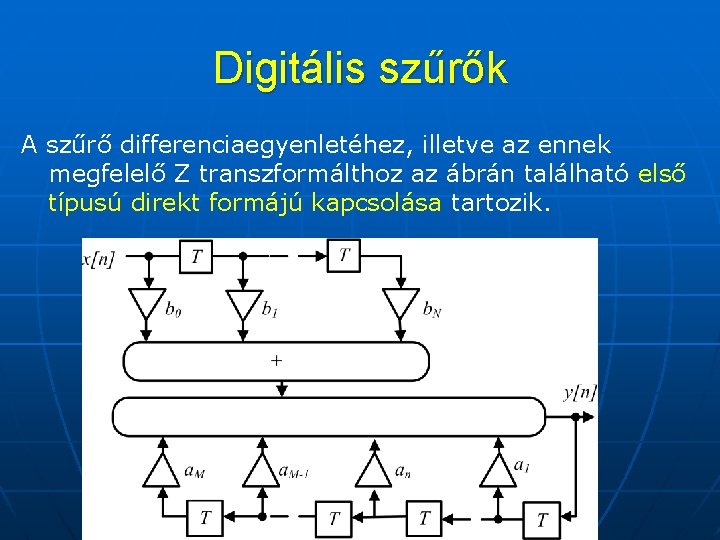
Digitális szűrők A szűrő differenciaegyenletéhez, illetve az ennek megfelelő Z transzformálthoz az ábrán található első típusú direkt formájú kapcsolása tartozik.

Digitális szűrők Láthatóan a struktúra N+M tároló elemet és N+M+1 szorzást tartalmaz. Ezenkívül mindenegyes kimeneti érték előállításához N+M+1 összeadás szükséges. A struktúrához tartozó átviteli függvény:

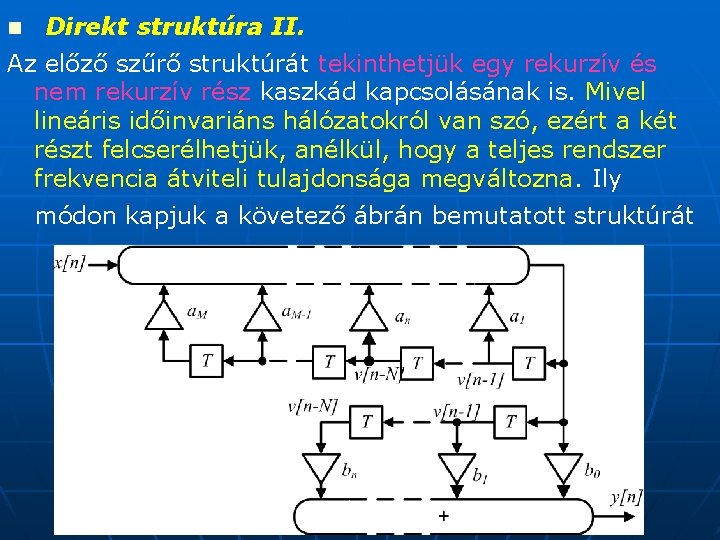
n Direkt struktúra II. Az előző szűrő struktúrát tekinthetjük egy rekurzív és nem rekurzív rész kaszkád kapcsolásának is. Mivel lineáris időinvariáns hálózatokról van szó, ezért a két részt felcserélhetjük, anélkül, hogy a teljes rendszer frekvencia átviteli tulajdonsága megváltozna. Ily módon kapjuk a követező ábrán bemutatott struktúrát

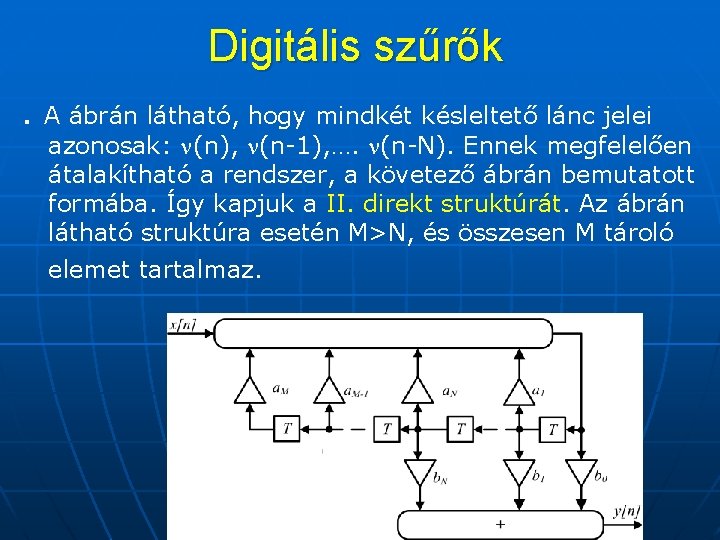
Digitális szűrők. A ábrán látható, hogy mindkét késleltető lánc jelei azonosak: (n), (n-1), …. (n-N). Ennek megfelelően átalakítható a rendszer, a követező ábrán bemutatott formába. Így kapjuk a II. direkt struktúrát. Az ábrán látható struktúra esetén M>N, és összesen M tároló elemet tartalmaz.

Az olyan struktúrákat, amelyek ugyanannyi tárolóelemet (késleltetők) tartalmaznak, mint amennyi a differenciaegyenlet fokszáma, kanonikus struktúráknak nevezzük. A direkt struktúra elnevezés magyarázata az, hogy a struktúra az átviteli függvényt közvetlen módon állítja elő. A racionális törtfüggvény minden együtthatójához illetve hatvány kifejezéséhez közvetlenül egy-egy áramköri elemet rendel hozzá. Az ai, bi együtthatók kis eltérései az átviteli függvény jelentős megváltozását okozzák. Ez azt jelenti, hogy a direkt formájú kapcsolások érzékenyek a paraméterváltozásokra. A paraméter érzékenység elkerülhető, ha a H(z) átviteli függvényt H 1(z), H 2(z), …Hk(z) első és másodfokú rész-átviteli függvények szorzatára vagy összegére osztjuk. Az egyes átviteli függvényeket külön áramkörökkel valósítjuk meg majd ezeket az átviteli függvény felbontási szabályait követve, sorosan vagy párhuzamosan összeépítjük. Az egyes áramkörök csak a saját rész-átviteli függvényük megvalósításáért ill. műszaki paramétereiért felelősek és a többi hálózati paraméterre (pólusra, zérusra)

Digitális szűrők Kaszkád struktúra A kaszkád struktúra előállításához a H(z) átviteli függvényt a következő formában írjuk fel: Az átviteli függvényt gyöktényezős alakra bontjuk, és felhasználhatjuk azt is, hogy valós impulzusválasz esetén a komplex pólusok és zérusok konjugált gyökpárokat alkotnak. Ennek megfelelően a H(z) a következő kétféle részfüggvényre (első vagy másodfokú) bontható:

Digitális szűrők Vagy Az elsőfokú alaptag egy valós zérust és egy valós pólust tartalmaz. A másodfokú tag pedig, két zérust és két pólust tartalmaz, amelyek komplexek is lehetnek.

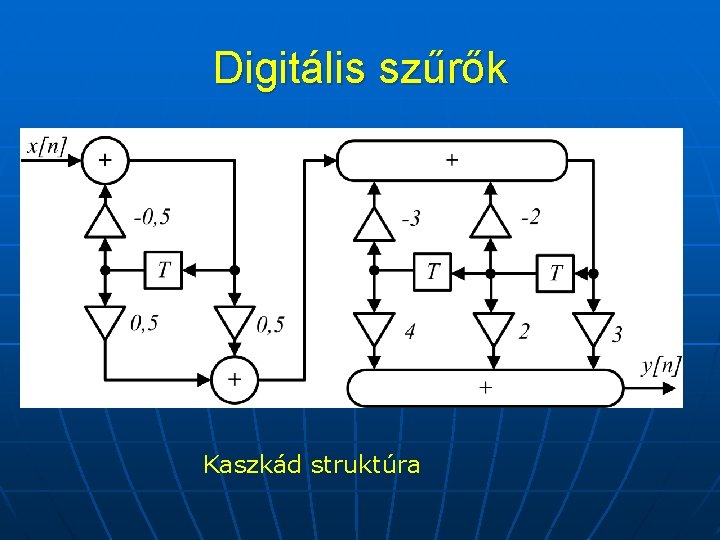
Digitális szűrők Példa: Adott egy harmadfokú rendszer amely átviteli függvénye, H(z). A kaszkád megvalósításhoz alakítsuk át első és másodfokú átviteli függvények szorzatává.

Digitális szűrők Kaszkád struktúra

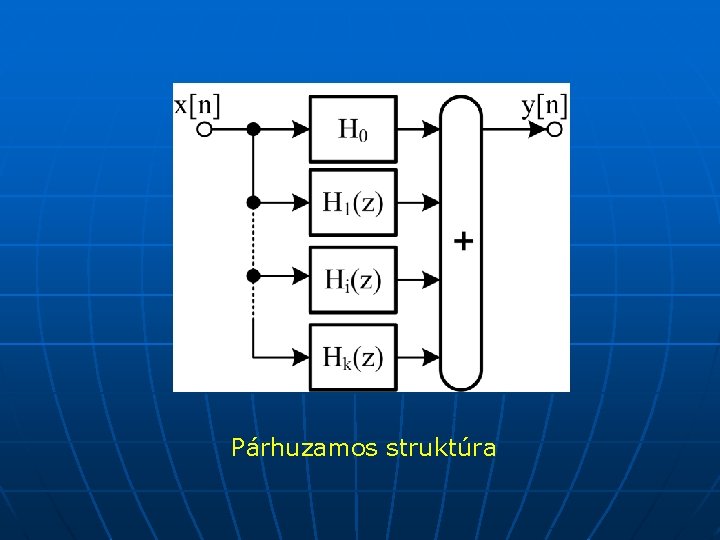
Digitális szűrők Párhuzamos struktúra Az átviteli függvényt előállíthatjuk k számú részfüggvény összegeként is: Az egyenletben H 0 konstans tag, H 1(z), H 2(z), … első vagy másodfokú alaptagok

Párhuzamos struktúra

Digitális szűrők Példaképpen egy harmadfokú szűrőt alakítsunk át párhuzamos formába A részfüggvények a következők:

Digitális szűrők Megegyezés: Léteznek sok más struktúrájú (kapcsolási forma) digitális szűrök. Példa: - Fésűszűrő - frekvencia-mintavételező struktúra

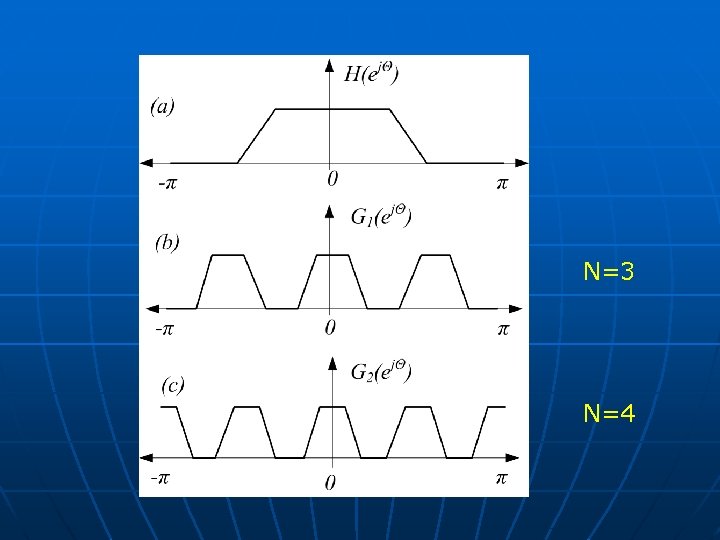
Digitális szűrők Fésűszűrő: Ha a H(z) átviteli függvényű szűrő minden tároló elemét N kaszkádba kapcsolt tárolóelemmel helyettesítünk, fésű szűrőt kapunk, melynek átviteli függvénye G(z)=H(z. N), így a frekvencia átviteli függvény a alapintervallumon N-szer ismétlődik. Példa: Ha N =3 és N =4

N=3 N=4

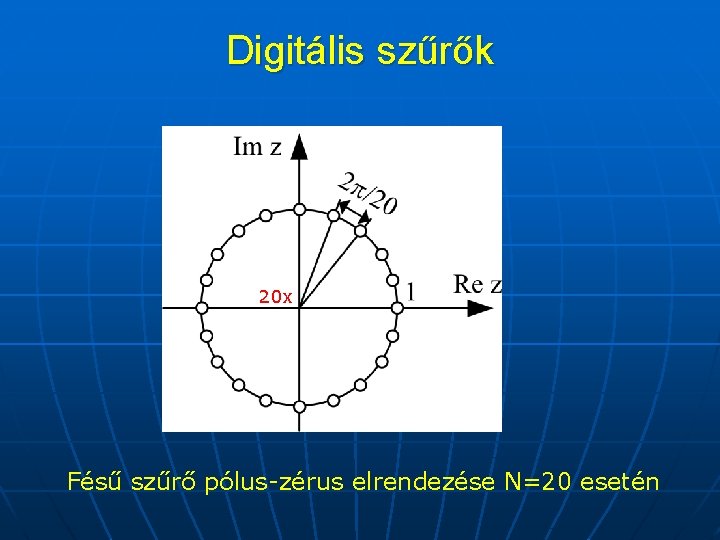
Egyszerű nem rekurzív fésű szűrőt kapunk, ha a H(z)=1 -z-1 átviteli függvényből indulunk ki. Az eredményül kapott szűrő N memória elemből , egy szorzóból és egy összeadóból áll, a szűrő átviteli függvénye: és a z tartományban az egységsugarú körön azonos távolságban elhelyezkedő N darab zérust tartalmaz.

Digitális szűrők 20 x Fésű szűrő pólus-zérus elrendezése N=20 esetén

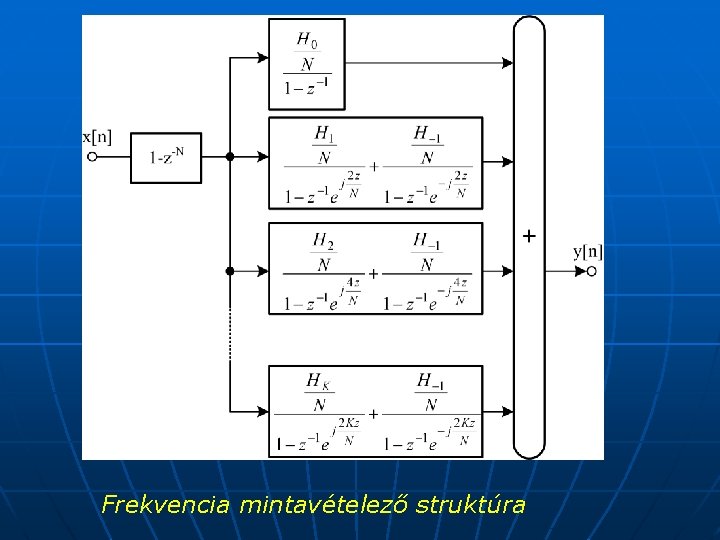
Digitális szűrők Frekvencia-mintavételező struktúra: A frekvencia-mintavételező szűrő egy fésű szűrő és az azt követő rekurzív hálózat kaszkád kapcsolásával hozható létre. A rekurzív hálózat pólusai egybeesnek a fésű szűrő zérusaival. A rekurzív rész általában párhuzamosan csatlakoztatott másodfokú részegységekből áll, de tartalmazhat elsőfokú tagot is, a z=1 vagy z=-1 pólusok megvalósításához. E struktúrával egyszerűen létrehozhatók olyan szűrők, amelyek megadott frekvenciákon pontos frekvenciaválasszal rendelkeznek.

Frekvencia mintavételező struktúra

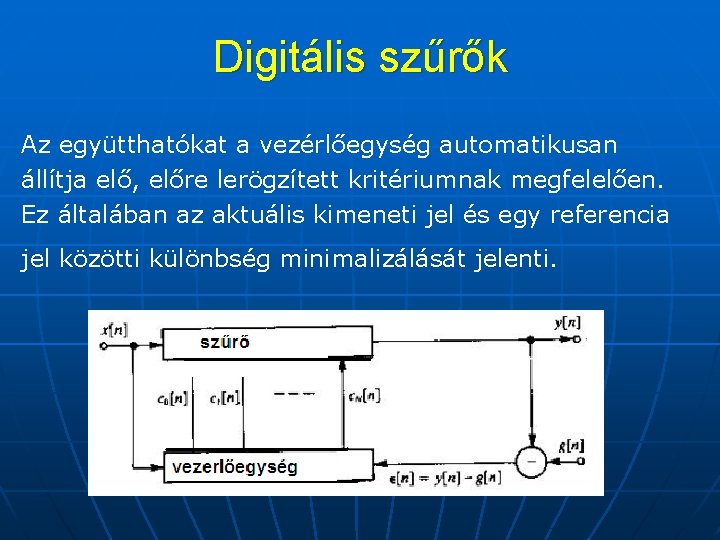
Digitális szűrők Adaptív szűrők Az adaptív szűrők olyan digitális szűrők, amelyek együtthatói nem állandók, azokat egy adaptív algoritmus automatikusan módosítja, abból a célból, hogy a szűrő frekvencia válasza meghatározott kritériumok szerint optimális legyen. Az adaptív szűrő ezért két részből áll. Az egyik rész a digitális szűrő, amelynek struktúrája elvileg az előzőkben ismertetett struktúrák bármelyike lehet, és az n-ik időpillanatban c 0[n], c 1[n], … c. N[n] együtthatókkal rendelkezik. A másik rész az adaptív algoritmust megvalósítható vezérlőegység.

Digitális szűrők Az együtthatókat a vezérlőegység automatikusan állítja elő, előre lerögzített kritériumnak megfelelően. Ez általában az aktuális kimeneti jel és egy referencia jel közötti különbség minimalizálását jelenti.

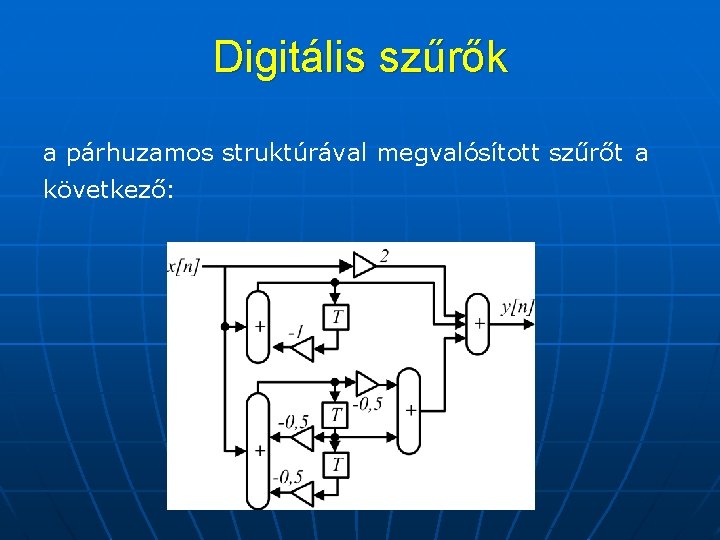
Digitális szűrők a párhuzamos struktúrával megvalósított szűrőt a következő:

Digitális szűrők méretezése és megvalósítása A digitális szűrők tervezéséhez a szűrőparaméterek specifikációja szükséges. Ezek a specifikációk a frekvenciatartománybeli karakterisztikák, mint az amplitúdó és a fázis, és egyes esetekben az időtartománybeli paraméterek, mint például a maximális jelfeldolgozási idő. Az amplitúdó-frekvencia tolerancia diagram tartalmazza a karakterisztikát, a következő ábrán látható módon. Pl. Aluláteresztő szűrő paramétereinek a specifikációja

Digitális szűrők méretezése és megvalósítása A digitális szűrők megvalósításának első lépése az átviteli karakterisztika kiválasztása. Az ideális szűrőkarakterisztikák összefoglalva a következő ábrán láthatók. A legfontosabb szűrő típusok: -Aluláteresztő szűrő -Felüláteresztő szűrő -Sáváteresztő szűrő - Sávzáró szűrő.

Az előző csoportosítás nem teljes. Létezik más fajta szűrők amelyek nem lehet sorolni az előző csoportosításához, és amelyek digitális jelfeldolgozáshoz nagy szerepet játszanak. Ezek a következők: - Differenciátor. Átviteli függvénye: - Integrátor. Átviteli függvénye: - Hilbert transzformátor. Átviteli függvénye: - Mindent áteresztő szűrő, vagy fázistoló. Átviteli függvénye:

A digitális szűrőtervezés általános lépései: - Approximáció - Szintézis és struktúra kiválasztás - Működés és szűrőparaméterek ellenőrzése -Megvalósítás. Approximáció Az approximáció folyamán a megadott szűrő specifikációhoz keressük azt a szűrő átviteli karakterisztikát, amely a specifikációknak eleget tesz. Az approximációs problémát kétféleképpen oldhatjuk meg: direkt vagy indirekt módon. Direkt módszer esetén a megoldás diszkrét idő vagy frekvencia tartományban történik. Indirekt a megoldás, ha folytonos idejű rendszert áttranszformáljuk diszkrét idejű átviteli funkcióvá.

Szintézis és struktúra kiválasztás Miután meghatároztuk az átviteli függvényt, a Szűrőt diszkrét idejű lineáris struktúrával megvalósítjuk. A struktúra kiválasztásánál szem előtt kell tartani a szükséges összeadások, szorzások, tároló elemek számát, a struktúra érzékenységét paraméter változásokra, az aritmetika pontosságára és más Egyéb.

n n Működés és szűrőparaméterek ellenőrzése Bár a szűrő együtthatókat nagy pontossággal kell meghatározni, a digitális hardver véges pontosságú. Az aritmetika lehet fix vagy lebegőpontos. Fixpontos megoldások esetén a véges pontosság a szűrő paramétereket módosítja. A tervezőnek ellenőriznie kell, hogy a megvalósított szűrő eleget tesz-e a specifikációknak. Az esetleges túlcsordulás hatását szintén vizsgálni kell. IIR szűrők esetén meg kell vizsgálni, hogy a stabilitást a hardver véges pontossága hogyan befolyásolja. Megvalósítás A digitális szűrők hardver és szoftver eszközökkel, vagy a kettő kombinációjával valósíthatók meg. A hardver lehet számítógép, mikroprocesszor vagy digitális jelprocesszor. A DSP a célra a legmegfelelőbb, mivel erre optimalizálták. Fontos szempont az eszköz kiválasztásánál a rendelkezésre álló fejlesztői környezet fejlettsége. A megvalósítás lehetséges speciális programozható integrált áramkörökkel is. Tipikusan ilyen áramkör az FPGA. Ez utóbbi megoldás a legdrágább, és a legnagyobb felkészültséget igényli a fejlesztőtől, de egyben a legnagyobb teljesítmény érhető el.

FIR szűrők tervezése - A FIR szűrők leglényegesebb tulajdonsága a véges impulzusválasz. Ha ez ismert, legalább egy formában transzverzális formában - közvetlenül megvalósítható a szűrő. Ez az oka, hogy a FIR szűrők különféle tervezési módszereiben az impulzus válasz központi szerepet játszik. Az impulzusválasz alapján eldönthető az is, hogy a FIR szűrő fázisa lineáris, vagy nem. A tervezési lépések a bevezetőben leírt szűrőtervezési lépésekkel lényegében azonosak: Szűrő specifikáció megadása Együtthatók számítása Megvalósítandó struktúra kiválasztása Szimuláció (opcionális) Megvalósítás digitális jelprocesszorral A specifikáció az előírt H(w) és (w) amplitúdó és fázis függvény megadásával történik. Általában (w)-t egyszerűen lineárisnak, vagy nem lineárisnak specifikáljuk. Az amplitúdó paramétereket a tolerancia diagrammal rögzítik.

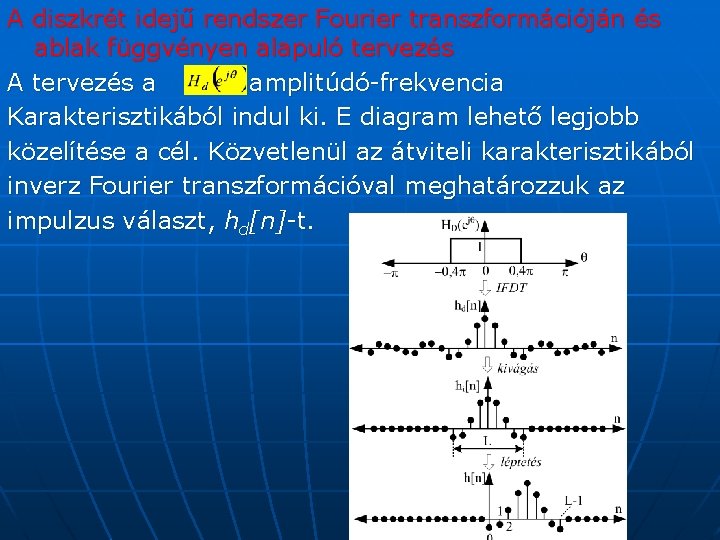
A diszkrét idejű rendszer Fourier transzformációján és ablak függvényen alapuló tervezés A tervezés a amplitúdó-frekvencia Karakterisztikából indul ki. E diagram lehető legjobb közelítése a cél. Közvetlenül az átviteli karakterisztikából inverz Fourier transzformációval meghatározzuk az impulzus választ, hd[n]-t.

Ez alapján azonban a szűrőt nem lehet megvalósítani, mivel az impulzus válasz a. ) végtelen hosszúságú, b) nem kauzális függvény, azaz hd[n] ≠ 0, n<0 esetén. Emiatt az impulzusválasz függvény hosszát elfogadható L hosszúságúra kell korlátozni, továbbá a kapott válaszfüggvényt el kell tolni (késleltetni kell), hogy az impulzus válasz kauzális legyen. A lépések az előző ábrán láthatók. A végeredmény a hd[n] függvény egy közelítése, h[n]. A h[n] impulzus válasz értékei megegyeznek a szűrő együtthatókkal. Az impulzus válasz függvény csonkítása azonban a karakterisztikában túllendülést és lengéseket okoz. Ez a Gibbs jelenség. A következő ábrán az átviteli karakterisztika látható különböző hosszúságú válaszfüggvény esetén. n

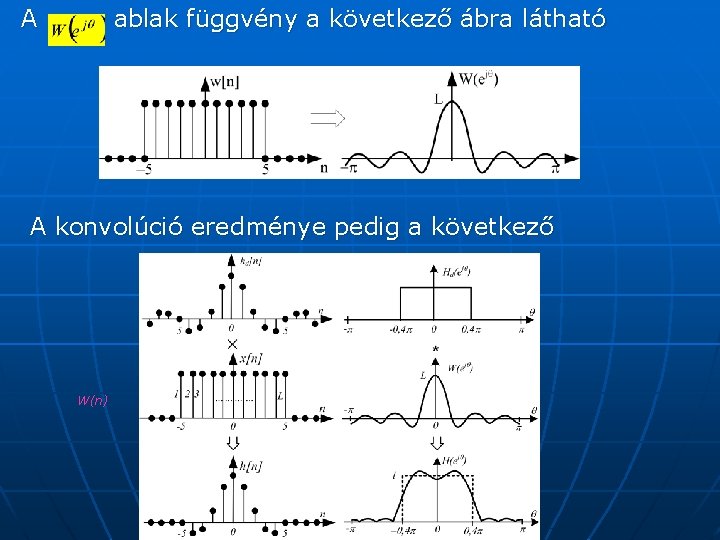
Az ideális aluláteresztő szűrő közelítése különböző hosszúságú impulzus válasz függvényekkel. A hullámosság és az átmeneti tartomány változás magyarázata a következő: A válasz függvény csonkítása az időtartományban úgy történt, hogy egy négyszögletes ablak függvénnyel, w[n]-el szoroztuk: A frekvencia tartományban ez megfelel konvolúciójának, azaz és

A ablak függvény a következő ábra látható A konvolúció eredménye pedig a következő W(n)

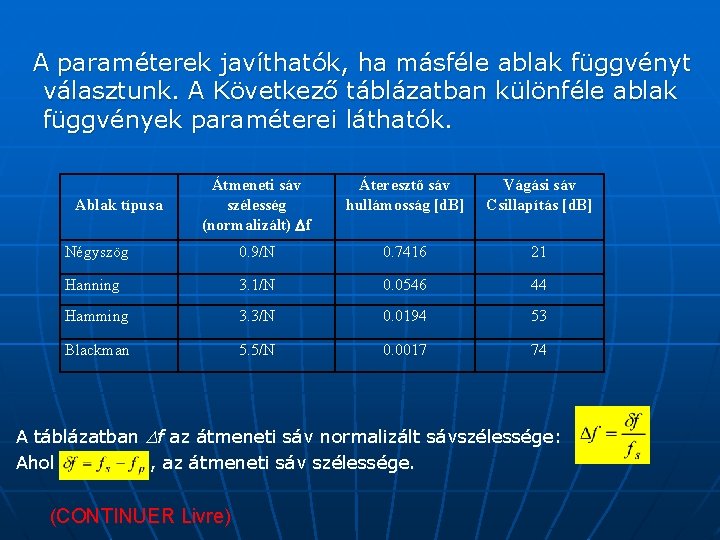
A paraméterek javíthatók, ha másféle ablak függvényt választunk. A Következő táblázatban különféle ablak függvények paraméterei láthatók. Átmeneti sáv szélesség (normalizált) f Áteresztő sáv hullámosság [d. B] Vágási sáv Csillapítás [d. B] Négyszög 0. 9/N 0. 7416 21 Hanning 3. 1/N 0. 0546 44 Hamming 3. 3/N 0. 0194 53 Blackman 5. 5/N 0. 0017 74 Ablak típusa A táblázatban f az átmeneti sáv normalizált sávszélessége: Ahol , az átmeneti sáv szélessége. (CONTINUER Livre)