Disciplined Software Engineering Lecture 9 Watts S Humphrey

Disciplined Software Engineering Lecture #9 Watts S. Humphrey Software Engineering Institute Carnegie Mellon University Pittsburgh, PA 15213 Sponsored by the U. S. Department of Defense Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 1

Design Notation - Overview The importance of notation Boolean algebra • Karnaugh maps • useful symbols • using Boolean functions Simplification Formal methods Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 2

The Importance of Notation Many software development defects are caused by misunderstandings and confusion. The notation used to represent program requirements and designs should be • precise and concise • convenient to use • commonly understood • suitable for representing a broad range of software functions Formal notations meet these criteria. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 3

Class Properties- Mathematical Notation English Symbol Example Union, sum A or B, A+B Intersection, product A and B, A*B, AB Complement, not ' All, universal 1 None, empty set 0 Copyright © 1994 Carnegie Mellon University A', not A Disciplined Software Engineering - Lecture 1 4

Using This Notation Advantages • builds familiarity with an important notation • consistent with the notation used in formal methods for proving program correctness • distinguishes logic from other expressions Disadvantages • generally takes more time to enter • will take practice to build familiarity • your coworkers may not understand it Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 5

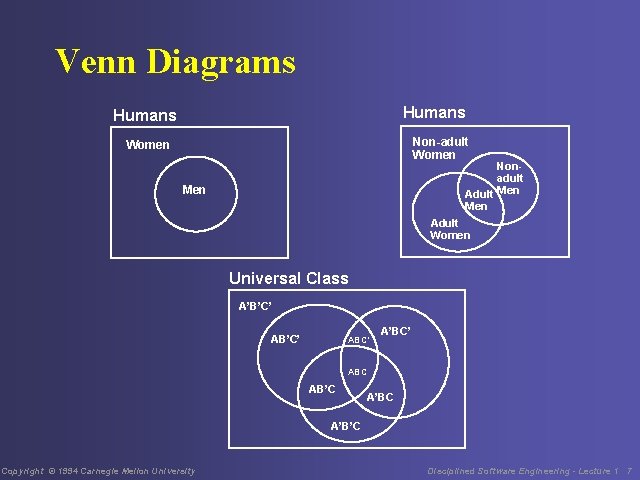
Boolean Algebra The algebra of classes • defines and manipulates class relationships • consistency - whether statements are selfconsistent • validity - whether statements represent reality Class representations • Venn diagrams • basic relationships • the universal and empty sets Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 6

Venn Diagrams Humans Non-adult Women Nonadult Adult Men Men Adult Women Universal Class A’B’C’ ABC’ A’BC’ ABC AB’C A’B’C Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 7

Properties of Classes - 1 Reflexive: for every x, x<=x Idempotent: xx=x, x+x=x Antisymmetric: if x<=y and y<=x then x=y Transitive: if x<=y and y<=z then x<=z Commutative: xy=yx, x+y=y+x Associative: x(yz)=(xy)z, x+(y+z)=(x+y)+z Distributive: x(y+z)=xy+xz, x+yz=(x+y)(x+z) Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 8

Properties of Classes - 2 Empty and universal classes: xx’=0, x+x’=1, 0<=x<=1 x 0=0, x+1=1, x+0=x, x 1=x Consistency: x<=y, xy=x, x+y=y are equivalent Absorption: x(x+y)=x+xy=x De. Morgan’s theorem: (x’)’=x, (xy)’=x’+y’, (x+y)’=x’y’ Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 9

An Example Suppose you had a switch that you wanted to be on under the following conditions • A or B or C are on • not when A and B are on • not when A and C are on You would represent this as follows On = (A+B+C)*[(A*B)+(A*C)]’ Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 10

Simplifying Boolean Expressions Consider the following guidelines when you simplify Boolean expressions • if there any primed parenthetical expressions, use De. Morgan’s theorem to remove them • look for common terms that can be factored by the distributive law • make substitutions to reduce complexity • attempt to reduce expressions to a union of intersections Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 11

Simplification Example - 1 Use the light bulb example On = (A+B+C)*[(A*B)+(A*C)]’ Apply De. Morgan’s theorem On = (A+B+C)*[(A’+B’)*(A’+C’)] Now, A’ is common to the last terms so On = (A+B+C)*[A’+(B’*C’)] Now, substitute x for B+C, and x’ for B’*C’ On = (A+x)*(A’+x’) Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 12

Simplification Example - 2 While this expression is fully simplified, it should be converted to a union of intersections • On = (A+x)*(A’+x’) • On = [(A+x)*A’]+[(A+x)*x’] • On = [(A*A’)+(x*A’)]+[(A*x’)+(x*x’)] • On = (x*A’)+(A*x’) Now, replacing x with B+C • On = [(B+C)*A’]+[A*(B’*C’)] • On = (A*B’*C’)+[A’*(B+C)] Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 13

Simplification Exercises Simplify the following expressions 1. F = X+(X’*Y) 2. F = (X+Y)+[(X*Z)+Y] 3. F = (X’*Y’*Z’)+(X*Y’*Z’) 4. F = [X’*(Y+Z’)]’*(X+Y’+Z)*(X’*Y’*Z’)’ Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 14

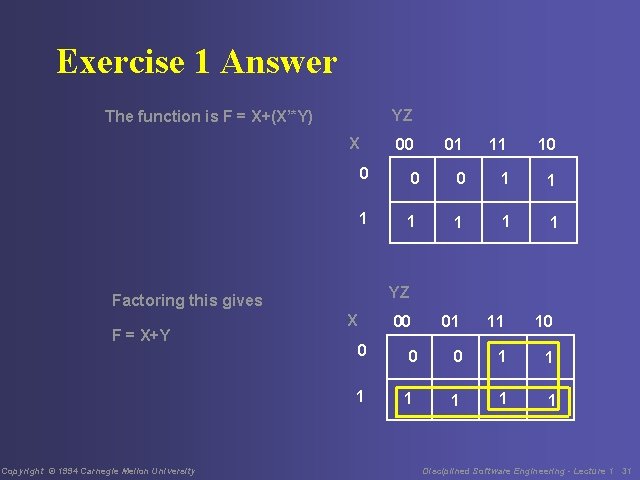
Exercise 1 Answer Starting with F = X+(X’*Y) Use the distributive law F = (X+X’)*(X+Y) Now, with the property of the universal class X+X’ = 1 AND 1*(X+Y) = X+Y So the answer is F = X+Y Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 15

Exercise 2 Answer Starting with F = (X+Y)+[(X*Z)+Y], Apply the distributive law to give F = (X+Y)+(X+Y)*(Z+Y) Now, factor out the common X+Y term F = (X+Y)*[1+(Z+Y)] By the property of the universal class, 1+Z+Y=1 so the answer is F = X+Y Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 16

Exercise 3 Answer Starting with F = (X’*Y’*Z’)+(X*Y’*Z’) Factor out the common Z’ term F = Z’*(X’Y’+XY+XY’) Factoring out the common X term F = Z’*[X’Y’+X(Y+Y’)] = Z’*(X’Y’+X) Now, with the distributive law F = Z’*(X’+X)*(Y’+X) = Z’*(Y’+X) Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 17

Exercise 4 Answer Starting with F = [X’*(Y+Z’)]’*(X+Y’+Z)*(X’*Y’*Z’)’ First apply De. Morgan’s theorem, giving F = (X+Y’Z)*(X+Y’+Z)*(X+Y+Z) Factoring out the common X term gives F = X+Y’Z*(Y’+Z)*(Y+Z) Factoring out the common Z term F = X+Y’Z*(Z+Y’Y) = X+Y’Z Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 18

Karnaugh Maps - 1 For expressions of 6 variables or less, Karnaugh maps can aid the simplification process. Karnaugh maps are a structured way to represent all possible combinations of the variables in an expression. Factoring is then done by associating related terms to achieve simplification. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 19

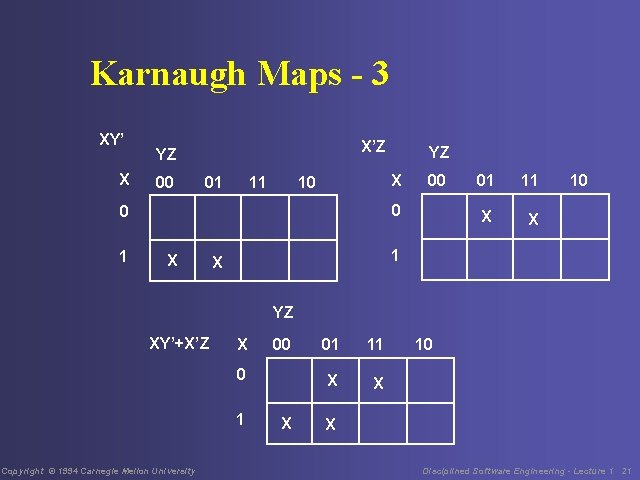
Karnaugh Maps - 2 Boolean expressions can be represented in minterm form. The minterms are the products of the variables in all possible combinations. The minterms for X and Y are: X’*Y’, X’*Y, XY There are 2**n minterms for n variables. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 20

Karnaugh Maps - 3 XY’ X X’Z YZ 00 01 11 X 10 00 0 0 1 YZ X 01 11 X X 10 1 X YZ XY’+X’Z X 00 0 1 Copyright © 1994 Carnegie Mellon University X 01 11 X X 10 X Disciplined Software Engineering - Lecture 1 21

A 4 -Variable Karnaugh Map YZ WX 00 01 11 11 10 X X X 10 Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 22

A 5 Variable Karnaugh Map XYZ VW 000 001 010 111 100 00 01 11 10 Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 23

Map Factoring - 1 When two adjacent cells both have 1 s, then those cells can be factored, eliminating the variable that is different for the two cells. For example, the 0100 and 0101 cells can be factored, eliminating the variable z. This is shown on the following map. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 24

Map Factoring - 2 YZ WX 00 01 11 11 10 X X X 10 Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 25

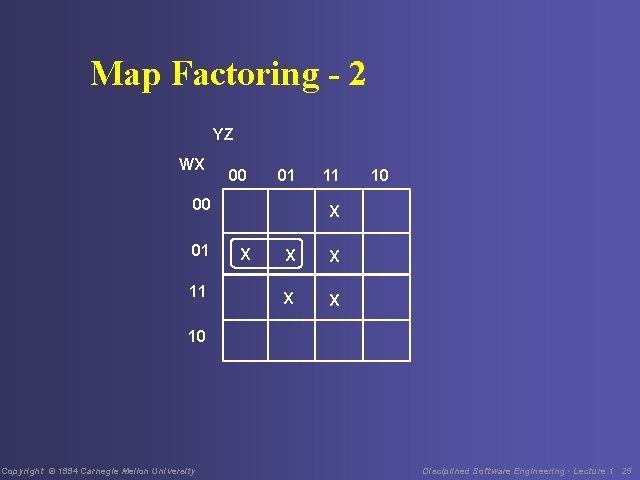
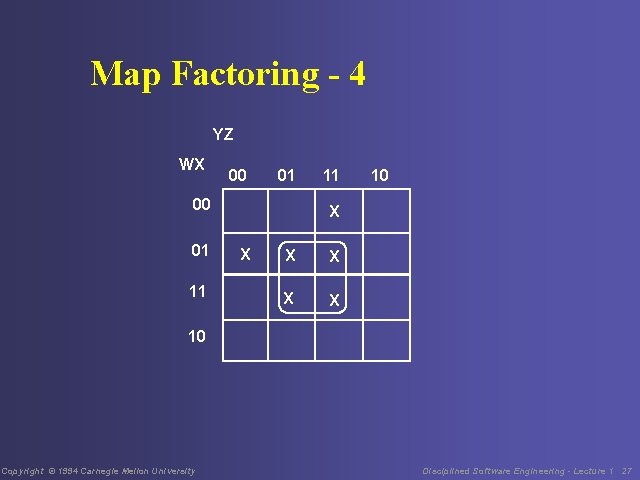
Map Factoring - 3 Similarly, when four adjacent cells have 1 s, then those cells can be factored, eliminating the two variables that are different for the four cells. For example, the 0101, 0111, 1101, and 1111 cells can be factored, eliminating the variables w and y. This is shown on the following map. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 26

Map Factoring - 4 YZ WX 00 01 11 11 10 X X X 10 Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 27

Map Factoring - 5 When all three of the possible factorings are made, the resulting expression is F = w’yz + w’xy’ + xz This is shown on the following map. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 28

Map Factoring - 6 YZ WX 00 01 11 11 10 X X X 10 W’YZ+W’XY’+XZ Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 29

Simplification Exercises Using Karnaugh Maps, simplify the following expressions 1. F = X+(X’*Y) 2. F = (X+Y)+[(X*Z)+Y] 3. F = (X’*Y’*Z’)+(X*Y’*Z’) 4. F = [X’*(Y+Z’)]’*(X+Y’+Z)*(X’*Y’*Z’)’ Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 30

Exercise 1 Answer YZ The function is F = X+(X’*Y) X 00 Copyright © 1994 Carnegie Mellon University 11 10 0 1 1 1 1 YZ Factoring this gives F = X+Y 01 X 00 01 11 10 0 1 1 1 1 Disciplined Software Engineering - Lecture 1 31

Exercise 2 Answer YZ The function is F = (X+Y)+[(X*Z)+Y] = X+Y+XZ+Y = X+Y+XZ X 00 Copyright © 1994 Carnegie Mellon University 11 10 0 1 1 1 1 YZ Factoring this gives F = X+Y 01 X 00 01 11 10 0 1 1 1 1 Disciplined Software Engineering - Lecture 1 32

Exercise 3 Answer YZ The function is F = (X’*Y’*Z’)+(X*Y’*Z’) = X’Y’Z’+XY’Z’ X 00 01 11 10 0 1 0 0 0 1 1 0 0 1 YZ Factoring this gives F = Y’Z’+XZ’ = Z’(Y’+X) Copyright © 1994 Carnegie Mellon University X 00 01 11 10 0 1 0 0 0 1 1 0 0 1 Disciplined Software Engineering - Lecture 1 33

Exercise 4 Answer - 1 X+Y’Z The function is YZ F = [X’*(Y+Z’)]’*(X+Y’+Z)*(X’*Y’*Z’)’ = (X+Y’Z)*(X+Y’+Z)*(X+Y+Z) X This can be covered in 3 maps. X+Y’+Z 00 01 11 10 0 0 1 1 1 X+Y+Z YZ YZ X 00 01 11 10 0 1 1 1 0 0 0 1 1 1 1 Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 34

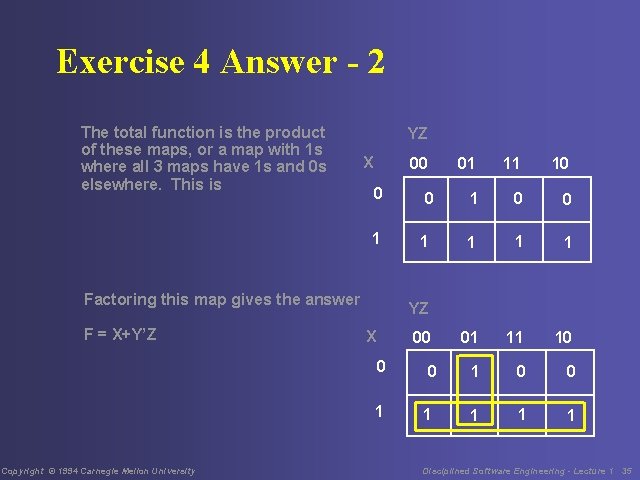
Exercise 4 Answer - 2 The total function is the product of these maps, or a map with 1 s where all 3 maps have 1 s and 0 s elsewhere. This is YZ X 00 Copyright © 1994 Carnegie Mellon University 11 10 0 0 1 1 1 01 11 10 Factoring this map gives the answer F = X+Y’Z 01 YZ X 00 0 0 1 1 1 Disciplined Software Engineering - Lecture 1 35

Factoring Zeros When factoring 1 s, the 1 s on a map are covered. This gives the minterm form of the expression. The same map can be factored by covering the 0 s and then applying De. Morgan’s Theorem. This gives the maxterm form of the expression, or the intersection of unions. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 36

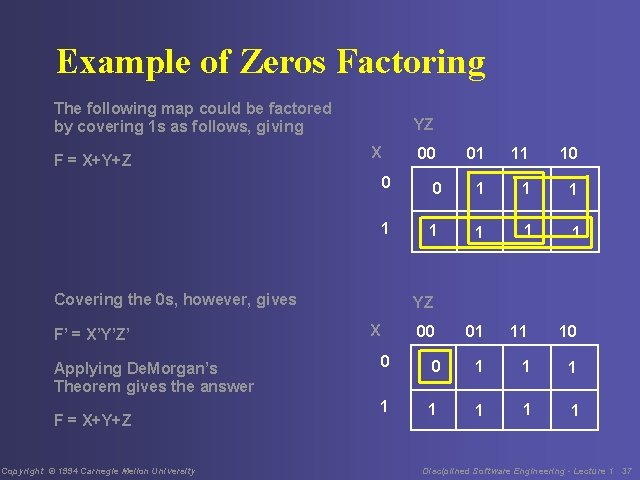
Example of Zeros Factoring The following map could be factored by covering 1 s as follows, giving F = X+Y+Z YZ X 00 Applying De. Morgan’s Theorem gives the answer F = X+Y+Z Copyright © 1994 Carnegie Mellon University 11 10 0 0 1 1 1 1 01 11 10 Covering the 0 s, however, gives F’ = X’Y’Z’ 01 YZ X 00 0 0 1 1 1 1 Disciplined Software Engineering - Lecture 1 37

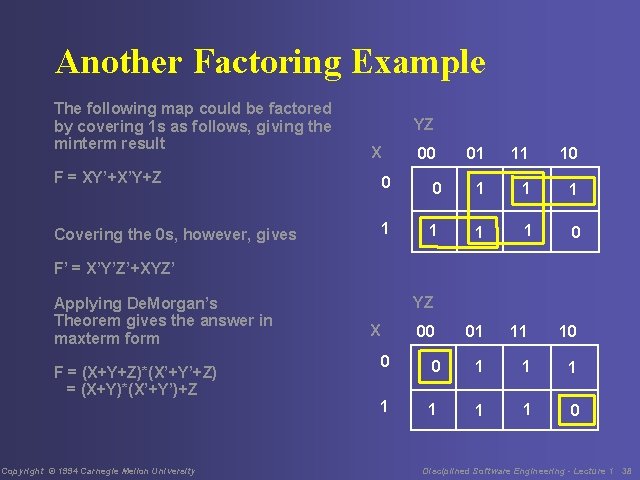
Another Factoring Example The following map could be factored by covering 1 s as follows, giving the minterm result YZ X 00 01 11 10 F = XY’+X’Y+Z 0 0 1 1 1 Covering the 0 s, however, gives 1 1 0 01 11 10 F’ = X’Y’Z’+XYZ’ Applying De. Morgan’s Theorem gives the answer in maxterm form F = (X+Y+Z)*(X’+Y’+Z) = (X+Y)*(X’+Y’)+Z Copyright © 1994 Carnegie Mellon University YZ X 00 0 0 1 1 1 1 0 Disciplined Software Engineering - Lecture 1 38

Factoring Out Zeros Sometimes, a 1 s factoring will be complicated by one or two badly placed 0 s. This can be handled as follows Factor the map as if the inconvenient 0 s were 1 s. Then, treating each of these factors as a small map, factor out the 0 s. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 39

Factoring Out 0 s Example - 1 Except for two inconvenient 0 s, this map has a very simple factoring F = Y’+W’Y = Y’+W’ Because of the 0 at W’X’Y’Z’ and the 0 at W’XYZ, however, we must factor out 0 s. Copyright © 1994 Carnegie Mellon University YZ WX 00 01 11 10 00 0 1 1 1 0 1 11 1 1 0 0 10 1 1 0 0 Disciplined Software Engineering - Lecture 1 40

Factoring Out 0 s Example - 2 The first factor, Y’, creates the mini map in the variables W, X, and Z. On this map, W’X’Z’ is factored out: YZ WX 00 01 11 10 F 1 = Y’*(W’X’Z’)’ = Y’*(W+X+Z) 00 0 1 1 1 This factoring is essentially Y’ and not W’X’Z’. 01 1 1 0 1 11 1 1 0 0 10 1 1 0 0 The second factoring is F 2 = W’Y*(XZ)’ = W’Y*(X’+Z’) So the function is F = Y’*(W+X+Z)+W’Y*(X‘+Z’) Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 41

Factoring With More Variables Karnaugh maps are possible with up to 6 variables. Beyond that, special tricks are needed. If the expression involves 6 or fewer variables in most of the terms with an occasional additional variable, an approach much like factoring out 0 s can be used. This method is called exception factoring and can be used with any number of variables. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 42

Exception Factoring - 1 To factor the following function on a 4 -variable Karnaugh map F = AX’Y’+WXY’+W’Y’Z+XY’Z+W’XY’Z’+WX’Y’ 1. Construct the function, using the variables W, X, Y, and Z. 2. For the term with the A, instead of 1, enter an A in that square. 3. In factoring out zeros, treat A as A+0. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 43

Exception Factoring - 2 First, construct the map, using only the terms containing W, X, Y, and Z. Next, enter the A term. Put an A wherever there are 0 s and nothing where there is a 1. F 1 = WXY’+W’Y’Z+XY’Z+W’XY’Z’+WX’Y’ F 2 = AX’Y’ YZ YZ WX 00 01 11 10 00 0 1 0 0 01 1 1 0 11 1 1 10 1 1 Copyright © 1994 Carnegie Mellon University WX 00 01 11 10 00 A A 0 01 0 0 0 10 A A 0 0 Disciplined Software Engineering - Lecture 1 44

Exception Factoring - 3 First, factor out the 1 s, assuming the A was a 1 F 1 = Y’ YZ WX 00 01 11 10 Next, factor out the A term, treating it as A+0 00 A 1 0 0 F = Y’*[A+(W’X’Z’)’] = Y’*(A+W+X+Z) 01 1 1 0 0 10 1 1 0 0 Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 45

Other Useful Symbols The following basic mathematical symbols are also useful in defining programming functions. - means “is a member of the set” - means “is not a member of the set” - means “for all members of the set” - means “there exists a member of the set” Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 46

Notation Examples To update a file when dataset D is a member of the file (D File) : : Update To add a number x(i), when every number i is an even integer i when (i even) : : add x(i) To clear a register when any number n is negative i when (i < 0) : : Clear Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 47

Function Completeness A set of functions is complete if it covers all possible conditions. For a complete set of functions, the Karnaugh map for the sum (or union) of the functions covers all map positions. There may be multiply-covered map positions. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 48

Function Orthogonality A set of functions is orthogonal if no two functions cover the same conditions. This means that the product (intersection) of any function with any other function is zero. i, j where (i j) => F(i)*F(j) = 0 The map may not be completely covered. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 49

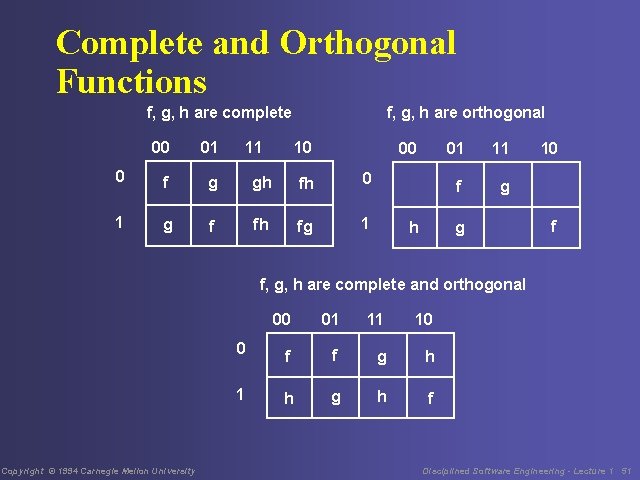
Complete and Orthogonal A set of functions is complete and orthogonal if • the functions cover all elements • no two functions cover the same elements Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 50

Complete and Orthogonal Functions f, g, h are complete 11 f, g, h are orthogonal 00 01 10 0 f g gh fh 0 1 g f fh fg 1 00 h 01 11 f g g 10 f f, g, h are complete and orthogonal Copyright © 1994 Carnegie Mellon University 00 01 11 10 0 f f g h 1 h g h f Disciplined Software Engineering - Lecture 1 51

Formal Methods - 1 Formal methods for software design have been developed based on mathematical concepts The premise of formal methods is that • computer programs can be treated as mathematical statements • the principles of mathematics thus apply • the design of a correct program can then be treated as a theorem derivation • the use of mathematically rigorous methods should thus produce correct programs. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 52

Formal Methods - 2 Formal methods typically use a program precondition, a program postcondition, and a program invariant. The program then transforms the precondition to the postcondition while preserving the invariant. To prove program correctness • prove that the program transforms the preconditions to the postconditions • and preserves the invariants Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 53

Formal Methods - 3 To formally develop a new program • start with a postcondition • derive the precondition • determine the invariants Define a program that transforms the precondition to the postcondition and preserves the invariants. If the program involves iteration, each cycle should progress toward loop termination. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 54

The Pros of Formal Notations They are precise. They can compactly represent complicated functions. They form a foundation for learning formal methods. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 55

The Cons of Formal Notations They take time to learn. They take more time to build the familiarity needed to use them for design. Your associates may not understand them. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 56

Formal Methods in This Course Adherents claim formal methods provide a rigorous way to develop quality software. Sceptics argue that they are not cost effective. While formal methods show promise, their general use will require • user training • users who make fewer errors with formal proofs than they do in software design Formal methods are not treated further in this course. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 57

Formal Method Suggestions - 1 If you are familiar with or trained in formal methods • use them with your PSP • measure your quality and productivity • compare your results to others who use such methods • compare your results to your results when you do not use formal methods • decide if these methods are effective for you Tell others what you find. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 58

Formal Method Suggestions - 2 If you are not familiar with formal methods, consider them • ask users to show you their data • take a course or study the references • try them for yourself Measure your quality and productivity before and after and decide if they are effective for you. Tell others what you find. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 59

Assignment #9 Read appendix B in the text and work through the examples Using PSP 2, write program 8 A to sort a linked list of N real numbers into ascending order. Read the program specifications in Appendix D and the PSP 2 description in Appendix C. Follow the assignment specifications in Appendix C. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 60

Messages to Remember from Lecture 9 - 1 1. A poor design notation is a source of error. 2. By using a defined and rigorous notation, you can improve the quality of your designs and eliminate defects. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 61

Messages to Remember from Lecture 9 - 2 3. Select and use an appropriate notation from among those available. 4. Try formal methods in your software development and see if they work for you. Copyright © 1994 Carnegie Mellon University Disciplined Software Engineering - Lecture 1 62