CS 203 Discrete Mathematical Structures Logic 2 Predicate

CS 203 Discrete Mathematical Structures Logic (2)

Predicate Logic - everybody loves somebody Proposition, YES or NO? 3+2=5 YES X+2=5 NO X + 2 = 5 for any choice of X in {1, 2, 3} X + 2 = 5 for some X in {1, 2, 3} YES

Predicates Ahmed eats pizza at least once a week. … Define: EP(x) = “x eats pizza at least once a week. ” Universe of Discourse - x is a student in CS 203 A predicate is a function that takes some variable(s) as arguments and returns True or False. Note that EP(x) is not a proposition, EP(Hassan) is.

Predicates A predicate is a property or description of subjects in the universe of discourse. The following predicates are all italicized : – Johnny is tall. – The bridge is structurally sound. – 17 is a prime number. Java: predicates are boolean-valued method calls– some. Linked. List. is. Empty() – is. Prime(17)

Quantifiers There are two quantifiers • Existential Quantifier “ ” reads “there exists” • Universal Quantifier “ ” reads “for all” Each is placed in front of a propositional function and binds it to obtain a proposition with semantic value.

Predicates - the universal quantifier Suppose P(x) is a predicate on some universe of discourse. Ex. B(x) = “x is carrying a backpack, ” x is set of CS 203 students. The universal quantifier of P(x) is the proposition: “P(x) is true for all x in the universe of discourse. ” We write it x P(x), and say “for all x, P(x)” x P(x) is TRUE if P(x) is true for every single x. x P(x) is FALSE if there is an x for which P(x) is x B(x)? false.

Predicates - the existential quantifier Suppose P(x) is a predicate on some universe of discourse. Ex. C(x) = “x has a cat, ” x is set of CS 203 students. The existential quantifier of P(x) is the proposition: “P(x) is true for some x in the universe of discourse. ” We write it x P(x), and say “for some x, P(x)” x P(x) is TRUE if there is an x for which P(x) is true. x C(x)? x P(x) is FALSE if P(x) is false for every single x.

Predicates - the existential quantifier Universe of discourse is people in this room. B(x) = “x is wearing sneakers. ” L(x) = “x is at least 16 years old. ” Y(x)= “x is less than 24 years old. ” Are either of these propositions true? a) b) x B(x) x (Y(x) L(x)) A: only a is true B: only b is true C: both are true D: neither is true

Predicates - more examples L(x) = “x is a lion. ” Universe of discourse is all creatures. F(x) = “x is fierce. ” C(x) = “x drinks coffee. ” All lions are fierce. Some lions don’t drink coffee. x (L(x) F(x)) x (L(x) C(x)) Some fierce creatures don’t drink coffee. x (F(x) C(x))

Predicates - more examples B(x) = “x is a hummingbird. ” L(x) = “x is a large bird. ” H(x) = “x lives on honey. ” R(x) = “x is richly colored. ” Universe of discourse is all creatures. All hummingbirds are richly colored. No large birds live on honey. x (B(x) R(x)) x (L(x) H(x)) Birds that do not live on honey are dully colored. x ( H(x) R(x))

Fundamentals of Logic The Use of Quantifiers Ex universe: real numbers x=4 x=1 x=5, 6, . . x=-1

Predicates - the universal quantifier Universe of discourse is people in this Hall. B(x) = “x is wearing sneakers. ” L(x) = “x is at least 18 years old. ” Y(x)= “x is less than 24 years old. ” Are either of these propositions true? a) b) x (Y(x) B(x)) x (Y(x) L(x)) A: only a is true B: only b is true C: both are true D: neither is true

Predicates - quantifier negation Not all large birds live on honey. x (L(x) H(x)) x P(x) means “P(x) is true for every x. ” What about x P(x) ? Not [“P(x) is true for every x. ”] “There is an x for which P(x) is not true. ” x P(x) So, x P(x) is the same as x P(x). x (L(x) H(x))

Predicates - quantifier negation No large birds live on honey. x (L(x) H(x)) x P(x) means “P(x) is true for some x. ” What about x P(x) ? Not [“P(x) is true for some x. ”] “P(x) is not true for all x. ” x P(x) So, x P(x) is the same as x P(x). x (L(x) H(x))

Predicates - quantifier negation So, x P(x) is the same as x P(x). General rule: to negate a quantifier, move negation to the right, changing quantifiers as you go.

Fundamentals of Logic Ex. p(x): x is odd. q(x): x 2 -1 is even. Negate (If x is odd, then x 2 -1 is even. ) There exists an integer x such that x is odd and x 2 -1 is odd. (a false statement, the original is true)

Predicates - quantifier negation No large birds live on honey. x (L(x) H(x)) Negation rule x ( L(x) H(x)) De. Morgan’s x (L(x) H(x)) Subst for What’s wrong with this proof?

Fundamentals of Logic multiple variables

Fundamentals of Logic BUT Ex. p(x, y): x+y=17. : For every integer x, there exists an integer y such that x+y=17. (TRUE) : There exists an integer y so that for all integer x, x+y=17. (FALSE) Therefore,

Order matters Set the universe of discourse to be all natural numbers {0, 1, 2, 3, … }. Let R (x, y ) = “x < y”. Q 1: What does x y R (x, y ) mean? Q 2: What does y x R (x, y ) mean? 20

Order matters R (x, y ) = “x < y” A 1: x y R (x, y ): “All numbers x admit a bigger number y ” A 2: y x R (x, y ): “Some number y is bigger than all x” Q: What’s the true value of each expression? 21

More Practice for Predicate Logic • Nermin likes all movies that Rehab likes (and possibly more). • x [Movie(x) Likes(Rehab, x) Likes(Nermin, x)] • There is exactly one AU professor who won a Nobel prize • x[AU_Prof(x) Wins(x, Nobel. Prize)] y, z[y z AU_Prof(y) AU_Prof(z) Wins(y, Nobel. Prize) Wins(z, Nobel. Prize)]

Review of Boolean algebra • Not is a horizontal bar above the number – 0=1 – 1=0 • Or is a plus – – 0+0 = 0 0+1 = 1 1+0 = 1 1+1 = 1 • And is multiplication – – – 23 – 0*0 = 0 0*1 = 0 1*0 = 0 1*1 = 1

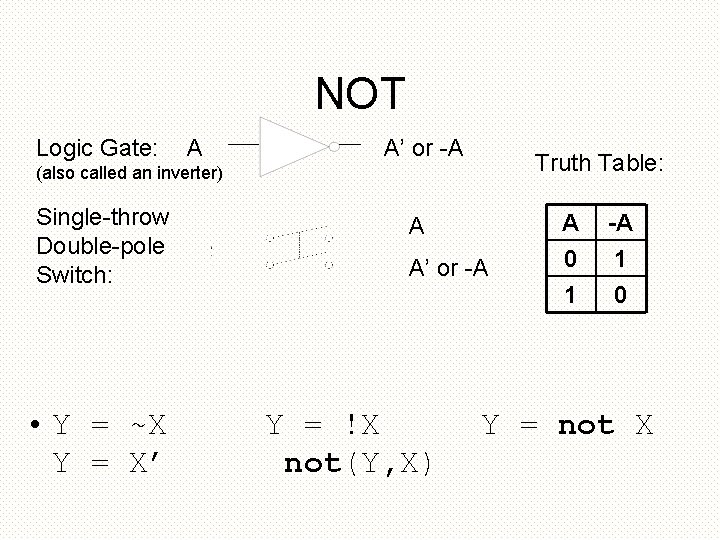
NOT Logic Gate: A A’ or -A Truth Table: (also called an inverter) Single-throw Double-pole Switch: • Y = ~X Y = X’ A A’ or -A Y = !X not(Y, X) A 0 1 -A 1 0 Y = not X

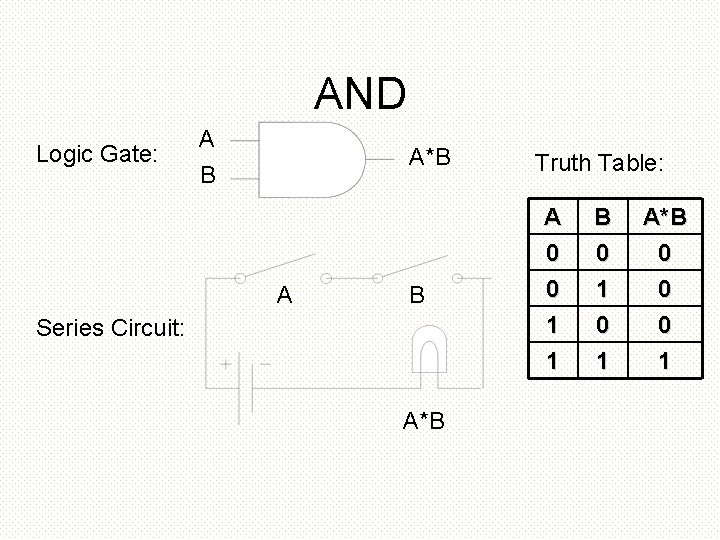
AND Logic Gate: A A*B B A B Series Circuit: A*B Truth Table: A 0 0 1 B 0 1 0 A*B 0 0 0 1 1 1

AND • X & Y (Verilog and ABEL) • X and Y (VHDL) • X Y • X * Y • XY (textbook) • and(Z, X, Y) (Verilog) V U

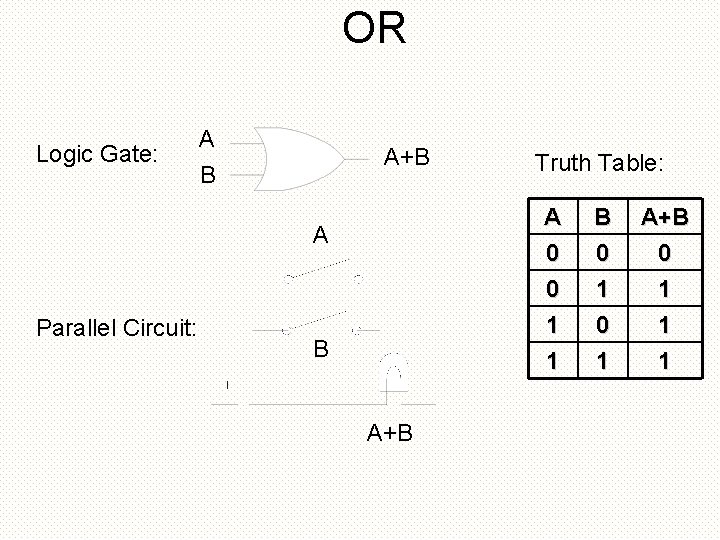
OR Logic Gate: A A+B B A Parallel Circuit: B A+B Truth Table: A 0 0 1 B 0 1 0 A+B 0 1 1 1

OR • X | Y • X # Y • X or Y • X + Y • X V Y • X U Y • or(Z, X, Y) (Verilog) (ABEL) (VHDL) (textbook) (Verilog)

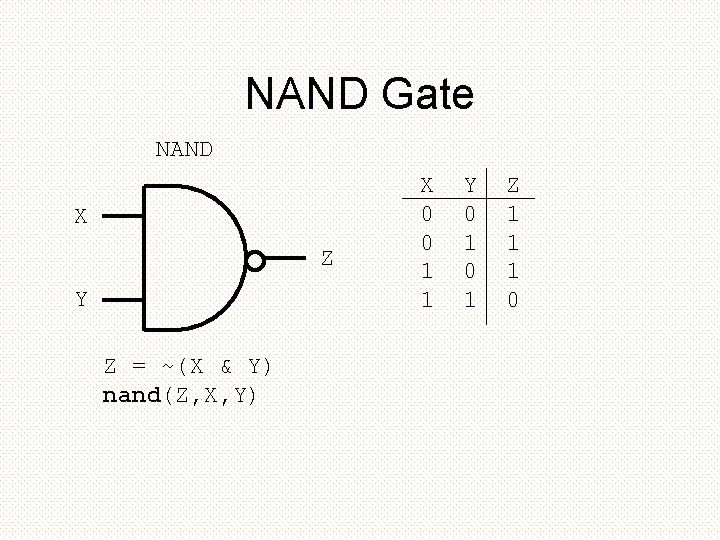
NAND Gate NAND X Z Y Z = ~(X & Y) nand(Z, X, Y) X 0 0 1 1 Y 0 1 Z 1 1 1 0

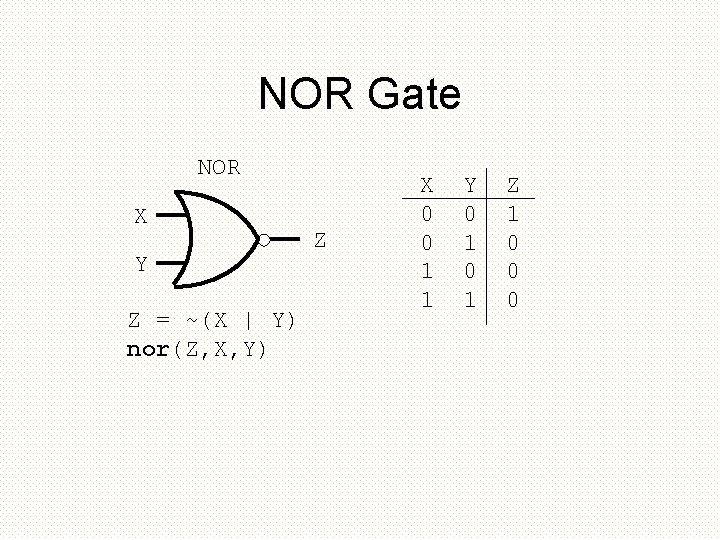
NOR Gate NOR X Y Z = ~(X | Y) nor(Z, X, Y) Z X 0 0 1 1 Y 0 1 Z 1 0 0 0

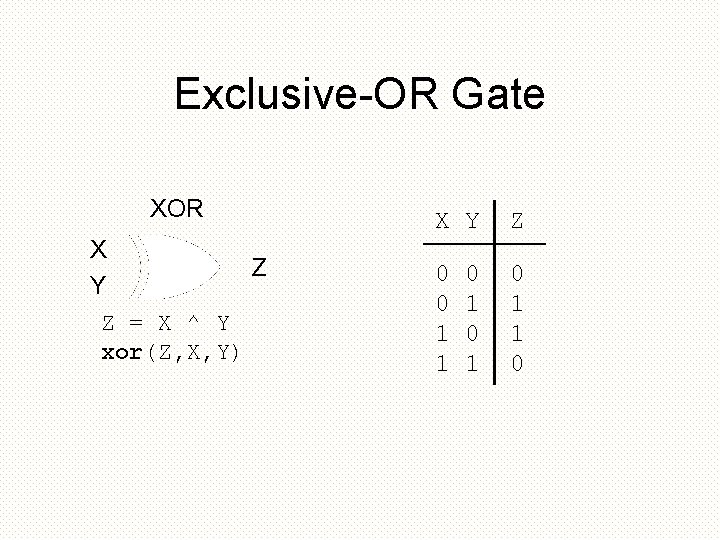
Exclusive-OR Gate XOR X Z Y Z = X ^ Y xor(Z, X, Y) X Y Z 0 0 1 1 0 0 1

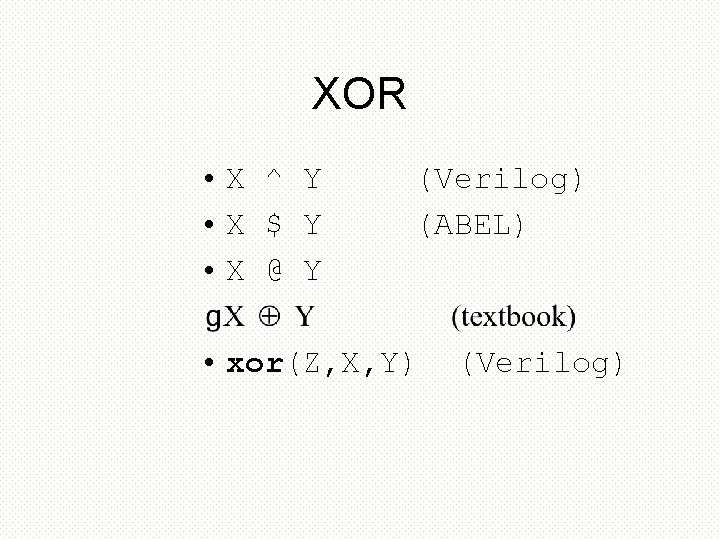
XOR • X ^ Y • X $ Y • X @ Y (Verilog) (ABEL) • xor(Z, X, Y) (Verilog)

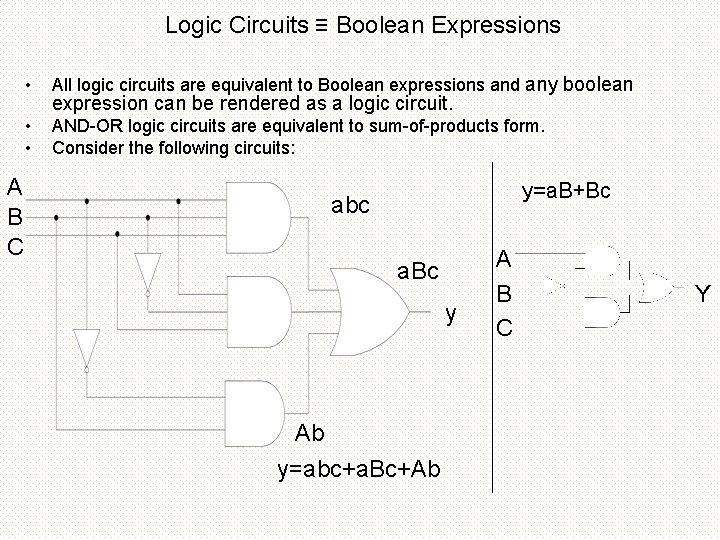
Logic Circuits ≡ Boolean Expressions A B C • All logic circuits are equivalent to Boolean expressions and any boolean • • AND-OR logic circuits are equivalent to sum-of-products form. Consider the following circuits: expression can be rendered as a logic circuit. y=a. B+Bc abc a. Bc y Ab y=abc+a. Bc+Ab A B C Y

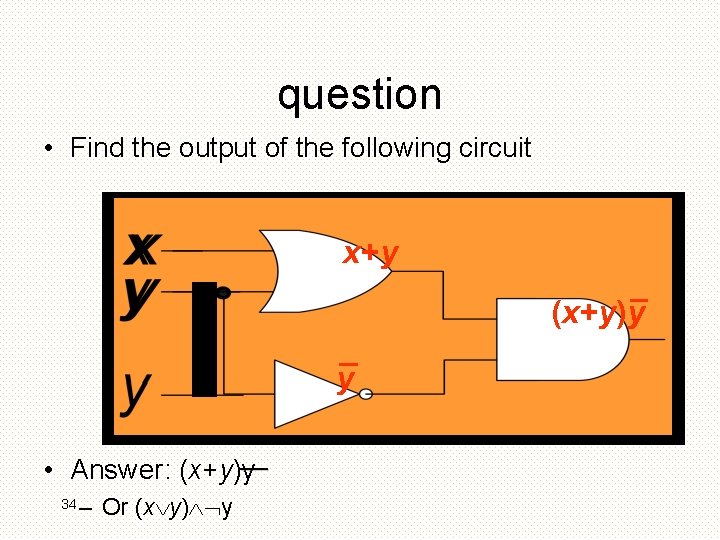
question • Find the output of the following circuit x+y (x+y)y y __ • Answer: (x+y)y__ 34 – Or (x y) y

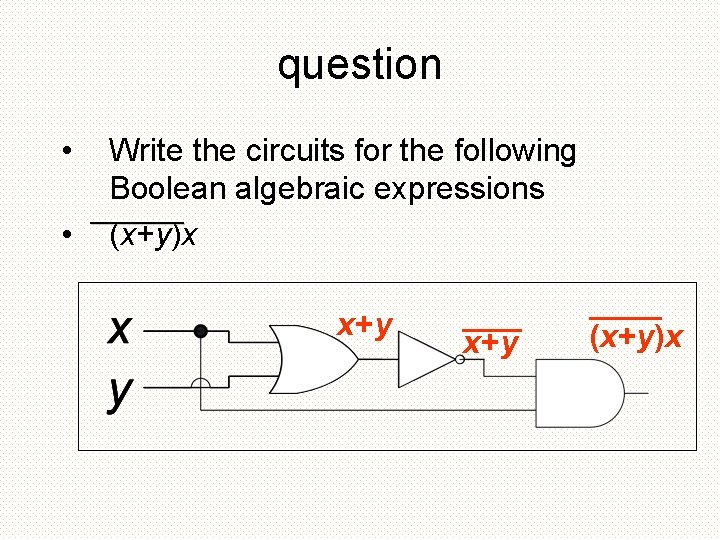
question • Write the circuits for the following Boolean algebraic expressions _______ • (x+y)x x+y (x+y)x

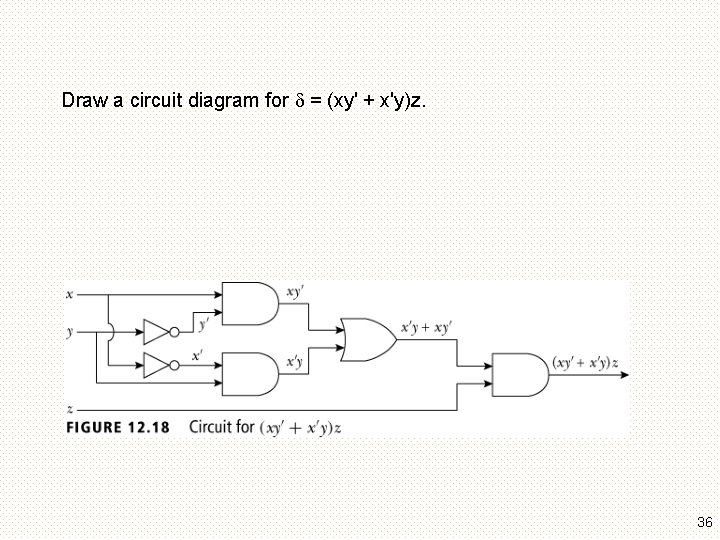
Draw a circuit diagram for = (xy' + x'y)z. 36

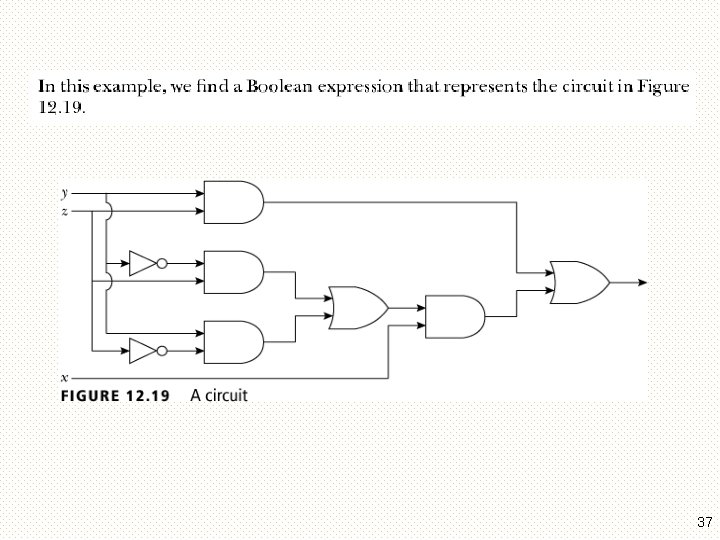
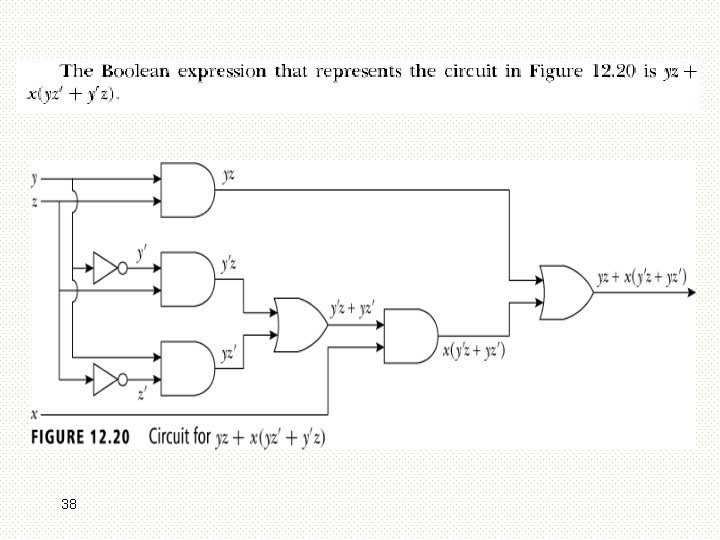
37

38

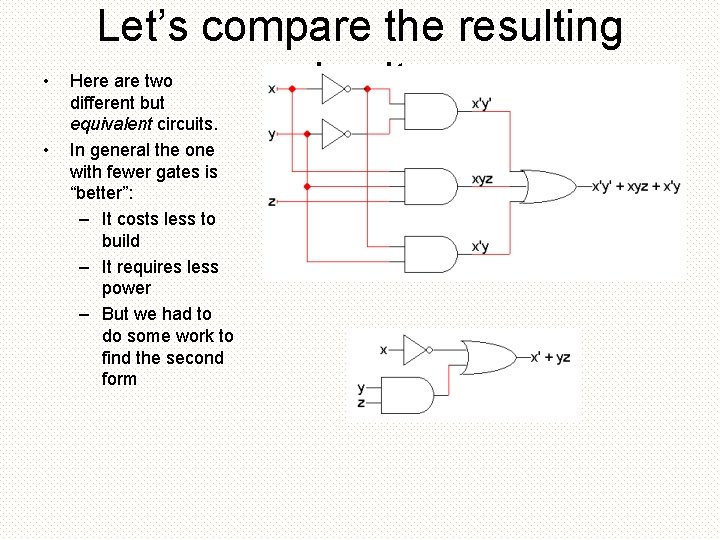
• • Let’s compare the resulting Here are two circuits different but equivalent circuits. In general the one with fewer gates is “better”: – It costs less to build – It requires less power – But we had to do some work to find the second form