CONTAGEM Aula de hoje Correo dos Exerccios Permutaes

CONTAGEM

Aula de hoje • Correção dos Exercícios • Permutações com Repetição • Combinações com Repetição • Permutações com Objetos Idênticos • Distribuição de Objetos em Caixas

Exercício 5 • Para fazer uma viagem Rio - São Paulo – Rio, posso usar como transporte o trem, o ônibus ou o avião. De quantos modos posso escolher os transportes se não desejo usar na volta o mesmo meio de transporte usado na ida? • Três meios de transporte

Exercício 5 • Ida (Rio – São Paulo) Posso ir de 3 formas diferentes

Exercício 5 • Ida (Rio – São Paulo) Posso ir de 3 formas diferentes • Volta (São Paulo - Rio) Posso voltar somente de 2 formas diferentes

Exercício 5 • Ida (Rio – São Paulo) Posso ir de 3 formas diferentes • Volta (São Paulo - Rio) Posso voltar somente de 2 formas diferentes Logo: 3 x 2 = 6 modos de se fazer a viagem.

Exercício 6 • Uma bandeira é formada por quatro listras, que devem ser coloridas usando se apenas as cores amarelo, branco e cinza, não devendo listras adjacentes ter a mesma cor. De quantos modos pode ser colorida a bandeira? 3 cores

Exercício 6 • Uma bandeira é formada por quatro listras, que devem ser coloridas usando se apenas as cores amarelo, branco e cinza, não devendo listras adjacentes ter a mesma cor. De quantos modos pode ser colorida a bandeira? Possibilidades para pintar 3 cores ? ? ? 3 cores

Exercício 6 • Uma bandeira é formada por quatro listras, que devem ser coloridas usando se apenas as cores amarelo, branco e cinza, não devendo listras adjacentes ter a mesma cor. De quantos modos pode ser colorida a bandeira? Possibilidades para pintar 3 cores 2 cores 3 cores

Exercício 6 • Uma bandeira é formada por quatro listras, que devem ser coloridas usando se apenas as cores amarelo, branco e cinza, não devendo listras adjacentes ter a mesma cor. De quantos modos pode ser colorida a bandeira? Possibilidades para pintar 3 cores 2 cores Total = 24 cores 3 cores

Exercício 7 • Quantos números naturais de três algarismos distintos (na base 10) existe? 0 1 2 3 4 5 6 7 8 9 base 10

Exercício 7 • Quantos números naturais de três algarismos distintos (na base 10) existe? 0 1 2 3 4 5 6 7 8 9 base 10 _________

Exercício 7 • Quantos números naturais de três algarismos distintos (na base 10) existe? 0 1 2 3 4 5 6 7 8 9 base 10 ____9____? _____ Não pode ser o 0 ____? ______

Exercício 7 • Quantos números naturais de três algarismos distintos (na base 10) existe? 0 1 2 3 4 5 6 7 8 9 base 10 ____9_____? ______ Deve ser distinto

Exercício 7 • Quantos números naturais de três algarismos distintos (na base 10) existe? 0 1 2 3 4 5 6 7 8 9 base 10 ____9_____ Deve ser distinto ____8______

Exercício 7 • Quantos números naturais de três algarismos distintos (na base 10) existe? 0 1 2 3 4 5 6 7 8 9 base 10 ____9_____ = 648 ____8______

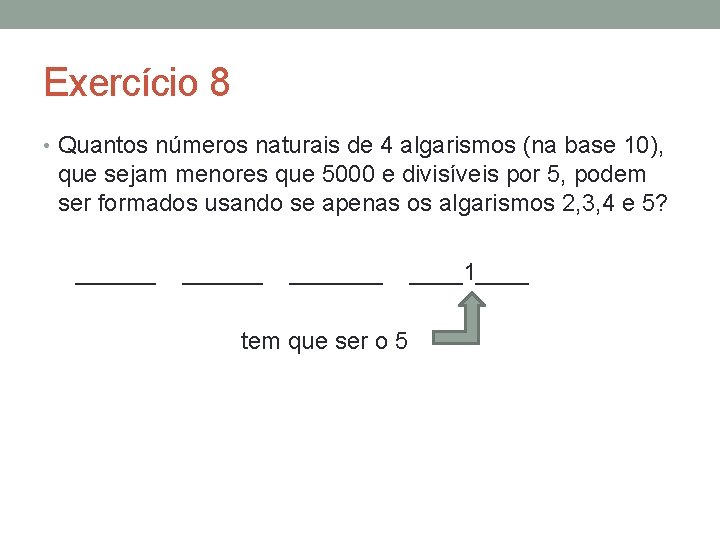
Exercício 8 • Quantos números naturais de 4 algarismos (na base 10), que sejam menores que 5000 e divisíveis por 5, podem ser formados usando se apenas os algarismos 2, 3, 4 e 5? _______ ____? ____ quantos são possíveis aqui?

Exercício 8 • Quantos números naturais de 4 algarismos (na base 10), que sejam menores que 5000 e divisíveis por 5, podem ser formados usando se apenas os algarismos 2, 3, 4 e 5? _______ tem que ser o 5 ____1____

Exercício 8 • Quantos números naturais de 4 algarismos (na base 10), que sejam menores que 5000 e divisíveis por 5, podem ser formados usando se apenas os algarismos 2, 3, 4 e 5? _______ ____1____ Quantos são possíveis aqui?

Exercício 8 • Quantos números naturais de 4 algarismos (na base 10), que sejam menores que 5000 e divisíveis por 5, podem ser formados usando se apenas os algarismos 2, 3, 4 e 5? __3___ _______1____ Não pode ser o 5

Exercício 8 • Quantos números naturais de 4 algarismos (na base 10), que sejam menores que 5000 e divisíveis por 5, podem ser formados usando se apenas os algarismos 2, 3, 4 e 5? __3___ ___? ____1____ Quantos são possíveis aqui?

Exercício 8 • Quantos números naturais de 4 algarismos (na base 10), que sejam menores que 5000 e divisíveis por 5, podem ser formados usando se apenas os algarismos 2, 3, 4 e 5? __3___ ___4____1____ Total de 48 modos!!!

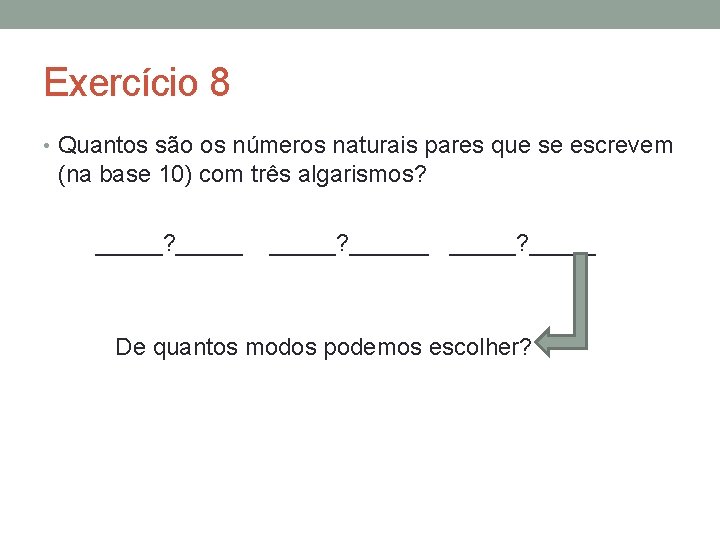
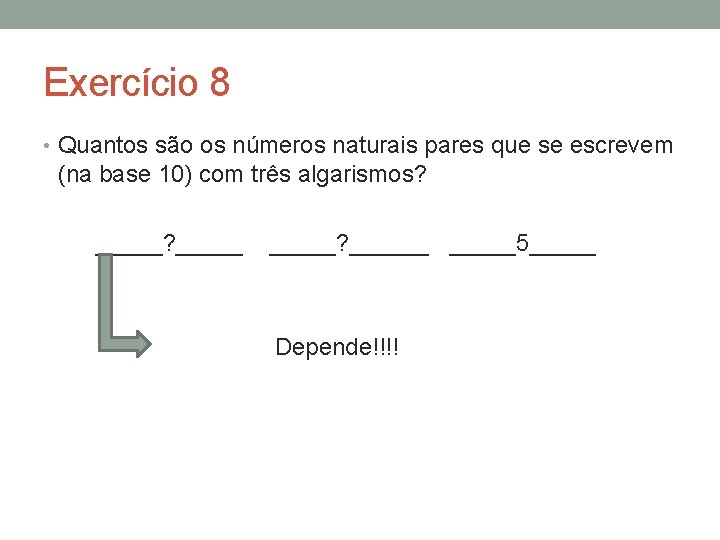
Exercício 8 • Quantos são os números naturais pares que se escrevem (na base 10) com três algarismos? _____? ______? _____ De quantos modos podemos escolher?

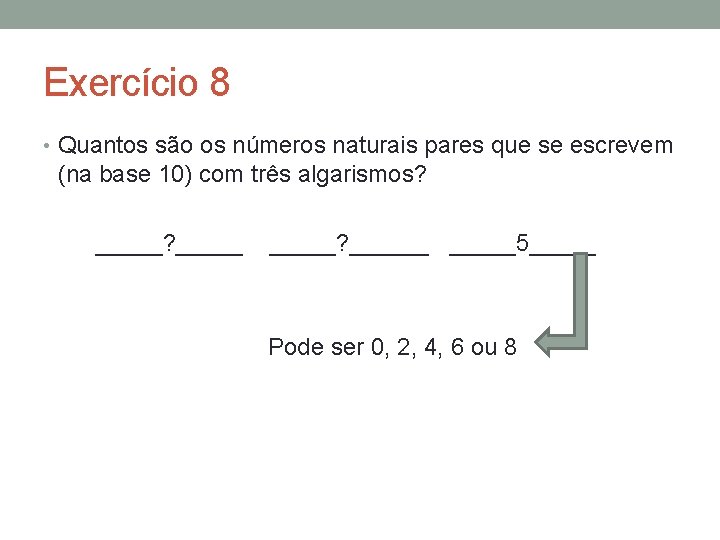
Exercício 8 • Quantos são os números naturais pares que se escrevem (na base 10) com três algarismos? _____? ______5_____ Pode ser 0, 2, 4, 6 ou 8

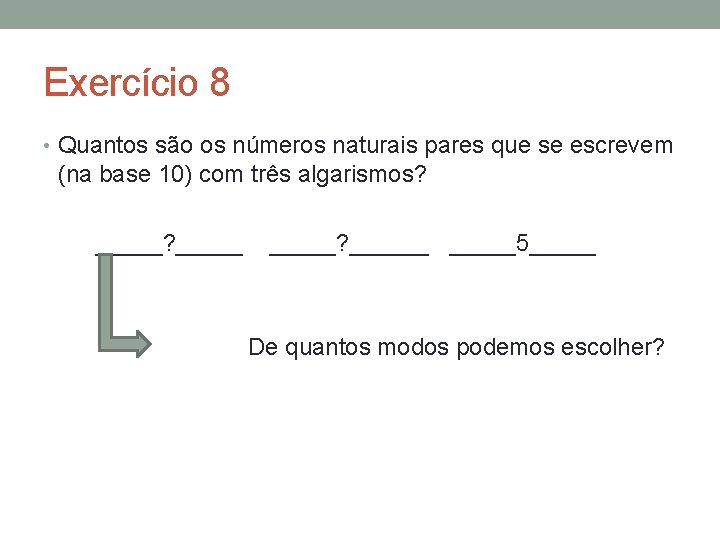
Exercício 8 • Quantos são os números naturais pares que se escrevem (na base 10) com três algarismos? _____? ______5_____ De quantos modos podemos escolher?

Exercício 8 • Quantos são os números naturais pares que se escrevem (na base 10) com três algarismos? _____? ______5_____ Depende!!!!

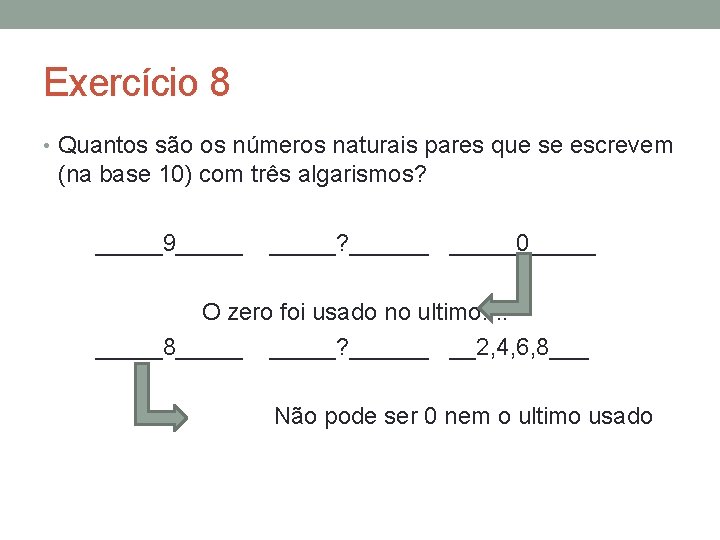
Exercício 8 • Quantos são os números naturais pares que se escrevem (na base 10) com três algarismos? _____9_____? ______0_____ O zero foi usado no ultimo!!!! _____8_____? ______ __2, 4, 6, 8___ Não pode ser 0 nem o ultimo usado

Exercício 8 • Quantos são os números naturais pares que se escrevem (na base 10) com três algarismos? • Caso 1) Termina com 0 _____9_____8______1_____ • Caso 2) Não termina com 0 _____8______4_____

Exercício 8 • Quantos são os números naturais pares que se escrevem (na base 10) com três algarismos? • Caso 1) Termina com 0 = 72 números _____9_____8______1_____ • Caso 2) Não termina com 0 = 256 números _____8______4_____ Total = 72 + 256 = 328

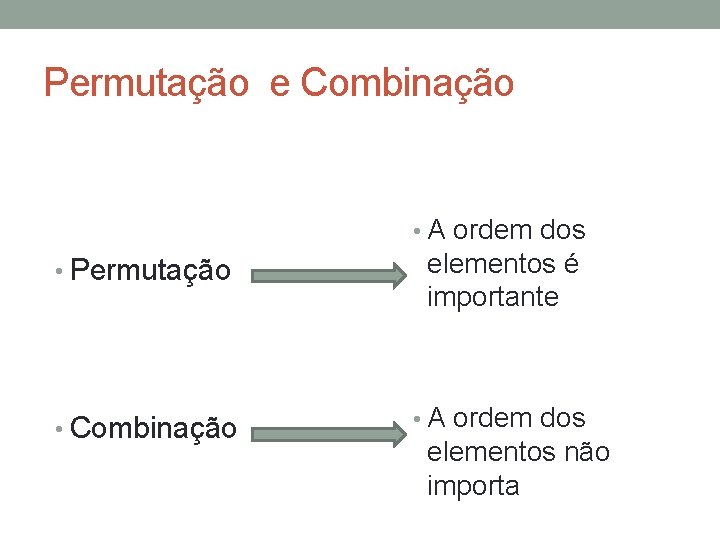
Permutação e Combinação • A ordem dos • Permutação ? • Combinação elementos é importante • A ordem dos elementos não importa

Permutação e Combinação • A ordem dos • Permutação elementos é importante • Combinação • A ordem dos elementos não importa

Pergunta? • Quantas palavras de extensão 3 podem ser formadas com 26 letras? • Distintas: ____26____25____24____ P(26, 3) = 26! / (26 -3)!

Pergunta? • Quantas palavras de extensão 3 podem ser formadas com 26 letras? • Distintas: ____26____25____24____ P(26, 3) = 26! / (26 -3)! • Repetidas: ____? ____

Pergunta? • Quantas palavras de extensão 3 podem ser formadas com 26 letras? • Distintas: ____26____25____24____ P(26, 3) = 26! / (26 -3)! • Repetidas: ____26____ 263

Permutações com Repetição • Quantas palavras de extensão 3 podem ser formadas com 26 letras? • Distintas: P(n, r) = n! / (n-r)! • Repetidas: • O número de r-permutações de um conjunto com n objetos, com repetição, é nr

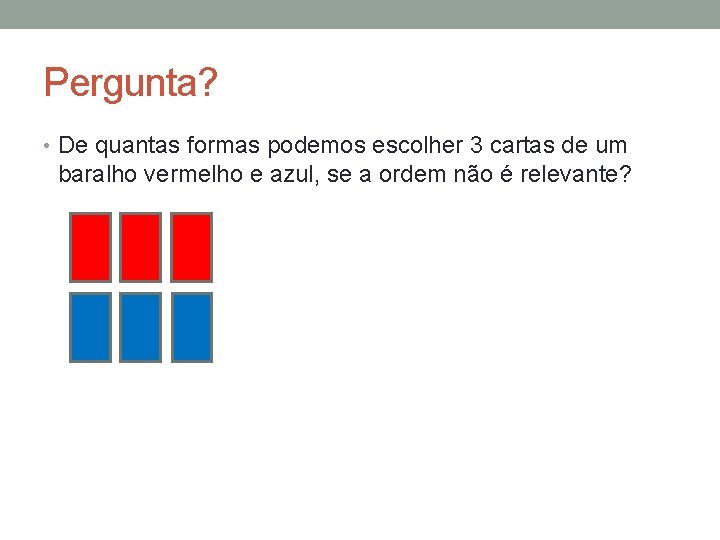
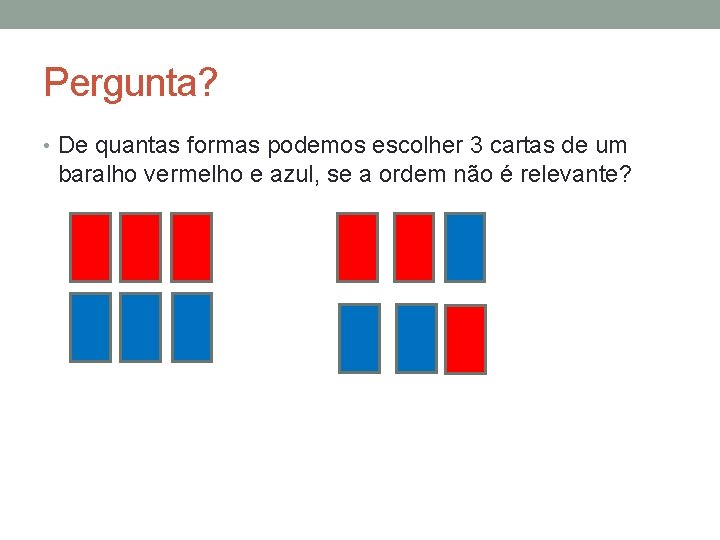
Pergunta? • De quantas formas podemos escolher 3 cartas de um baralho vermelho e azul, se a ordem não é relevante?

Pergunta? • De quantas formas podemos escolher 3 cartas de um baralho vermelho e azul, se a ordem não é relevante?

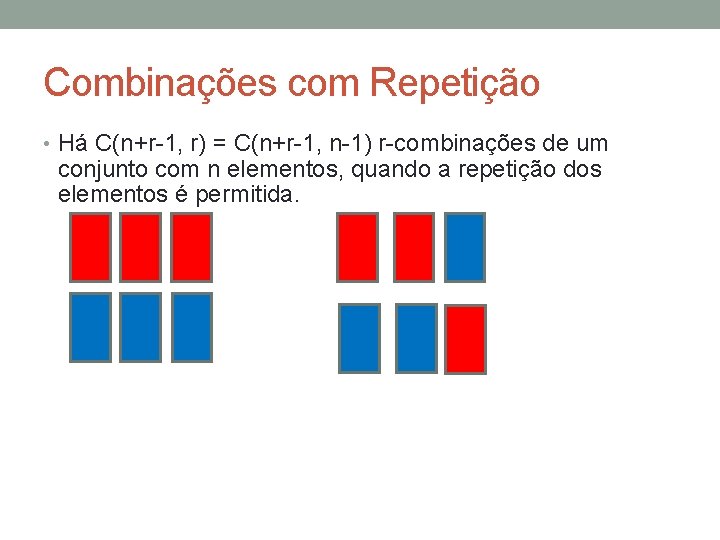
Combinações com Repetição • Há C(n+r-1, r) = C(n+r-1, n-1) r-combinações de um conjunto com n elementos, quando a repetição dos elementos é permitida.

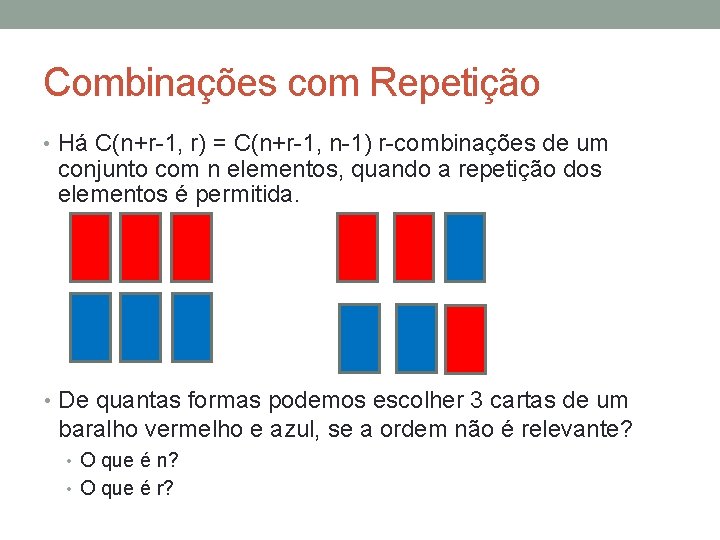
Combinações com Repetição • Há C(n+r-1, r) = C(n+r-1, n-1) r-combinações de um conjunto com n elementos, quando a repetição dos elementos é permitida. • De quantas formas podemos escolher 3 cartas de um baralho vermelho e azul, se a ordem não é relevante? • O que é n? • O que é r?

Combinações com Repetição • Há C(n+r-1, r) = C(n+r-1, n-1) r-combinações de um conjunto com n elementos, quando a repetição dos elementos é permitida. • De quantas formas podemos escolher 3 cartas de um baralho vermelho e azul, se a ordem não é relevante? • n são as possíveis escolhas (2 cores) • r é o numero de cartas a serem escolhidas (3)

Combinações com Repetição • Há C(n+r-1, r) = C(n+r-1, n-1) r-combinações de um conjunto com n elementos, quando a repetição dos elementos é permitida. • C(2+3 -1, 3) = C(4, 3) = 4

Pergunta • Há quantas maneiras possíveis de escolher quatro pedaços de fruta a partir de uma tigela que contém maçãs, laranjas e pêras, se a ordem em que cada pedaço é escolhido não é relevante, apenas o tipo da fruta, e o pedaço individual não é relevante também, sendo que há pelo menos 4 pedaços de cada tipo de fruta na tigela?

Pergunta • Há quantas maneiras possíveis de escolher quatro pedaços de fruta a partir de uma tigela que contém maçãs, laranjas e pêras, se a ordem em que cada pedaço é escolhido não é relevante, apenas o tipo da fruta, e o pedaço individual não é relevante também, sendo que há pelo menos 4 pedaços de cada tipo de fruta na tigela? COMBINAÇÃO

Pergunta • Há quantas maneiras possíveis de escolher quatro pedaços de fruta a partir de uma tigela que contém maçãs, laranjas e pêras, se a ordem em que cada pedaço é escolhido não é relevante, apenas o tipo da fruta, e o pedaço individual não é relevante também, sendo que há pelo menos 4 pedaços de cada tipo de fruta na tigela? C(n+r-1, r) = C(? , ? )

Pergunta • Há quantas maneiras possíveis de escolher quatro pedaços de fruta a partir de uma tigela que contém maçãs, laranjas e pêras, se a ordem em que cada pedaço é escolhido não é relevante, apenas o tipo da fruta, e o pedaço individual não é relevante também, sendo que há pelo menos 4 pedaços de cada tipo de fruta na tigela? C(n+r-1, r) = C(3+4 -1, 4)

Pergunta • Há quantas maneiras possíveis de escolher quatro pedaços de fruta a partir de uma tigela que contém maçãs, laranjas e pêras, se a ordem em que cada pedaço é escolhido não é relevante, apenas o tipo da fruta, e o pedaço individual não é relevante também, sendo que há pelo menos 4 pedaços de cada tipo de fruta na tigela? C(n+r-1, r) = C(3+4 -1, 4) = = C(6, 4) = 6 x 5 / 2 = 15

Pergunta

Exercício 10 • Quantos são os anagramas de PRATICO?

Exercício 10 • Quantos são os anagramas de PRATICO? P(7, 7) = 7!

Pergunta • Quantos são os anagramas de PRATICO? P(7, 7) = 7! • Quantos são os anagramas de SUCCESS?

Pergunta • Quantos são os anagramas de PRATICO? P(7, 7) = 7! • Quantos são os anagramas de SUCCESS? • Como algumas letras de SUCCESS são idênticas, não será considerado o número de permutações de 7 letras. 3 S ´s 2 C ´s 1 Ue 1 E

Permutações com objetos idênticos • Quantos são os anagramas de PRATICO? P(7, 7) = 7! • Quantos são os anagramas de SUCCESS? • Como algumas letras de SUCCESS são idênticas, não será considerado o número de permutações de 7 letras. 3 S ´s podem ser colocados em 7 posições C(7, 3) 2 C ´s 1 Ue 1 E

Permutações com objetos idênticos • Quantos são os anagramas de PRATICO? P(7, 7) = 7! • Quantos são os anagramas de SUCCESS? • Como algumas letras de SUCCESS são idênticas, não será considerado o número de permutações de 7 letras. 3 S ´s 2 C ´s 1 U 1 E podem ser colocados em 7 posições C(7, 3) podem ser colocados em 4 posições C(4, 2) C(2, 1) C(1, 1)

Permutações com objetos idênticos • Quantos são os anagramas de PRATICO? P(7, 7) = 7! • Quantos são os anagramas de SUCCESS? • Como algumas letras de SUCCESS são idênticas, não será considerado o número de permutações de 7 letras. 3 S ´s podem ser colocados em 7 posições C(7, 3) 2 C ´s podem ser colocados em 4 posições C(4, 2) 1 U C(2, 1) 1 E C(1, 1) = C(7, 3)x. C(4, 2)x. C(2, 1)x. C(1, 1) = 420

Permutações com objetos idênticos • Quantos são os anagramas de SUCCESS? 3 S ´s podem ser colocados em 7 posições C(7, 3) 2 C ´s podem ser colocados em 4 posições C(4, 2) 1 U C(2, 1) 1 E C(1, 1) = C(7, 3)x. C(4, 2)x. C(2, 1)x. C(1, 1) = 420 = 7! / 3! x 2! x 1! Teorema? !!

Permutações com objetos idênticos • Quantos são os anagramas de SUCCESS? = C(7, 3)x. C(4, 2)x. C(2, 1)x. C(1, 1) = 420 = 7! / 3! x 2! x 1! O número de permutações diferentes de n objetos, em que há n 1 objetos idênticos do tipo 1, n 2 objetos idênticos do tipo 2, . . . E nk objetos idênticos do tipo k, é n! n 1! n 2!. . . nk!