Computer Graphics 1 Last Updated 13 Jan12 Linear

















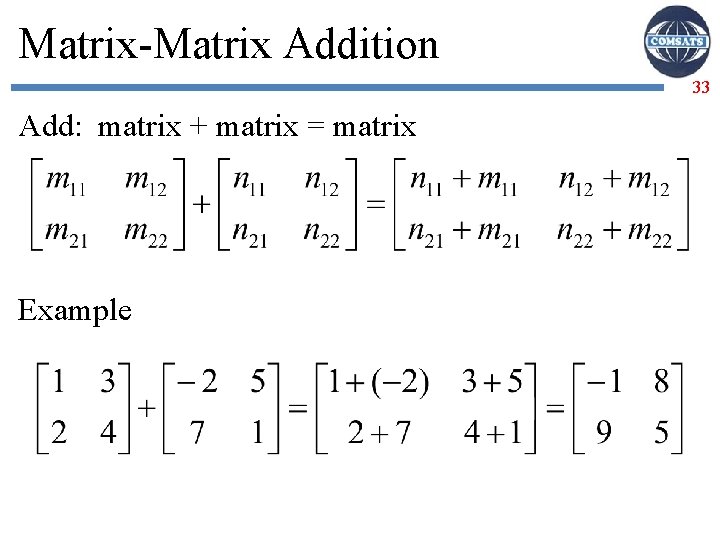














- Slides: 48

Computer Graphics 1 Last Updated: 13 -Jan-12 Linear Algebra (Mathematics for CG) Reading: HB Appendix A

Notation: Scalars, Vectors, Matrices 2 Scalar Ø (lower case, italic) Vector Ø (lower case, bold) Matrix Ø (upper case, bold)

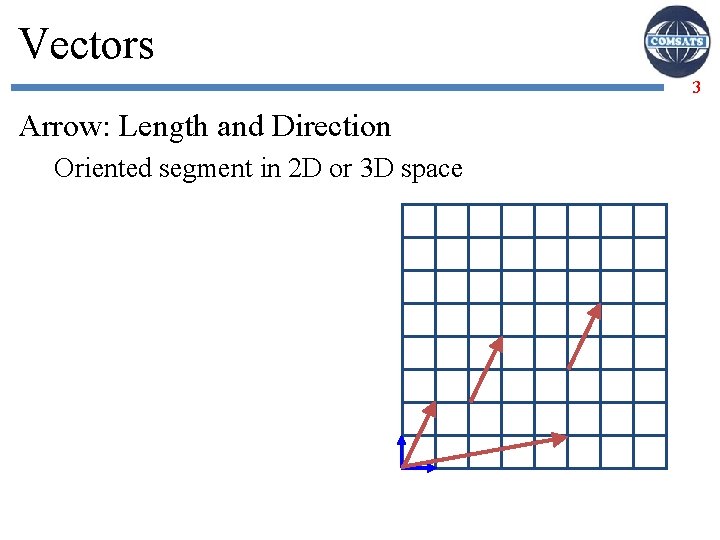
Vectors 3 Arrow: Length and Direction Oriented segment in 2 D or 3 D space

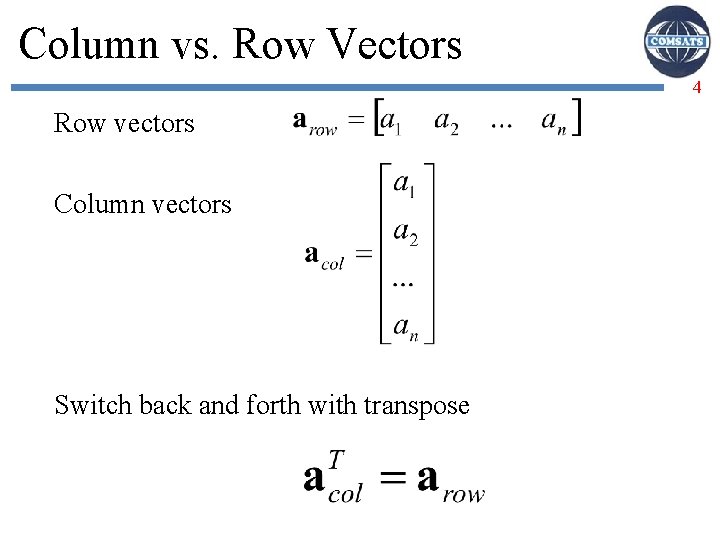
Column vs. Row Vectors 4 Row vectors Column vectors Switch back and forth with transpose

Vector-Vector Addition 5 Add: vector + vector = vector Parallelogram rule tail to head, complete the triangle geometric examples: algebraic

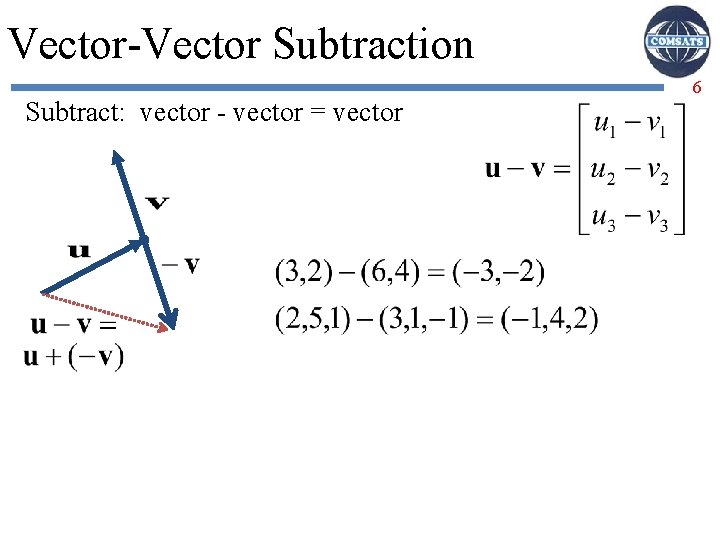
Vector-Vector Subtraction Subtract: vector - vector = vector 6

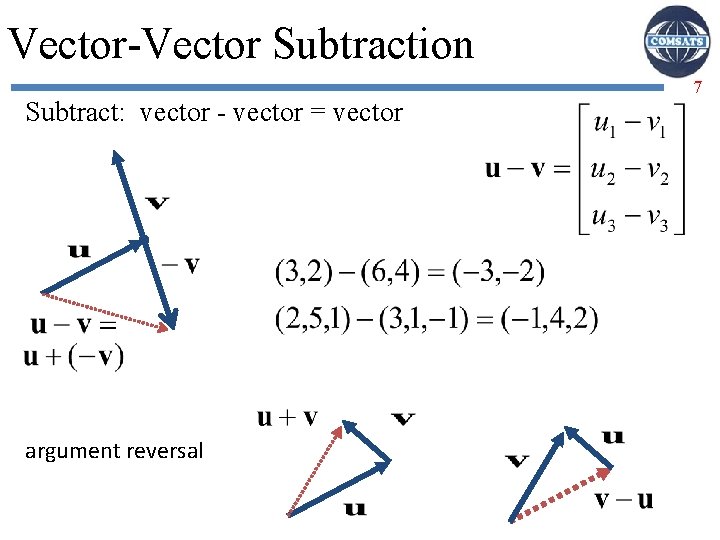
Vector-Vector Subtraction Subtract: vector - vector = vector argument reversal 7

Scalar-Vector Multiplication Multiply: scalar * vector = vector is scaled 8

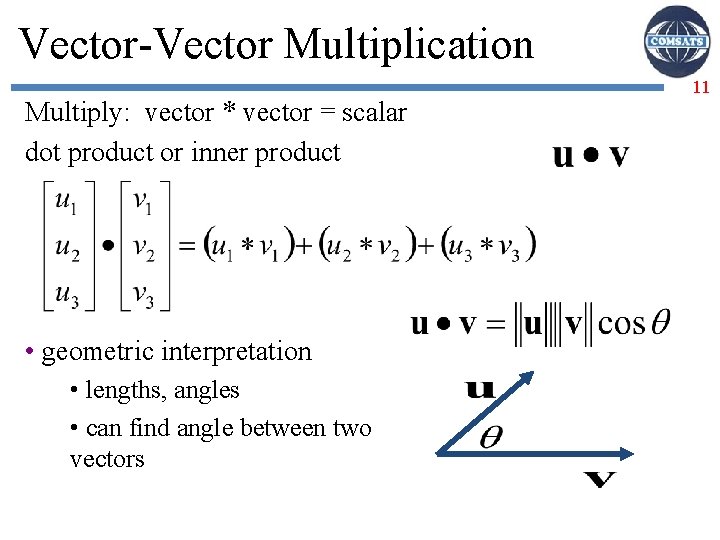
Vector-Vector Multiplication Multiply: vector * vector = scalar Dot product or Inner product 9

Vector-Vector Multiplication Multiply: vector * vector = scalar dot product, aka inner product 10

Vector-Vector Multiplication Multiply: vector * vector = scalar dot product or inner product • geometric interpretation • lengths, angles • can find angle between two vectors 11

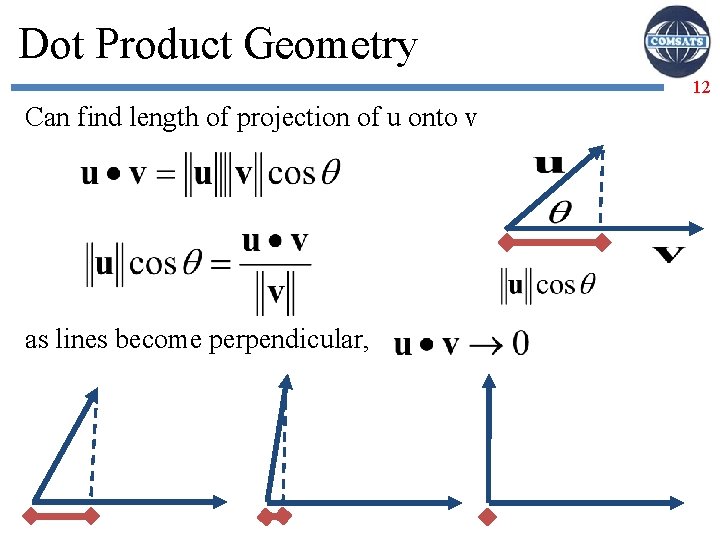
Dot Product Geometry 12 Can find length of projection of u onto v as lines become perpendicular,

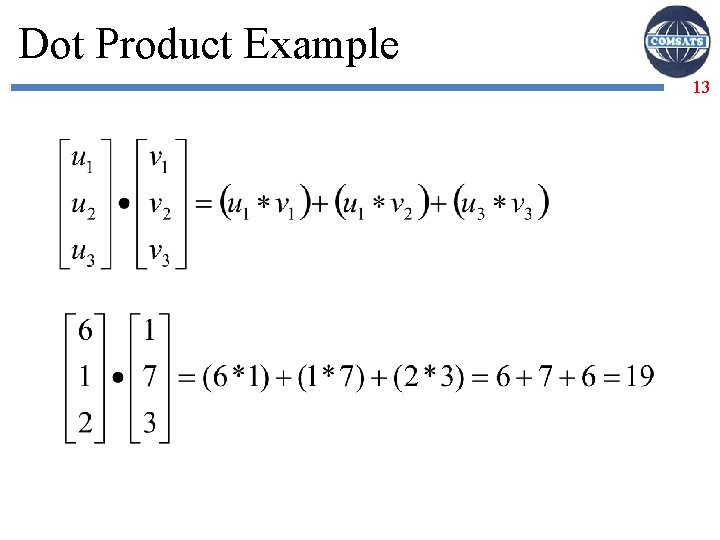
Dot Product Example 13

Vector-Vector Multiplication 14 Multiply: vector * vector = vector cross product

Vector-Vector Multiplication multiply: vector * vector = vector cross product algebraic geometric parallelogram area perpendicular to parallelogram 15

RHS vs. LHS Coordinate Systems 16 Right-handed coordinate system right hand rule: index finger x, second finger y; right thumb points up Left-handed coordinate system left hand rule: index finger x, second finger y; left thumb points down

Basis Vectors Take any two vectors that are linearly independent (nonzero and nonparallel) can use linear combination of these to define any other vector: 17

Orthonormal Basis Vectors 18 If basis vectors are orthonormal (orthogonal (mutually perpendicular) and unit length) o we have Cartesian coordinate system o familiar Pythagorean definition of distance Orthonormal algebraic properties

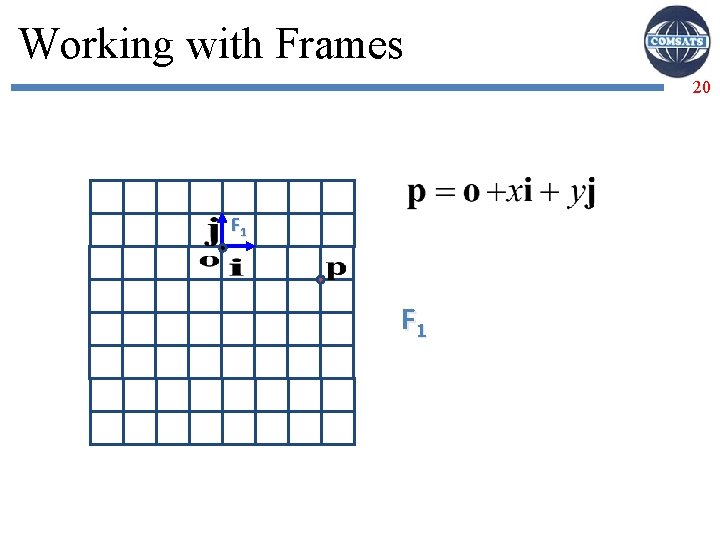
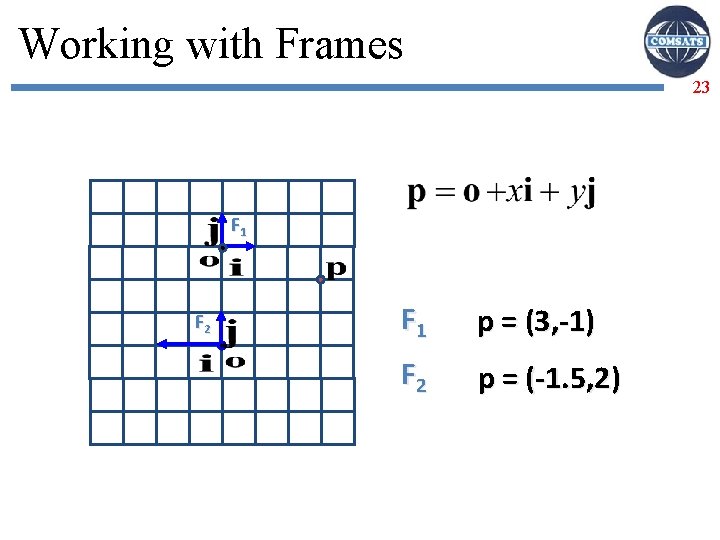
Basis Vectors and Origins 19 Coordinate system: just basis vectors can only specify offset: vectors Coordinate frame (or Frame of Reference): basis vectors and origin can specify location as well as offset: points It helps in analyzing the vectors and solving the kinematics.

Working with Frames 20 F 1

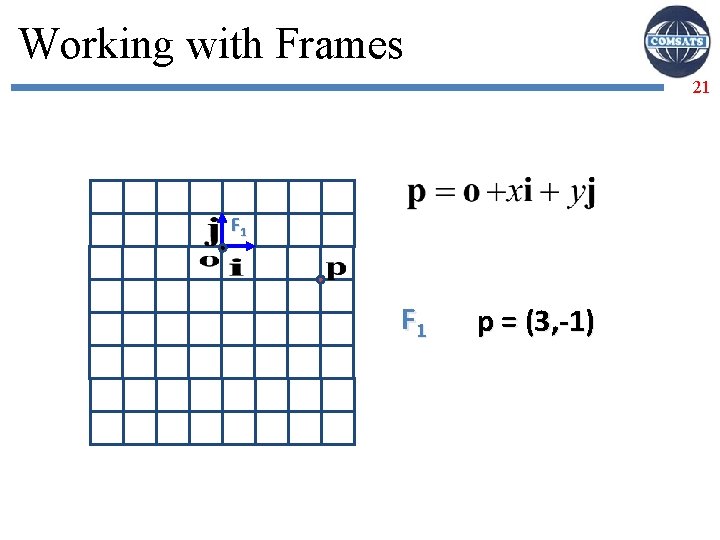
Working with Frames 21 F 1 p = (3, -1)

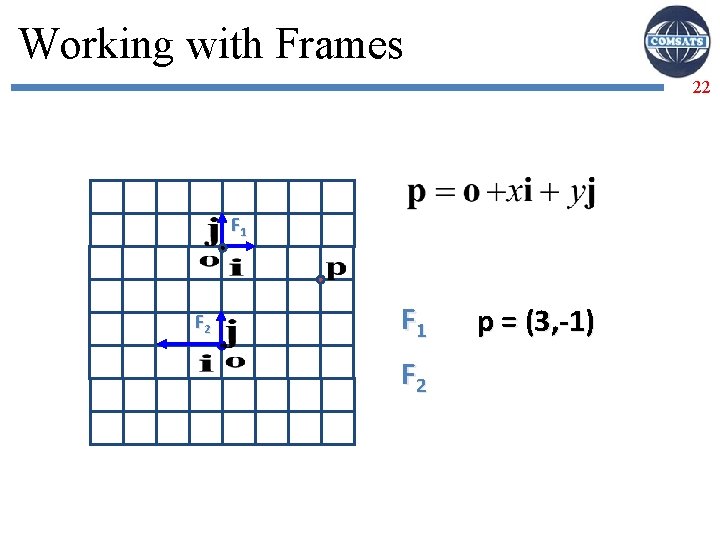
Working with Frames 22 F 1 F 2 p = (3, -1)

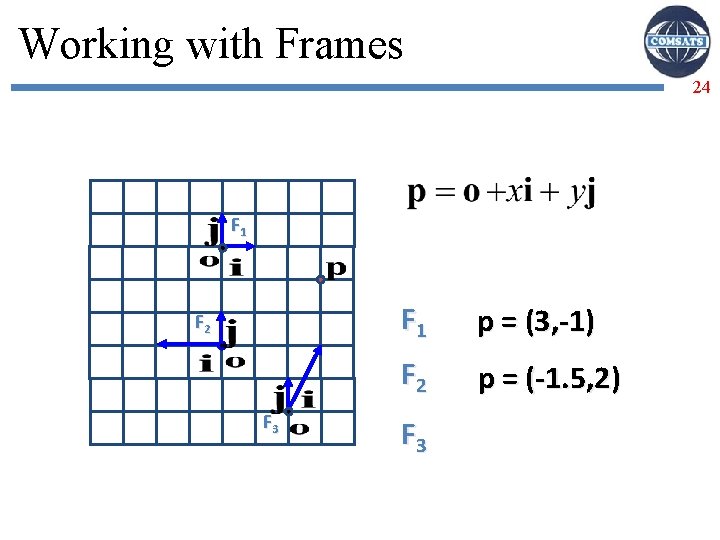
Working with Frames 23 F 1 F 2 F 1 p = (3, -1) F 2 p = (-1. 5, 2)

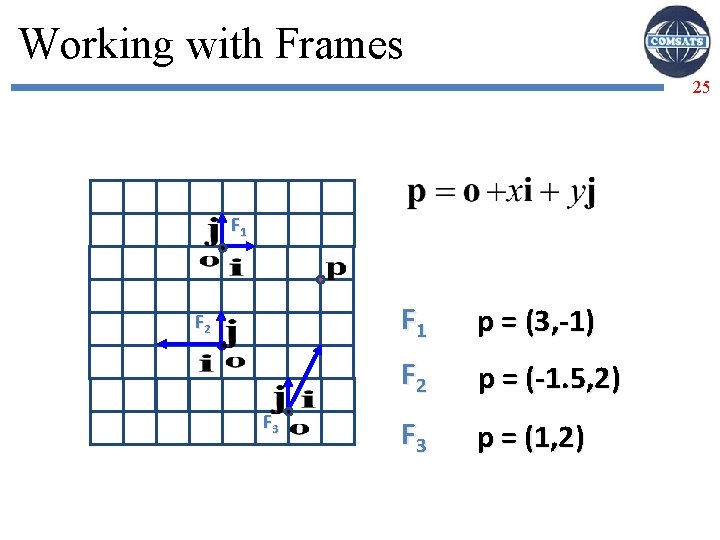
Working with Frames 24 F 1 F 2 F 3 F 1 p = (3, -1) F 2 p = (-1. 5, 2) F 3

Working with Frames 25 F 1 F 2 F 3 F 1 p = (3, -1) F 2 p = (-1. 5, 2) F 3 p = (1, 2)

Named Coordinate Frames 26 Origin and basis vectors Pick canonical frame of reference Ø then don’t have to store origin, basis vectors Ø just Ø convention: Cartesian orthonormal one on previous slide Handy to specify others as needed Ø airplane nose, looking over your shoulder, . . . Ø really common ones given names in CG vobject, world, camera, screen, . . .

Lines 27 Slope-intercept form y = mx + b Implicit form y – mx – b = 0 Ax + By + C = 0 f(x, y) = 0

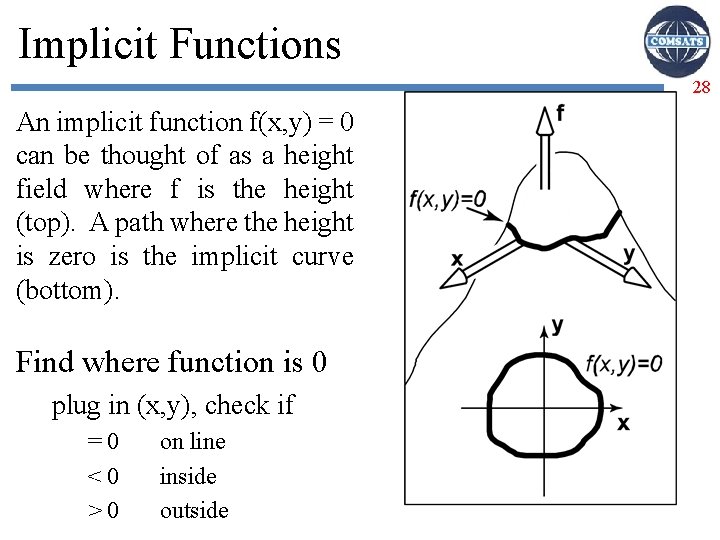
Implicit Functions 28 An implicit function f(x, y) = 0 can be thought of as a height field where f is the height (top). A path where the height is zero is the implicit curve (bottom). Find where function is 0 plug in (x, y), check if =0 <0 >0 on line inside outside

Implicit Circles 29 circle is points (x, y) where f(x, y) = 0 points p on circle have property that vector from c to p dotted with itself has value r 2 points p on the circle have property that squared distance from c to p is r 2 points p on circle are those a distance r from center point c

Parametric Curves 30 Parameter: index that changes continuously (x, y): point on curve t: parameter Vector form

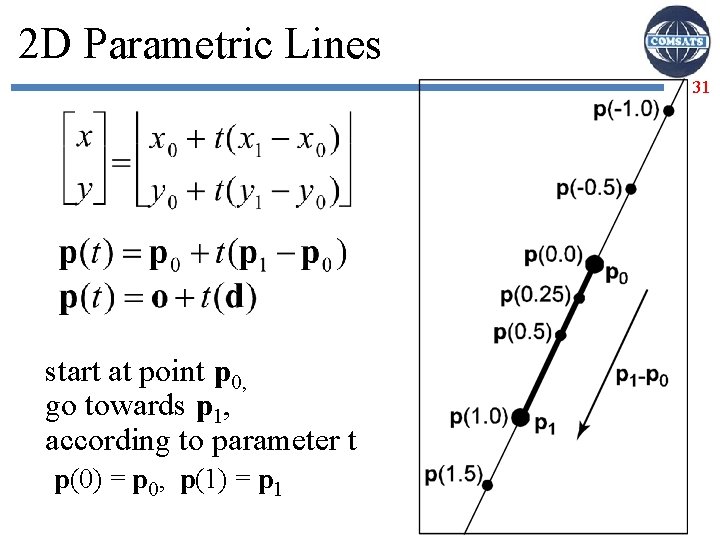
2 D Parametric Lines 31 start at point p 0, go towards p 1, according to parameter t p(0) = p 0, p(1) = p 1

Linear Interpolation 32 Parametric line is example of general concept Interpolation p goes through a at t = 0 p goes through b at t = 1 Linear weights t, (1 -t) are linear polynomials in t
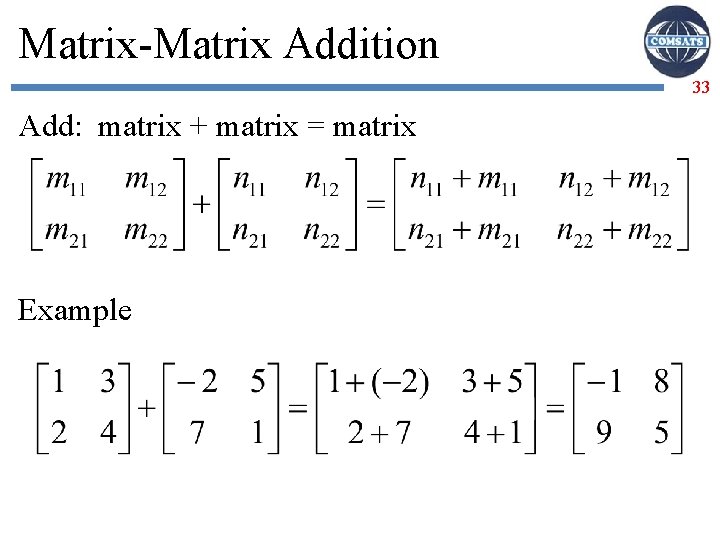
Matrix-Matrix Addition 33 Add: matrix + matrix = matrix Example

Scalar-Matrix Multiplication 34 Multiply: scalar * matrix = matrix Example

Matrix-Matrix Multiplication 35 Can only multiply (n, k) by (k, m): number of left cols = number of right rows legal undefined

Matrix-Matrix Multiplication 36 row by column

Matrix-Matrix Multiplication 37 row by column

Matrix-Matrix Multiplication 38 row by column

Matrix-Matrix Multiplication 39 row by column

Matrix-Matrix Multiplication 40 row by column Non commutative: AB != BA

Matrix-Vector Multiplication points as column vectors: post-multiply 41

Matrices 42 Transpose Identity Inverse

Matrices and Linear Systems 43 Linear system of n equations, n unknowns Matrix form Ax=b

Exercise 1 44 Q 1: If the vectors, u and v in figure are coplanar with the sheet of paper, does the cross product v x u extend towards the reader or away assuming right-handed coordinate system? For u = [1, 0, 0] & v = [2, 2, 1]. Find Q 2: The length of v Q 3: length of projection of u onto v Q 4: v x u Q 5: Cos t, if t is the angle between u & v

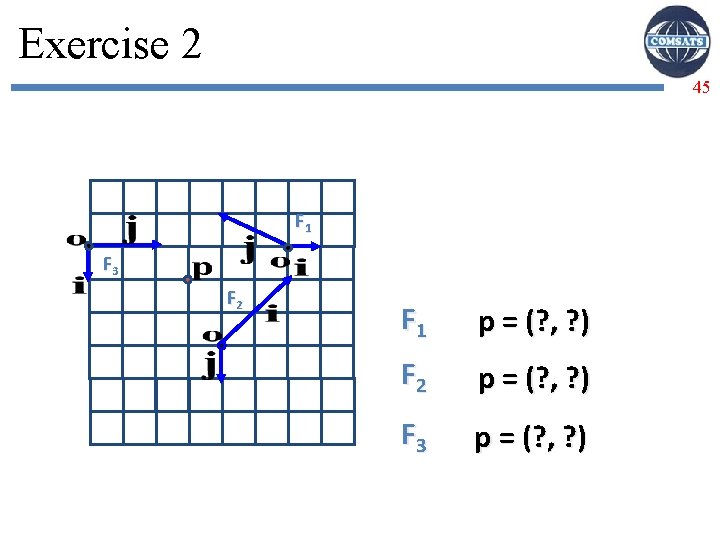
Exercise 2 45 F 1 F 3 F 2 F 1 p = (? , ? ) F 2 p = (? , ? ) F 3 p = (? , ? )

Exercise 3 46 Given P 1(3, 6, 9) and P 2(5, 5, 5). Find a point on the line with end points P 1 & P 2 at t = 2/3 using parametric equation of line, where t is the parameter.

Things to do 47 Reading for Open. GL practice: HB 2. 9 Ready for the Quiz

References 48 1. 2. http: //faculty. cs. tamu. edu/schaefer/teaching/441_Spring 2012/index. html http: //www. ugrad. cs. ubc. ca/~cs 314/Vjan 2007/
 Graphics monitors and workstations and input devices
Graphics monitors and workstations and input devices Introduction to computer graphics - ppt
Introduction to computer graphics - ppt The symbol tsfa in alu operations include
The symbol tsfa in alu operations include Performance monitoring and review form
Performance monitoring and review form Difference between linear and non linear pipeline
Difference between linear and non linear pipeline Angel computer graphics
Angel computer graphics Define viewing in computer graphics
Define viewing in computer graphics Plasma display in computer graphics
Plasma display in computer graphics Two dimensional viewing
Two dimensional viewing Shear transformation in computer graphics
Shear transformation in computer graphics Shader computer graphics
Shader computer graphics Scan converting ellipse in computer graphics
Scan converting ellipse in computer graphics Rigid body transformation in computer graphics
Rigid body transformation in computer graphics Region filling process has application in
Region filling process has application in Starburst method
Starburst method Polygon filling algorithm
Polygon filling algorithm In random scan display, the frame buffer holds …
In random scan display, the frame buffer holds … Computer graphics
Computer graphics Incremental algorithm in computer graphics
Incremental algorithm in computer graphics Cs 418
Cs 418 Cs 418 interactive computer graphics
Cs 418 interactive computer graphics Depth sorting method in computer graphics
Depth sorting method in computer graphics Achromatic light in computer graphics
Achromatic light in computer graphics Interactive input
Interactive input Uniform scaling in computer graphics
Uniform scaling in computer graphics Uniform scaling in computer graphics
Uniform scaling in computer graphics Fundamentals of computer graphics
Fundamentals of computer graphics Logical input devices in computer graphics
Logical input devices in computer graphics Fundamentals of computer graphics
Fundamentals of computer graphics Points and lines in computer graphics ppt
Points and lines in computer graphics ppt Dda algorithm in computer graphics ppt
Dda algorithm in computer graphics ppt Differential line algorithm in computer graphics
Differential line algorithm in computer graphics Normalized device coordinate
Normalized device coordinate Csc418
Csc418 Sweep representation in computer graphics
Sweep representation in computer graphics Scan conversion in computer graphics
Scan conversion in computer graphics Region filling and clipping in computer graphics
Region filling and clipping in computer graphics Utah teapot vertex data
Utah teapot vertex data Thick primitives in computer graphics
Thick primitives in computer graphics Interaction in computer graphics
Interaction in computer graphics Hierarchical modeling in computer graphics
Hierarchical modeling in computer graphics Rendering pipeline in computer graphics
Rendering pipeline in computer graphics Scan conversion of ellipse in computer graphics
Scan conversion of ellipse in computer graphics Srgp in computer graphics
Srgp in computer graphics Computer graphics transformation matrix
Computer graphics transformation matrix Gupta sproull algorithm
Gupta sproull algorithm Uniform scaling in computer graphics
Uniform scaling in computer graphics Computer
Computer Input techniques in computer graphics
Input techniques in computer graphics