Computer Graphics Lecture 3 Line Circle Drawing Computer

Computer Graphics Lecture 3 Line & Circle Drawing

Computer Graphics Towards the Ideal Line • We can only do a discrete approximation • Illuminate pixels as close to the true path as possible, consider bi-level display only – Pixels are either lit or not lit

Computer Graphics What is an ideal line • Must appear straight and continuous o – Only possible axis-aligned and 45 lines • Must interpolate both defining end points • Must have uniform density and intensity – Consistent within a line and over all lines – What about antialiasing? • Must be efficient, drawn quickly – Lots of them are required!!!

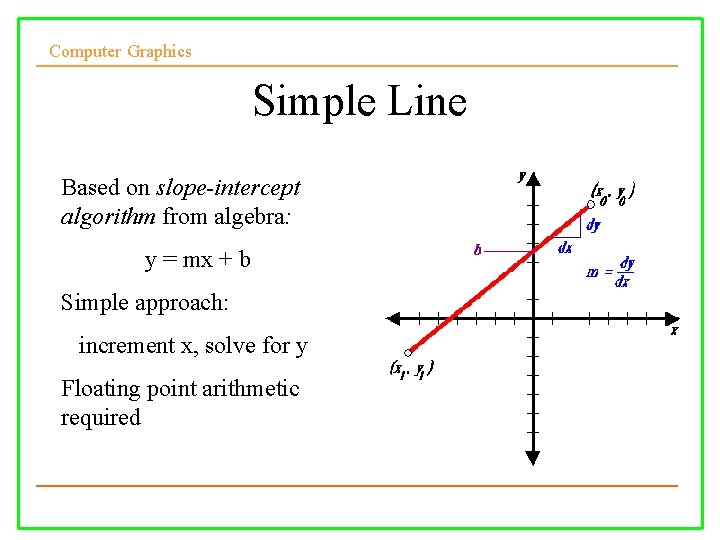
Computer Graphics Simple Line Based on slope-intercept algorithm from algebra: y = mx + b Simple approach: increment x, solve for y Floating point arithmetic required

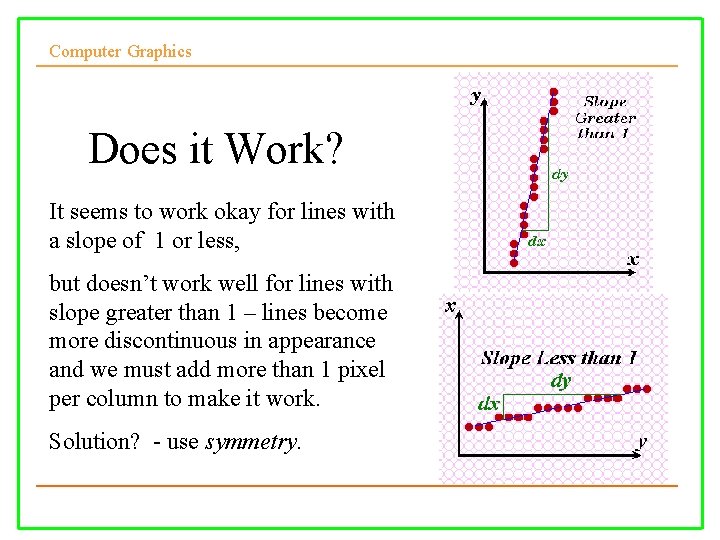
Computer Graphics Does it Work? It seems to work okay for lines with a slope of 1 or less, but doesn’t work well for lines with slope greater than 1 – lines become more discontinuous in appearance and we must add more than 1 pixel per column to make it work. Solution? - use symmetry.

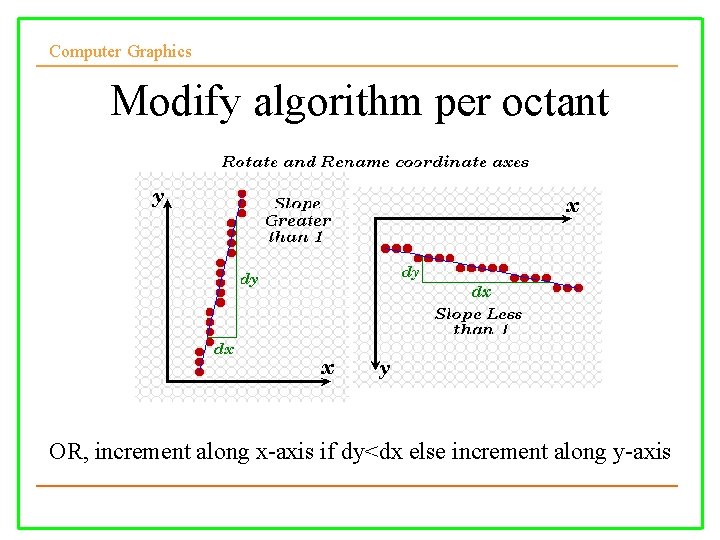
Computer Graphics Modify algorithm per octant OR, increment along x-axis if dy<dx else increment along y-axis

Computer Graphics DDA algorithm • DDA = Digital Differential Analyser – finite differences • Treat line as parametric equation in t : Start point End point -

Computer Graphics DDA Algorithm • • Start at t = 0 At each step, increment t by dt Choose appropriate value for dt Ensure no pixels are missed: – Implies: and • Set dt to maximum of dx and dy

Computer Graphics DDA algorithm line(int x 1, int y 1, int x 2, int y 2) { float x, y; int dx = x 2 -x 1, dy = y 2 -y 1; int n = max(abs(dx), abs(dy)); float dt = n, dxdt = dx/dt, dydt = dy/dt; x = x 1; y = y 1; while( n-- ) { point(round(x), round(y)); x += dxdt; y += dydt; } } n - range of t.

Computer Graphics DDA algorithm • Still need a lot of floating point arithmetic. – 2 ‘round’s and 2 adds per pixel. • Is there a simpler way ? • Can we use only integer arithmetic ? – Easier to implement in hardware.

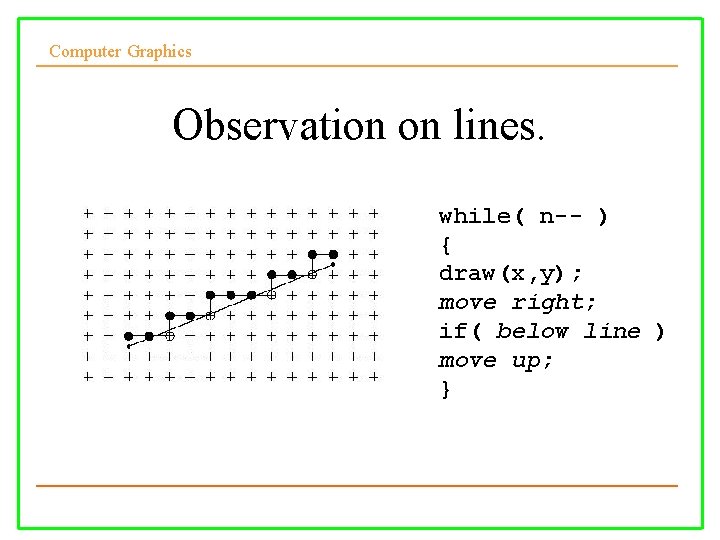
Computer Graphics Observation on lines. while( n-- ) { draw(x, y); move right; if( below line ) move up; }

Computer Graphics Testing for the side of a line. • Need a test to determine which side of a line a pixel lies. • Write the line in implicit form: • If (b<0) F<0 for points above the line, F>0 for points below.

Computer Graphics Testing for the side of a line. • Need to find coefficients a, b, c. • Recall explicit, slope-intercept form : • So:

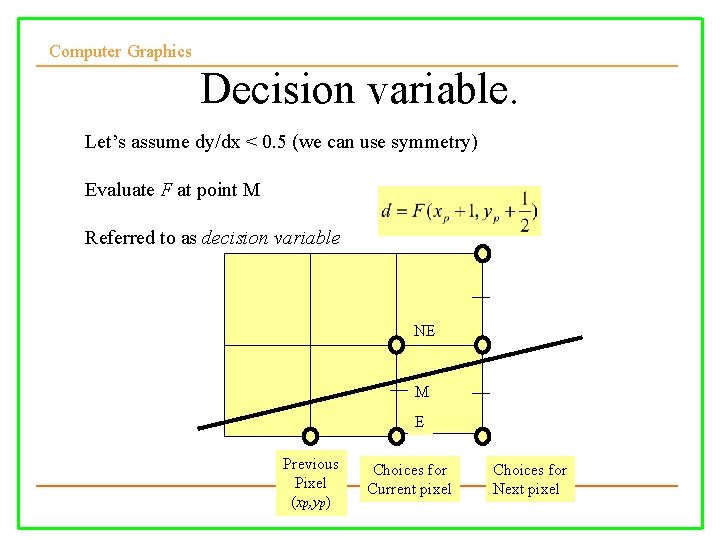
Computer Graphics Decision variable. Let’s assume dy/dx < 0. 5 (we can use symmetry) Evaluate F at point M Referred to as decision variable NE M E Previous Pixel (xp, yp) Choices for Current pixel Choices for Next pixel

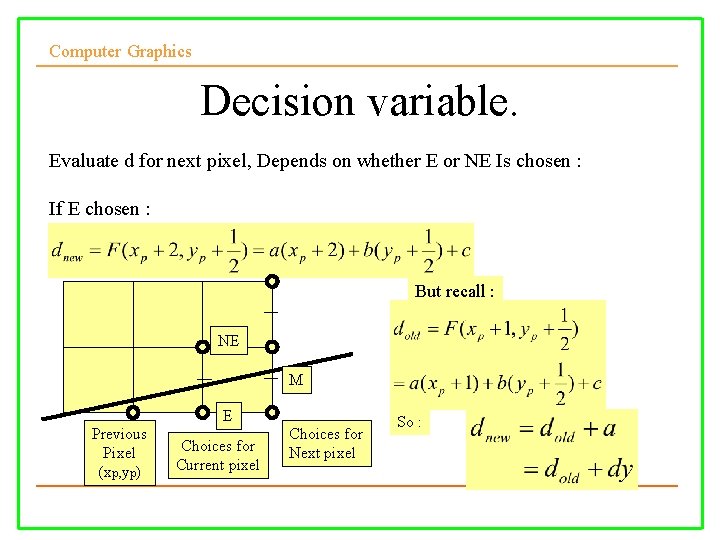
Computer Graphics Decision variable. Evaluate d for next pixel, Depends on whether E or NE Is chosen : If E chosen : But recall : NE M E Previous Pixel (xp, yp) Choices for Current pixel Choices for Next pixel So :

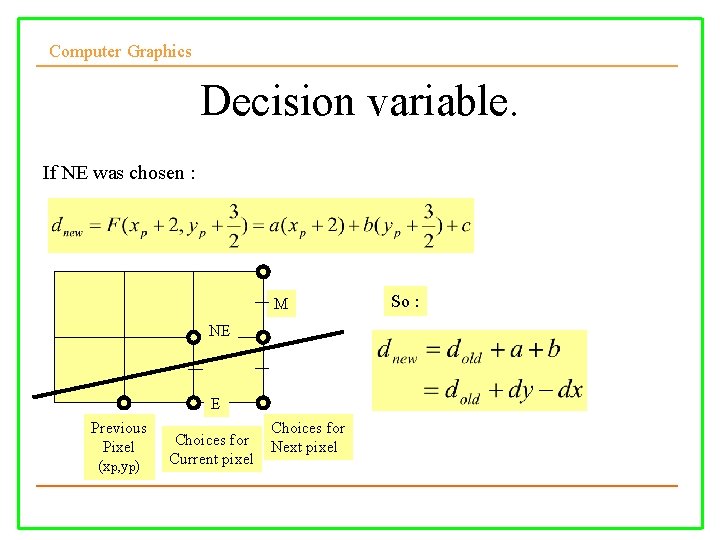
Computer Graphics Decision variable. If NE was chosen : M NE E Previous Pixel (xp, yp) Choices for Current pixel Choices for Next pixel So :

Computer Graphics Summary of mid-point algorithm • Choose between 2 pixels at each step based upon the sign of a decision variable. • Update the decision variable based upon which pixel is chosen. • Start point is simply first endpoint (x 1, y 1). • Need to calculate the initial value for d

Computer Graphics Initial value of d. Start point is (x 1, y 1) But (x 1, y 1) is a point on the line, so F(x 1, y 1) =0 Conventional to multiply by 2 to remove fraction doesn’t effect sign.

Computer Graphics Midpoint algorithm void Midpoint. Line(int x 1, y 1, x 2, y 2) { int dx=x 2 -x 1; int dy=y 2 -y 1; int d=2*dy-dx; int incre. E=2*dy; int incr. NE=2*(dy-dx); x=x 1; y=y 1; Write. Pixel(x, y); while (x < x 2) { if (d<= 0) { d+=incr. E; x++ } else { d+=incr. NE; x++; y++; } Write. Pixel(x, y); } }

Computer Graphics Circle drawing. • Can also use Bresenham to draw circles. • Use 8 -fold symmetry E M SE Previous Pixel Choices for Current pixel Choices for Next pixel

Computer Graphics Circle drawing. • Implicit form for a circle is: • Functions are linear equations in terms of (xp, yp) –Termed point of evaluation

Computer Graphics Summary of line drawing so far. • Explicit form of line – Inefficient, difficult to control. • Parametric form of line. – Express line in terms of parameter t – DDA algorithm • Implicit form of line – Only need to test for ‘side’ of line. – Bresenham algorithm. – Can also draw circles.

Computer Graphics Problems with Bresenham algorithm • Pixels are drawn as a single line unequal line intensity with change in angle. Pixel density = 2. n pixels/mm Can draw lines in darker colours according to line direction. -Better solution : antialiasing ! -(eg. Gupta-Sproull algorithm) Pixel density = n pixels/mm

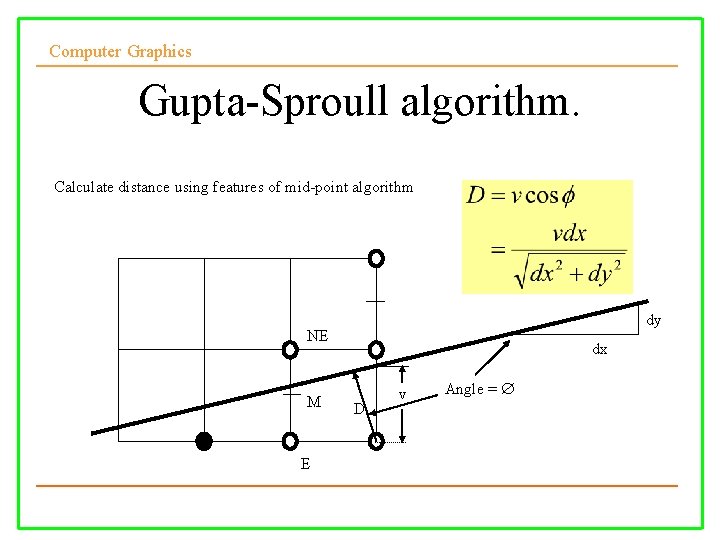
Computer Graphics Gupta-Sproull algorithm. • Calculate the distance of the line and the pixel center • Adjust the colour according to the distance

Computer Graphics Gupta-Sproull algorithm. Calculate distance using features of mid-point algorithm dy NE M E dx D v Angle =

Computer Graphics Gupta-Sproull algorithm (cont) Recall from the midpoint algorithm: Line to draw NE So yp+1 m For pixel E: So: v D yp xp E xp+1 Q

Computer Graphics Gupta-Sproull algorithm (cont) Line to draw From previous slide: NE yp+1 m From the midpoint computation, y xp So: v D p E xp+1 Q

Computer Graphics Gupta-Sproull algorithm (cont) From the midpoint algorithm, we had the decision variable (remember? ) Line to draw Going back to our previous equation: NE yp+1 m v D yp xp E xp+1 Q

Computer Graphics Gupta-Sproull algorithm (cont) So, And the denominator is constant Since we are blurring the line, we also need to compute the distances to points yp – 1 and yp + 1

Gupta-Sproull algorithm (cont) Computer Graphics If the NE pixel had been chosen:

Computer Graphics Gupta-Sproull algorithm (cont) • Compute midpoint line algorithm, with the following alterations: • At each iteration of the algorithm: – If the E pixel is chosen, set numerator = d + dx – If the NE pixel is chosen, set numerator = d – dx – Update d as in the regular algorithm – Compute D = numerator/denominator – Color the current pixel according to D – Compute Dupper = (2 dx-2 vdx)/denominator – Compute Dlower = (2 dx+2 vdx)/denominator – Color upper and lower accordingly