Computer Graphics Lecture 18 3 D TransformationsII Taqdees














































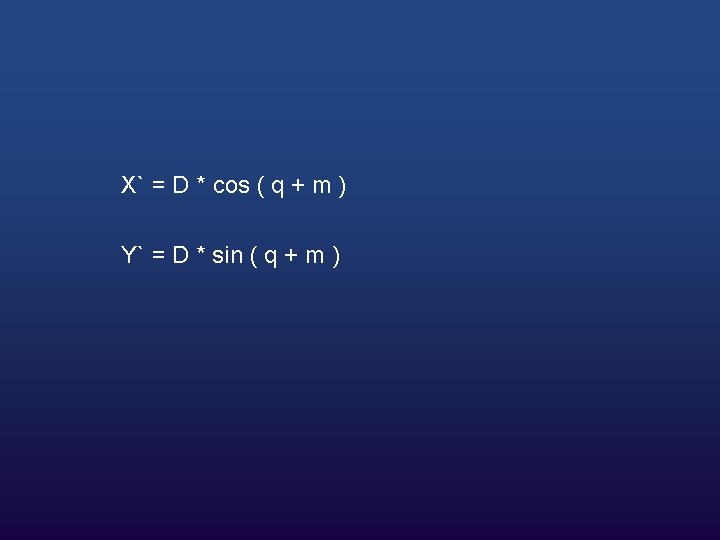

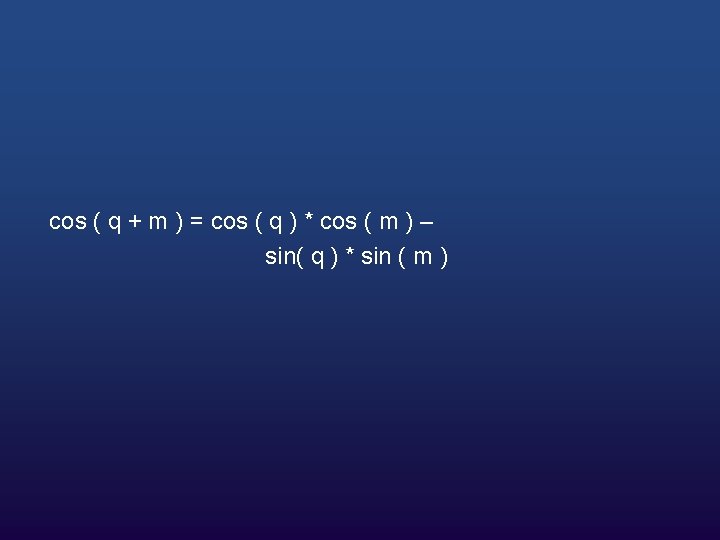


![w X`= [X / cos(q)] * cos (q) * cos(m) – ] *sin(q) * w X`= [X / cos(q)] * cos (q) * cos(m) – ] *sin(q) *](https://slidetodoc.com/presentation_image/5bbf9e9353c68fc8cb3abe8f82c56fd0/image-72.jpg)

![w Y` = D*sin(q+m) = D*[sin(q) * cos(m) + cos(q) * sin(m)] = D*sin(q) w Y` = D*sin(q+m) = D*[sin(q) * cos(m) + cos(q) * sin(m)] = D*sin(q)](https://slidetodoc.com/presentation_image/5bbf9e9353c68fc8cb3abe8f82c56fd0/image-74.jpg)
![w Y` = [ X/ cos(m)] * sin(q ) *cos(m) + [Y/sin(m) ] * w Y` = [ X/ cos(m)] * sin(q ) *cos(m) + [Y/sin(m) ] *](https://slidetodoc.com/presentation_image/5bbf9e9353c68fc8cb3abe8f82c56fd0/image-75.jpg)










- Slides: 85

Computer Graphics Lecture 18 3 -D Transformations-II Taqdees A. Siddiqi cs 602@vu. edu. pk

Rotation is the process of moving a point in space in a non-linear manner

Normalization Note that the process of moving the points so that the POV is at the origin looking down the +Z axis is called normalization.

For Rotation w Rotating a point requires that we know: – 1) the coordinates for the point, and – 2) the rotation angles

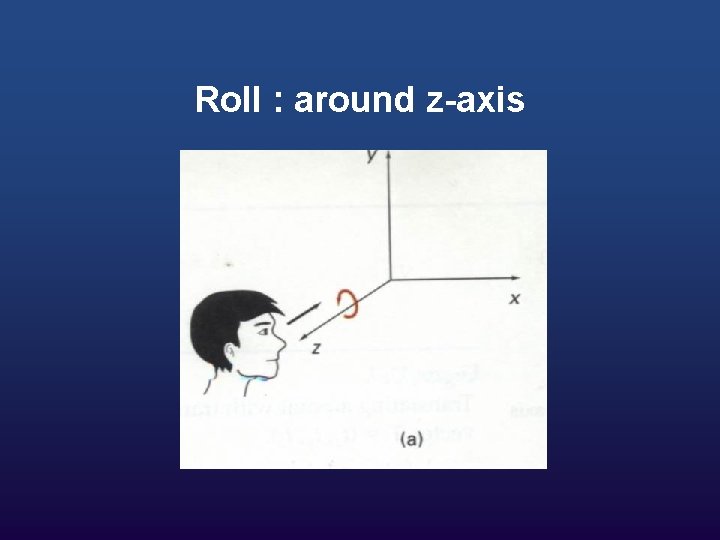
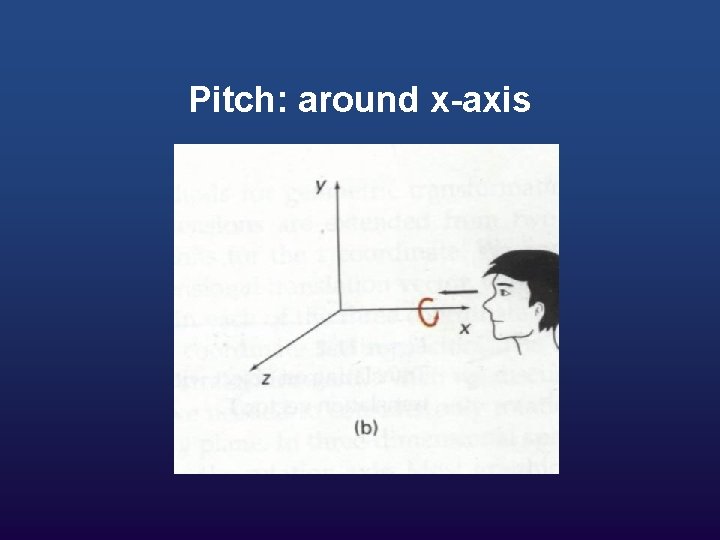
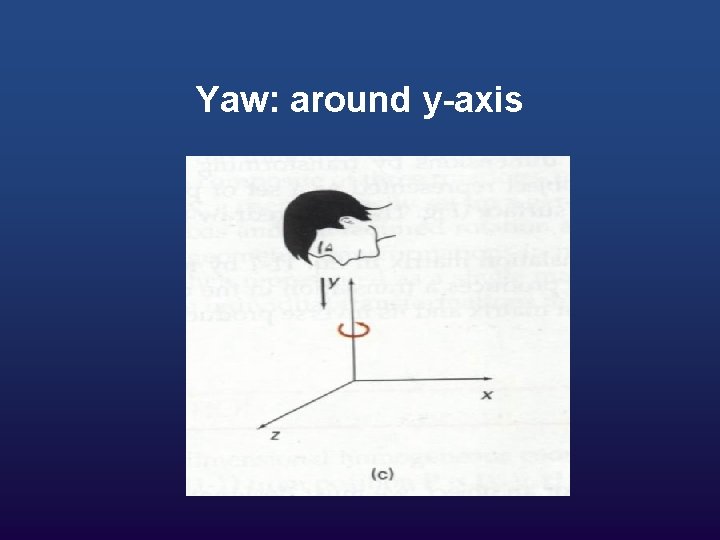
w We need to know three different angles: w How far to rotate around the X axis(YZ rotation, or “pitch”) w How far to rotate around the Y axis (XZ rotation, or “yaw”) w How far to rotate around the Z axis (XY rotation, or “roll”)

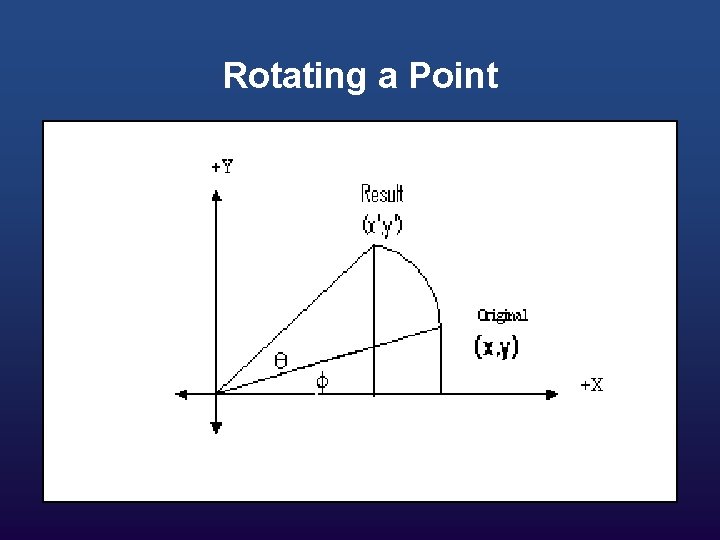
Rotating a Point

w w Repositions an object along a circular path in xy-plane Rotation Angle θ Rotation Point (xr, yr) θ is +ve counterclockwise rotation w θ is -ve clockwise rotation w θ is zero ?

w For simplicity, consider the pivot at origin and rotate point P (x, y) where x = r cos. Ф and y = r sin. Ф w If rotated by θ then: w x′ = r cos(Ф + θ) = r cos. Ф cosθ – r sin. Ф sinθ and w y′ = r sin(Ф + θ) = r cos. Ф sinθ + r sin. Ф cosθ

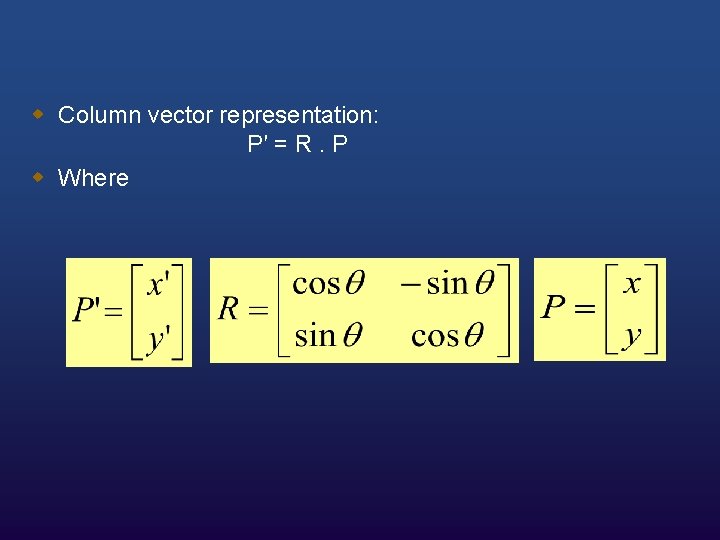
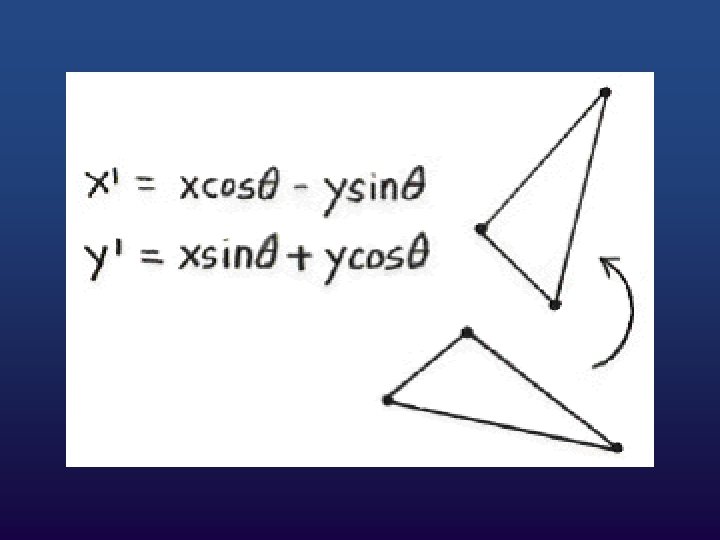
w Replacing r cos. Ф with x and r sin. Ф with y, we have: w x′ = x cosθ – y sinθ and w y′ = x sinθ + y cosθ

w Column vector representation: P′ = R. P w Where

Rotation: Homogeneous Coordinates The rotation can now be expressed using homogeneous coordinates as: Abbreviated as: P’ = R (θ) . P

… Now in 3 D w w Rotation can be about any of the three axes: About z-axis (i. e. in xy plane) About x-axis (i. e. in yz plane) About y-axis (i. e. in xz plane)

Roll : around z-axis

Pitch: around x-axis

Yaw: around y-axis

w Rotation about z-axis (i. e. in xy plane): • x′ = x cosθ – y sinθ • y′ = x sinθ + y cosθ • z’ = z


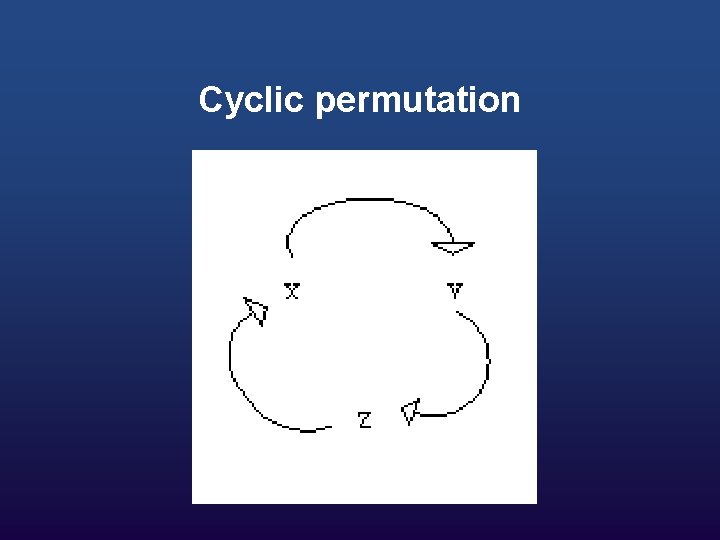
Alright, but what about rotations w. r. t. other axes? Cyclic Permutations of Coordinate Axes

Cyclic permutation

Rotation about x-axis (i. e. in yz plane): x′ = x y′ = y cosθ – z sinθ z′ = y sinθ + z cosθ

Rotation about y-axis (i. e. in xz plane): x′ = z sinθ + x cosθ y ′ = y z′ = z cosθ – x sinθ

Matrix Representations

Rotation about z-axis P` = Rz(θ). P

Rotation about x-axis P` = Rx(θ). P

Rotation about y-axis P` = Ry(θ). P

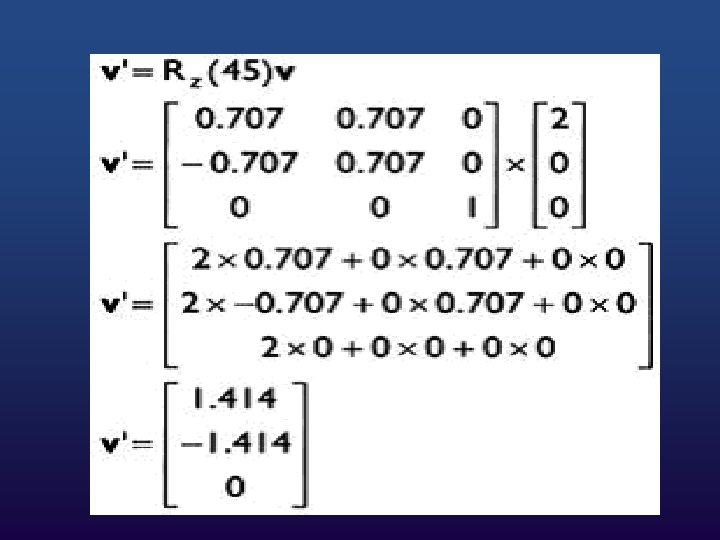
Example w Let's manually rotate the point (2, 0, 0) 45 degrees clockwise about the z axis


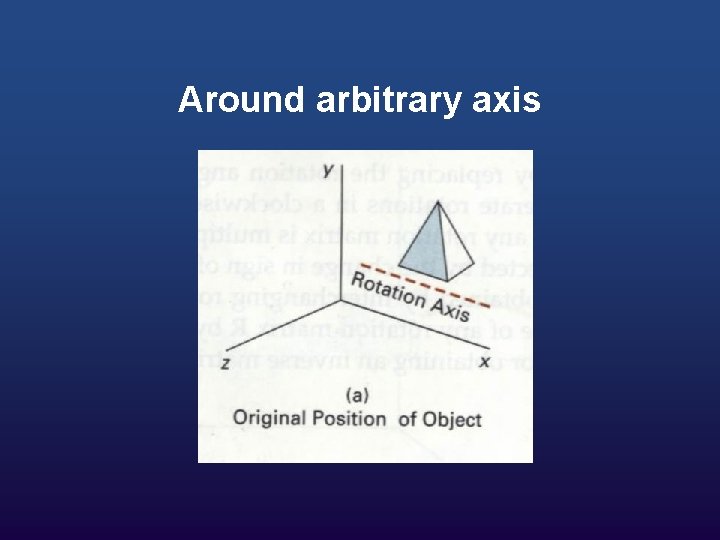
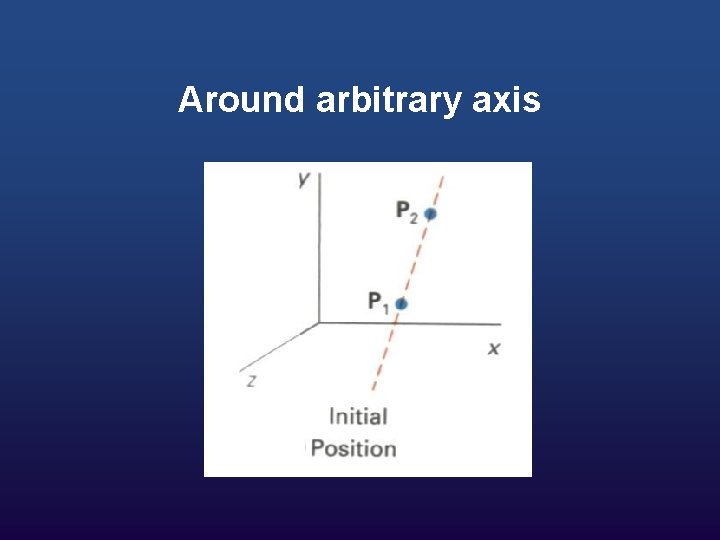
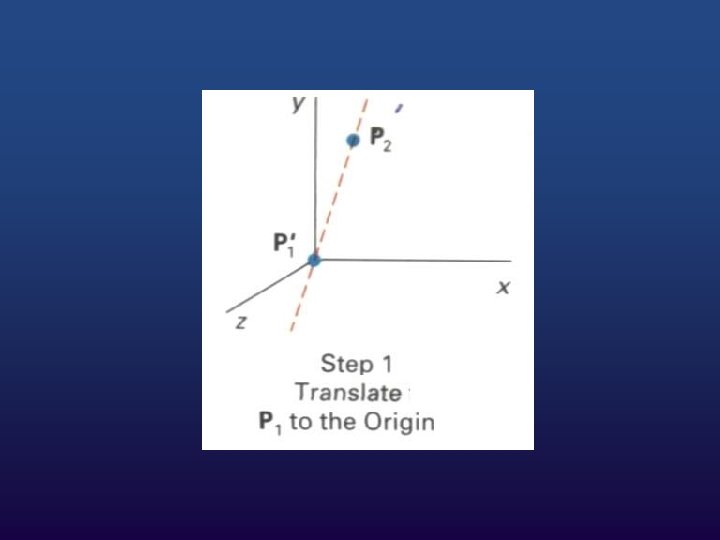
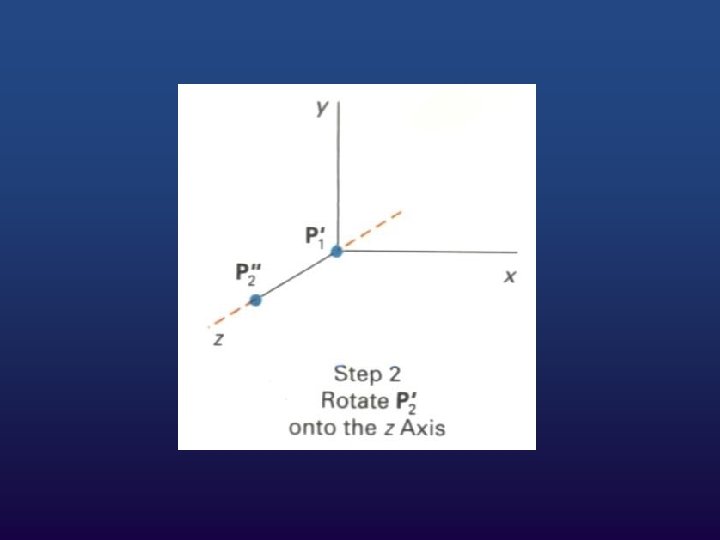
Around arbitrary axis

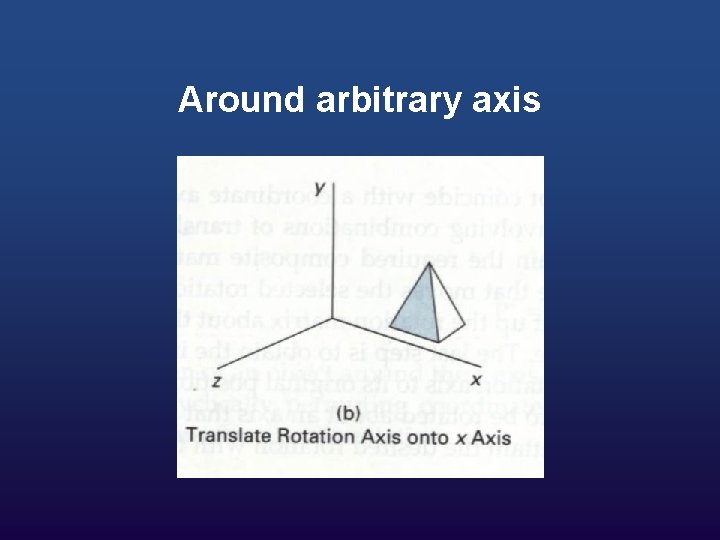
Around arbitrary axis

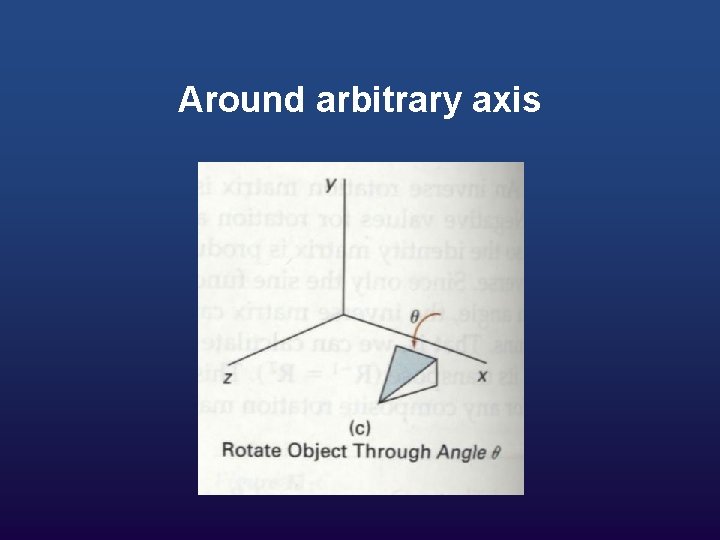
Around arbitrary axis

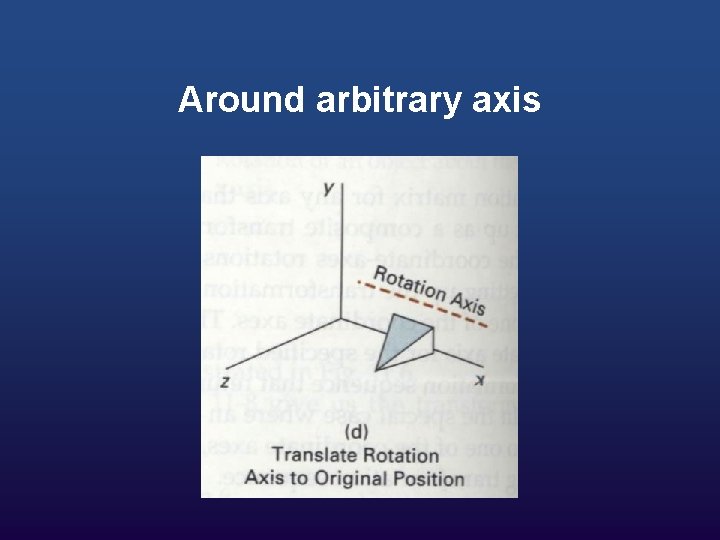
Around arbitrary axis

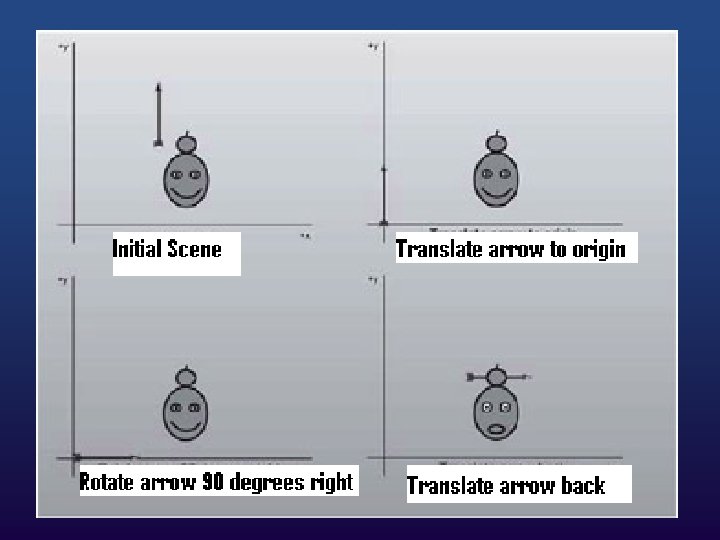
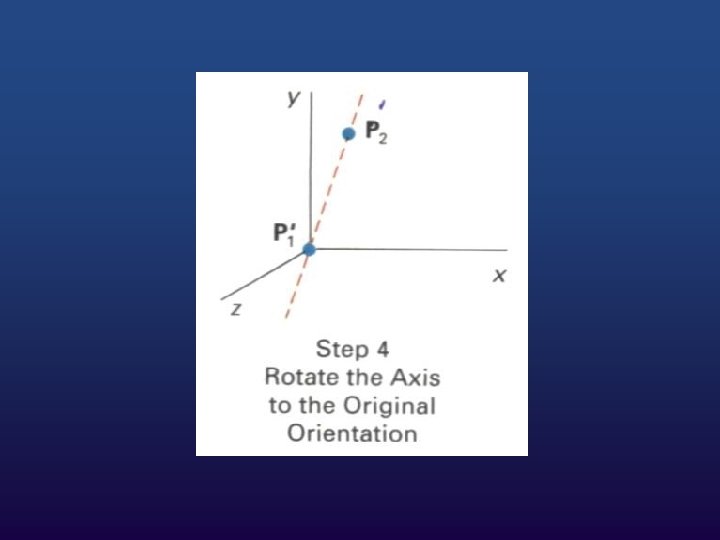
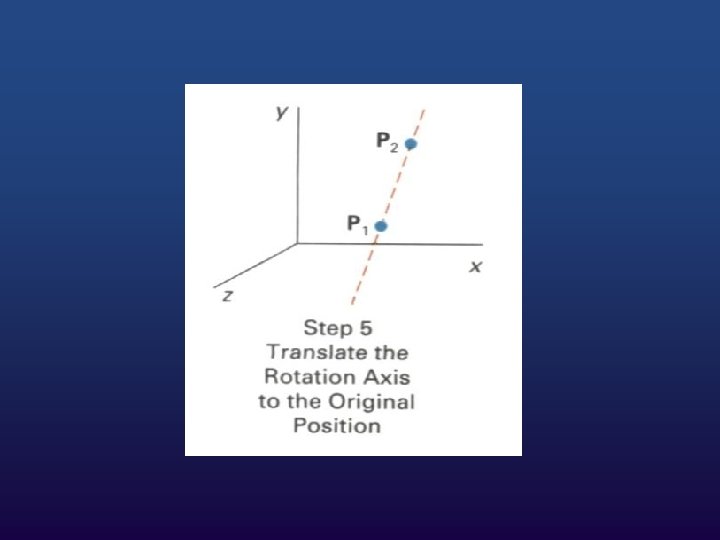
Composite Transformation Now you can take an object and apply a sequence of transformations to it to make it do whatever you want. All you need to do is figure out the sequence of transformations needed and then apply the sequence to each of the points in the model.

As an example, let's say you want to rotate an object sitting at a certain point p around its z axis. You would perform the following sequence of transformations to achieve this



Around arbitrary axis






Scaling

Scaling an object changes its size and repositions the object relative to the coordinate origin. If the transformation parameters are not all equal, relative dimensions in the object are changed

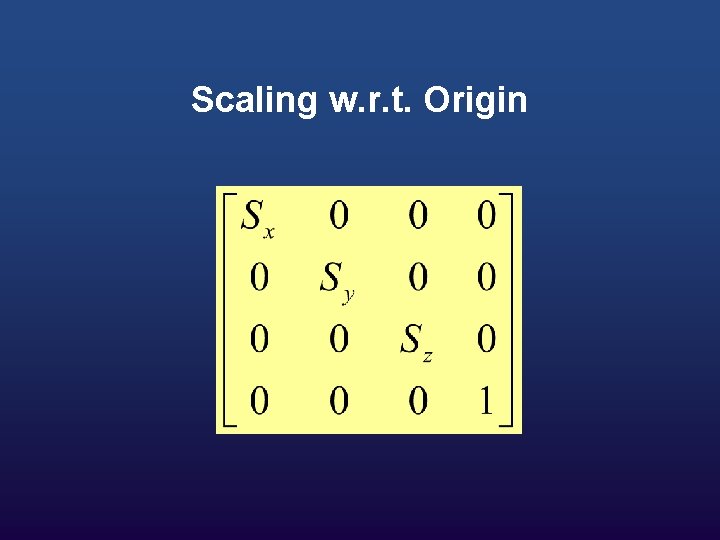
w Coordinate transformations for scaling relative to the origin are w X` = X. Sx w Y` = Y. Sy w Z` = Z. Sz

w 1) Uniform Scaling w 2) Differential Scaling

Uniform Scaling w We preserve the original shape of an object with a uniform scaling w ( Sx = Sy = Sz)

Differential Scaling w We do not preserve the original shape of an object with a differential scaling w ( Sx <> Sy <> Sz)

Scaling w. r. t. Origin

Scaling w. r. t. a fixed position Scaling with respect to a selected fixed position (Xf, Yf, Zf) can be represented with the transformation sequence:

Transformation sequence 1. 2. 3. Translate the fixed point to the origin. Scale the object relative to the coordinate origin Translate the fixed point back to its original position

Composite Transformation

Composite Transformation

Reflection A reflection can be performed relative to a selected reflection axis or with respect to a selected reflection plane.

In general, three-dimensional reflection matrices are set up similarly to those for two dimensions. Reflections relative to a given axis are equivalent to 180 degree rotations.

Reflection of points relative to the X axis

Reflection of points relative to the Y axis

Reflection of points relative to the xy plane

Shears

w Shearing transformations can be used to modify object shapes

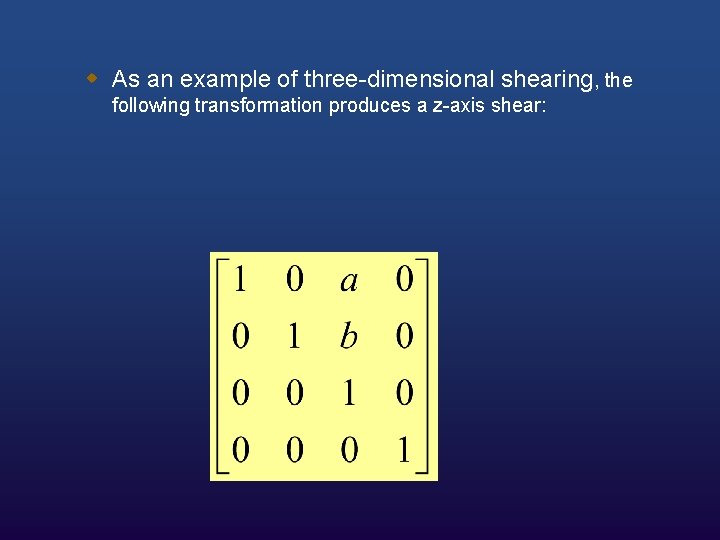
w As an example of three-dimensional shearing, the following transformation produces a z-axis shear:

Y-axis shear

X-axis shear

Computer Graphics Lecture 18

Rotation w. r. t. y-axis: P` = Ry(θ). P

w From the drawing and elementary trigonometry, we can say: cos(q) = X/D or D = X /cos(q) sin(q) = Y/D or D = Y/sin(q)

where D = hypotenuse = length of vector from origin to (x, y) To rotate to our new point, we just add m to q For our new point, we know that: cos ( q + m) = X` / D sin ( q + m) = Y`/ D
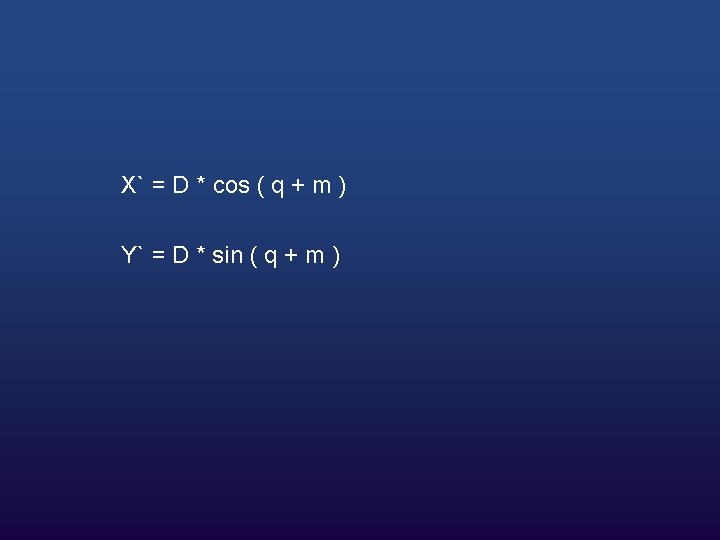

w We can expand these using the addition formulas
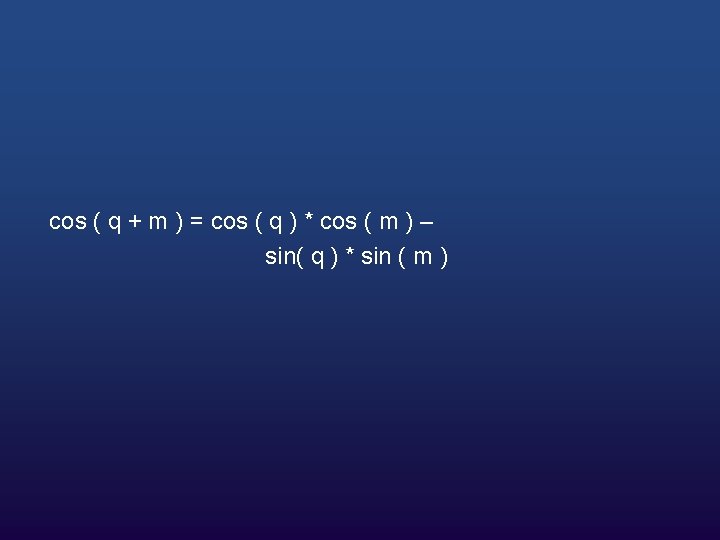
cos ( q + m ) = cos ( q ) * cos ( m ) – sin( q ) * sin ( m )

X` = D * cos (q + m ) =D*[cos ( q ) * cos( m ) – sin ( q ) * sin ( m )] =D*cos ( q ) * cos ( m ) – D*sin ( q )*sin( m )

w w But we noted that D= X / cos(q) D= Y/sin(q) so we can substitute them in :
![w X X cosq cos q cosm sinq w X`= [X / cos(q)] * cos (q) * cos(m) – ] *sin(q) *](https://slidetodoc.com/presentation_image/5bbf9e9353c68fc8cb3abe8f82c56fd0/image-72.jpg)
w X`= [X / cos(q)] * cos (q) * cos(m) – ] *sin(q) * sin(m) w = X * cos(m) – Y*sin(m) [Y/sin(q)

w And we can follow a similar approach to find Y`
![w Y Dsinqm Dsinq cosm cosq sinm Dsinq w Y` = D*sin(q+m) = D*[sin(q) * cos(m) + cos(q) * sin(m)] = D*sin(q)](https://slidetodoc.com/presentation_image/5bbf9e9353c68fc8cb3abe8f82c56fd0/image-74.jpg)
w Y` = D*sin(q+m) = D*[sin(q) * cos(m) + cos(q) * sin(m)] = D*sin(q) * cos(m) + D*cos(q) * sin(m)
![w Y X cosm sinq cosm Ysinm w Y` = [ X/ cos(m)] * sin(q ) *cos(m) + [Y/sin(m) ] *](https://slidetodoc.com/presentation_image/5bbf9e9353c68fc8cb3abe8f82c56fd0/image-75.jpg)
w Y` = [ X/ cos(m)] * sin(q ) *cos(m) + [Y/sin(m) ] * cos(q ) * sin(m) w = X * sin(q) + Y*cos(q)

w So to rotate the point (x, y, z) around the Z axis through an angle of M degrees, we use: w X` = x*cos(M) – y*sin(M) w Y` = x*sin(M) + y*cos(M) w Z` = z

w You see, in the above, we rotate M degrees around the Z axis (“roll”), moving from the +X axis to the +Y axis w But if you look down on the XY plane from the +Z axis, this is a –M degree rotation!

w you can go through a similar process to calculate the rotation formula for rotating around the X axis (“pitch”) and around the Y axis (“yaw”), ending up with:

w w Roll ( rotate around Z axis): x` = x * cos(m ) + y* sin(m) y` = y* cos(m) – x * sin(m) z` = z

w w Pitch ( rotate around the X axis): x` = x y` = y * cos(m) + z * sin(m) z` = z * cos(m) – y*sin(m)

w w Yaw ( rotate about the Y axis): x` = x * cos(m) – z * sin(m) y` = y; z` = x * sin(m) + z * cos(m)

Using Matrices for Rotation

Roll (rotate about the Z axis) | cos(m) | -sin(m) | 0 or P` = Rz(m). P sin(m) cos(m) 0 0 0 | 1 |

Pitch (rotate about the X axis) | 1 | 0 | 0 or 0 cos(m) -sin(m) 0 P` = Rx(m). P 0 sin(m) cos(m) 0 0 | 0 | 1 |

Yaw (rotate about the Y axis) | cos(m) 0 | 0 1 | sin(m) 0 | 0 or P` = Ry(m). P -sin(m) 0 cos(m) 0 0| 0| 0| 0 1|