Computer graphics Scan conversion of Line circle ellipse

Computer graphics Scan conversion of Line , circle & ellipse

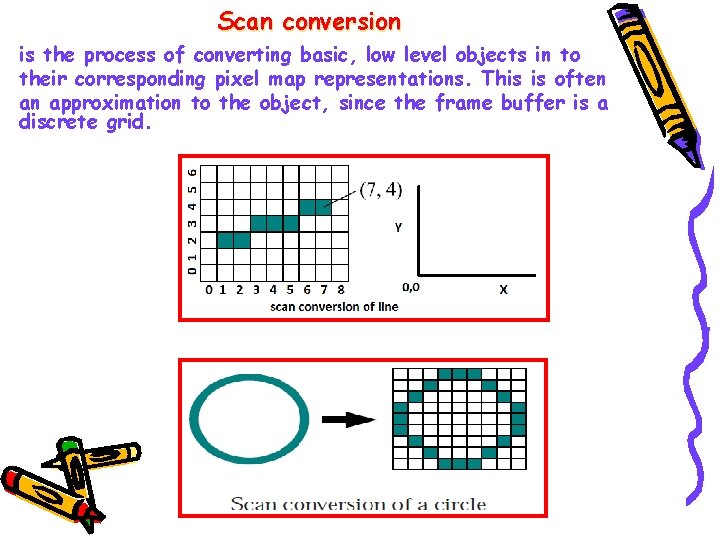
Scan conversion is the process of converting basic, low level objects in to their corresponding pixel map representations. This is often an approximation to the object, since the frame buffer is a discrete grid.

Line Drawing algorithms • Direct or floating or simple algorithm • Digital Differential Analyzer algorithm (DDA) • Bresenham's algorithm or midpoint algorithm • General Bresenham's algorithm Description: • Given the specification for a straight line (parameters). • find the collection of addressable pixels which most closely approximates this line (mathematical equations). • Draw the scan conversion of lines (frame buffer map). Goals • Straight lines should appear straight. • Lines should start and end accurately. • Lines should be drawn as rapidly as possible. • matching endpoints with connecting lines. • Lines should have constant brightness.

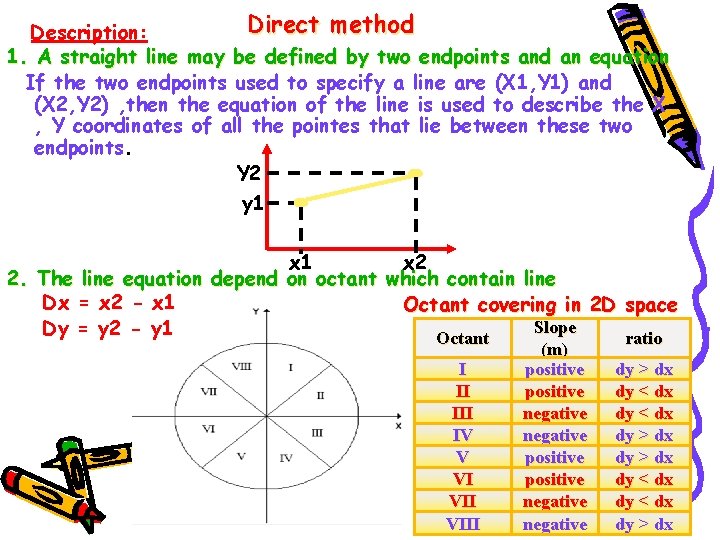
Direct method Description: 1. A straight line may be defined by two endpoints and an equation If the two endpoints used to specify a line are (X 1, Y 1) and (X 2, Y 2) , then the equation of the line is used to describe the X , Y coordinates of all the pointes that lie between these two endpoints. Y 2 y 1 x 2 2. The line equation depend on octant which contain line Dx = x 2 - x 1 Octant covering in 2 D space Slope Dy = y 2 - y 1 Octant ratio I II IV V VI VIII (m) positive negative dy > dx dy < dx dy > dx

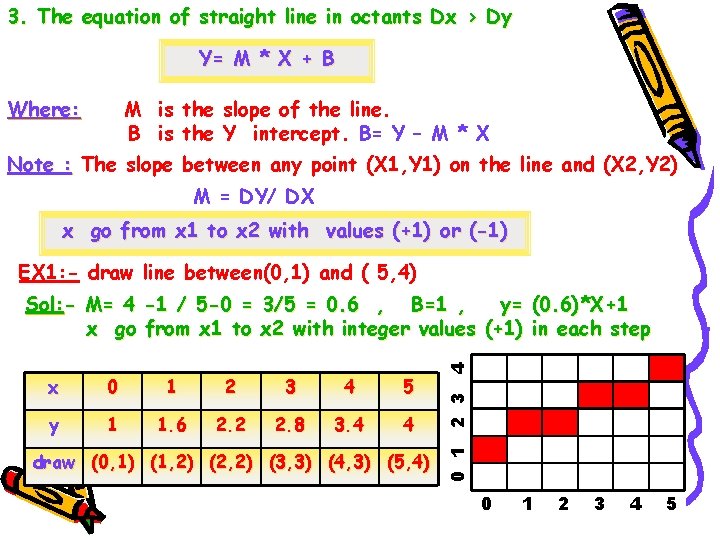
3. The equation of straight line in octants Dx > Dy Y= M * X + B Where: M is the slope of the line. B is the Y intercept. B= Y – M * X Note : The slope between any point (X 1, Y 1) on the line and (X 2, Y 2) M = DY/ DX x go from x 1 to x 2 with values (+1) or (-1) EX 1: - draw line between(0, 1) and ( 5, 4) x 0 1 2 3 4 5 y 1 1. 6 2. 2 2. 8 3. 4 4 draw (0, 1) (1, 2) (2, 2) (3, 3) (4, 3) (5, 4) 0 1 2 3 4 Sol: - M= 4 -1 / 5 -0 = 3/5 = 0. 6 , B=1 , y= (0. 6)*X+1 x go from x 1 to x 2 with integer values (+1) in each step 0 1 2 3 4 5

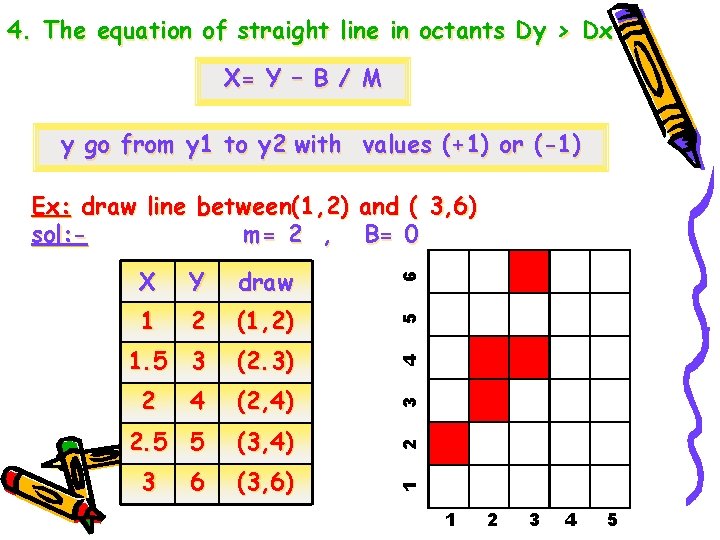
4. The equation of straight line in octants Dy > Dx X= Y – B / M y go from y 1 to y 2 with values (+1) or (-1) 2 (1, 2) 1. 5 3 (2. 3) 4 (2, 4) 2. 5 5 (3, 4) (3, 6) 3 6 3 2 5 1 4 draw 2 Y 1 X 6 Ex: draw line between(1, 2) and ( 3, 6) sol: m= 2 , B= 0 1 2 3 4 5

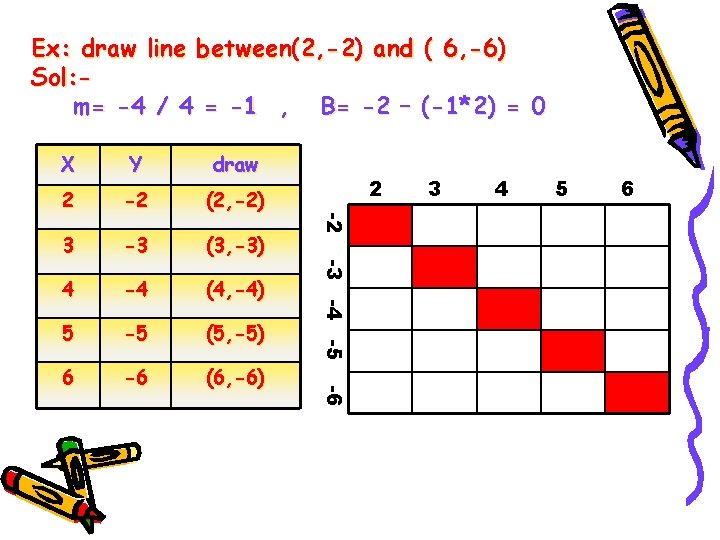
Ex: draw line between(2, -2) and ( 6, -6) Sol: m= -4 / 4 = -1 , B= -2 – (-1*2) = 0 2 -2 (2, -2) 3 -3 (3, -3) 4 -4 (4, -4) 5 -5 (5, -5) 6 -6 (6, -6) 2 -6 draw -3 -4 -5 Y -2 X 3 4 5 6

features: • The algorithm performs a floating-point multiplication for every step in x. This method therefore requires an enormous number of floating-point multiplications, and is therefore expensive. • Round functions are needed • not general for all octants • Can get gaps in the line. example: y = 10. x + 2 x=1, y=12; x=2, y=22.

Algorithm for octant with x 1<x 2 Dim img As New Bitmap(1, 1) img. Set. Pixel(0, 0, Color. Blue) dx = x 2 - x 1 dy = y 2 - y 1 m = dy / dx b = y 1 - m * x 1 For x = x 1 To x 2 e. Graphics. Draw. Image(img, x, Int(y)) y = m * x + b Next HW: develop direct method to draw lines in octants(( Dx >Dy), slope( positive , negative))

Digital Differential Analyzer (DDA) Description: 1. We calculate the length of the line in the X direction ( number of pointes) by the equation Abs(x 2 -x 1) 2. calculate the length of the line in the Y direction ( number of pointes) by the Equation Abs(y 2 -y 1) Where ABS is a function takes the positive of the arguments 3. The Length estimates is equal to the larger of the above two equations. length=max( Abs(y 2 -y 1) , Abs(x 2 -x 1)

4. The increment steps ( d. X and d. Y ) are used to increment the X and Y coordinates for the next pointes to be plotted. Dx= (x 2 -x 1) / length Dy= (y 2 -y 1) / length 5. each point will calculate as equation x = x + Dx y = y + Dy 6. Integer function works as follow( round down) Ex. Integer (8. 5) = 8 Integer (-8. 5) = -9 7. first point we add 0. 5 x = x 1 + 0. 5 y = y 1 + 0. 5

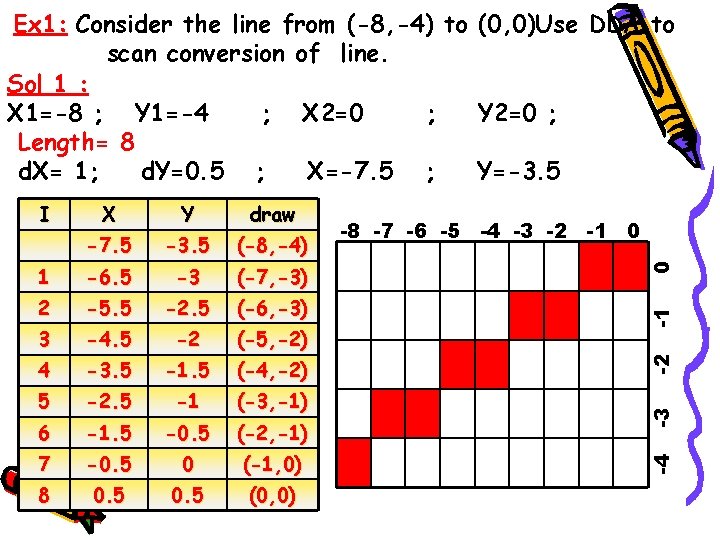
Ex 1: Consider the line from (-8, -4) to (0, 0)Use DDA to scan conversion of line. Sol 1 : X 1=-8 ; Y 1=-4 ; X 2=0 ; Y 2=0 ; Length= 8 d. X= 1; d. Y=0. 5 ; X=-7. 5 ; Y=-3. 5 (-8, -4) 1 -6. 5 -3 (-7, -3) 2 -5. 5 -2. 5 (-6, -3) 3 -4. 5 -2 (-5, -2) 4 -3. 5 -1. 5 (-4, -2) 5 -2. 5 -1 (-3, -1) 6 -1. 5 -0. 5 (-2, -1) 7 -0. 5 0 (-1, 0) 8 0. 5 (0, 0) 0 -7. 5 -8 -7 -6 -5 -4 -3 -2 -1 0 -1 draw -2 Y -3 X -4 I

Algorithm DDA Start Length=ABS (X 2 -X 1) If length < ABS (Y 2 -Y 1) Then Length=ABS (Y 2 -Y 1) d. X = (X 2 - X 1) / Length d. Y = (Y 2 - Y 1) / Length X=X 1 + 0. 5 Y=Y 1 + 0. 5 Plot (Integer (X) , Integer (Y)) For I=1 to Length Begin X=X + d. X Y=Y + d. Y Plot (Integer (X) , Integer (Y)) End Finish

Features of DDA 1 - The algorithm is orientation dependent 2 - The end point accuracy deteriorates 3 - The algorithm suffer from the fact that it must be performed using floating point arithmetic HW 1: Consider the line from (0, 0) to (-8, -4) evaluate the DDA algorithm