COLEGIO NACIONAL DE EDUCACIN PROFESIONAL TCNICA QUINTO SEMESTRE

COLEGIO NACIONAL DE EDUCACIÓN PROFESIONAL TÉCNICA QUINTO SEMESTRE ANÁLISIS DERIVATIVO DE FUNCIONES

CONTENIDO A. Determinación de elementos de funciones. Definición de función y relación. Dominio y rango Gráfica de funciones Raíces Intervalos de crecimiento

FUNCIONES Para poder definir una función, a manera de antecedentes se consideran los siguientes conceptos Conjuntos: Es una asociación de elementos de cualquier tipo y se denota generalmente con las primeras letras del abecedario (mayúsculas)

por ejemplo; A= {1, 3, 5, 7, 9, 11, ……. . } B= {a, b, c, d, ……. . . , x , y , z} N= {x | x pertenece N, donde N es el conjunto de los números naturales}

Producto cartesiano Dados los conjuntos A y B, el producto cartesiano de ellos, denotado por A x B, se define como el conjunto de todos los pares ordenados (a, b) donde a ∈ A y pertenece B, esto es; A x B = {(a, b) |a ∈ A ∧ b ∈ B} Relación: Es cualquier subconjunto del producto cartesiano A x B y se denota generalmente por la letra R.

Considerando tres subconjuntos del producto cartesiano se obtiene las siguientes relaciones

NOTA: ES IMPORTANTE REALIZAR LAS ACTIVIDADES YA QUE ESTO REPRESENTA UNA EVIDENCIA DE APRENDIZAJE PARA LA EVALUACION CONTINUA , PUES AL FINAL DE LA UNIDAD; SERA PARTE DE TU EVALUACION.

DEFINICIÓN DE FUNCIONES Dados los conjuntos de A y B, una función es el conjunto de pares ordenados (a, b), donde a ∈ A, se le denomina dominio de la función y al conjunto formado por las segundas componentes b ∈ B, se le denomina Rango de la función. Note que la definición de una función establece que las primeras componentes de los pares ordenados no se deben repetir, razón por la cual, todas las funciones son relaciones pero no todas las relaciones son funciones, ya que en las relaciones si se puede repetir las primeras componentes

Dados los conjuntos A y B del ejemplo no 1, indique cuales de las relaciones obtenidos R 1, R 2, R 3 son funciones Las relaciones obtenidas del producto cartesiano A x B del ejemplo No 1, fueron las siguientes;

Considerando la definición de función, solamente la relación R 1 es una función en virtud que no se repite ninguno de los primeros elementos En forma complementaria, observe que las relaciones R 2 y R 3 no son funciones en virtud que las primeras componentes se repiten

Actividad Dados los conjuntos A y B, obtenga el producto cartesiano de A y B y tres funciones cualesquiera; A = {-5, 6, -2, 7, 0} y B = {-3, 7, -1, 5}

FUNCION REAL DE VARIABLE REAL Si los conjuntos A y B son subconjuntos de los números reales, entonces se puede establecer una función, que se denomina FUNCIÓN REAL DE LA VARIABLE, que es un conjunto de pares ordenados de números (x, y), en el cual dos pares ordenados distintos no tienen el mismo primer número “x”.

Una función REAL DE VARIABLE REAL, se denota de la siguiente forma F = {(x, y)| y = f (x), con x = ∈ Df y y ∈ R 1} donde y = f(x) es la regla de correspondencia x= y = D = R = es la variable independiente es la variable dependiente es el dominio de la función es el rango de la función

Una función real de variable real, también puede denotarse, en forma simplificada, por alguna de las siguientes maneras F, G, H, o bien f(x), g(x), h(x) o simplemente por “y” La restricción de que dos pares ordenados distintos no pueden tener el mismo primer número x, asegura que y, es único valor especifico de “x”

Encuentre el dominio y el rango de la función F = {(x, y) | y=2 x- 4} En este caso la variable dependiente x no tiene ninguna restricción, es decir puede tomar cualquier valor, esto es x ∈ r , o bien x ∈ (-∞; +∞) De manera similar, al asignar cualquier valor a la variable independiente x, la variable dependiente “y” puede también tomar cualquier valor, es decir y ∈ r , o bien y ∈ (-∞; +∞)

Actividad Encuentre el dominio y rango de la función: G = {(x, y)| y = 3 x + 5}

Encuentre el dominio y el rango de la función F = {(x, y) |y = 1/x-2} En este caso, la variable independiente x no puede tomar el valor de 2, en virtud de que el denominador se hace 0 y la división entre cero no está definida, lo cual se obtiene de la inecuación X -2 ≠ 0 X ≠ 2

De manera similar, de la ecuación; x- 2 = 1/y La variable “y” no puede tomar el valor de cero y ≠ 0 Por lo tanto el dominio de la función es el conjunto de todos los números “x ∈ r con x ≠ 2 donde el conjunto de r es el conjunto de los números reales y el rango de la función es el conjunto de números reales r y ∈ r con y ≠ 0

Obtenga el dominio y el rango de la función con regla de correspondencia En este caso la regla de correspondencia contenga raíces, el dominio se encuentra analizando el radicando es decir 4 – x 2 ≥ - 4

Por lo tanto el dominio de la función es x ∈ [-2; 2] y el rango de la función son todos los números positivos, es decir que y ∈ [0; +∞]

CLASIFICACIÓN DE LA FUNCIÓN Las funciones reales de variable real, en general, se puede clasificar en algebraicas y trascendentes Funciones algebraicas; son aquellas que están formadas por un numero finito de operaciones algebraicas, como son la suma, resta, multiplicación, división, potencia o extracción de raíces. Funciones trascendentes; son aquellas que no pueden considerarse como algebraicas, como son las trigonométricas, logarítmicas, exponenciales, etc. . .

Las funciones también se pueden clasificar de acuerdo a la forma que tiene su regla de correspondencia, así como las funciones pueden ser explicitas e implícitas

Funciones explicitas: son aquellas que en su regla de correspondencia, una variable esta despejada en función de la otra, es decir tiene la forma y = f(x) Funciones implícitas; son aquellas que en su regla de correspondencia, no está despejada ninguna variable en función de la otra, es decir, tiene la forma F (x, y) = 0 En la siguiente tabla aparecen funciones Clasificadas

A algebraica, racional, polinomial, F 1 {(X, Y ) | y = x 2 + 3 x -5} cuadrática y explícita B algebraica, racional, polinomial, y explicita C algebraica, no racional y explicita D algebraica, racional, polinomial, F 4 {(x, y) |x 3 – y +2 = 2 } cubica e implícita E trascendente, explicita F trascendente, trigonométrica y F 6 {(x, y) | 2 sen x – 3 y +1 = 0 } explicita G trascendente, mayor entero y F 7 {(x, y) | y = [ x ]} explicita exponencial no F 2 {(x, y) | y = x 2 – x +1/x+2} si x≠ 2 y

Actividad Clasifique las siguientes funciones

GRAFICA DE UNA FUNCIÓN Si F es una función, entonces la gráfica de F es el conjunto de todos los puntos (x, y) localizado en un sistema de coordenadas bidimensional, para los cuales (x, y) es un par ordenado de la función F. Para trazar la gráfica de una función, es común el uso de la regla de correspondencia y = f(x), la cual denota el valor particular de la variable “y”, que le corresponde al valor de la variable “x” La definición de una función establece que a cada valor de x, en el dominio de la función, le corresponde un único valor de “y” y lo cual implica que gráficamente ninguna recta vertical puede intersectar a la gráfica de una función en más de un punto.

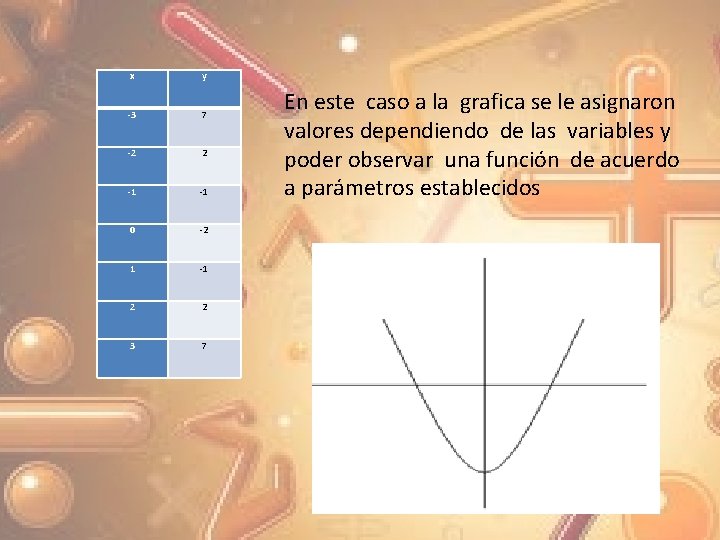
1. - Grafique la siguiente función y determine su dominio y rango F = {x, y) | y = x 2 -2} Para trazar la gráfica de esta función se construye una tabulación asignándole un número suficiente y representativo de valores a la variable independiente “x” los cuales dependen del intervalo de variación de dominio de la función y con base en la regla de correspondencia y = f(x) se obtiene los valores correspondientes de la variable dependiente “y”, de la siguiente manera, para obtener la gráfica que se muestra

x y -3 7 -2 2 -1 -1 0 -2 1 -1 2 2 3 7 En este caso a la grafica se le asignaron valores dependiendo de las variables y poder observar una función de acuerdo a parámetros establecidos

Actividad Grafique la siguiente función G = {(x, y)| y = x 2 +1}

DETERMINE SU DOMINIO Y RANGO

x -5 -4 -3 3 4 5 y 4 7 0 0 7 4 Donde el dominio y rango X ∈ (- ∞; 3] ∪ [3; +∞) y y ∈ [0; +∞)

OPERACIONES CON FUNCIONES Se consideran ahora las operaciones básicas con funciones reales de variables real, que son, la adición sustracción, multiplicación y división, las cuales se definen de la siguiente manera Para las funciones reales de variables reales F= {(x, y) | y = f(x)} y G = {(x, y) | y = g(x)}

Con dominios Df y Dg respectivamente, a) F +G = { (x, y) |y = f(x) + g(x) } entonces las funciones F + G, F – G FG y F/G, son funciones con dominio b) F - G = { (x, y) |y = f(x) – g(x) } Df ∩ Dg, definidas por d) F/G = {(x, y) | y = f(x)/g(x), donde g(x) ≠ 0 } c) F G = {(x, y) | y = f(x) g(x) }

Para dar la interpretación simples a estas operaciones en el siguiente ejemplo se consideran ejemplo de pares ordenados finitos Obtenga F +G, F – G, FG F/G para las siguientes funciones F ={(-1, 3), (0, 5), (1, 7), (2, -3), (3, -1)} y G = {(0, -2), (-1, 6), (2, -4), (3, 0)} En este caso Df {-1, 0, 1, 2, 3} y Dg = {0, -1, 2, 3} y la intersección de ambos dominios es Df ∩ Dg = (0, 2, 3) Por lo tanto F+G = {(0, 5+ (-3)), (2, -3)+ (-4), (3 -1+0)} Eso es F+G = {(0, 3), (2, -7), (3, 1)

De manera similar F-G = {(0, 7), (2, 1), (3, -1)} F G = { (0, -10), (2, 12), (3, 0)} F/G = {(0, - 2/5), (2, 3/4)} Note que en este caso g(3)= 0, no se considera el resultado ya que la división entre cero no está definida

ACTIVIDAD Obtenga F+ G, F-G, FG y F/G para las siguientes funciones F= {(-2, -4), (-1, 5), (0, -1), (1, -7), (, 10)} y G = {(-2, -2), (-1, -6), (3, -3), (5, 1)}

COMPOSICIÓN DE FUNCIONES Otra operación que se realiza con las funciones y que por su importancia es conveniente estudiar por separado, es la composición de funciones, la cual se define de la siguiente manera Para las funciones de reales de variable real F = {(x, y) | y = f(x) y G = {x, y) | y= g(x)} Con dominio Df y Dg, respectivamente, la composición de F con G, denotada por F*G, es la función F*G = {(x, y) | y = f (g(x))} Donde el dominio de la función composición F*G es el conjunto de todos los números x en donde el dominio de G, tales que g(x) está en el dominio de F

LA INVERSA DE UNA FUNCION El concepto de inversa de una función presupone que el dominio y el rango se invierten, razón por la cual no toda función tiene inversa, ya que al invertir el dominio por el rango puede ser que las primeras componentes se repitan y por lo tanto deje de ser función Para que una función tenga inversa, es necesario que sea inyectiva, es decir, que no se repitan los elementos ni el dominio ni el rango

Una función es inyectiva si f(x) = f(x 2) solo si x 1 = x 2 Gráficamente una función inyectiva se caracteriza porque toda recta horizontal intersecta a la gráfica de la función en solamente un punto Con estos antecedentes se puede ahora definir a la función a la inversa de la siguiente manera