Chng 4 KHNG GIAN VECTOR Th S L

Chương 4 – KHÔNG GIAN VECTOR Th. S. LÊ HOÀNG TUẤN

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON Xét tập hợp n lần định nghĩa Cụ thể,

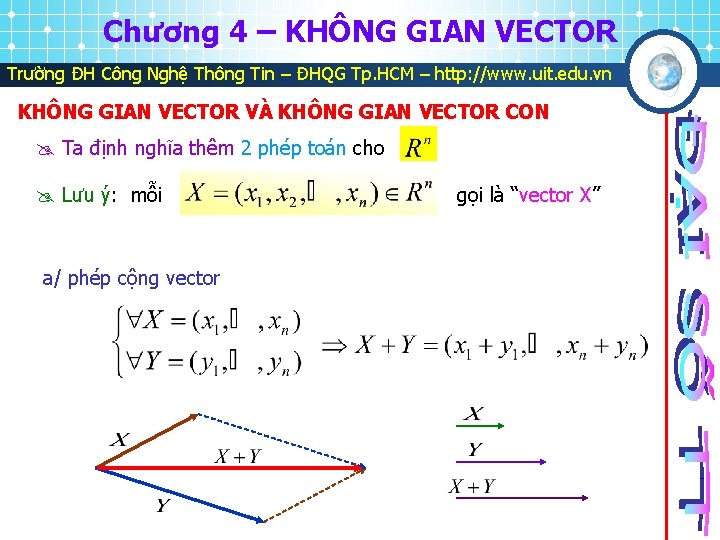
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON Ta định nghĩa thêm 2 phép toán cho Lưu ý: mỗi a/ phép cộng vector gọi là “vector X”

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON b/ phép nhân số thực với vector Lưu ý c. X cùng phương với X, nhưng có thể đổi chiều và độ dài Cấu trúc đại số gọi là không gian vector ( KGVT ) trên R

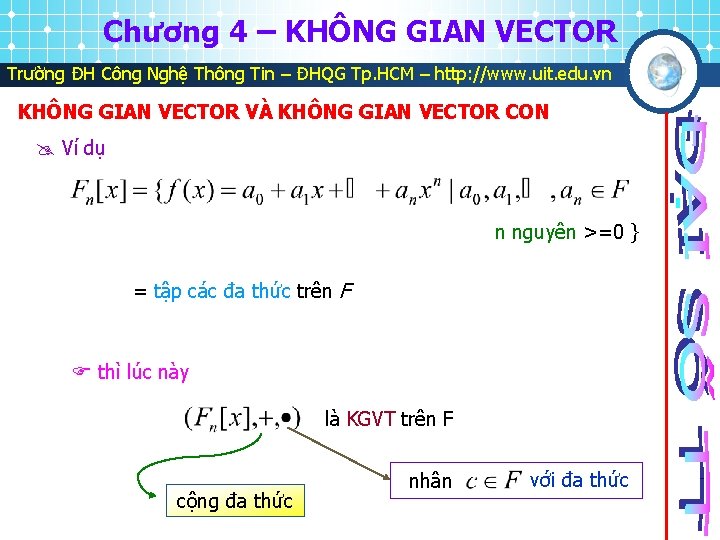
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON Ví dụ n nguyên >=0 } = tập các đa thức trên F thì lúc này là KGVT trên F cộng đa thức nhân với đa thức

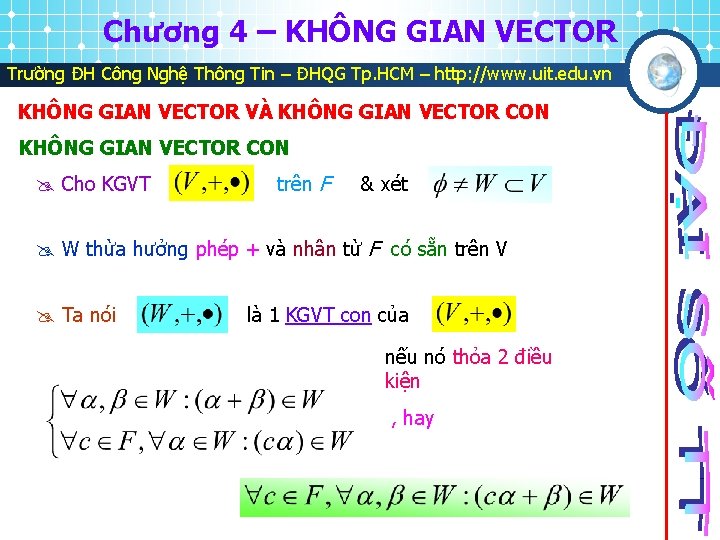
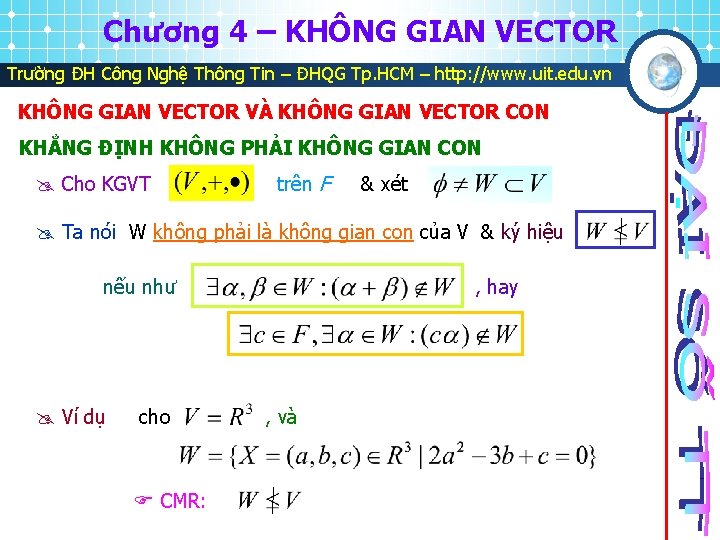
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON Cho KGVT trên F & xét W thừa hưởng phép + và nhân từ F có sẵn trên V Ta nói là 1 KGVT con của nếu nó thỏa 2 điều kiện , hay

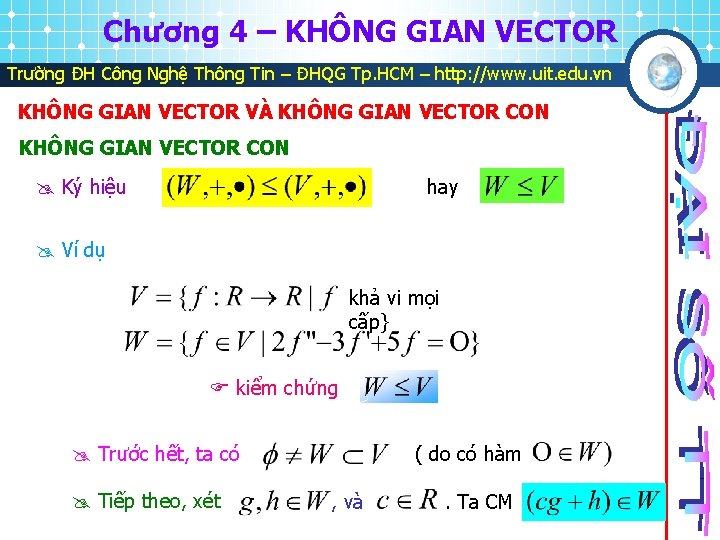
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON Ký hiệu hay Ví dụ khả vi mọi cấp} kiểm chứng Trước hết, ta có Tiếp theo, xét ( do có hàm , và . Ta CM

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON Thật vậy, do KL: , nên

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON KHẲNG ĐỊNH KHÔNG PHẢI KHÔNG GIAN CON Cho KGVT trên F & xét Ta nói W không phải là không gian con của V & ký hiệu nếu như Ví dụ cho CMR: , hay , và

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON KHẲNG ĐỊNH KHÔNG PHẢI KHÔNG GIAN CON Cách 1: (dùng phép +) do do mà vì KL: Cách 2: (dùng phép *) mà vì

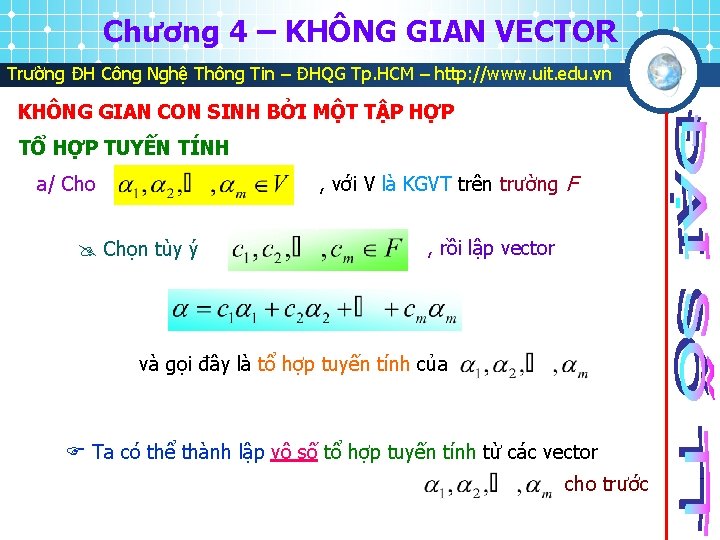
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN CON SINH BỞI MỘT TẬP HỢP TỔ HỢP TUYẾN TÍNH , với V là KGVT trên trường F a/ Cho Chọn tùy ý , rồi lập vector và gọi đây là tổ hợp tuyến tính của Ta có thể thành lập vô số tổ hợp tuyến tính từ các vector cho trước

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON TỔ HỢP TUYẾN TÍNH b/ Nếu ( với , thì ta nói là 1 THTT có từ S Ví dụ trong , cho giả sử ta chọn thì lập được

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON TỔ HỢP TUYẾN TÍNH Ví dụ (tt) Còn nếu chọn , thì ta lập

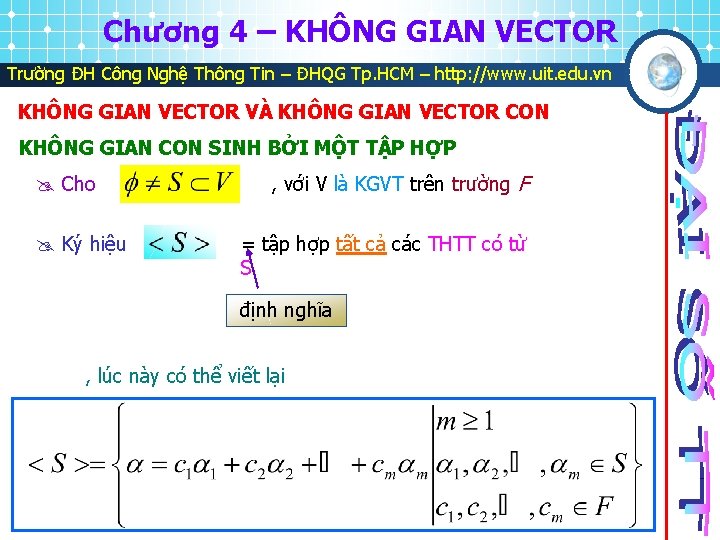
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON KHÔNG GIAN CON SINH BỞI MỘT TẬP HỢP Cho Ký hiệu , với V là KGVT trên trường F = tập hợp tất cả các THTT có từ S định nghĩa , lúc này có thể viết lại

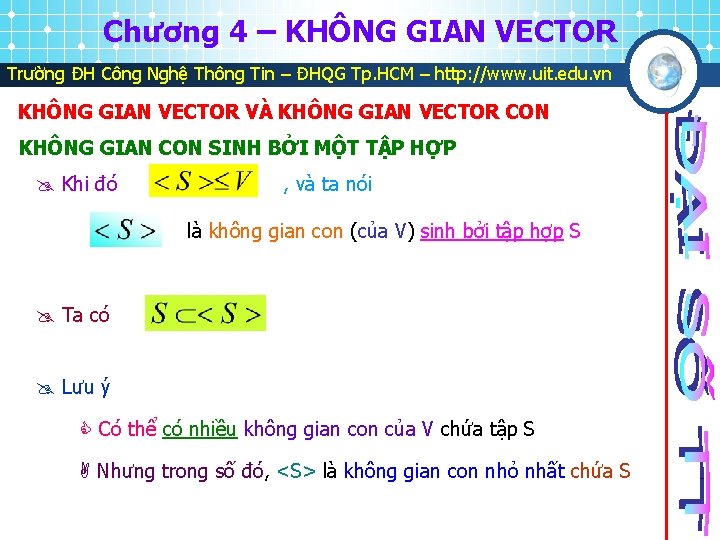
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON KHÔNG GIAN CON SINH BỞI MỘT TẬP HỢP Khi đó , và ta nói là không gian con (của V) sinh bởi tập hợp S Ta có Lưu ý Có thể có nhiều không gian con của V chứa tập S Nhưng trong số đó, <S> là không gian con nhỏ nhất chứa S

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn KHÔNG GIAN VECTOR VÀ KHÔNG GIAN VECTOR CON KHÔNG GIAN CON SINH BỞI MỘT TẬP HỢP Lưu ý nếu ( có đúng m vector ) thì = tập hợp tất cả các THTT có từ S TÍNH ĐỘC LẬP TUYẾN TÍNH & PHỤ THUỘC TUYẾN TÍNH Cho , tiếp theo ta xét hệ PTTT ( ẩn số )

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÍNH ĐỘC LẬP TUYẾN TÍNH & PHỤ THUỘC TUYẾN TÍNH Hệ này có ( ít nhất ) 1 nghiệm là a/ Nếu hệ có nghiệm duy nhất (chính là nghiệm tầm thường này) thì ta nói S độc lập tuyến tính (đltt) , nghĩa là không có vector nào trong S được tính theo các vector còn lại trong S b/ Nếu hệ có nhiều nghiệm không tầm thường (có vô số nghiệm) thì ta nói S phụ thuộc tuyến tính (pttt) , nghĩa là có vector nào đó của S được tính theo các vector còn lại trong S

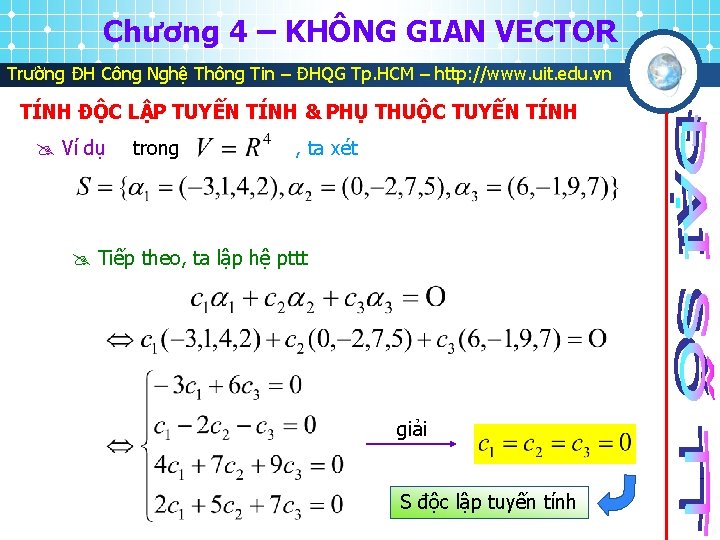
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÍNH ĐỘC LẬP TUYẾN TÍNH & PHỤ THUỘC TUYẾN TÍNH Ví dụ trong , ta xét Tiếp theo, ta lập hệ pttt giải S độc lập tuyến tính

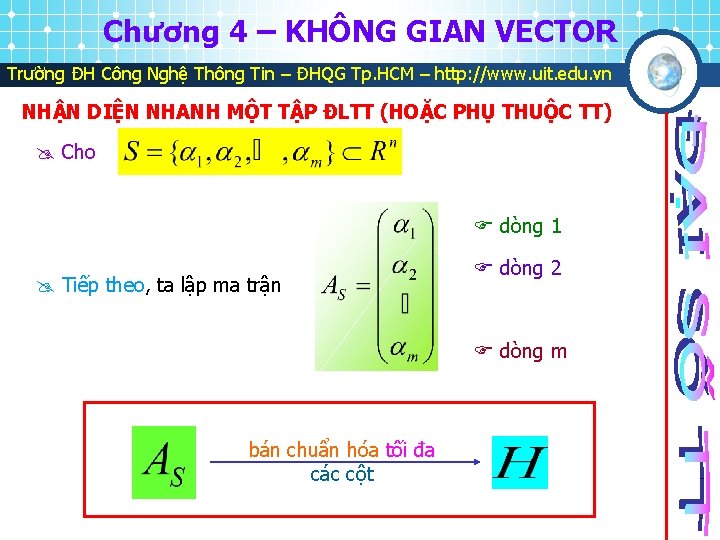
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN NHANH MỘT TẬP ĐLTT (HOẶC PHỤ THUỘC TT) Cho dòng 1 Tiếp theo, ta lập ma trận dòng 2 dòng m bán chuẩn hóa tối đa các cột

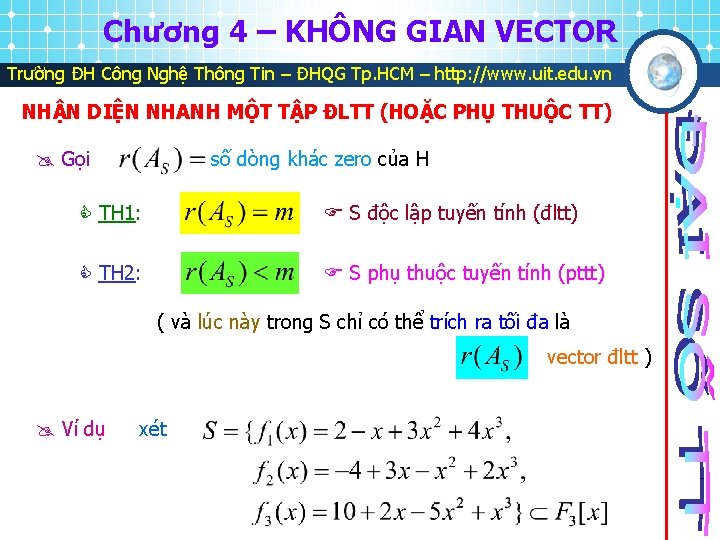
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN NHANH MỘT TẬP ĐLTT (HOẶC PHỤ THUỘC TT) Gọi số dòng khác zero của H TH 1: S độc lập tuyến tính (đltt) TH 2: S phụ thuộc tuyến tính (pttt) ( và lúc này trong S chỉ có thể trích ra tối đa là vector đltt ) Ví dụ xét

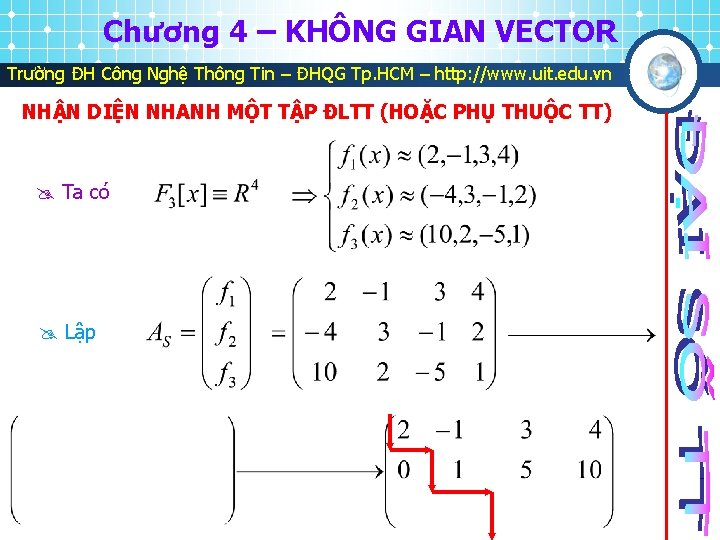
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN NHANH MỘT TẬP ĐLTT (HOẶC PHỤ THUỘC TT) Ta có Lập

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN NHANH MỘT TẬP ĐLTT (HOẶC PHỤ THUỘC TT) Ta có ( do H có 3 dòng khác zero ) S độc lập tuyến tính Ví dụ 2 Lập xét ( vì

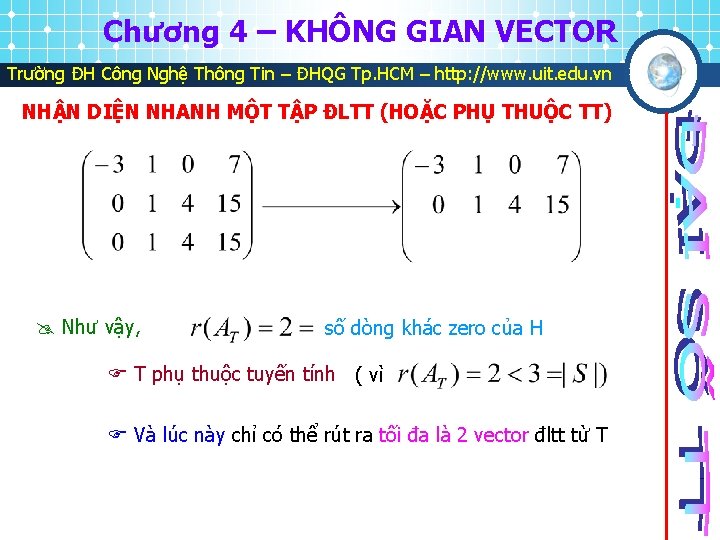
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN NHANH MỘT TẬP ĐLTT (HOẶC PHỤ THUỘC TT) Như vậy, số dòng khác zero của H T phụ thuộc tuyến tính ( vì Và lúc này chỉ có thể rút ra tối đa là 2 vector đltt từ T

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn CƠ SỞ CỦA KHÔNG GIAN VECTOR Vấn đề cho KGVT V sinh bởi tập S Ta muốn tìm mà Nếu tìm được S’ thì S là tập sinh chưa tối tiểu Nếu không tìm được S’ thì S là tập sinh tối tiểu Lưu ý xét KGVT Nếu S đltt thì S là tập sinh tối tiểu Nếu S pttt thì S là tập sinh chưa tối tiểu

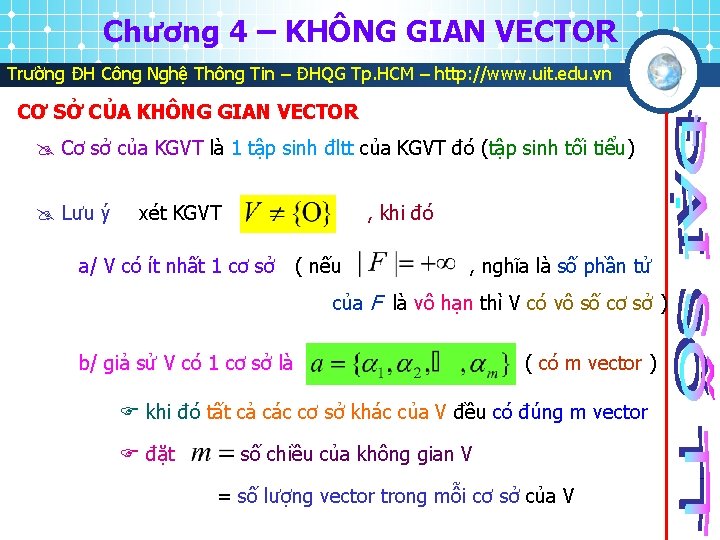
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn CƠ SỞ CỦA KHÔNG GIAN VECTOR Cơ sở của KGVT là 1 tập sinh đltt của KGVT đó (tập sinh tối tiểu) Lưu ý xét KGVT , khi đó a/ V có ít nhất 1 cơ sở ( nếu , nghĩa là số phần tử của F là vô hạn thì V có vô số cơ sở ) b/ giả sử V có 1 cơ sở là ( có m vector ) khi đó tất cả các cơ sở khác của V đều có đúng m vector đặt số chiều của không gian V = số lượng vector trong mỗi cơ sở của V

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn CƠ SỞ CỦA KHÔNG GIAN VECTOR ( dimension of V ) Ký hiệu c/ giả sử V có 1 cơ sở a ( gồm vô số vector ) , khi đó các cơ sở khác của V có vô số vector Ta ghi Ví dụ vì ( V là không gian vô hạn chiều ) có 1 cơ sở thông dụng là đltt và

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn CƠ SỞ CỦA KHÔNG GIAN VECTOR Hay Ta nói là cơ sở chính tắc của vậy Ví dụ 2 tương tự có cơ sở chính tắc là và

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN NHANH 1 CƠ SỞ TRONG Fn a/ nếu , nghĩa là thì , ta có b/ nếu , ứng với , và sao cho thì c/ nếu là 1 cơ sở cho và có tọa độ không tỷ lệ là 1 cơ sở của , và ta xét ( có n vector ) trong

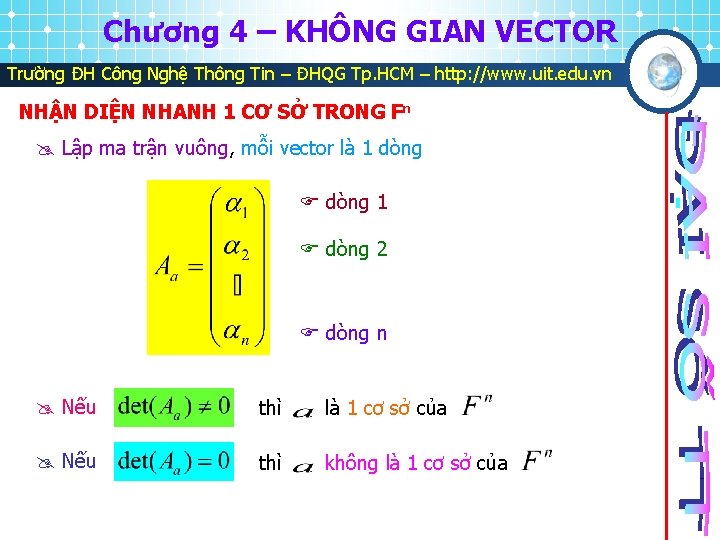
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN NHANH 1 CƠ SỞ TRONG Fn Lập ma trận vuông, mỗi vector là 1 dòng 1 dòng 2 dòng n Nếu thì là 1 cơ sở của Nếu thì không là 1 cơ sở của

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN NHANH 1 CƠ SỞ TRONG Fn Ví dụ trong Lập cho

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN NHANH 1 CƠ SỞ TRONG Fn Ví dụ (tt) KL: là 1 cơ sở của không là cơ sở của

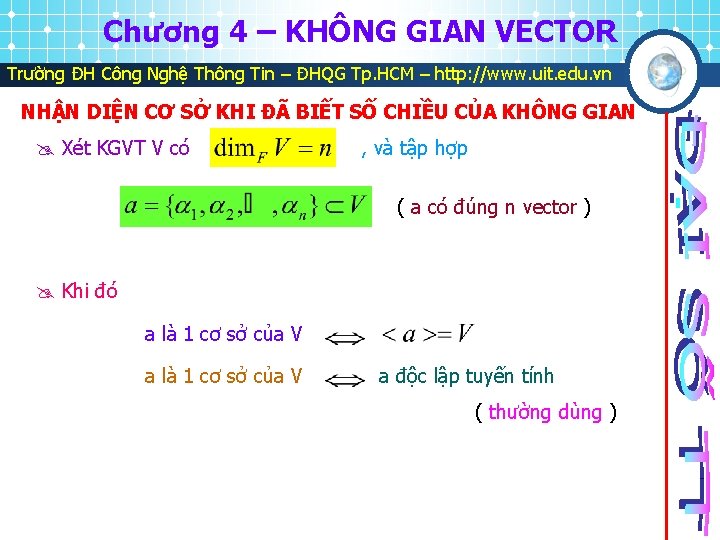
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn NHẬN DIỆN CƠ SỞ KHI ĐÃ BIẾT SỐ CHIỀU CỦA KHÔNG GIAN Xét KGVT V có , và tập hợp ( a có đúng n vector ) Khi đó a là 1 cơ sở của V a độc lập tuyến tính ( thường dùng )

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM TẬP SINH CỦA KHÔNG GIAN PHỤ THUỘC THAM SỐ Ví dụ cho CM Ta có và chỉ ra 1 tập sinh S cho W

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM TẬP SINH CỦA KHÔNG GIAN PHỤ THUỘC THAM SỐ , với , trong đó

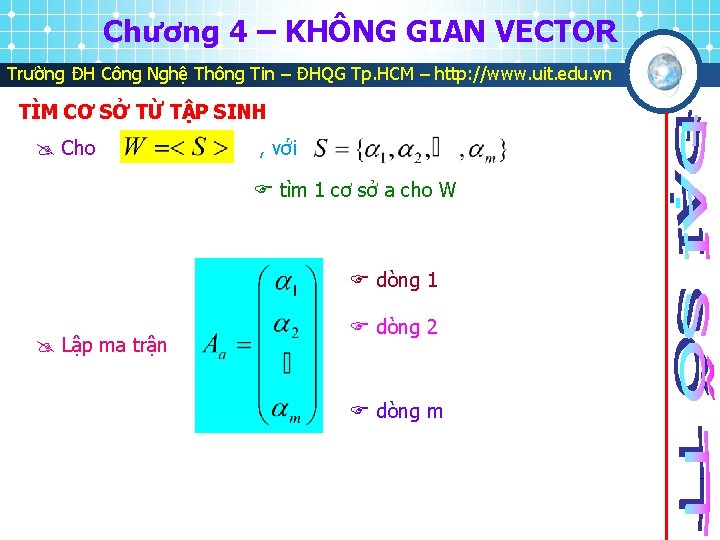
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ TỪ TẬP SINH Cho , với tìm 1 cơ sở a cho W dòng 1 Lập ma trận dòng 2 dòng m

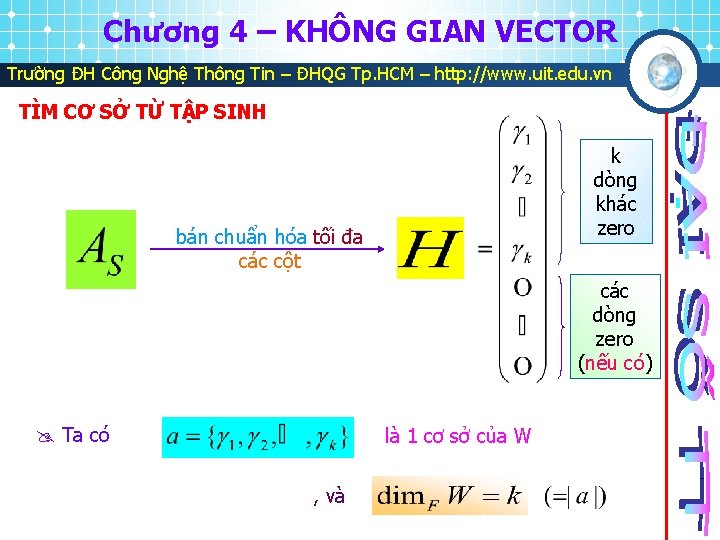
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ TỪ TẬP SINH k dòng khác zero bán chuẩn hóa tối đa các cột các dòng zero (nếu có) Ta có là 1 cơ sở của W , và

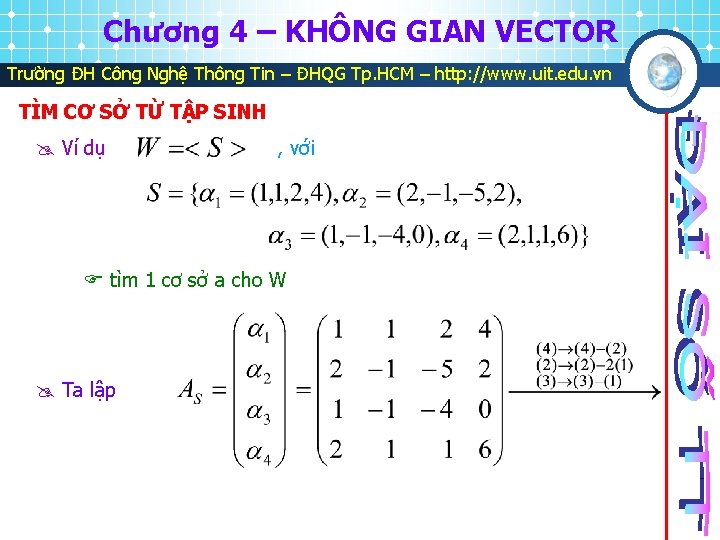
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ TỪ TẬP SINH Ví dụ , với tìm 1 cơ sở a cho W Ta lập

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ TỪ TẬP SINH W có cơ sở là , và

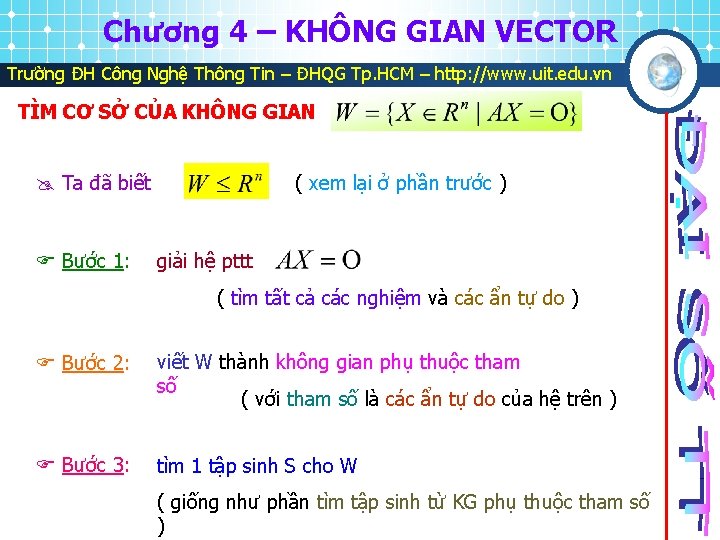
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ CỦA KHÔNG GIAN Ta đã biết Bước 1: ( xem lại ở phần trước ) giải hệ pttt ( tìm tất cả các nghiệm và các ẩn tự do ) Bước 2: viết W thành không gian phụ thuộc tham số ( với tham số là các ẩn tự do của hệ trên ) Bước 3: tìm 1 tập sinh S cho W ( giống như phần tìm tập sinh từ KG phụ thuộc tham số )

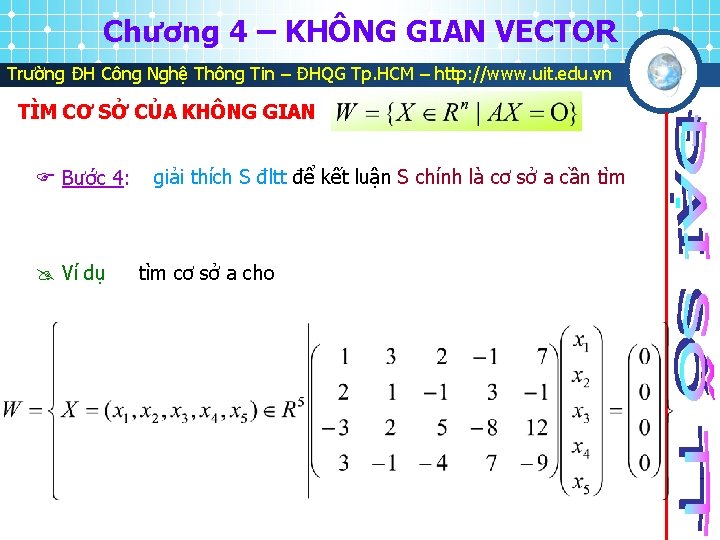
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ CỦA KHÔNG GIAN Bước 4: Ví dụ giải thích S đltt để kết luận S chính là cơ sở a cần tìm cơ sở a cho

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ CỦA KHÔNG GIAN Trước hết, ta giải hệ

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ CỦA KHÔNG GIAN Nghiệm Vậy ( không gian phụ thuộc tham số )

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ CỦA KHÔNG GIAN Vậy , với Ta có S độc lập tuyến tính giải ( nghĩa là hệ Vậy W có cơ sở là , và

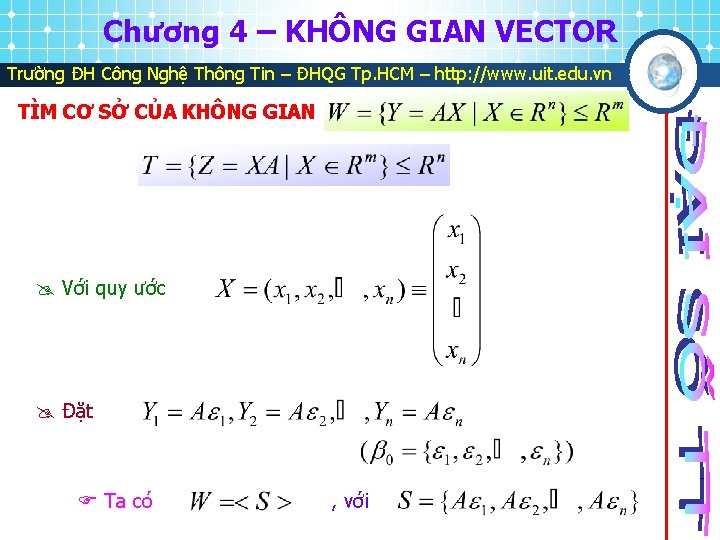
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ CỦA KHÔNG GIAN Với quy ước Đặt Ta có , với

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ CỦA KHÔNG GIAN Giải thích do , với rồi từ tập sinh S, ta tìm được cơ sở a cho W

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TÌM CƠ SỞ CỦA KHÔNG GIAN Tương tự, ta đặt Ta có Ví dụ , với

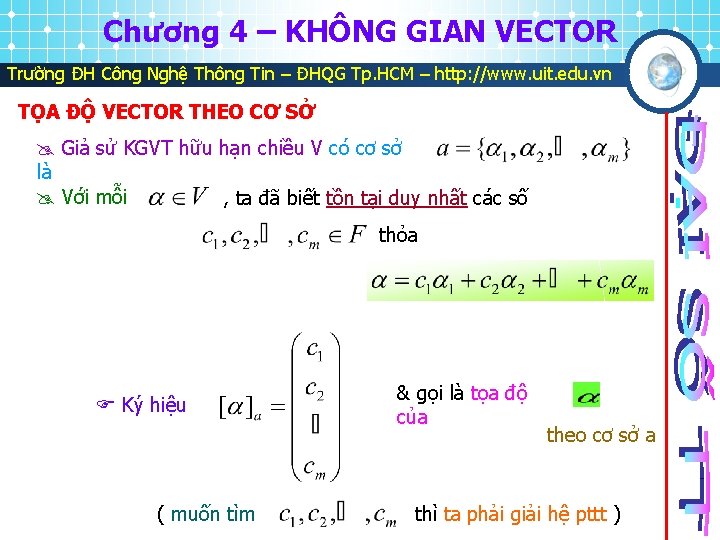
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TỌA ĐỘ VECTOR THEO CƠ SỞ Giả sử KGVT hữu hạn chiều V có cơ sở là Với mỗi , ta đã biết tồn tại duy nhất các số thỏa Ký hiệu ( muốn tìm & gọi là tọa độ của theo cơ sở a thì ta phải giải hệ pttt )

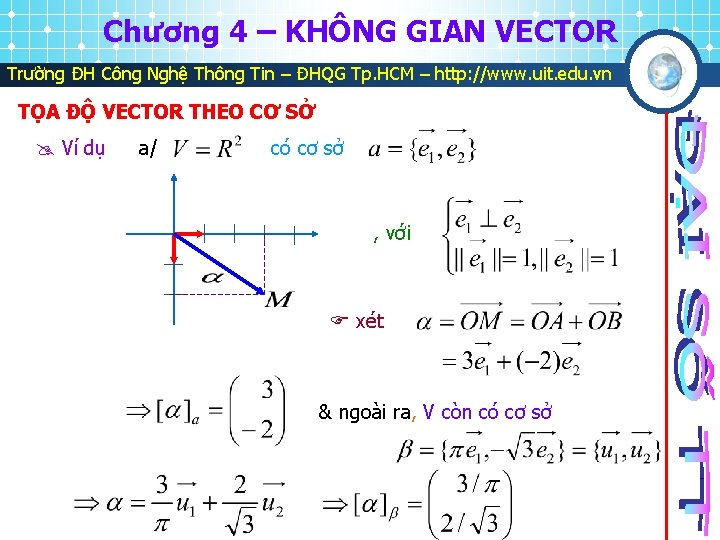
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TỌA ĐỘ VECTOR THEO CƠ SỞ Ví dụ a/ có cơ sở , với xét & ngoài ra, V còn có cơ sở

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TỌA ĐỘ VECTOR THEO CƠ SỞ Ngoài ra, V còn có cơ sở khác là có cơ sở b/ xét thỏa hỏi

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TỌA ĐỘ VECTOR THEO CƠ SỞ Ta có Cho Đặt hỏi

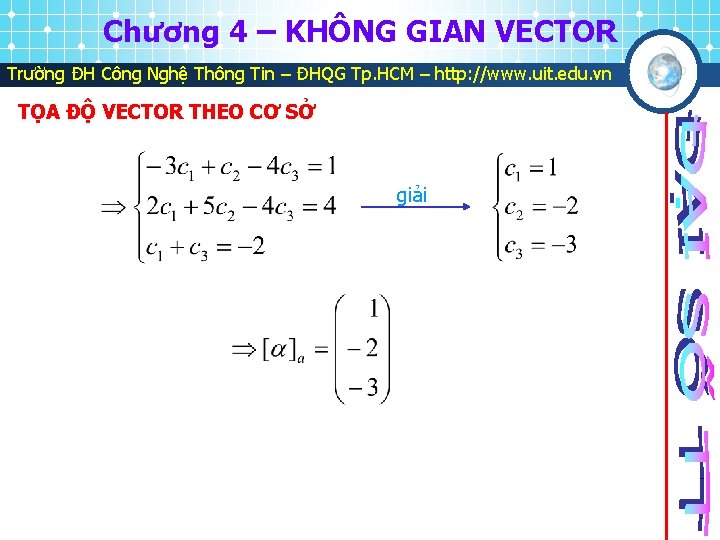
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn TỌA ĐỘ VECTOR THEO CƠ SỞ giải

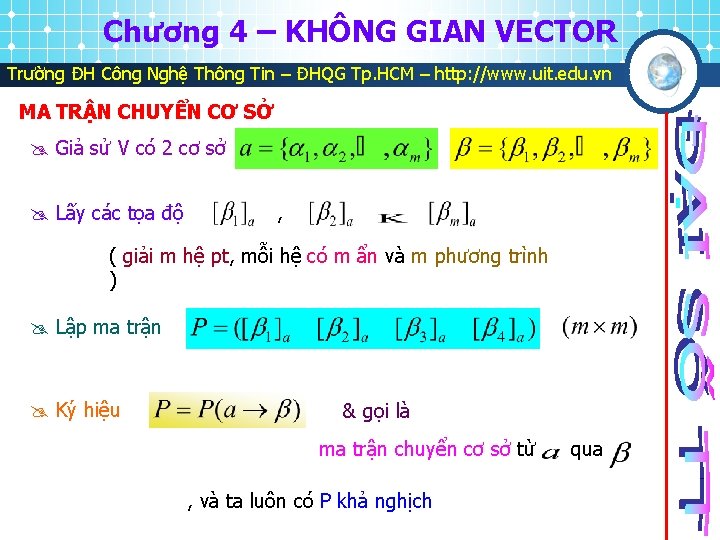
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn MA TRẬN CHUYỂN CƠ SỞ Giả sử V có 2 cơ sở Lấy các tọa độ , ( giải m hệ pt, mỗi hệ có m ẩn và m phương trình ) Lập ma trận Ký hiệu & gọi là ma trận chuyển cơ sở từ , và ta luôn có P khả nghịch qua

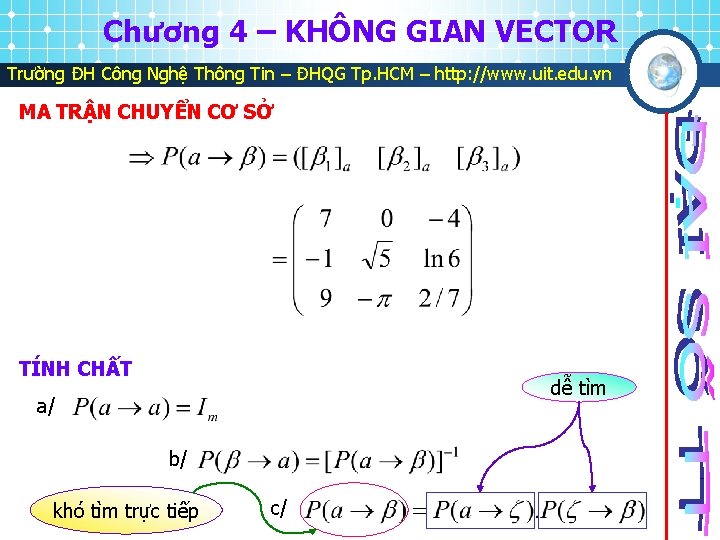
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn MA TRẬN CHUYỂN CƠ SỞ Ví dụ biết rằng V có 2 cơ sở là , và , đồng thời

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn MA TRẬN CHUYỂN CƠ SỞ TÍNH CHẤT dễ tìm a/ b/ khó tìm trực tiếp c/

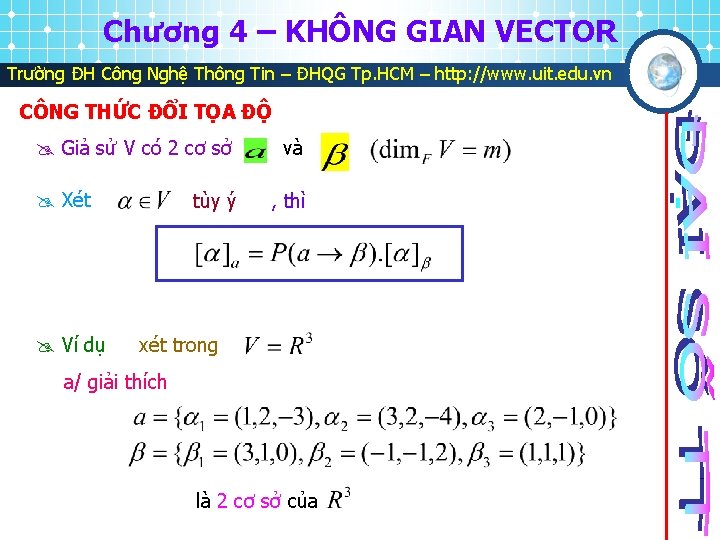
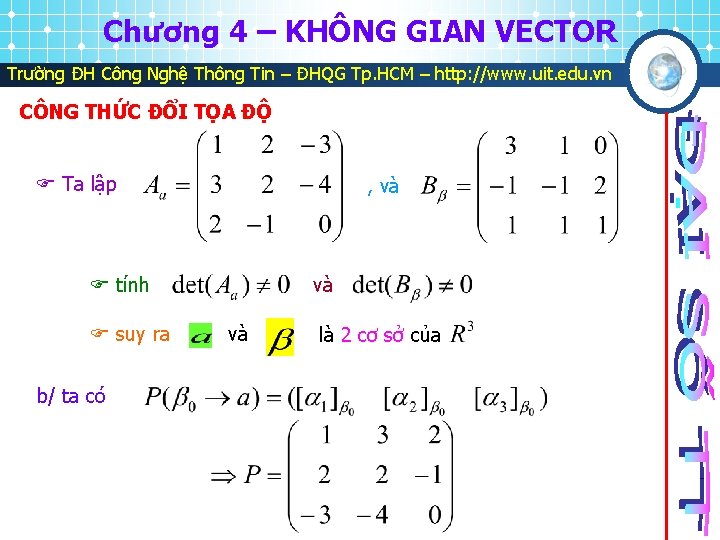
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn CÔNG THỨC ĐỔI TỌA ĐỘ Giả sử V có 2 cơ sở Xét Ví dụ tùy ý và , thì xét trong a/ giải thích là 2 cơ sở của

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn CÔNG THỨC ĐỔI TỌA ĐỘ Ta lập , và tính suy ra b/ ta có và và là 2 cơ sở của

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn CÔNG THỨC ĐỔI TỌA ĐỘ Tương tự Tiếp theo xét Ta có và có tính

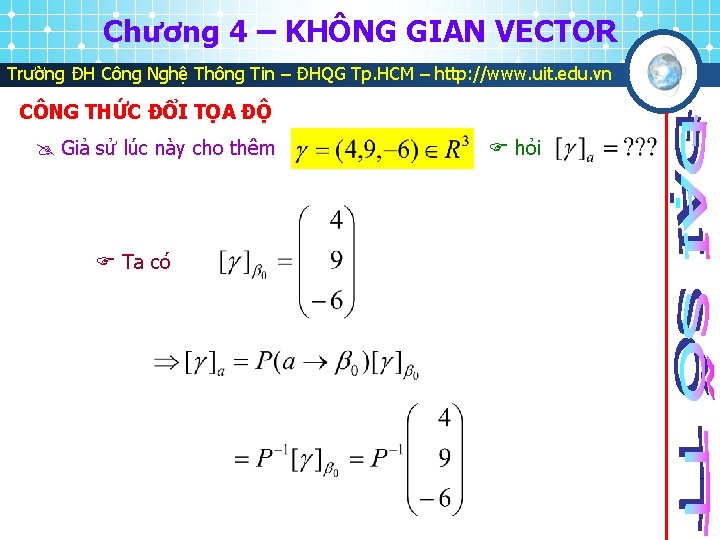
Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn CÔNG THỨC ĐỔI TỌA ĐỘ Giả sử lúc này cho thêm Ta có hỏi

Chương 4 – KHÔNG GIAN VECTOR Trường ĐH Công Nghệ Thông Tin – ĐHQG Tp. HCM – http: //www. uit. edu. vn CÔNG THỨC ĐỔI TỌA ĐỘ Xét Ta có , có tìm