GEOMETRIA EN LESPAI PUNTS RECTES I PLANS A

GEOMETRIA EN L’ESPAI PUNTS, RECTES I PLANS A L’ESPAI

OPERACIONS AMB VECTORS • Suma de vectors: • Producte d’un vector per un escalar: • Producte vectorial

VECTORS: NOTACIÓ MATRICIAL • Tres vectors de l’espai formen base de l’espai si i només si són linealment independents, és a dir, si no són coplanaris. • Per comprovar que tres vectors són linealment independents és suficient comprovar que el determinant de les seves components és diferent de zero:

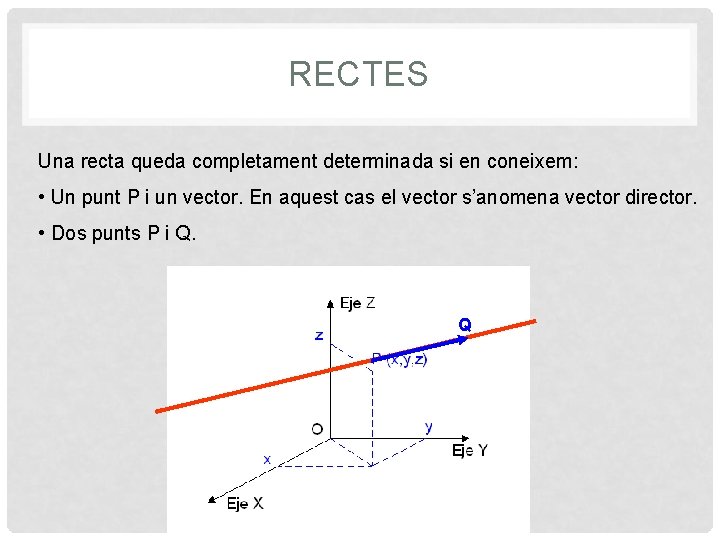
RECTES Una recta queda completament determinada si en coneixem: • Un punt P i un vector. En aquest cas el vector s’anomena vector director. • Dos punts P i Q. Q

EQUACIONS DE LA RECTA • Equació vectorial: • Equacions paramètriques: • Equació contínua:

EQUACIONS DE LA RECTA • Equacions implícites: si en l’equació contínua prenem dues de les igualtats i les multipliquem en creu, obtenim dues equacions lineals amb incògnites x, y i z Agrupant i reanomenant:

EXEMPLE TIPUS: EQUACIONS DE LA RECTA • Sigui la recta r que passa pel punt A(1, 3, 0) i té vector director determina les equacions vectorial, paramètriques, contínua i implícites. • Equació vectorial: • Equacions paramètriques: • Equació contínua: • Equació implícita: ordenant i agrupant

EQUACIÓ DE LA RECTA QUE PASSA PER 2 PUNTS • Expressa les equacions paramètriques i l’equació contínua de la recta que passa per A(4, -1, -6) i B(-5, 3, 0) Vector director: Equacions paramètriques: Equació contínua:

PUNTS ALINEATS • Determina si els punts A(4, -1, -6), B(-5, 3, 0) i C(2, -1, 2) estan alineats A, B i C estan alineats si pertanyen a la mateixa recta: Si C pertany a la recta que determinen A i B ha de complir la seva equació: No estan alineats

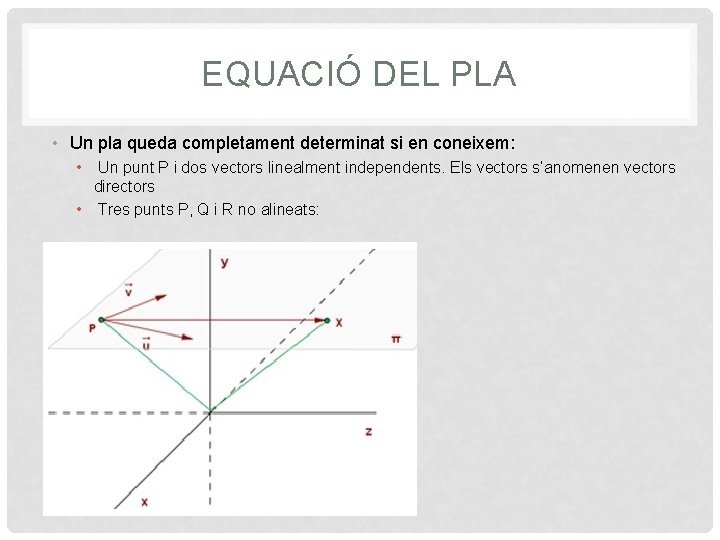
EQUACIÓ DEL PLA • Un pla queda completament determinat si en coneixem: • Un punt P i dos vectors linealment independents. Els vectors s’anomenen vectors directors • Tres punts P, Q i R no alineats:

EQUACIÓ DEL PLA • Equació vectorial: • Equacions paramètriques:

EQUACIÓ DEL PLA • Equació general o cartesiana: Equació general

EQUACIÓ DEL PLA QUE PASSA PER 3 PUNTS Siguin A(a 1, a 2, a 3), B(b 1, b 2, b 3) i C(c 1, c 2, c 3) tres punts no alineats de l’espai, llavors les equacions paramètriques es poden escriure: On P(x, y, z) és un punt qualsevol del pla. I com que AP, AB i AC són linealment dependents: Desenvolupant aquest determinant s’obté l’equació general del pla.

PUNTS COPLANARIS Siguin A(a 1, a 2, a 3), B(b 1, b 2, b 3), C(c 1, c 2, c 3) i D(d 1, d 2, d 3) quatre punts no alineats de l’espai, direm que són coplanaris si pertanyen al mateix pla:

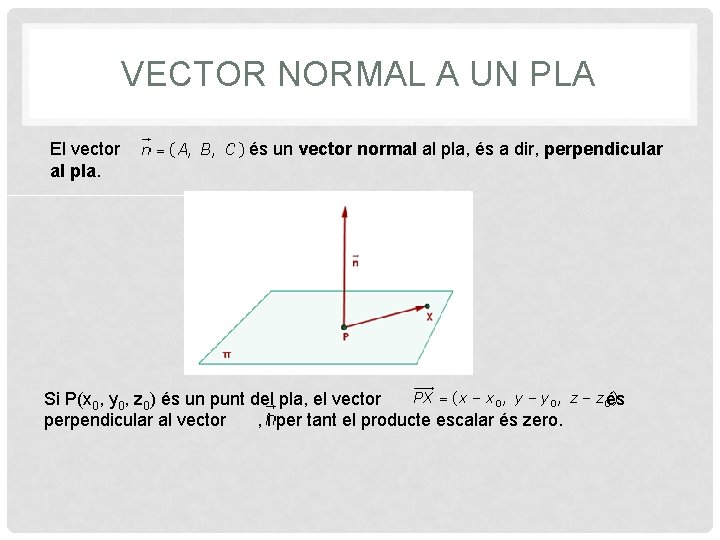
VECTOR NORMAL A UN PLA El vector és un vector normal al pla, és a dir, perpendicular al pla. Si P(x 0, y 0, z 0) és un punt del pla, el vector és perpendicular al vector , i per tant el producte escalar és zero.

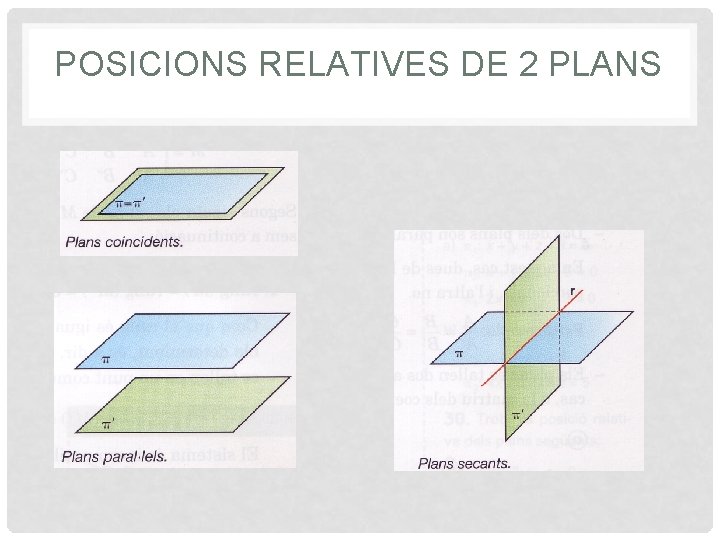
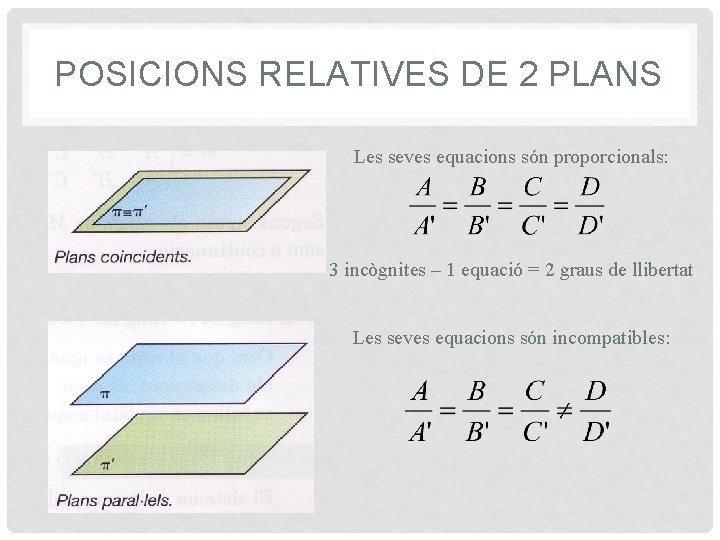
POSICIONS RELATIVES DE 2 PLANS

POSICIONS RELATIVES DE 2 PLANS Les seves equacions són proporcionals: 3 incògnites – 1 equació = 2 graus de llibertat Les seves equacions són incompatibles:

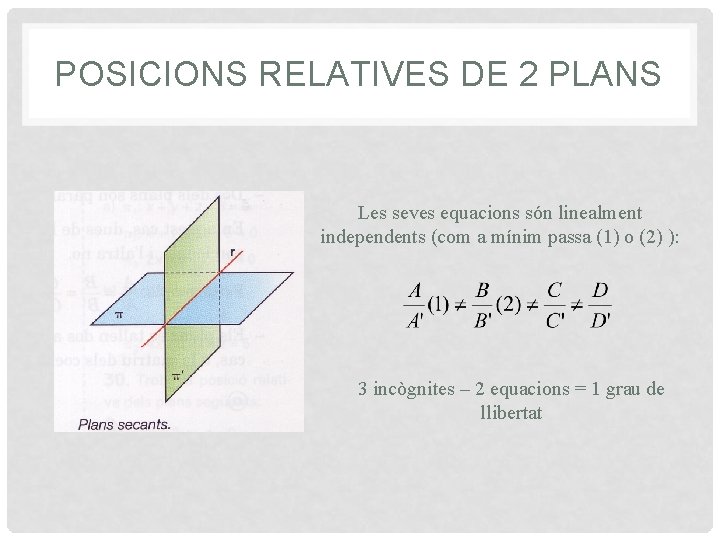
POSICIONS RELATIVES DE 2 PLANS Les seves equacions són linealment independents (com a mínim passa (1) o (2) ): 3 incògnites – 2 equacions = 1 grau de llibertat

POSICIÓ RELATIVA DE 3 PLANS Considerem 3 plans donats per les seves equacions generals: De manera que la matriu dels coeficients i la matriu ampliada:

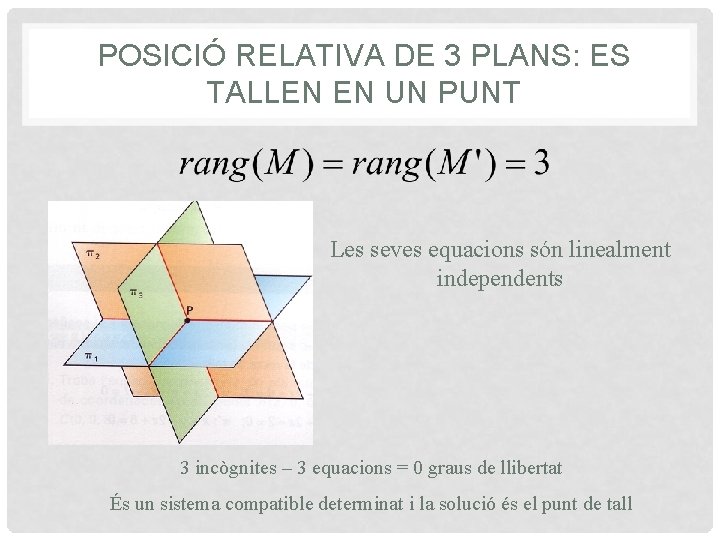
POSICIÓ RELATIVA DE 3 PLANS: ES TALLEN EN UN PUNT Les seves equacions són linealment independents 3 incògnites – 3 equacions = 0 graus de llibertat És un sistema compatible determinat i la solució és el punt de tall

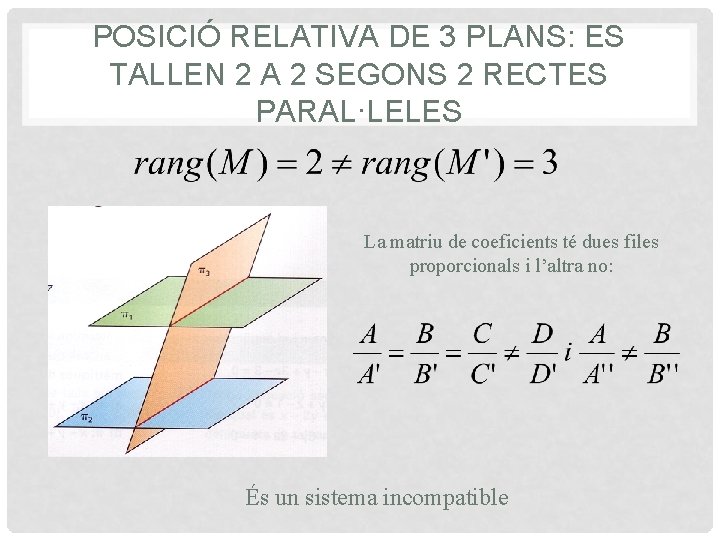
POSICIÓ RELATIVA DE 3 PLANS: ES TALLEN 2 A 2 SEGONS 2 RECTES PARAL·LELES La matriu de coeficients té dues files proporcionals i l’altra no: És un sistema incompatible

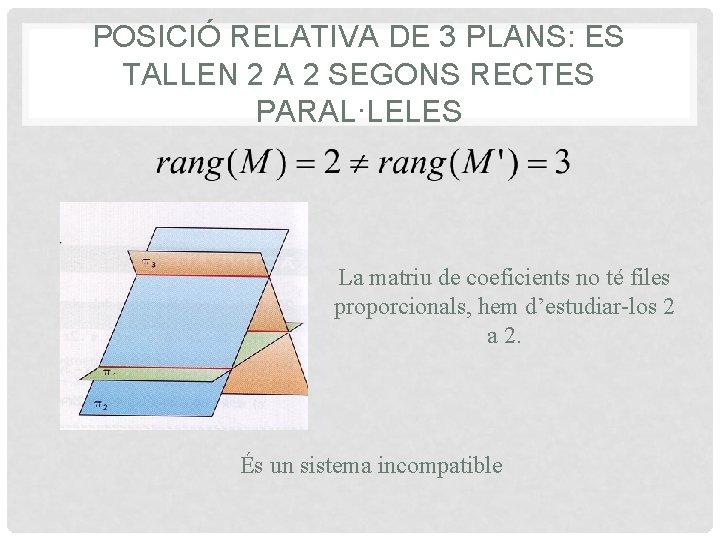
POSICIÓ RELATIVA DE 3 PLANS: ES TALLEN 2 A 2 SEGONS RECTES PARAL·LELES La matriu de coeficients no té files proporcionals, hem d’estudiar-los 2 a 2. És un sistema incompatible

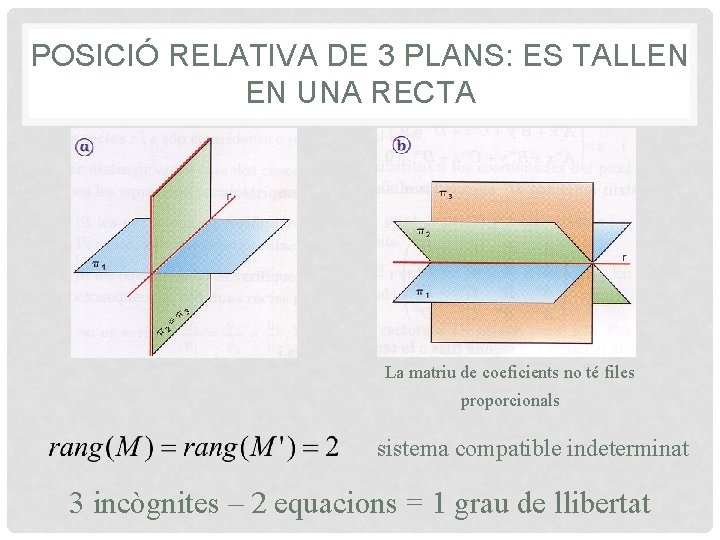
POSICIÓ RELATIVA DE 3 PLANS: ES TALLEN EN UNA RECTA La matriu de coeficients no té files proporcionals sistema compatible indeterminat 3 incògnites – 2 equacions = 1 grau de llibertat

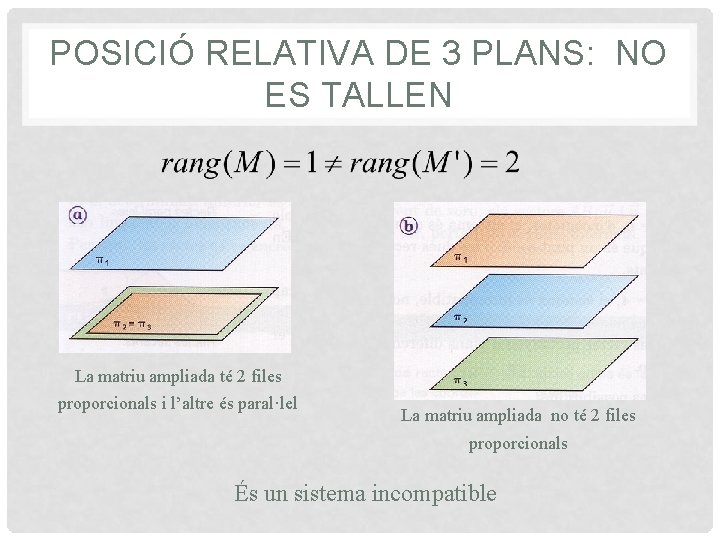
POSICIÓ RELATIVA DE 3 PLANS: NO ES TALLEN La matriu ampliada té 2 files proporcionals i l’altre és paral·lel La matriu ampliada no té 2 files proporcionals És un sistema incompatible

POSICIÓ RELATIVA DE 3 PLANS: COINCIDENTS sistema compatible indeterminat 3 incògnites – 1 equacions = 2 graus de llibertat

POSICIONS RELATIVES DE DUES RECTES Considerem 2 rectes determinades per les seves equacions generals: De manera que la matriu dels coeficients i la matriu ampliada:

POSICIONS RELATIVES DE DUES RECTES

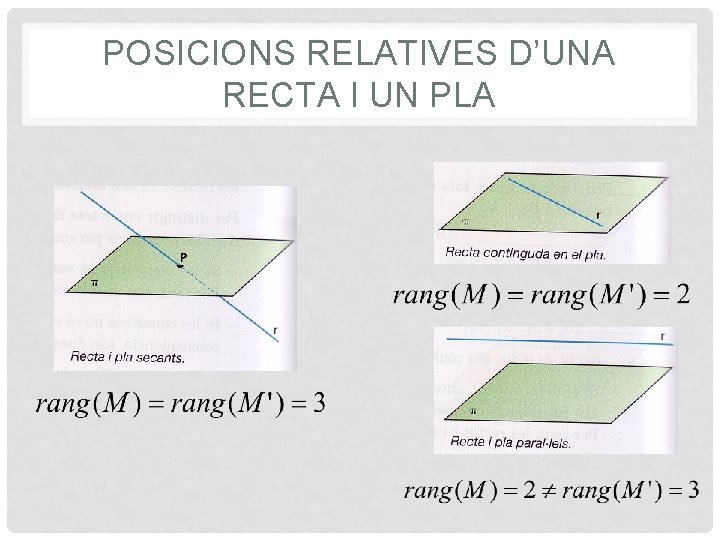
POSICIONS RELATIVES D’UNA RECTA I UN PLA Considerem 1 recta i un pla determinats per les seves equacions generals: De manera que la matriu dels coeficients i la matriu ampliada:

POSICIONS RELATIVES D’UNA RECTA I UN PLA