Chapter 9 Geometry Chapter 9 Geometry 9 1

Chapter 9: Geometry

Chapter 9: Geometry • • • 9. 1: Points, Lines, Planes and Angles 9. 2: Curves, Polygons and Circles 9. 3: Triangles (Pythagoras’ Theorem) 9. 4: Perimeter, Area and Circumference 9. 6: Transformational Geometry 9. 7: Non-Euclidean Geometry, Topology and Networks • 9. 8 Chaos and Fractals

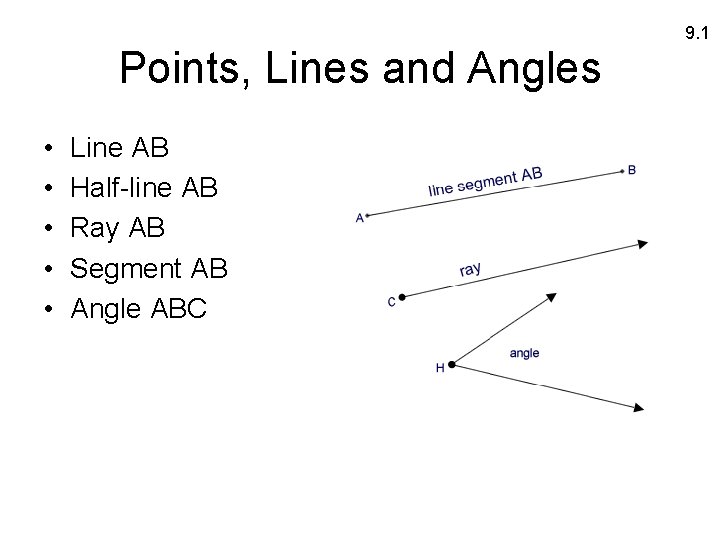
9. 1 Points, Lines and Angles • • • Line AB Half-line AB Ray AB Segment AB Angle ABC

Types of Angles • • • Acute Right Obtuse Straight Complementary Supplementary 9. 1

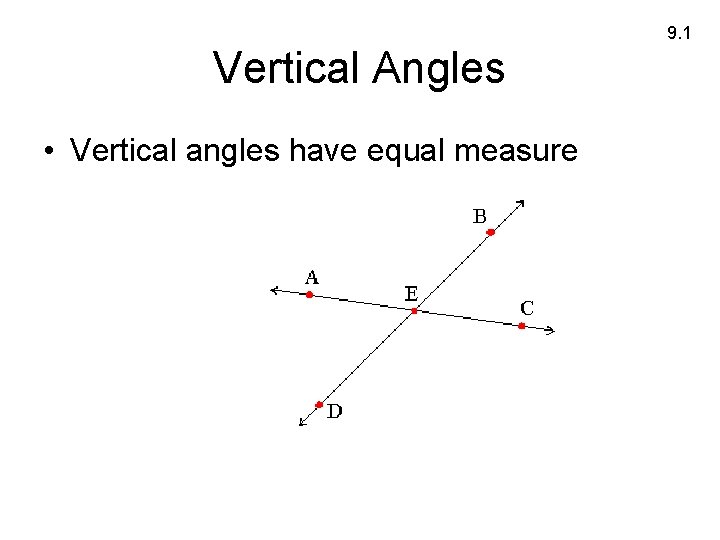
9. 1 Vertical Angles • Vertical angles have equal measure

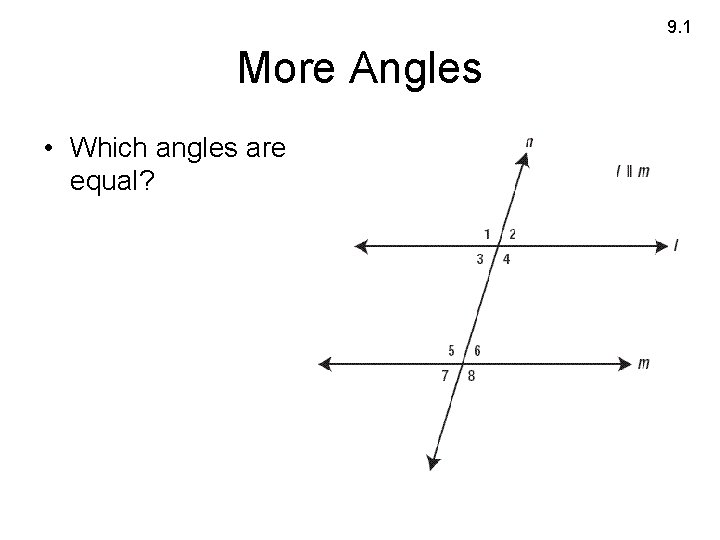
9. 1 More Angles • Which angles are equal?

Curves • Simple • Closed 9. 2

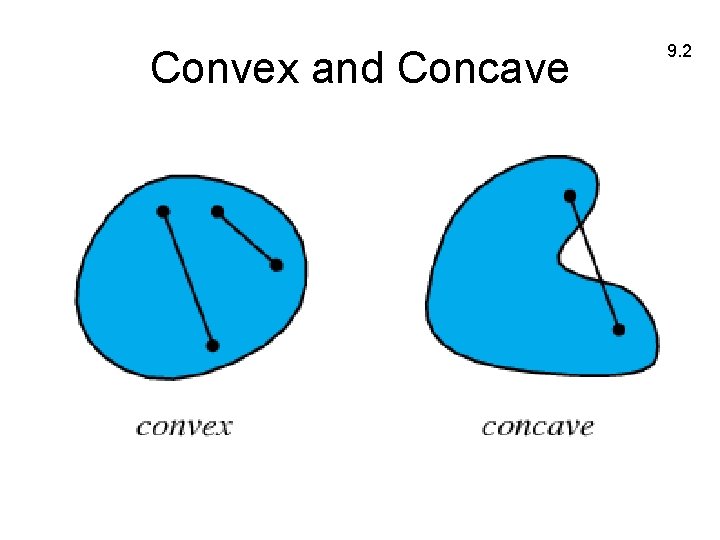
Convex and Concave 9. 2

Polygons • A polygon is a simple, closed curve made up of straight lines. • A regular polygon is convex with all sides equal and all angles equal. 9. 2

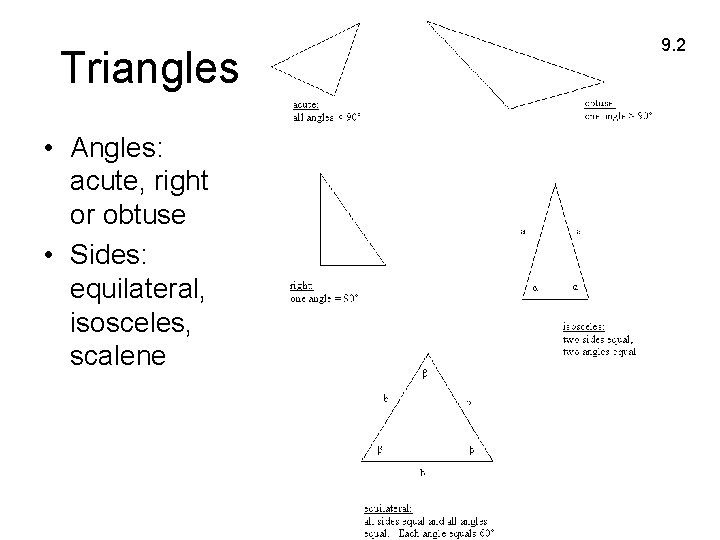
Triangles • Angles: acute, right or obtuse • Sides: equilateral, isosceles, scalene 9. 2

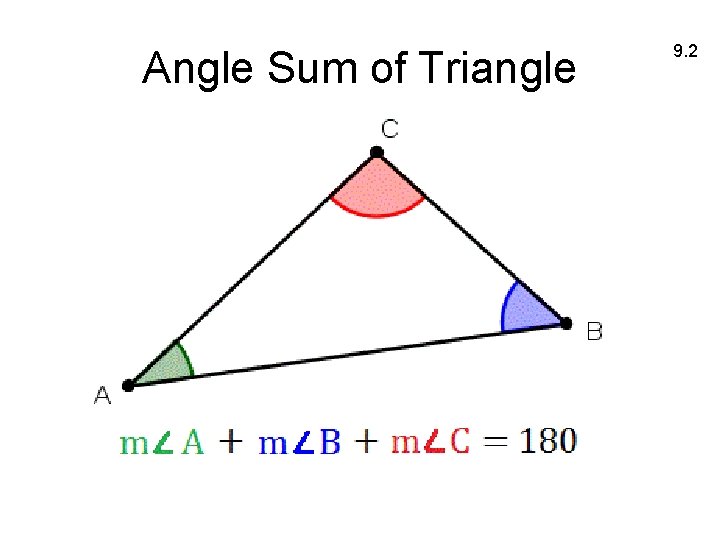
Angle Sum of Triangle 9. 2

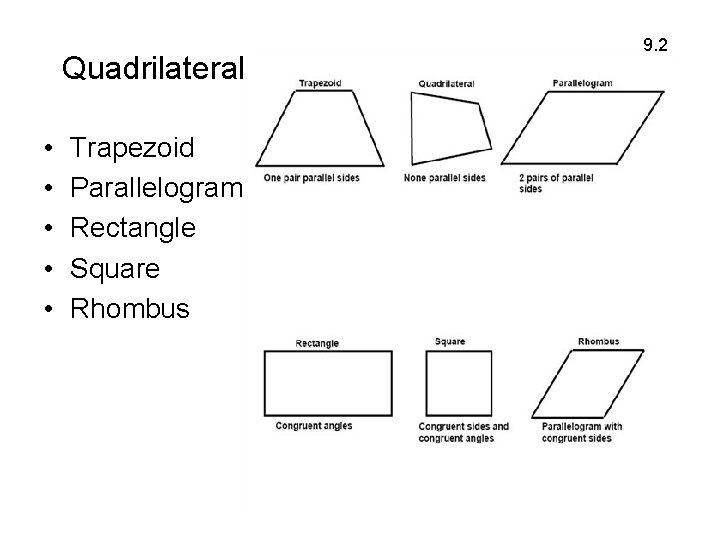
Quadrilaterals • • • Trapezoid Parallelogram Rectangle Square Rhombus 9. 2

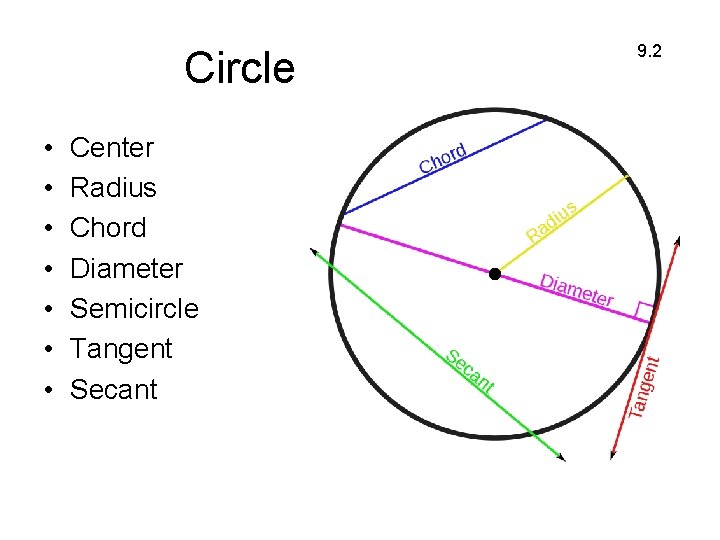
Circle • • Center Radius Chord Diameter Semicircle Tangent Secant 9. 2

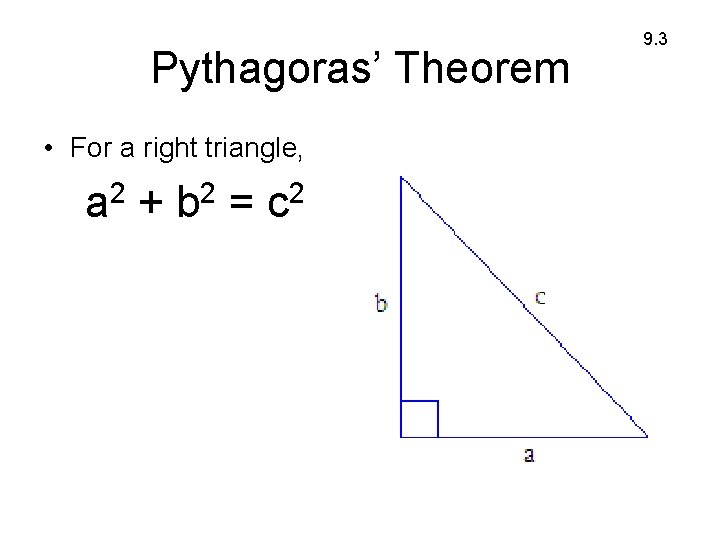
Pythagoras’ Theorem • For a right triangle, 2 a + 2 b = 2 c 9. 3

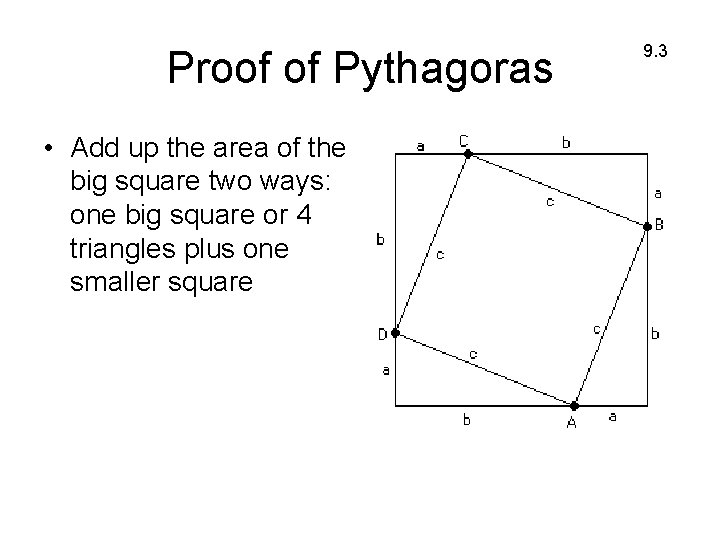
Proof of Pythagoras • Add up the area of the big square two ways: one big square or 4 triangles plus one smaller square 9. 3

Perimeter • The perimeter of a plane figure composed of line segments is the sum of the measures of the line segments, so the total length around the object. It is measured in linear units. 9. 4

Area 9. 4 • The area of a plane figure is the measure of the surface covered by the figure.

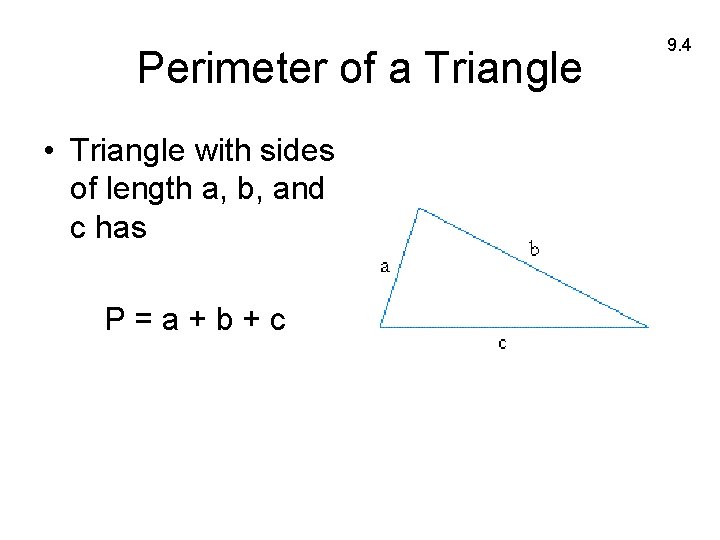
Perimeter of a Triangle • Triangle with sides of length a, b, and c has P=a+b+c 9. 4

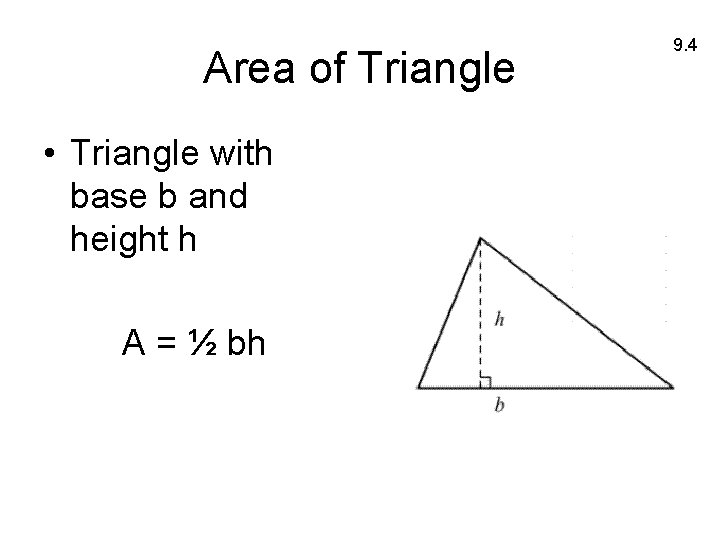
Area of Triangle • Triangle with base b and height h A = ½ bh 9. 4

Perimeter and Area of Rectangle • Rectangle with length l and width w has P = 2 l + 2 w = 2(l + w) A = lw 9. 3

9. 3 Perimeter and Area of Square • If all sides have length s, then P = 4 s A = s 2

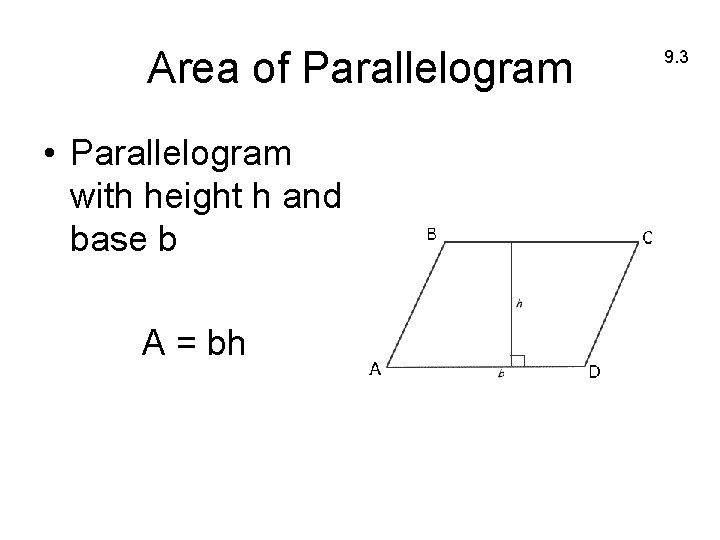
Area of Parallelogram • Parallelogram with height h and base b A = bh 9. 3

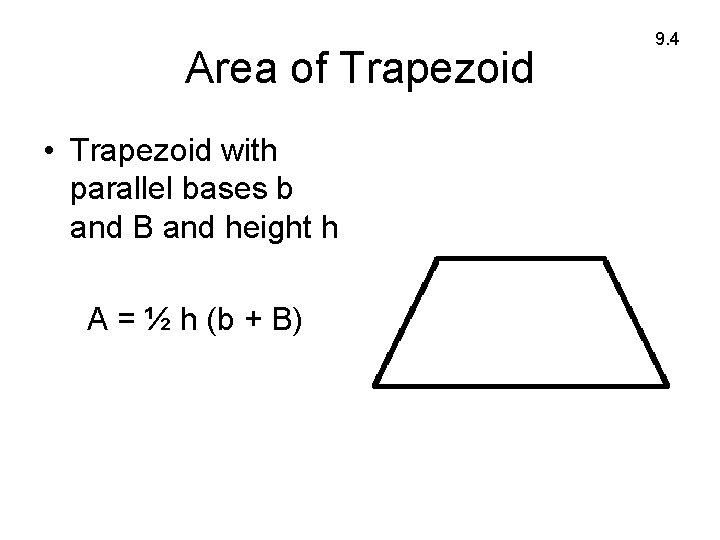
Area of Trapezoid • Trapezoid with parallel bases b and B and height h A = ½ h (b + B) 9. 4

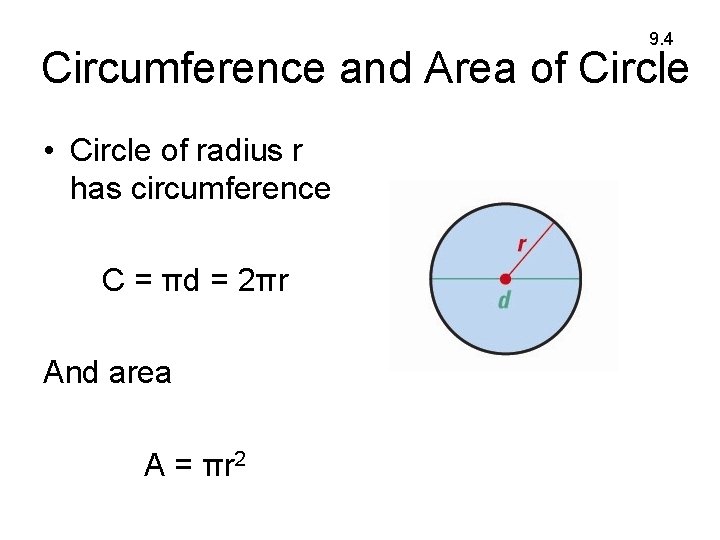
9. 4 Circumference and Area of Circle • Circle of radius r has circumference C = πd = 2πr And area A = πr 2

9. 6 Transformational Geometry • The investigation of how one geometric figure can be transformed into another • Reflections, rotations, translations and glide reflections

Reflections • The reflection of the point C across the line AB is the point C’ on the other side of the line segment such that CC’ is perpendicular to AB and C’ are the same distance from AB • AB is called the line of reflection, C’ is called the reflection image of C 9. 6

More on Reflections 9. 6 • If a point A is equal to its image point A’, then A is called an invariant point of the transformation. The only invariant points are on the line of reflection. • Three or more points that lie on the same line are said to be collinear. Reflections preserve collinearity. • Reflections also preserve distance. • Use symbol rm to denote reflection across line m

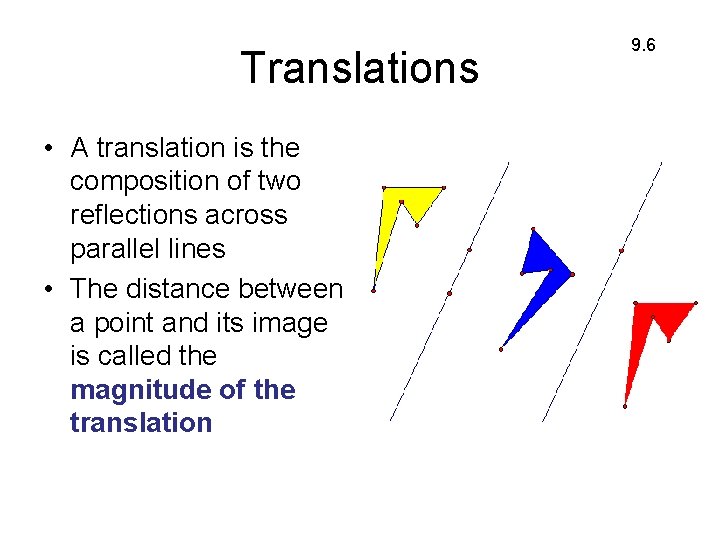
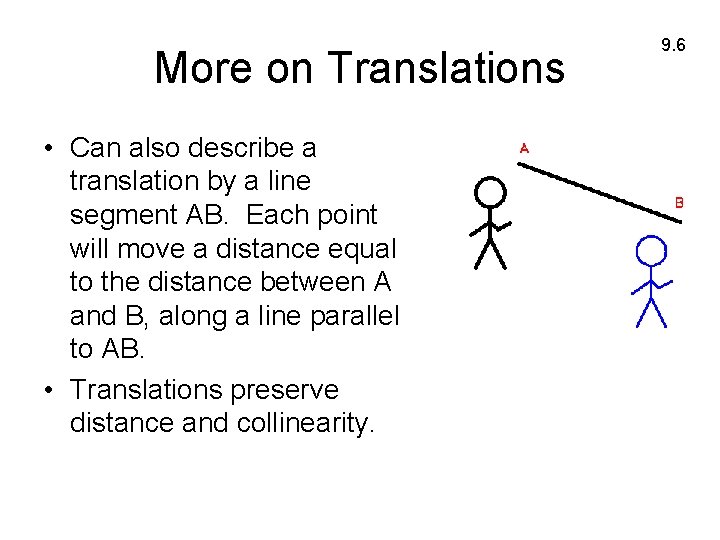
Translations • A translation is the composition of two reflections across parallel lines • The distance between a point and its image is called the magnitude of the translation 9. 6

More on Translations • Can also describe a translation by a line segment AB. Each point will move a distance equal to the distance between A and B, along a line parallel to AB. • Translations preserve distance and collinearity. 9. 6

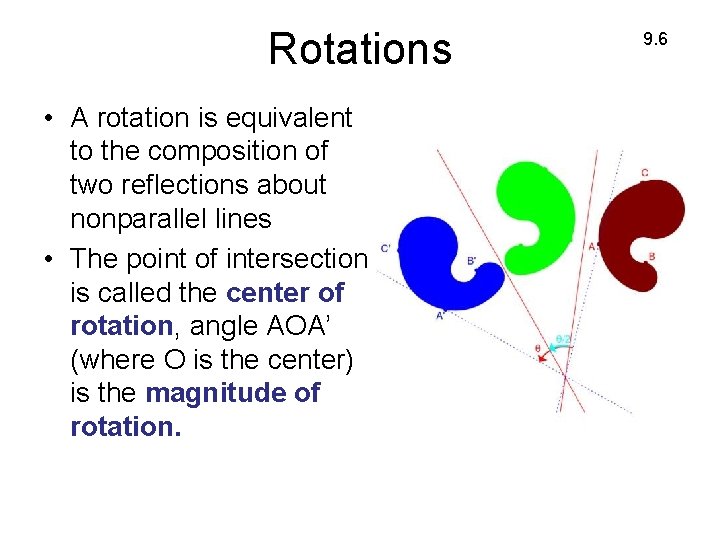
Rotations • A rotation is equivalent to the composition of two reflections about nonparallel lines • The point of intersection is called the center of rotation, angle AOA’ (where O is the center) is the magnitude of rotation. 9. 6

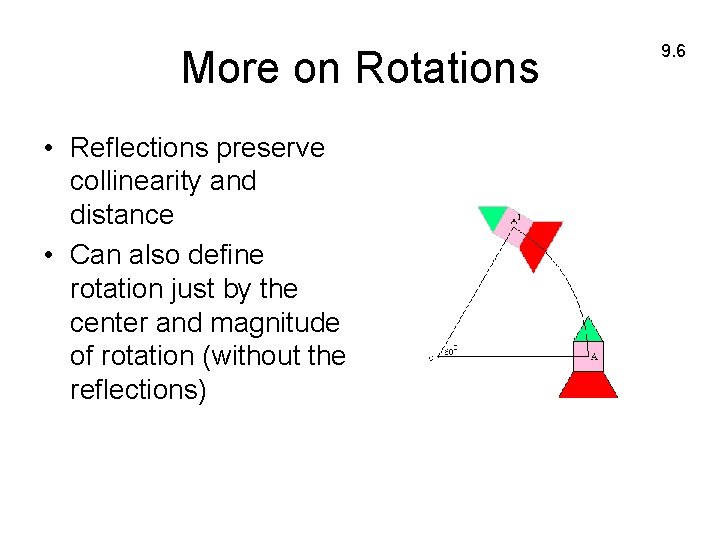
More on Rotations • Reflections preserve collinearity and distance • Can also define rotation just by the center and magnitude of rotation (without the reflections) 9. 6

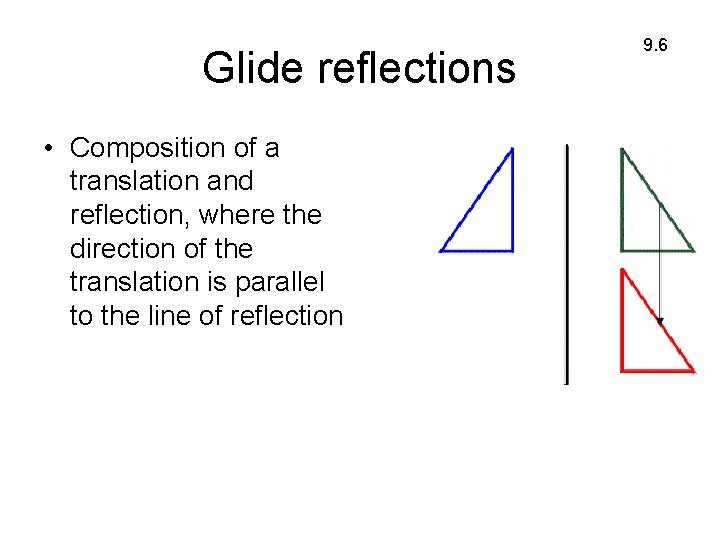
Glide reflections • Composition of a translation and reflection, where the direction of the translation is parallel to the line of reflection 9. 6

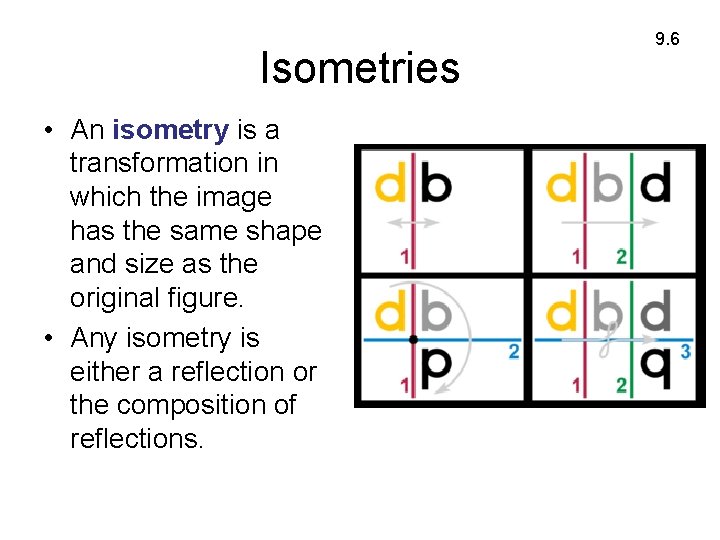
Isometries • An isometry is a transformation in which the image has the same shape and size as the original figure. • Any isometry is either a reflection or the composition of reflections. 9. 6

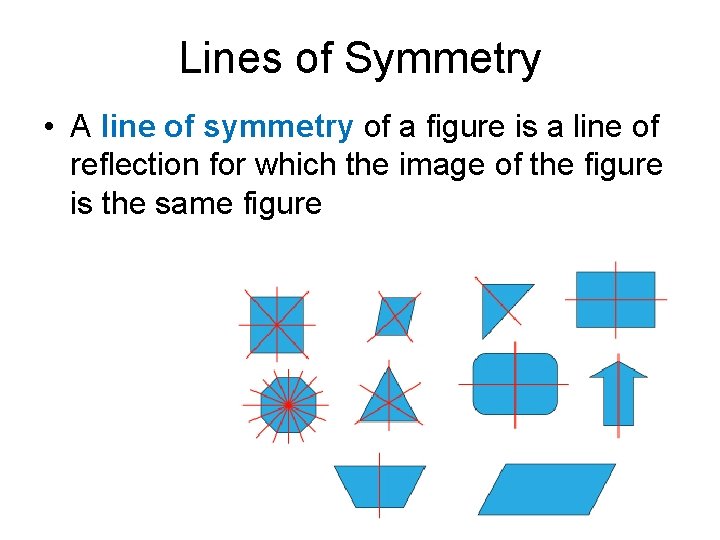
Lines of Symmetry • A line of symmetry of a figure is a line of reflection for which the image of the figure is the same figure

Euclid’s Postulates 1. Two points determine one and only one straight line 2. A straight line extends indefinitely far in either direction 3. A circle may be drawn with any given center and any given radius 4. All right angles are equal 5. Given a line k and a point P not on the line, there exists one and only one line m through P that is parallel to k 9. 7

Euclid’s Fifth Postulate (parallel postulate) • If two lines are such that a third line intersects them so that the sum of the two interior angles is less than two right angles, then the two lines will eventually intersect 9. 7

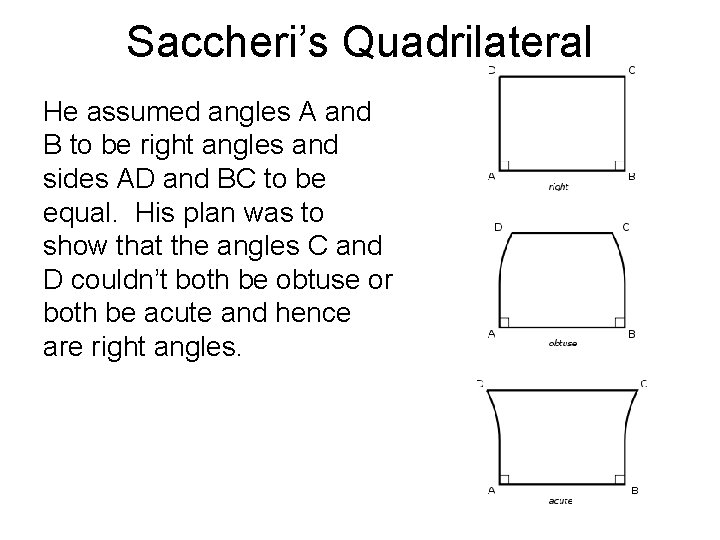
Saccheri’s Quadrilateral He assumed angles A and B to be right angles and sides AD and BC to be equal. His plan was to show that the angles C and D couldn’t both be obtuse or both be acute and hence are right angles.

Non-Euclidean Geometry 9. 7 • The first four postulates are much simpler than the fifth, and for many years it was thought that the fifth could be derived from the first four • It was finally proven that the fifth postulate is an axiom and is consistent with the first four, but NOT necessary (took more than 2000 years!) • Saccheri (1667 -1733) made the most dedicated attempt with his quadrilateral • Any geometry in which the fifth postulate is changed is a non-Euclidean geometry

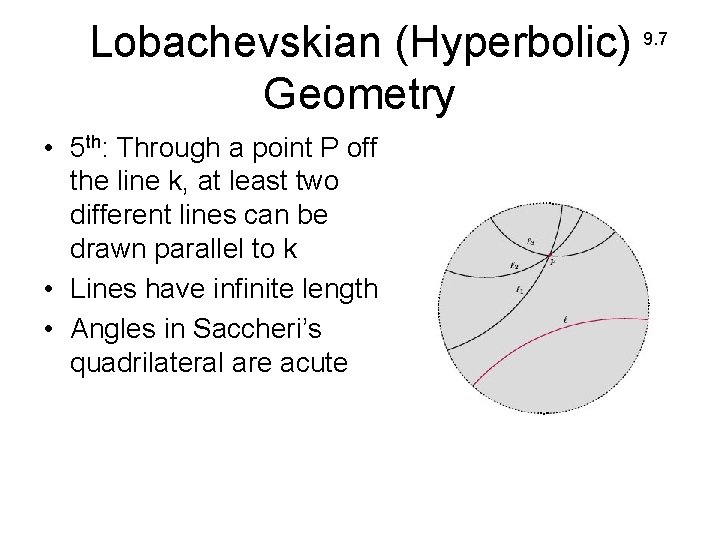
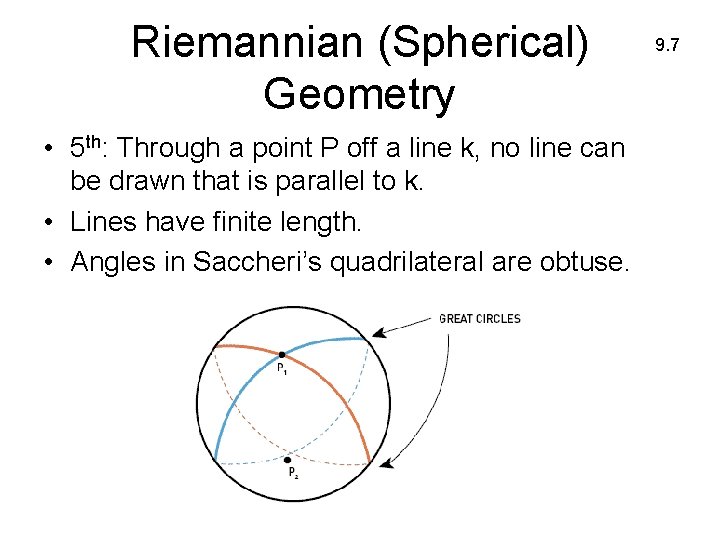
Lobachevskian (Hyperbolic) 9. 7 Geometry • 5 th: Through a point P off the line k, at least two different lines can be drawn parallel to k • Lines have infinite length • Angles in Saccheri’s quadrilateral are acute

Riemannian (Spherical) Geometry • 5 th: Through a point P off a line k, no line can be drawn that is parallel to k. • Lines have finite length. • Angles in Saccheri’s quadrilateral are obtuse. 9. 7

Topology 9. 7 • Suppose we could study objects that could be stretched, bent, or otherwise distorted without tearing or scattering. This is topology. • Topology investigates basic structure like number of holes or how many components.

Topologically equivalent • A donut and a coffee cup are equivalent while a muffin and coffee cup are not. 9. 7

9. 7 Exercise: Letters of Alphabet ABCDEFGH IJKLMNOP QRSTUVWX YZ

9. 7 Interesting Topological Surfaces Moebius Strip Klein Bottle

Orientability and Genus 9. 7 • A topological surface is orientable if you can determine the outside and inside. • Any orientable, compact (finite size) surface is determined by its number of holes (called the genus).

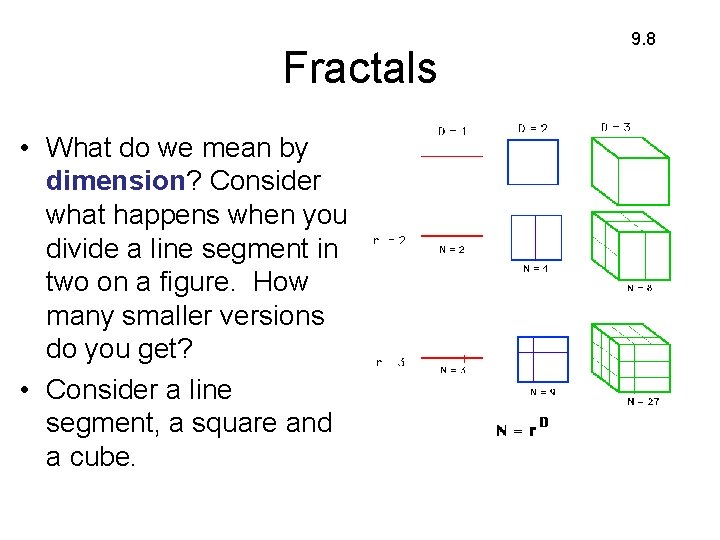
Fractals • What do we mean by dimension? Consider what happens when you divide a line segment in two on a figure. How many smaller versions do you get? • Consider a line segment, a square and a cube. 9. 8

9. 8 Self-similarity • An object is self-similar if it can be formed from smaller versions of itself (with no gaps or overlap) • A square is self-similar, a circle is not. • Many objects in nature have self-similarity.

More self-similarity in Nature 9. 8

Self-similar fractals 9. 8 • Start with some basic geometrical object like a line segment or triangle and perform some operation. Then repeat the process indefinitely (this is called iterating). Each iteration produces a more complicated object. • The fractal dimension D can be found by considering the scaling at each iteration, where r is the scaling amount and N is the number of smaller pieces. r. D = N so D = ln N/ln r

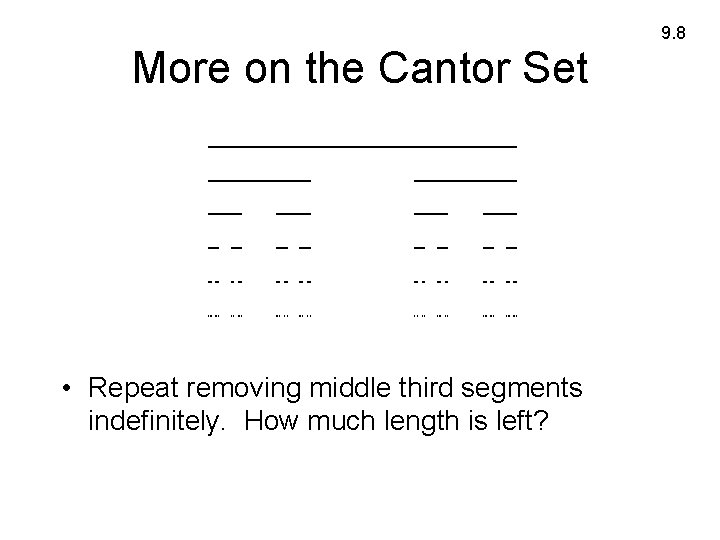
Cantor Set • Start with the line segment of length 1 between 0 and 1. Remove the middle third segment. Repeat this process to the remaining two line segments. • At each iteration you scale down by 3 to get 2 new pieces. What is the fractal dimension? 9. 8

9. 8 More on the Cantor Set • Repeat removing middle third segments indefinitely. How much length is left?

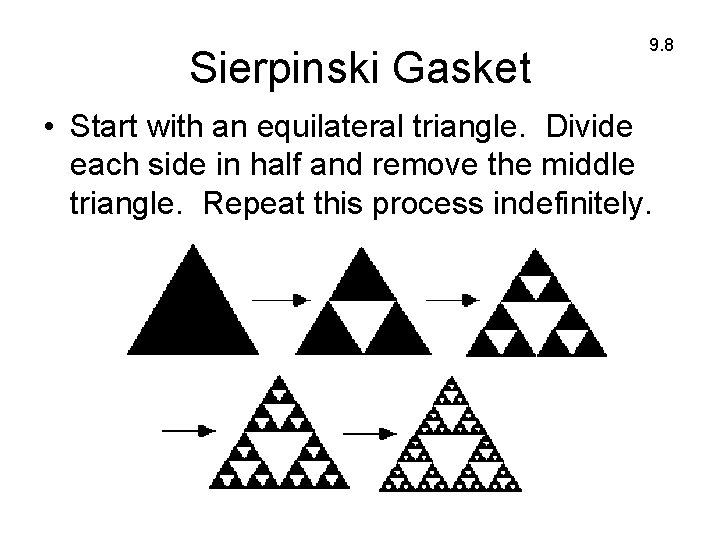
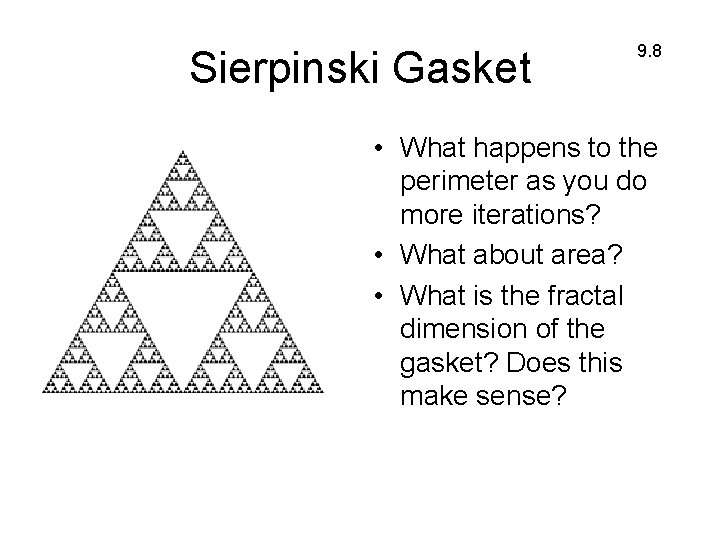
Sierpinski Gasket 9. 8 • Start with an equilateral triangle. Divide each side in half and remove the middle triangle. Repeat this process indefinitely.

Sierpinski Gasket 9. 8 • What happens to the perimeter as you do more iterations? • What about area? • What is the fractal dimension of the gasket? Does this make sense?

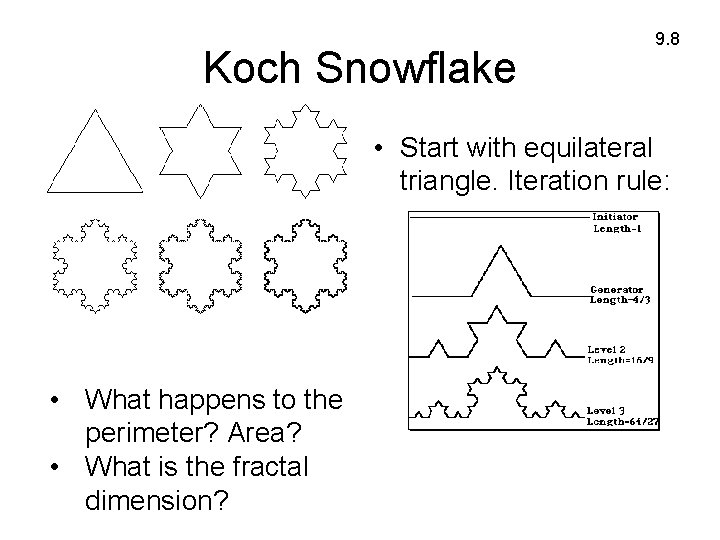
Koch Snowflake 9. 8 • Start with equilateral triangle. Iteration rule: • What happens to the perimeter? Area? • What is the fractal dimension?