Geometry Chapter 1 Types of Geometry Point Line

Geometry Chapter 1

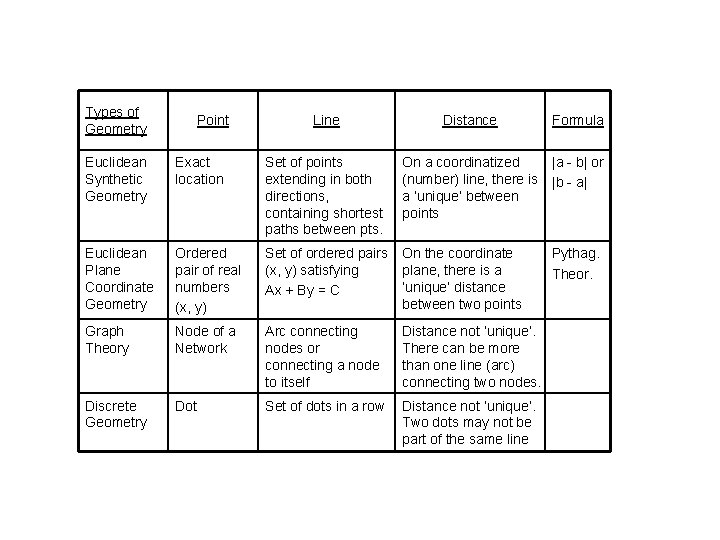
Types of Geometry Point Line Distance Formula Euclidean Synthetic Geometry Exact location Set of points extending in both directions, containing shortest paths between pts. On a coordinatized |a - b| or (number) line, there is |b - a| a ‘unique’ between points Euclidean Plane Coordinate Geometry Ordered pair of real numbers (x, y) Set of ordered pairs (x, y) satisfying Ax + By = C On the coordinate plane, there is a ‘unique’ distance between two points Graph Theory Node of a Network Arc connecting nodes or connecting a node to itself Distance not ‘unique’. There can be more than one line (arc) connecting two nodes. Discrete Geometry Dot Set of dots in a row Distance not ‘unique’. Two dots may not be part of the same line Pythag. Theor.

Graph Theory - Nodes in a Network Nodes are connected by one or more Arcs. Odd nodes - have an odd number of connecting arcs Even nodes - have an even number of connecting arcs A network is traversable if does not have more than two odd nodes 2 or less). A network is not traversable if it has more than two odd nodes (3 or more).

Undefined • Terms (in this book)- point, Definitions Using Undefined Terms: Figure - a set of points Space - the set of all points Collinear - three or more points that are contained on the same line Plane Figure - a set of points that are all in one plane Coplanar - four or more points that are contained on the same plane line, plane

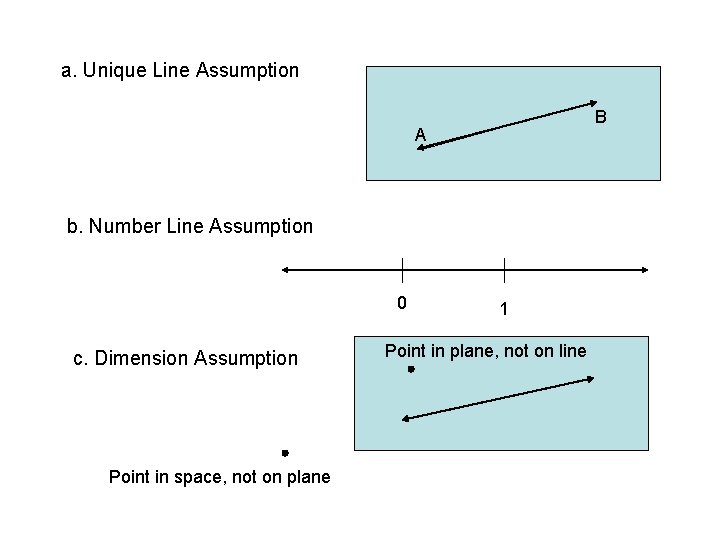
Point-Line-Plane Postulate (Euclidean Geometry) a. Unique Line Assumption: Through any two points there is exactly one line. If two points are in the same plane, the line containing them is in the plane. b. Number Line Assumption: Every line is a set of points (that can be put in a one-to-one correspondence with the real numbers), with one point on the line corresponding to 0 and another point corresponding to 1. c. Dimension Assumption: 1. There at least two points in space. 2. Given a line in a plane, there is at least one point on the plane that is not on the line. 3. Given a plane in space, there is at least one point in space that is not in the plane.

a. Unique Line Assumption B A b. Number Line Assumption 0 c. Dimension Assumption Point in space, not on plane 1 Point in plane, not on line

Equation of a Line Standard Form: Oblique Line (not horizontal or vertical) Ax + By = C ex. 4 x + 3 y = 7 (A, B, and C are integers, A is positive) Horizontal Line By = C ex. 3 y = 9 --> y=3 Vertical Line Ax = C ex. 4 x = 8 --> x=2

Equation of a Line Slope-Intercept Form: Oblique Line (not horizontal or vertical) y = mx + b ex. y = 5 x - 2 m = slope b = y-intercept (0, b) Horizontal Line y=b ex. y = 6 b = a real number Vertical Line x=c ex. x = -2 c = a real number

Slope of a Line Slope Formula: m= y 2 - y 1 x 2 - x 1 Oblique Line (not horizontal or vertical) slope positive (line rises left to right): slope negative (line falls left to right): +/+ or -/+/- or -/+ Horizontal Line Slope = 0 (‘y’ value remains constant, x varies) Vertical Line Slope - undefined (‘x’ value remains constant, y varies)

Standard Form --> Slope-Intercept Form Ax + By = C y = mx + b Step 1: add or subtact ‘x’ term from both sides of the equation ex. 4 x + 3 y = 9 -4 x ----3 y = -4 x + 9

Standard Form --> Slope-Intercept Form Ax + By = C y = mx + b Step 2: divide all terms by the coefficient of the ‘y’ term ex. 3 y = -4 x + 9 ---- ---3 3 3 y = -4/3 x + 3 Slope = m = -4/3 y-intercept - (0, 3)

Graphing an equation in Slope-Intercept Form Step 1: Graph the y-intercept point (0, b) on the y-axis Step 2: Use the slope to plot a second point Step 3: Connect the points with a line (<---->) Step 4: Check your slope (positive or negative) a. Positive slopes - rise from left to right ( / ) b. Negative slopes - fall from left to right ( )

Give the equation of a line through two given points Given: (x 1, y 1), (x 2, y 2) ex. (2, 1), (6, 4) Step 1: Calculate the slope (using slope formula) Step 2: Put slope into the slope-intercept equation form y = mx + b ex. y = 3/4 x + b Step 3: Use one of the points to solve for ‘b’ y 1 = m(x 1) + b ex. 1 = 3/4(2) + b 1 = 3/2 + b 1 - 3/2 = b, b = -1/2 Step 4: Write equation y = 3/4 x - 1/2

Solving a system of two equations Given two equations (in standard form): 3 x + 2 y = 6 --> 3 x + 2 y = 6 x - y =7 --> -3(x - y = 7) distribute -3 x + 3 y = -21 Add first equation 3 x + 2 y = 6 -----------Solve for one variable 5 y = -15 y = -3 Plug ‘value’ into one of the original equations

Solving a system of two equations Plug ‘value’ into one of the original equations and solve for the other variable. x-y=7 x - (-3) = 7 x+ 3= 7 x=7 -3 x=4 Check solution y = -3 Solution (4, -3) 3(4) + 2(-3) = 6 12 - 6 = 6 (true)

Intersecting, Parallel, and Perpendicular Lines Intersecting Lines a. same line (same slope, same y-intercept) b. different lines (different slopes) Parallel Lines a. same slope, but different y-intercepts Perpendicular Lines a. (slope of first line) * (slope of second line) = -1 the slopes are negative reciprocals (ex. 2/3 * -3/2 = -1)

One, Two, and Three Dimensional One Dimensional corresponds to Collinear: (single axis) ex. A number line, a taught string Two Dimensional corresponds to Coplanar: (coordinate plane) ex. The top of a table, the chalkboard Three Dimensional (xy plane, yz plane, and xz plane combined) ex. Ice cream cone, basketball, house

Triangle Inequality Postulate (∆ABC) - sides AB, BC, and CA AB + BC > CA BC + CA > AB CA + AB > BC ex. 6, 5, 7 6 + 5 > 7 (true) 5 + 7 > 6 (true) 7 + 6 > 5 (true) If one of the inequalities is not true, then the points will not form a triangle (ex. 6, 5, and 11 cannot be the lengths of the sides of a triangle).