Line Drawing by Algorithm Line Drawing Algorithms Line

Line Drawing by Algorithm

Line Drawing Algorithms • Line drawn as pixels • Graphics system – Projects the endpoints to their pixel locations in the frame buffer (screen coordinates as integers) – Finds a path of pixels between the two – Loads the color – Plots the line on the monitor from frame buffer (video controller) – Rounding causes all lines except horizontal or vertical to be displayed as jigsaw appearance (low resolution) – Improvement: high resolution, or adjust pixel intensities on the line path.

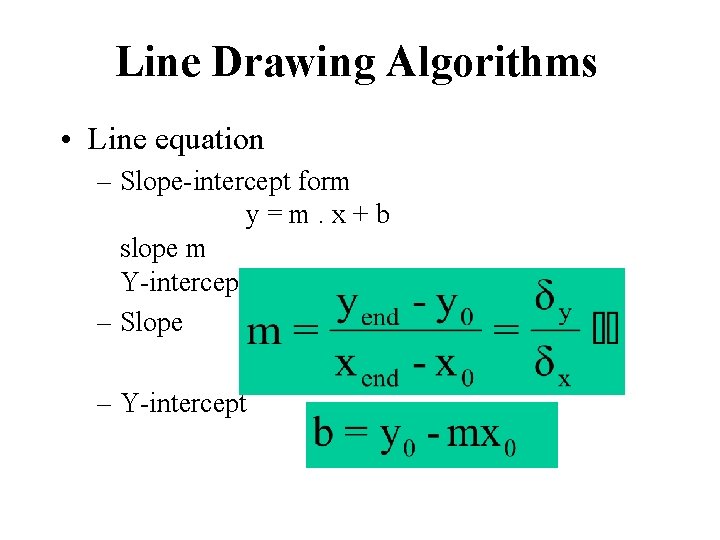
Line Drawing Algorithms • Line equation – Slope-intercept form y = m. x + b slope m Y-intercept b – Slope – Y-intercept

Line Drawing Algorithms • DDA (Digital Differential Analyzer) – Scan conversion line algorithm – Line sampled at regular intervals of x, then corresponding y is calculated – From left to right

Line Drawing Algorithms void line. DDA (int x 0, int y 0, int x. End, int y. End) { int dx = x. End - x 0, dy = y. End - y 0, steps, k; float x. Increment, y. Increment, x = x 0, y = y 0; if (fabs (dx) > fabs (dy)) steps = fabs (dx); else steps = fabs (dy); x. Increment = float (dx) / float (steps); y. Increment = float (dy) / float (steps); set. Pixel (round (x), round (y)); for (k = 0; k < steps; k++) { x += x. Increment; y += y. Increment; set. Pixel (round (x), round (y)); } }

Line Drawing Algorithms • Advantage – Does not calculate coordinates based on the complete equation (uses offset method) • Disadvantage – Round-off errors are accumulated, thus line diverges more and more from straight line – Round-off operations take time • Perform integer arithmetic by storing float as integers in numerator and denominator and performing integer artithmetic.

Observation on lines. while( n-- ) { draw(x, y); move right; if( below line ) move up; }

Line Drawing Algorithms • Bresenham’s line drawing – Efficient line drawing algorithm using only incremental integer calculations – Can be adapted to draw circles and other curves • Principle – Vertical axes show scan line positions – Horizontal axes show pixel columns – At each step, determine the best next pixel based on the sign of an integer parameter whose value is proportional to the difference between the vertical separations of the two pixel positions from the actual line.

Bresenham’s Algorithm • Improve upon DDA algorithm to use integer arithmetic only. • Applicable to circle drawing too. We discuss only the line drawing here. • An Accurate and efficient raster line generating Algo. And scan converts lines using only incrementa 1 integer calculations that can be adapted to display circles and other curves

Testing for the side of a line. • Need a test to determine which side of a line a pixel lies. • Write the line in implicit form: • Easy to prove. Y=m*X+Cnts below.

Decision Variables • Variables a and b record the distances to the pixel centers of (i+1, j) and (i+1, j+1) • If d 1 < d 2, then y=j • If d 1 > d 2, then y= j+1

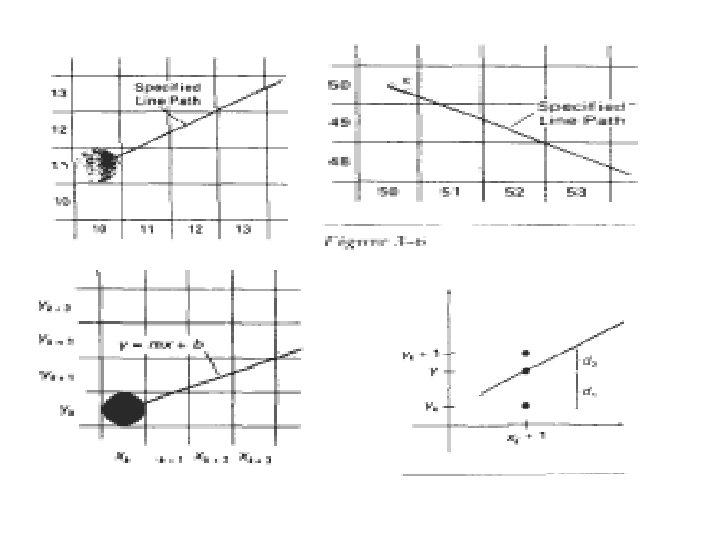
• The vertical axes show-scan-line positions, and the horizontal axes identify pixel columns. • Sampling at unit x intervals in these examples, we need to decide which of two possible pixel positions is closer to the line path at each sample step. Starting from the left endpoint we need to determine at the next sample • position whether to plot the pixel at position (11, 11) or the one at (11, 12) Line with negative slope-line path starting from the left endpoint at pixel position (50, 50). In this one, do we select the next pixel position as (51, 50)or as (51, 49)? These questions are answered with Bresenham's line algorithm by testing the sign of an integer parameter, whose value is proportional to the difference between the separations of the two pixel positions from the actual line path. • we- first consider the scanconversion process for lines with positive slope less than 1. Pixel positions along a line path are then determined by sampling at unit x intervals. Starting from the left end • point (x 0, yo) of a given line, we step to each successive column ( x position) and plot the pixel whose scan-line y value is closest to the line path. • demonstrates the Kh step in this process. Assuming we have determined that the pixel at (xk, yk) is to be displayed, we next need to decide which pixel to plot in • column x k + 1, . Our choices are the pixels at positions ( Xk+l, yk) and (xk+l, yk+l). • At sampling position xk+l, we label vertical pixel separations from the • mathematical line path as d 1 and d 2

• Y co-ordinate at column Xk+1 can be calculated as Y=m(Xk+1)+b then • D 1=y-yk=m(xk+1)+b-yk • D 2=(Yk+1) – y=Yk+1 –m(Xk+1)-b • Difference in these two sepration is • D 1 -D 2=2 m(Xk+1)-2 Yk+2 b-1 • Decision Parameter Pk( Kth iteration) Pk=DX(d 1 -d 2)=2 Dy * Xk-2 Dx * Yk+C Note Pk has Same Sign as d 1 -d 2 Sine DX>1, C is constant & C=2 Dy+Dx(2 b-1) is Independent of Pixel Position , Ignored In recursive cal of Pk Pk+1 can be calculated then Recursive Pk+1 be as Pk+1=Pk+2 Dy-2 Dx(Yk+1 - Yk) then Po=2 Dy-Dx

void lineares (int xa , Int ya , int x b , int yb) (int dx = a b s ( x a - x b) , dy = abs (ya - yb); int p = 2 * dy - d x ; int two. Dy = 2 * dy, two. Dy. Dx = 2 *(dy - dx ) ; int x , y, x. End: / * Determine which point to use a s start, which as end * / if ( x a > x b ) {x = x b ; Y = yb; x. End = x a ; } else {x = xa; Y = ya; x. End = xb; } setpixel ( x , y); while (x < x. End) { x++; if (p < 0 ) p+= two. Dy; else {y + + ; P += two. Dy. Dx; } setpixel ( x , y); }}