ANOVA Experimental Design and Analysis of Variance Mc



















- Slides: 28

ANOVA Experimental Design and Analysis of Variance Mc. Graw-Hill/Irwin Copyright © 2003 by The Mc. Graw-Hill Companies, Inc. All rights reserved. 10 -1 of 29

Experimental Design and Analysis of Variance 10. 1 10. 2 10. 3 10. 4 Basic Concepts of Experimental Design One-Way Analysis of Variance The Randomized Block Design Two-Way Analysis of Variance 10 -2 of 29

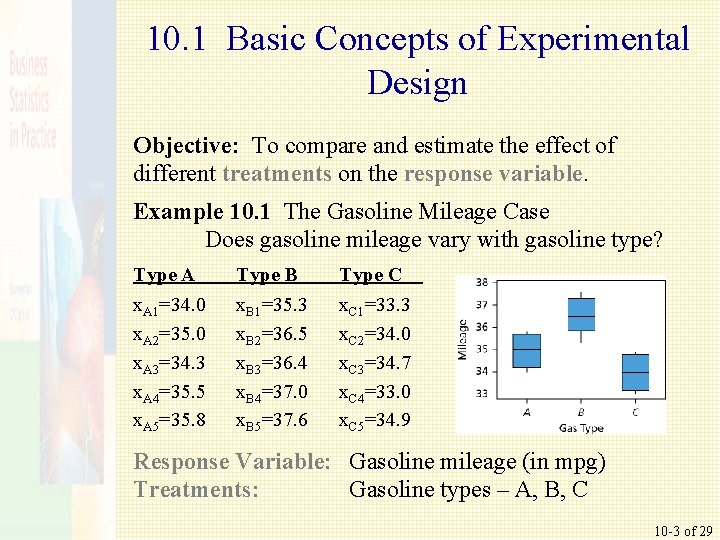
10. 1 Basic Concepts of Experimental Design Objective: To compare and estimate the effect of different treatments on the response variable. Example 10. 1 The Gasoline Mileage Case Does gasoline mileage vary with gasoline type? Type A Type B Type C x. A 1=34. 0 x. A 2=35. 0 x. A 3=34. 3 x. A 4=35. 5 x. A 5=35. 8 x. B 1=35. 3 x. B 2=36. 5 x. B 3=36. 4 x. B 4=37. 0 x. B 5=37. 6 x. C 1=33. 3 x. C 2=34. 0 x. C 3=34. 7 x. C 4=33. 0 x. C 5=34. 9 Response Variable: Gasoline mileage (in mpg) Treatments: Gasoline types – A, B, C 10 -3 of 29

10. 2 One-Way Analysis of Variance Are there differences in the mean response m 1, m 2, …, mp associated with the p treatments? H 0: m 1 = m 2 = … = m p Ha: At least two of the m 1, m 2, …, mp differ Or, is the betweentreatment variability large compared to the within-treatment variability? 10 -4 of 29

Partitioning the Total Variability in the Response Total Variability = Between Treatment Variability Total Sum of Squares = Treatment Sum + of Squares SSTO = SST p ni 2 = (x x ) åå ij i=1 j=1 p 2 n ( x x ) åi i i=1 + Within Treatment Variability + + Error Sum of Squares SSE p ni 2 (x x ) åå ij i i=1 j=1 10 -5 of 29

F Test for Difference Between Treatment Means H 0: m 1= m 2 =…= mp (no treatment effect) Ha: At least two of the m 1, m 2, …, mp differ Test Statistic: Reject H 0 if F > F or p-value < F is based on p-1 numerator and n-p denominator degrees of freedom. 10 -6 of 29

The One-Way Analysis of Variance Table Source Degrees of Freedom Sum of Squares Mean Squares F Statistic Treatments p-1 SST MST = SST p-1 F = MST MSE Error n-p SSE MSE = SSE n-p Total n-1 SSTO Example 10. 5 The Gasoline Mileage Case (Excel Output) 10 -7 of 29

Pairwise Comparisons, Individual Intervals Individual 100(1 - a)% confidence interval for mi - mh t /2 is based on n-p degrees of freedom. Example 10. 6 The Gasoline Mileage Case (A vs B , = 0. 05) 10 -8 of 29

Pairwise Comparisons, Simultaneous Intervals Tukey simultaneous 100(1 - a)% confidence interval for mi - mh q is the upper percentage point of the studentized range for p and (n-p) from Table A. 9. m denotes common sample size. Example 10. 6 The Gasoline Mileage Case (A vs B, = 0. 05) 10 -9 of 29

Estimation of Individual Treatment Means Individual 100(1 - a)% confidence interval for mi t /2 is based on n-p degrees of freedom. Example 10. 6 The Gasoline Mileage Case (Type B , = 0. 05) 10 -10 of 29

10. 3 The Randomized Block Design A randomized block design compares p treatments (for example, production methods) on each of b blocks (or experimental units; for example, machine operators. ) A generalization of the paired difference design, this design controls for variability in experimental units by comparing each treatment on the same (not independent) experimental units. Treatments 1 1 2. . . p Blocks 2 3… b xij = response from treatment i and block j 10 -11 of 29

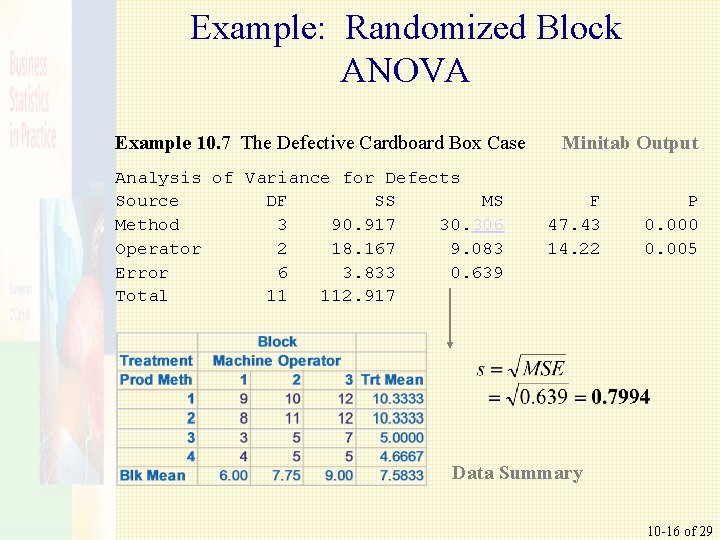
Example: Randomized Block Design Example 10. 7 The Defective Cardboard Box Case 10 -12 of 29

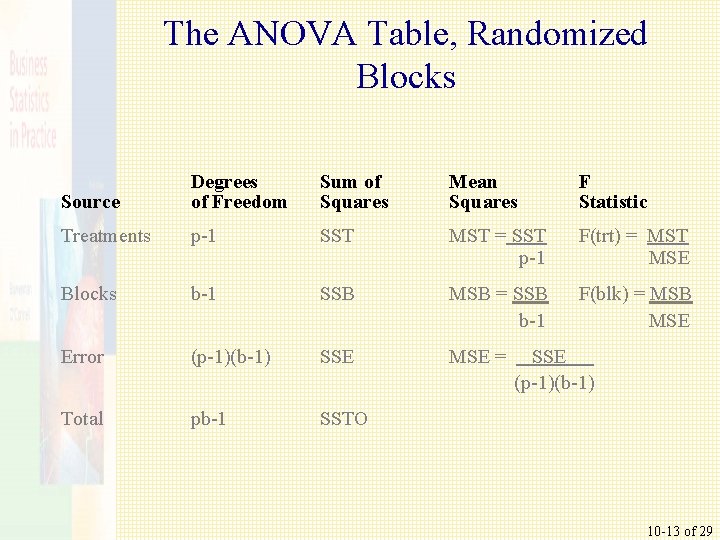
The ANOVA Table, Randomized Blocks Source Degrees of Freedom Sum of Squares Mean Squares F Statistic Treatments p-1 SST MST = SST p-1 F(trt) = MST MSE Blocks b-1 SSB MSB = SSB b-1 F(blk) = MSB MSE Error (p-1)(b-1) SSE MSE = Total pb-1 SSTO SSE (p-1)(b-1) 10 -13 of 29

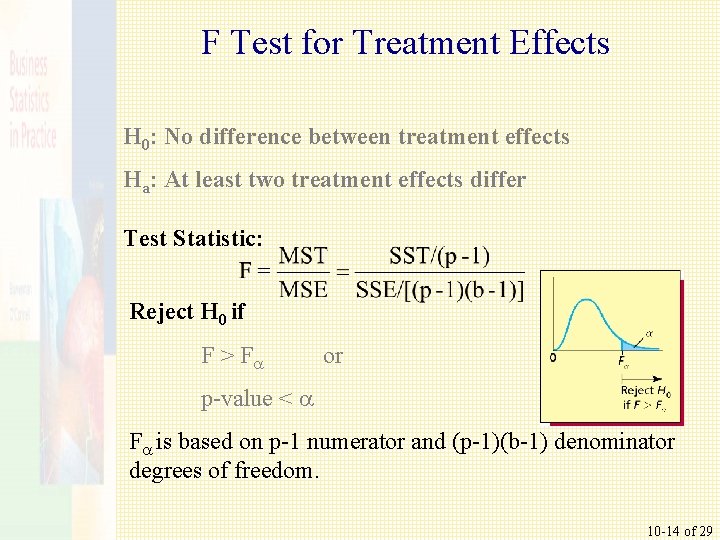
F Test for Treatment Effects H 0: No difference between treatment effects Ha: At least two treatment effects differ Test Statistic: Reject H 0 if F > F or p-value < F is based on p-1 numerator and (p-1)(b-1) denominator degrees of freedom. 10 -14 of 29

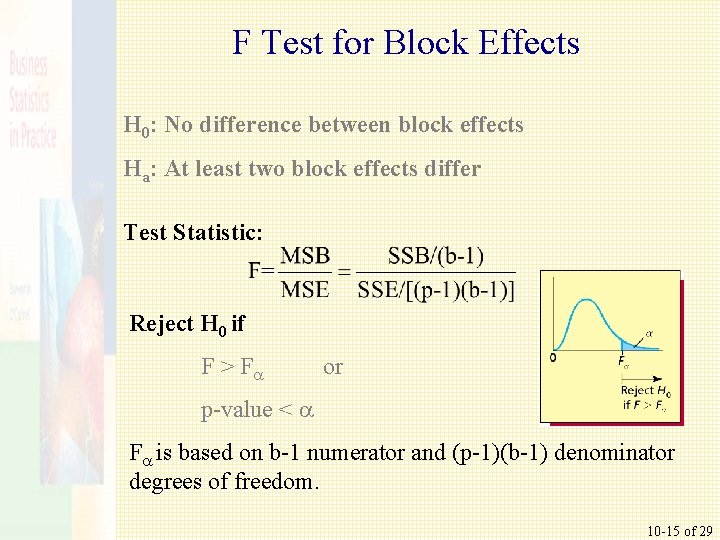
F Test for Block Effects H 0: No difference between block effects Ha: At least two block effects differ Test Statistic: Reject H 0 if F > F or p-value < F is based on b-1 numerator and (p-1)(b-1) denominator degrees of freedom. 10 -15 of 29

Example: Randomized Block ANOVA Example 10. 7 The Defective Cardboard Box Case Analysis of Variance for Defects Source DF SS MS Method 3 90. 917 30. 306 Operator 2 18. 167 9. 083 Error 6 3. 833 0. 639 Total 11 112. 917 Minitab Output F 47. 43 14. 22 P 0. 000 0. 005 Data Summary 10 -16 of 29

Estimation of Treatment Differences Under Randomized Blocks, Individual Intervals Individual 100(1 - a)% confidence interval for mi - mh t /2 is based on (p-1)(b-1) degrees of freedom. Example 10. 8 The Defective Cardboard Box Case (4 vs 1) t. 025 with (3 -1)(4 -1) = 6 degrees of freedom. 10 -17 of 29

Estimation of Treatment Differences Under Randomized Blocks, Simultaneous Intervals Tukey simultaneous 100(1 - a)% confidence interval for mi - mh q is the upper percentage point of the studentized range for p and (p-1)(b-1) from Table A. 9. Example 10. 8 The Defective Cardboard Box Case (4 vs 1) q. 05 for 4 and 6. 10 -18 of 29

10. 4 Two-Way Analysis of Variance A two factorial design compares the mean response for a levels of factor 1 (for example, display height) and each of b levels of factor 2 ( for example, display width. ) A treatment is a combination of a level of factor 1 and a level of factor 2. Factor 1 1 1 2. . . a Factor 2 2 3… b xijk = response for the kth experimental unit (k=1, …, m) assigned to the ith level of Factor 1 and the jth level of Factor 2 10 -19 of 29

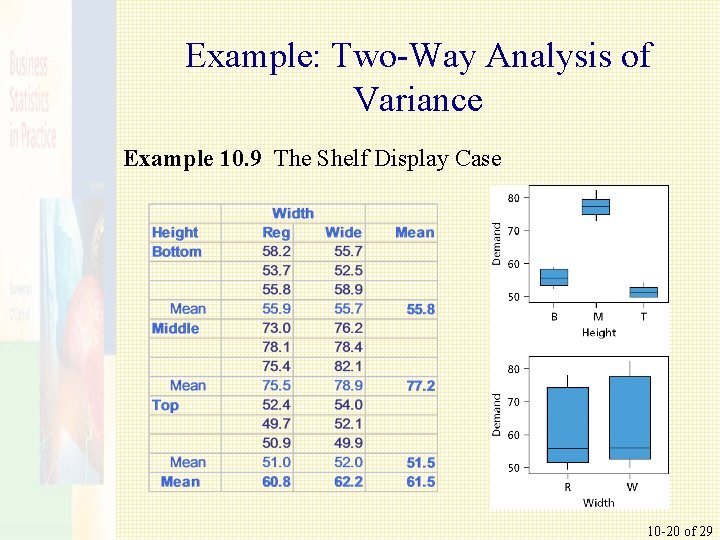
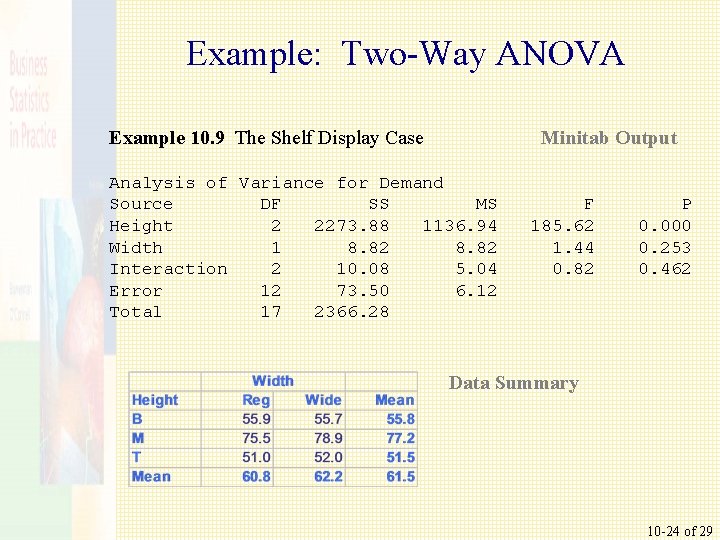
Example: Two-Way Analysis of Variance Example 10. 9 The Shelf Display Case 10 -20 of 29

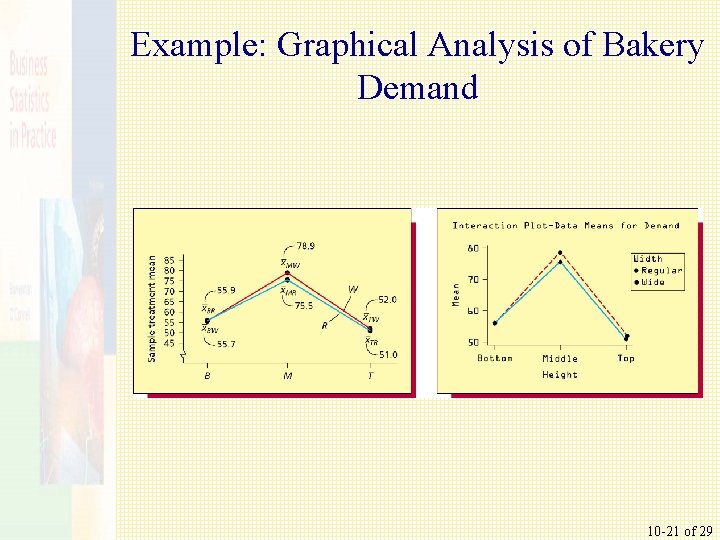
Example: Graphical Analysis of Bakery Demand 10 -21 of 29

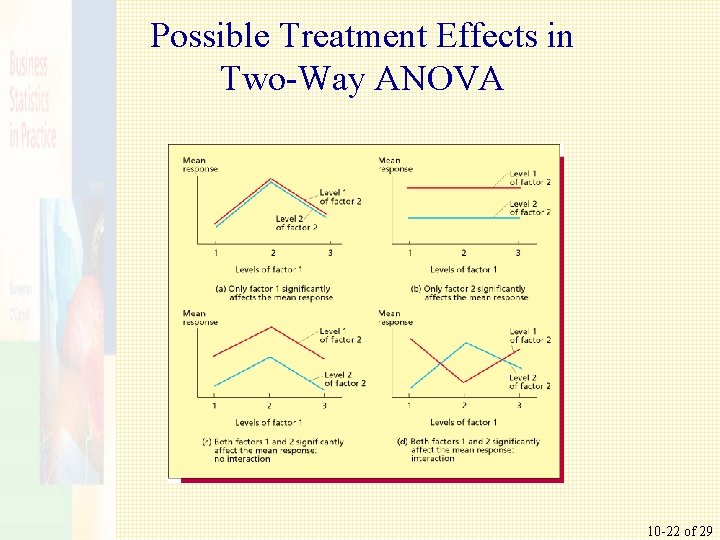
Possible Treatment Effects in Two-Way ANOVA 10 -22 of 29

Two-Way ANOVA Table Source Degrees of Freedom Sum of Squares Mean Squares F Statistic Factor 1 a-1 SS(1) MS(1) = SS(1) a-1 F(1) = MS(1) MSE Factor 1 b-1 SS(2) MS(2) = SS(2) b-1 F(2) = MS(2) MSE Interaction (a-1)(b-1) SS(int) MS(int) = SS(int) F(int) = MS(int) (a-1)(b-1) MSE Error ab(m-1) SSE MSE = Total abm-1 SSTO SSE ab(m-1) 10 -23 of 29

Example: Two-Way ANOVA Example 10. 9 The Shelf Display Case Minitab Output Analysis of Variance for Demand Source DF SS MS Height 2 2273. 88 1136. 94 Width 1 8. 82 Interaction 2 10. 08 5. 04 Error 12 73. 50 6. 12 Total 17 2366. 28 F 185. 62 1. 44 0. 82 P 0. 000 0. 253 0. 462 Data Summary 10 -24 of 29

F Tests for Treatment Effects H 0: No difference between treatment effects Ha: At least two treatment effects differ Test Statistics: Main Effects F is based on a-1 and ab(m-1) degrees of freedom. F is based on b-1 and ab(m-1) degrees of freedom. Interaction F is based on (a-1)(b-1) and ab(m-1) degrees of freedom. Reject H 0 if F > F or p-value < 10 -25 of 29

Estimation of Treatment Differences Under Two-Way ANOVA, Factor 1 Individual 100(1 - a)% confidence interval for mi - mi’ t /2 is based on ab(m-1) degrees of freedom. Tukey simultaneous 100(1 - a)% confidence interval for mi - mi’ q is the upper percentage point of the studentized range for a and ab(m-1) from Table A. 9. Example 10. 10 The Shelf Display Case (M vs B) 10 -26 of 29

Estimation of Treatment Differences Under Two-Way ANOVA, Factor 2 Individual 100(1 - a)% confidence interval for m j - m j’ t /2 is based on ab(m-1) degrees of freedom. Tukey simultaneous 100(1 - a)% confidence interval for m j - m j’ q is the upper percentage point of the studentized range for b and ab(m-1) from Table A. 9. 10 -27 of 29

Experimental Design and Analysis of Variance 10. 1 Basic Concepts of Experimental Design Summary: 10. 2 One-Way Analysis of Variance 10. 3 The Randomized Block Design 10. 4 Two-Way Analysis of Variance 10 -28 of 29
 Analysis of variance
Analysis of variance Non experimental design vs experimental
Non experimental design vs experimental Perbedaan one way dan two way anova
Perbedaan one way dan two way anova One way anova vs two way anova
One way anova vs two way anova Two way anova adalah
Two way anova adalah Rsq in standard costing
Rsq in standard costing Experimental vs non experimental
Experimental vs non experimental What is quasi experimental research
What is quasi experimental research Disadvantages of experimental research
Disadvantages of experimental research Experimental vs non experimental
Experimental vs non experimental How to linearize a top opening parabola
How to linearize a top opening parabola How to make a flexible budget
How to make a flexible budget Multivariate analysis of variance and covariance
Multivariate analysis of variance and covariance Standard cost vs budgeted cost
Standard cost vs budgeted cost Sales activity variance
Sales activity variance Analysis of variance and covariance
Analysis of variance and covariance Material price variance
Material price variance What is independent variable in science
What is independent variable in science Experimental design independent and dependent variables
Experimental design independent and dependent variables Statistics
Statistics Ethical issues in experimental research
Ethical issues in experimental research Experimental design questions and answers
Experimental design questions and answers Forms and reports in system analysis and design
Forms and reports in system analysis and design Mixed design anova spss
Mixed design anova spss Anova matrix form
Anova matrix form Contoh soal rancangan tersarang
Contoh soal rancangan tersarang Budget variance analysis
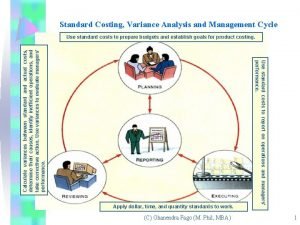
Budget variance analysis The variance analysis cycle:
The variance analysis cycle: Budget variance analysis
Budget variance analysis