Anlisis de Algoritmos Introduccin al anlisis de algoritmos

Análisis de Algoritmos Introducción al análisis de algoritmos

¿Qué es un algoritmo? n “(del árabe al-Khowârizmî, sobrenombre del célebre matemático árabe Mohámed ben Musa). Conjunto ordenado y finito de operaciones que permite encontrar la solución a un problema…” n Un algoritmo, puede expresarse en términos de un lenguaje de programación, para obtener un programa que resuelve el problema por medio de la computadora. 2

¿Cómo expresaremos los algoritmos en el curso? n Utilizando lenguaje natural: n Puede haber ambigüedades… n El grado de especificación es subjetivo… n Utilizando pseudocódigo en un lenguaje computacional: n n n No hay ambigüedades, pues se trabaja con estructuras de control: secuencia, decisiones, ciclos, recursividad. El grado de especificación es estándar, aunque el diseño puede variar. Facilidad de convertirlos en programas computacionales. 3

Cita. . . n “No hay un incremento concebible en el poder de las computadoras que pueda saturar la demanda científica: aún pensando que una computadora posea un ciclo de tiempo subnuclear (10 -23 seg. ) y densidades de almacenamiento subnucleares (1039 bits/cm 3), ésta no podría manejar la mayoría de los problemas que son importantes en la investigación científica básica y aplicada. Por lo tanto, existirá siempre una fuerte presión para incrementar la eficiencia de los programas, para poder incrementar también la cantidad de información últil generada por un programa. ” Ken Wilson, Nóbel de Física 1982 4

Áreas de estudio n ¿Cómo construir algoritmos? n Técnicas de diseño n ¿Cómo expresar algoritmos? n Enfoques de los lenguajes de programación n ¿Cómo validar algoritmos? n Verificación formal n ¿Cómo analizar algoritmos? n Complejidad computacional, eficiencia, legibilidad, usabilidad, etc. . . 5

Análisis de algoritmos n Si se tuvieran 2 programas que hacen lo mismo, ¿cómo se podrían comparar? 1. Eficiencia: Tiempo de ejecución n Uso de espacios de memoria n 2. Facilidad de lectura, mantenimiento, rapidez para codificarlo. 6

Medición del tiempo de ejecución n El tiempo de ejecución depende de: 1. La entrada al programa: Su tamaño Sus características 2. La calidad del código generado para el programa por el compilador. 3. La rapidez de las instrucciones de máquina. 4. La complejidad de tiempo del algoritmo. 7

¿Cómo medir? n Cantidad de instrucciones básicas (o elementales) que se ejecutan. n Ejemplos de instrucciones básicas: asignación de escalares n lectura o escritura de escalares n saltos (goto’s) implícitos o explícitos. n evaluación de condiciones n llamada a funciones n etc. n 8

Ejemplo cont = 1; while (cont <= n) do x = x + a[cont]; x = x + b[cont]; cont = cont + 1; à 1 àn+1 àn àn (goto implícito) à 1 goto en falso. TOTAL: 5 n + 3 9

Ejemplo z = 0; for x = 1 to n do for y = 1 to n do z = z + a[x, y]; à 1 asignación + (n+1) comparaciones à(n+2)*n = n 2 +2 n àn*n = n 2 à 2 n 2 (incremento + goto implícito) àn (goto en falso for y) à 2 n (incremento + goto implícito) à 1 (goto en falso for x) TOTAL: 4 n 2 + 6 n + 4 10

Consecuencia… n Se requiere contar con una notación que permita comparar la eficiencia entre los algoritmos… n La NOTACIÓN ASINTÓTICA es la propuesta de notación aceptada por la comunidad científica para describir el comportamiento en eficiencia (o complejidad) de un algoritmo. n Describe en forma sintética el comportamiento de la función que con la variable de entrada, determina el número de operaciones que realiza el algoritmo. 11

NOTACIÓN ASINTÓTICA n COMPLEJIDAD TEMPORAL (y ESPACIAL). Tiempo (o espacio) requerido por un algoritmo, expresado en base a una función que depende del tamaño del problema. n COMPLEJIDAD TEMPORAL ASINTÓTICA (y ESPACIAL). Comportamiento límite conforme el tamaño del problema se incrementa. Determina el tamaño del problema que puede ser resuelto por un algoritmo. 12

Definición n Se dice que la función f(n) “es de orden g(n)” [O(g(n))], O(g(n)) si existen constantes positivas c y n 0 tales que f(n) <= c g(n) cuando n >= n 0 n Ejemplos: n n+5 es O(n) pues n+5 <= 2 n para toda n >= 5 n (n+1)2 es O(n 2) pues (n+1)2 <= 4 n 2 para n>= 1 n (n+1)2 NO es O(n) pues para cualquier c > 1 no se cumple que (n+1)2 <= c*n 13

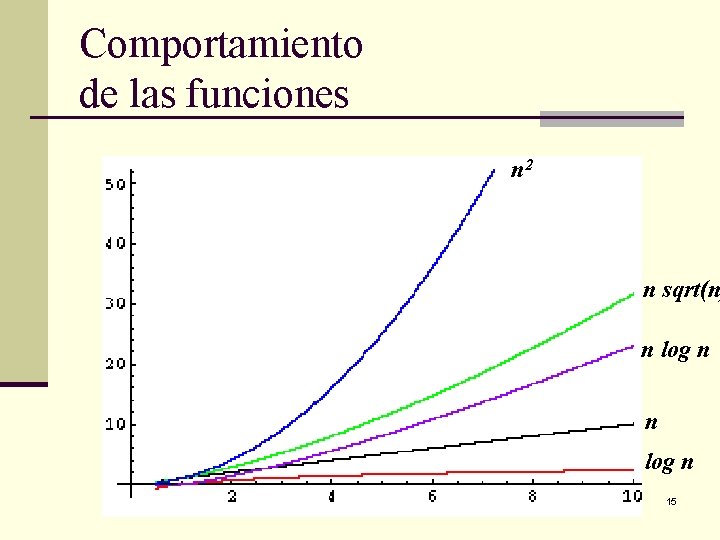
Ordenes más comunes de los algoritmos n O(1) n O(n 2 ) n O(n 3 ) n O (nm ) n O(log(n)) n O(nlog(n)) n O(mn ) n O(n!) Constante Lineal Cuadrático Cúbico Polinomial Logarítmico nlog (n) exponencial factorial 14

Comportamiento de las funciones n 2 n sqrt(n n log n 15

Ejemplo del comportamiento n Considerar que el algoritmo A 1 es de orden O(n log n) y que procesa 1, 000 datos en 1 segundo. n Su comportamiento al aumentar el tamaño de la entrada sería el siguiente: n = 2, 000 2. 2 segundos n = 5, 000 6. 2 segundos n = 10, 000 13. 3 segundos n = 100, 000 2. 77 minutos n = 1, 000 33. 3 minutos n = 10, 000 6. 48 horas 16

Ejemplo del comportamiento n Considerar que el algoritmo A 2 es de orden O(n 2) y que procesa 1, 000 datos en 1 segundo. n Su comportamiento al aumentar el tamaño de la entrada sería el siguiente: n = 2, 000 4 segundos n = 5, 000 25 segundos n = 10, 000 1. 66 minutos n = 100, 000 2. 77 horas n = 1, 000 11. 5 días n = 10, 000 3. 25 años 17

Ejemplo del comportamiento n Si se contara con un algoritmo A 3 de orden exponencial y que procesa 1, 000 datos en 1 segundo… n Su comportamiento al aumentar el tamaño de la entrada sería el siguiente: n = 1, 500 n = 2, 000 n = 2, 500 n = 3, 000 n = 3, 500 n = 5, 000 n = 10, 000 32 segundos 17. 1 minutos 9. 1 horas 12. 1 días 1. 09 años 35, 700 años 4. 02 X 1019 años !!! 18

¿Cómo afecta la velocidad de la computadora? n Ejemplo: Suponer que se tienen los siguientes algoritmos con la complejidad de tiempo correspondiente: A 1 con T(n) = 100 n A 2 con T(n) = 5 n 2 A 3 con T(n) = n 3/2 A 4 con T(n) = 2 n n ¿Cuál es el orden de cada algoritmo? 19

¿Cómo afecta la velocidad de la computadora? n También suponer que se dispone de 1, 000 segundos (aprox. 17 minutos) para ejecutar cada algoritmo… n ¿Cuál es el tamaño máximo de la entrada que se puede procesar? A 1 con T(n) = 100 n A 2 con T(n) = 5 n 2 A 3 con T(n) = n 3/2 A 4 con T(n) = 2 n 10 14 12 10 20

¿Cómo afecta la velocidad de la computadora? n Suponer ahora que se cuenta con una computadora 10 veces más rápida… por lo tanto, es posible dedicar 10, 000 segundos a la solución de problemas que antes se les dedicaba 1, 000 segundos. . . n ¿Cuál es el tamaño máximo de la entrada que se puede procesar? A 1 con T(n) = 100 n A 2 con T(n) = 5 n 2 A 3 con T(n) = n 3/2 A 4 con T(n) = 2 n 100 45 27 13 21

¿Cómo afecta la velocidad de la computadora? n ¿Cuál fue el aumento en la capacidad de procesamiento de cada algoritmo con el incremento de 10 veces en la velocidad de la computadora? n ¿Cuál es el tamaño máximo de la entrada que se puede procesar? A 1 con T(n) = 100 n A 2 con T(n) = 5 n 2 A 3 con T(n) = n 3/2 A 4 con T(n) = 2 n 10 --> 100 14 --> 45 12 --> 27 10 --> 13 10 3. 2 2. 3 1. 3 22

Ejemplo: ¿Influye la computadora? n Para una Cray-1 utilizando Fortran, un algoritmo se procesa en 3 n 3 nanosegundos… Para n = 10, se tardaría 3 microsegundos… n Para n = 100, se tardaría 3 milisegundos… n Para n = 1, 000, se tardaría 3 segundos… n Para n = 2, 500, se tardaría 50 segundos… n Para n = 10, 000, se tardaría 49 minutos… n Para n = 1, 000, se tardaría 95 años!! n 23

Ejemplo: ¿Influye la computadora? n Para una TRS-80 (computadora personal Tandy de los 80’s) utilizando Basic, un algoritmo se procesa en 19, 500, 000 n nanosegundos… Para n = 10, se tardaría. 2 segundos… n Para n = 100, se tardaría 2 segundos… n Para n = 1, 000, se tardaría 20 segundos… n Para n = 2, 500, se tardaría 50 segundos… n Para n = 10, 000, se tardaría 3. 2 minutos… n Para n = 1, 000, se tardaría 5. 4 horas. . . n 24

Diseño de algoritmos: viéndolo en acción n Encontrar el n-ésimo elemento de la serie de Fibonacci…. n Algoritmos de solución: Iterativo (técnica de la programación dinámica). n Recursivo (técnica de “divide y vencerás”). n n Complejidad de los algoritmos (análisis): n Iterativo: O(n) n Recursivo: O(2 n/2) 25

Caso Fibonacci… n Supongamos una máquina que procese una operación básica en 1 nanosegundo… n Para encontrar el elemento #80 de la serie se tardarían: n n Iterativo. . . . : 81 nanosegundos. Recursivo. . : 18 minutos. n Para encontrar el elemento #121 se tardarían: n Iterativo. . . . : 121 nanosegundos. n Recursivo. . : 36 años!!!!. n ¿Importa el diseño del algoritmo? 26

Algoritmo Fibonacci #include <iostream. h> long int fibo 1 (int n) { long int ant = 1, act = 1, aux; for (int i=3; i <= n; i++) { aux = ant + act; ant = act; act = aux; } return act; } long int fibo 2 (int n) { if (n <3) return 1; else return (fibo 2(n-1) + fibo 2(n-2)); } Iterativo Recursivo main() { int n; do { cout << "Dame el valor de n: "; cin >> n; cout << "El n-esimo numero de la serie de Fibonacci es: " << fibo 1(n) << endl; } while (n>1); } 27

Conclusión n “A medida de que los computadores aumenten su rapidez y disminuyan su precio, como con toda seguiridad seguirá sucediendo, también el deseo de resolver problemas más grandes y complejos seguirá creciendo. Así la importancia del descubrimiento y el empleo de algoritmos eficientes irá en aumento, en lugar de disminuir. . . ” Aho, Hopcroft, Ullman, 1983 28

Por lo tanto. . . n Es importante aprender a analizar algoritmos… n Es importante conocer técnicas para diseñar algoritmos eficientes… n Y así, ante un problema, tener capacidad de decidir y aplicar el mejor algoritmo de solución. . . 29

En resumen. . . n ¿Cómo analizar la complejidad de tiempo de un algoritmo? n Contando la cantidad de operaciones básicas n n Las que más se repiten Convirtiendo a Notación Asintótica n Tomando el término más representativo 30

Ejemplo: Sumar los datos de un arreglo suma = 0; for i = 1 to n do suma = suma + arreglo[ i ]; ¿Cómo obtener la complejidad de tiempo del algoritmo? n Operación básica: suma = suma + arreglo[ i ] ; n Se realiza n veces n Algoritmo de orden n: O(n) 31

Otro método para calcular la complejidad n Consiste en aplicar reglas a los estatutos estructurados: 1. Secuencia de instrucciones 2. Decisiones (ejemplo: if) 3. Ciclos (ejemplo: while) 4. Recursividad 32

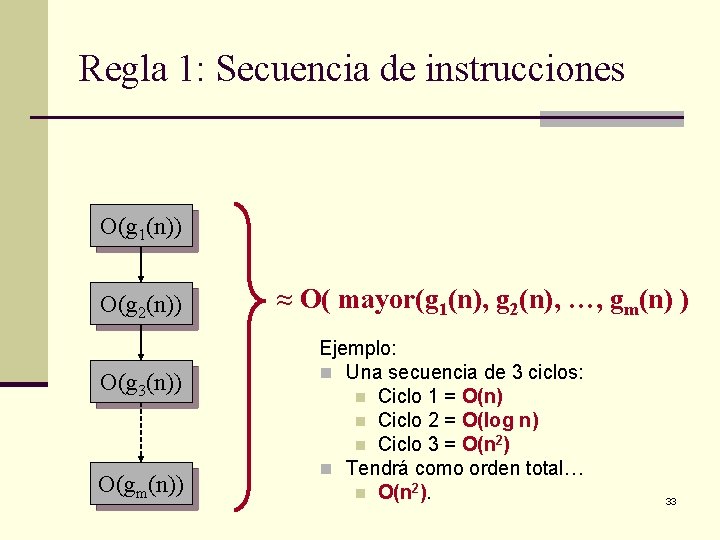
Regla 1: Secuencia de instrucciones O(g 1(n)) O(g 2(n)) O(g 3(n)) O(gm(n)) ≈ O( mayor(g 1(n), g 2(n), …, gm(n) ) Ejemplo: n Una secuencia de 3 ciclos: n Ciclo 1 = O(n) n Ciclo 2 = O(log n) n Ciclo 3 = O(n 2) n Tendrá como orden total… n O(n 2). 33

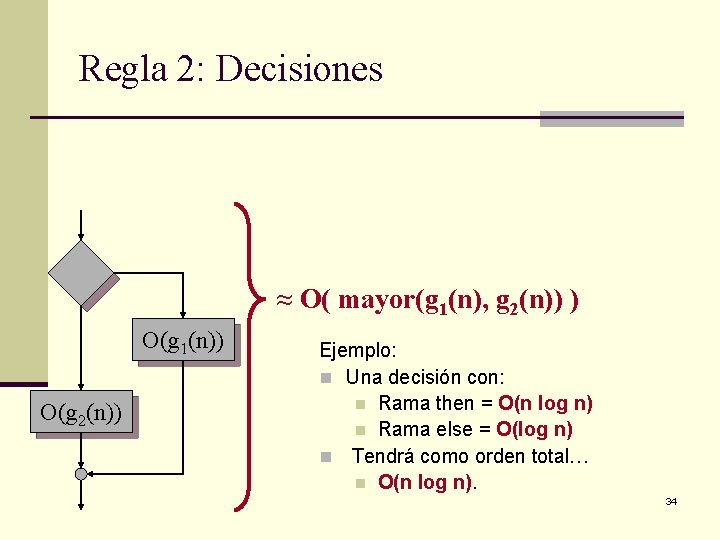
Regla 2: Decisiones ≈ O( mayor(g 1(n), g 2(n)) ) O(g 1(n)) O(g 2(n)) Ejemplo: n Una decisión con: n Rama then = O(n log n) n Rama else = O(log n) n Tendrá como orden total… n O(n log n). 34

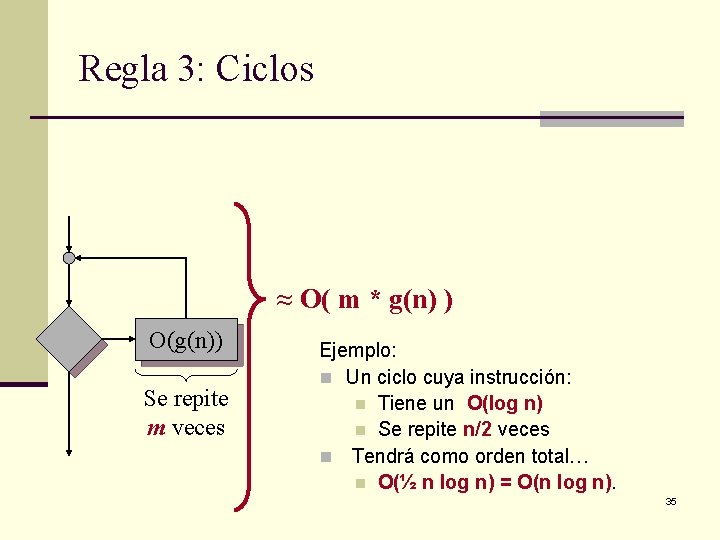
Regla 3: Ciclos ≈ O( m * g(n) ) O(g(n)) Se repite m veces Ejemplo: n Un ciclo cuya instrucción: n Tiene un O(log n) n Se repite n/2 veces n Tendrá como orden total… n O(½ n log n) = O(n log n). 35

Consideraciones especiales n En decisiones y ciclos anidados: n Analizar el código desde la instrucción más interna hacia el más externa. n Tip para los ciclos: n ¿“Normalmente” cuál es el orden de la instrucción interna? n n Si la variable de control se incrementa o decrementa con un valor constante: Orden LINEAL. Si la variable de control se multiplica o divide por un valor constante: Orden LOGARÍTIMICO. 36

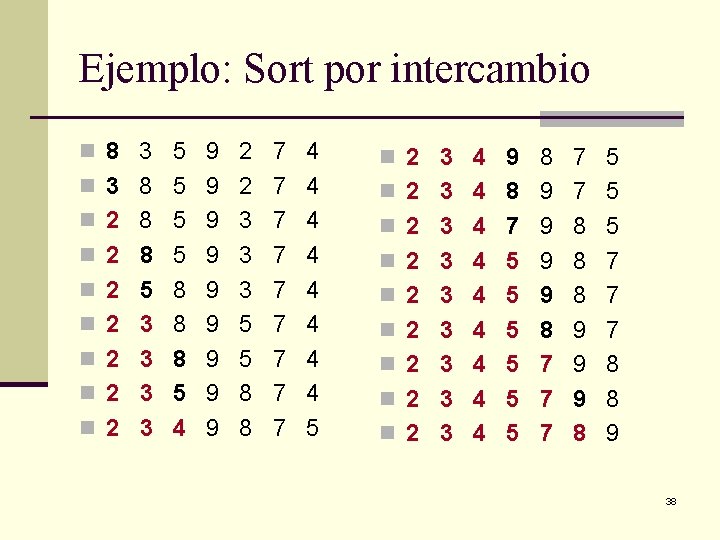
Ejemplo: Sort por intercambio n Toma la primera posición del arreglo, y compara su contenido contra el resto de los valores del arreglo. Cada vez que se encuentra un elemento menor al de la posición, lo intercambia. Esto asegura que el dato queda en la primera posición está ordenado. n El proceso se repite con la segunda posición, la tercera y así sucesivamente hasta la penúltima posición, siempre comparando solamente contra los elementos desordenados. 37

Ejemplo: Sort por intercambio n 8 3 5 9 2 7 4 n 2 3 4 9 8 7 5 n 3 8 5 9 2 7 4 n 2 3 4 8 9 7 5 n 2 8 5 9 3 7 4 n 2 3 4 7 9 8 5 n 2 8 5 9 3 7 4 n 2 3 4 5 9 8 7 n 2 5 8 9 3 7 4 n 2 3 4 5 9 8 7 n 2 3 8 9 5 7 4 n 2 3 4 5 8 9 7 n 2 3 8 9 5 7 4 n 2 3 4 5 7 9 8 n 2 3 5 9 8 7 4 n 2 3 4 5 7 9 8 n 2 3 4 9 8 7 5 n 2 3 4 5 7 8 9 38

Ejemplo: Sort por intercambio for i = 1 to n-1 do for j = i+1 to n do if a[ j ] < a[ i ] then intercambia(a[ i ], a[ j ]); → O( 1 ) Regla 2: Decisiones = mayor de las 2 ramas 39

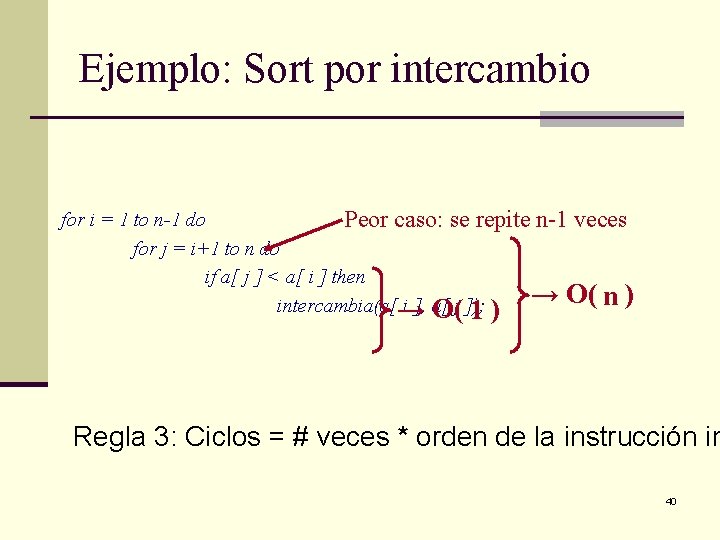
Ejemplo: Sort por intercambio for i = 1 to n-1 do Peor caso: se repite n-1 veces for j = i+1 to n do if a[ j ] < a[ i ] then → O( n ) intercambia(a[→ i ], a[ j ]); O( 1 ) Regla 3: Ciclos = # veces * orden de la instrucción in 40

Ejemplo: Sort por intercambio Se repite n-1 veces for i = 1 to n-1 do for j = i+1 to n do if a[ j ] < a[ i ] then O(j ]); n ) intercambia(a[ → i ], a[ → O( n 2 ) Regla 3: Ciclos = # veces * orden de la instrucción in 41

Ejemplo: Multiplicación de matrices a 11 a 12 … a 1 n a 21 a 22 … a 2 n … … b 11 b 12 … b 1 m X b 21 b 22 … b 2 m … am 1 am 2 … amn c 11 c 12 … c 1 m c 21 c 22 … c 2 m … … cm 1 cm 2 … cmm … … … = bn 1 bn 2 … bnm c 11 = a 11*b 11+a 12 *b 21 +…+ a 1 n *bn 1 c 12 = a 11*b 12+a 12 *b 22 +…+ a 1 n *bn 2 … c 21 = a 21*b 11+a 22 *b 21 +…+ a 2 n *bn 1 … cmm = am 1*b 1 m+am 2 *b 2 m +…+ amn *bnm cij = n aikbkj k=1 42

Ejemplo: Multiplicación de matrices O( n 3 ) ← for i = 1 to n do O( n 2 ) ← for j = 1 to n do O( 1 ) ← C[i, j] = 0; O( n ) ← for k = 1 to n do O( 1 ) ← C[i, j] = C[i, j] + A[i, k]*B[k, j]; 43

Regla 4: Recursividad n La complejidad de tiempo se obtiene contando la cantidad de veces que se hace la llamada recursiva. n Casos que “normalmente” se dan: n n n Orden LINEAL si sólo se tiene una llamada recursiva, con incrementos o decrementos en el parámetro de control. Orden LOGARITMICO si sólo se tiene una llamada recursiva, con multiplicaciones o divisiones en el parámetro de control. Si hay más de una llamada recursiva, el orden puede tender a ser EXPONENCIAL. 44

Ejemplo: Fibonacci (Iterativo) ant = 1; act = 1; while (n>2){ aux = ant + act; ant = act; act = aux; n = n - 1; } write (act); --> 1 --> n-2 + 1 --> n-2 --> n-2+1 --> 1 T(n) = 6 n-7 Por lo tanto el orden del algoritmo es O(n) 45

Ejemplo: Fibonacci (recursivo) Function fibonacci (n: int): int; if (n < 3) return 1; else return fibonacci(n-1) + fibonacci(n-2); n ¿Cómo obtener la complejidad de tiempo del algoritmo? n Cantidad de llamadas recursivas: 2 en cada llamada. n Algoritmo de orden: O(2 n/2) 46

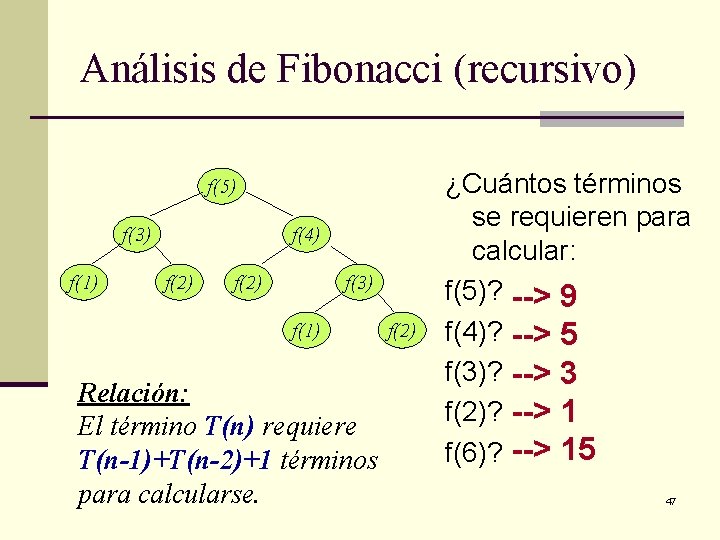
Análisis de Fibonacci (recursivo) f(5) f(3) f(1) f(4) f(2) f(3) f(1) Relación: El término T(n) requiere T(n-1)+T(n-2)+1 términos para calcularse. f(2) ¿Cuántos términos se requieren para calcular: f(5)? --> 9 f(4)? --> 5 f(3)? --> 3 f(2)? --> 1 f(6)? --> 15 47

Análisis de Fibonacci n Si el término T(n) requiere T(n-1)+T(n-2)+1 términos para calcularse… n se puede decir que T(n) > 2 * T(n-2) … n y por lo tanto: T(n) > 2 * T(n-4) … n y T(n) > 2 * 2 * T(n-6) … Por lo tanto: n y así sucesivamente hasta: T(n) > 2 n/2 y podemos decir T(n) > 2 * 2 * …. * 2 * T(1) que el orden del algoritmo es n/2 veces O(2 n/2) 48

Complejidades variables n Hasta ahora nuestro método funciona sin problemas si la complejidad es igual (constante) para cualquier contenido de la entrada. n Ejemplos: Sumar los elementos de un arreglo, Multiplicar 2 matrices, etc. n ¿Qué hacer si la complejidad varía dependiendo del contenido de la entrada? n Ejemplos: Búsqueda secuencial, binaria, etc. n Debemos utilizar: n La complejidad del algoritmo para el peor caso n En algunos algoritmos posibles, el caso promedio. 49

Ejemplo: Búsqueda secuencial pos = 1; while(pos<=n) and (arreglo[pos] < dato) do pos = pos + 1; if (pos > n) or (arreglo[pos]<>dato) then pos = 0; n Mejor caso: 1 Por lo tanto: n Peor caso: n O(n) n Caso promedio? n Depende de probabilidades: 3 n/4 + 1/4 50

Ejemplo: Búsqueda binaria inicio =1; fin = n; pos = 0; while (inicio<=fin) and (pos == 0) do mitad = (inicio+fin) div 2; if (x == arreglo[mitad]) then pos = mitad; else if (x < arreglo[mitad]) then fin = mitad-1 else inicio = mitad+1; n Operación Básica: x == arreglo[mitad] n Mejor caso: 1 51

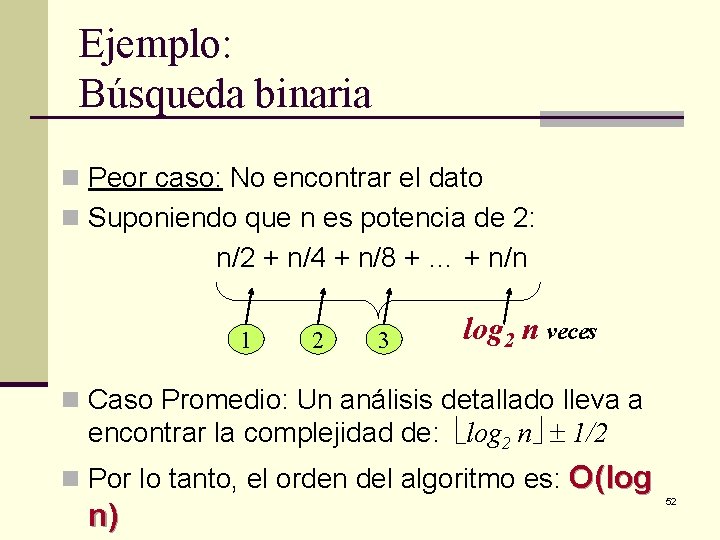
Ejemplo: Búsqueda binaria n Peor caso: No encontrar el dato n Suponiendo que n es potencia de 2: n/2 + n/4 + n/8 + … + n/n 1 2 3 log 2 n veces n Caso Promedio: Un análisis detallado lleva a encontrar la complejidad de: log 2 n 1/2 n Por lo tanto, el orden del algoritmo es: n) O(log 52

Ejercicios

Varios órdenes n Si un algoritmo tiene como función de complejidad la siguiente n T(n) = 3 n 0. 5 + 2 log(n 2) + 1000 n - 1/n n ¿Cuál es su órden? n O(n) 54

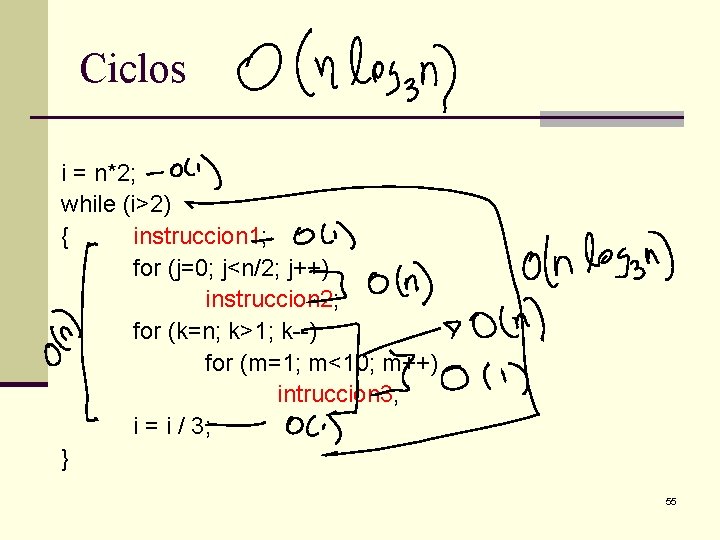
Ciclos i = n*2; while (i>2) { instruccion 1; for (j=0; j<n/2; j++) instruccion 2; for (k=n; k>1; k--) for (m=1; m<10; m++) intruccion 3; i = i / 3; } 55

Ciclos i = 1; while (i<n) { instruccion 1; for (j=1; j<n; j=j*2) { instruccion 2; for (k=n; k>1; k=k/3) intruccion 3; } i = i * 3; } 56

Búsqueda en un ABB nodo* buscar. Nodo (int numero, nodo* raiz) { if (raiz == NULL) return NULL; else if (numero == raiz->info) return raiz; else if (numero < raiz->info) return buscar. Nodo (numero, raiz->izq); else return buscar. Nodo (numero, raiz->der); } 58

Suma de Factoriales double factorial (num) { double fact=1; for (int i=1; i<=num; i++) fact = fact*i; return fact; } double suma. De. Factorial (limite) { double suma=1; for (int i = 1; i<=limite; i++) suma = suma + factorial(i); return suma; } 59