Anlise de Tendncia por Regresso EE240 Linear Anlise

Análise de Tendência por Regressão EE-240 Linear Análise de Tendência: Regressão Linear EE-240/2009

Análise de Tendência por Regressão Linear • Sir Francis Galton (1822 - 1911) Antropólogo e meteorologista britânico. • Regression towards mediocrity in hereditary stature. Journal of the Anthropological Institute, v. 15, pp. 246 -263, 1885. • A altura dos filhos tende a ser aproximar da média da população (“regressão à média”). • Atualmente, a palavra “regressão” não é mais empregada com esse sentido. EE-240/2009

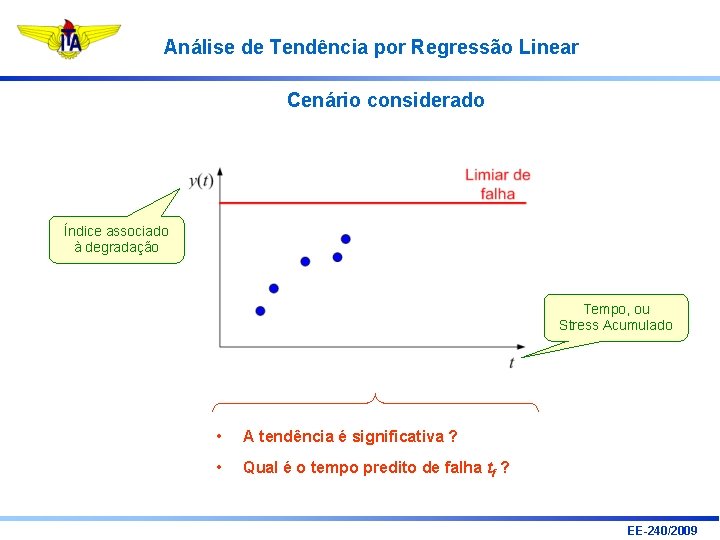
Análise de Tendência por Regressão Linear Cenário considerado Índice associado à degradação Tempo, ou Stress Acumulado • A tendência é significativa ? • Qual é o tempo predito de falha tf ? EE-240/2009

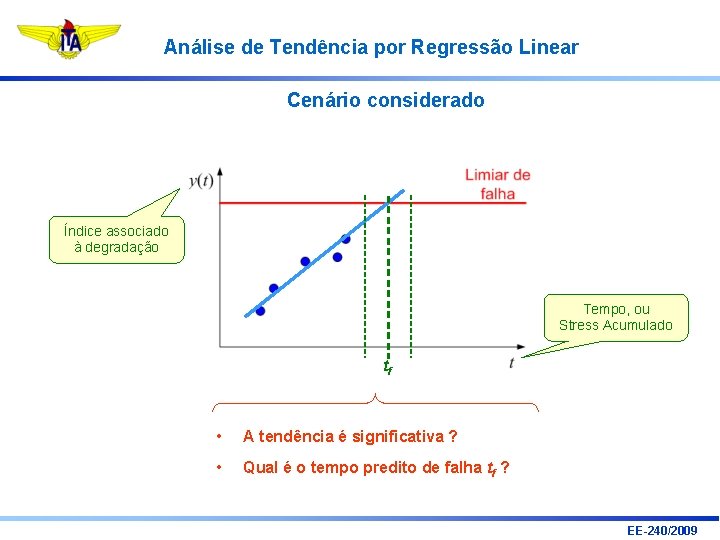
Análise de Tendência por Regressão Linear Cenário considerado Índice associado à degradação Tempo, ou Stress Acumulado • A tendência é significativa ? • Qual é o tempo predito de falha tf ? EE-240/2009

Análise de Tendência por Regressão Linear Cenário considerado Índice associado à degradação Tempo, ou Stress Acumulado tf • A tendência é significativa ? • Qual é o tempo predito de falha tf ? EE-240/2009

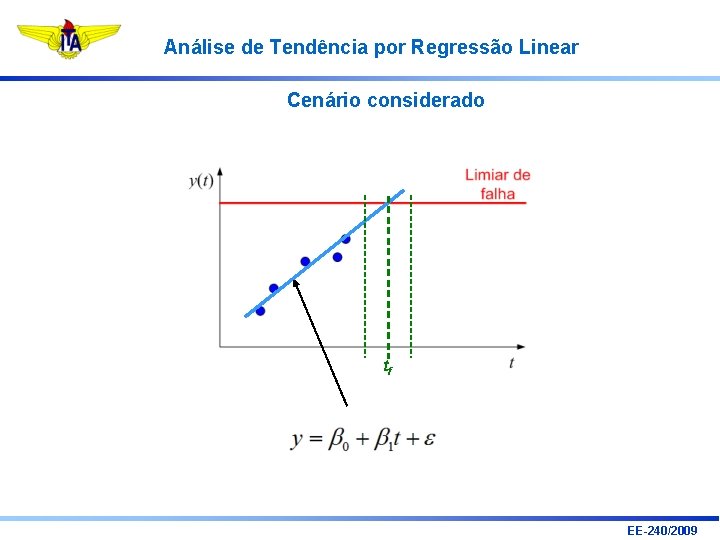
Análise de Tendência por Regressão Linear Cenário considerado tf EE-240/2009

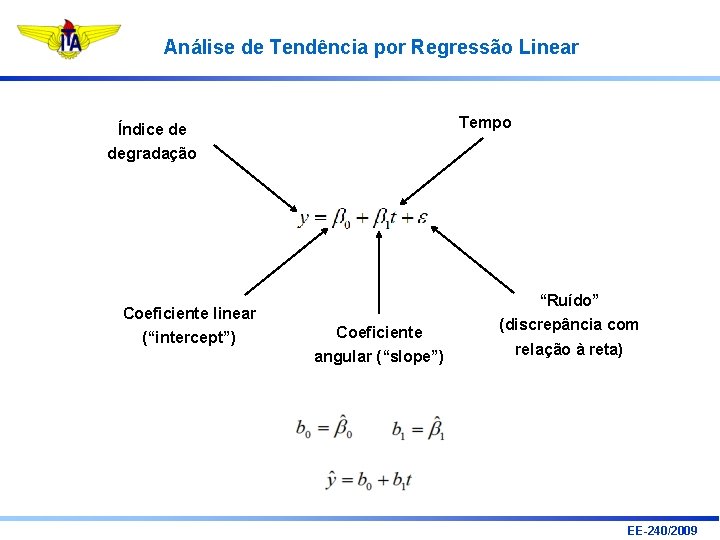
Análise de Tendência por Regressão Linear Tempo Índice de degradação Coeficiente linear (“intercept”) Coeficiente angular (“slope”) “Ruído” (discrepância com relação à reta) EE-240/2009

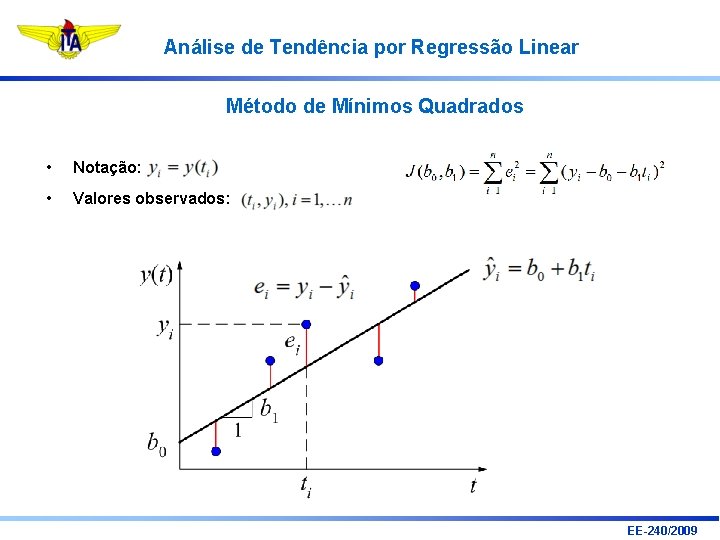
Análise de Tendência por Regressão Linear Método de Mínimos Quadrados • Notação: • Valores observados: EE-240/2009

Análise de Tendência por Regressão Linear EE-240/2009

Análise de Tendência por Regressão Linear • A reta ajustada passa no centróide do conjunto de pontos (ti, yi): • Os resíduos ei têm média zero: EE-240/2009

Análise de Tendência por Regressão Linear • Os resíduos não são correlacionados com o tempo: EE-240/2009

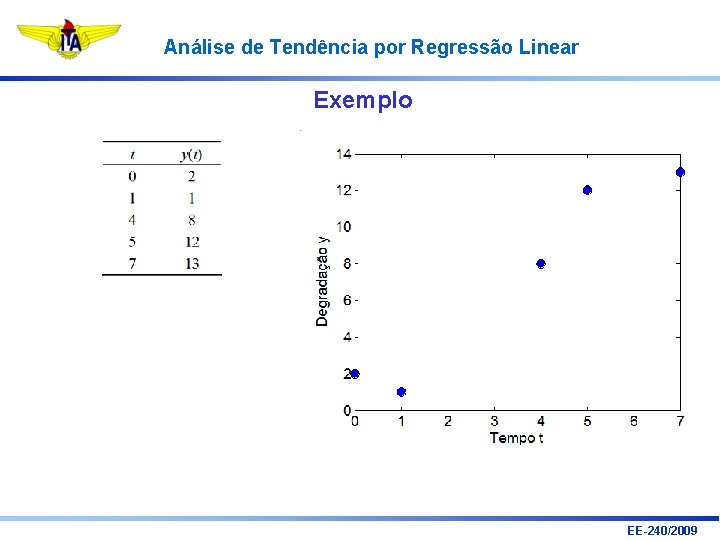
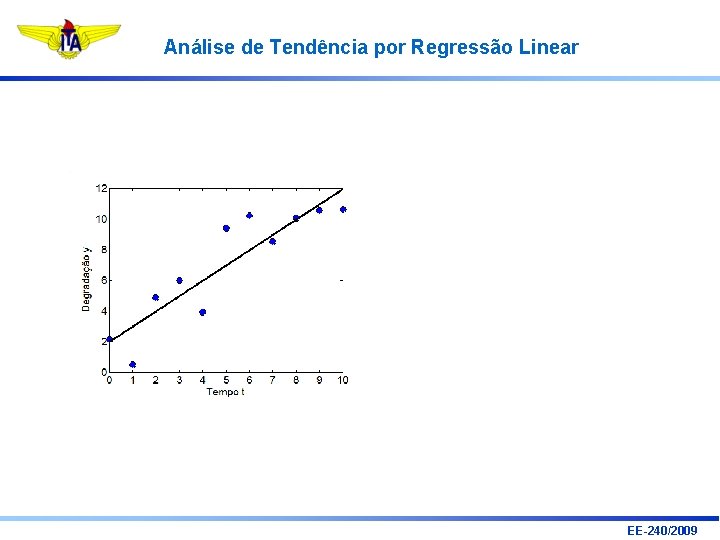
Análise de Tendência por Regressão Linear Exemplo EE-240/2009

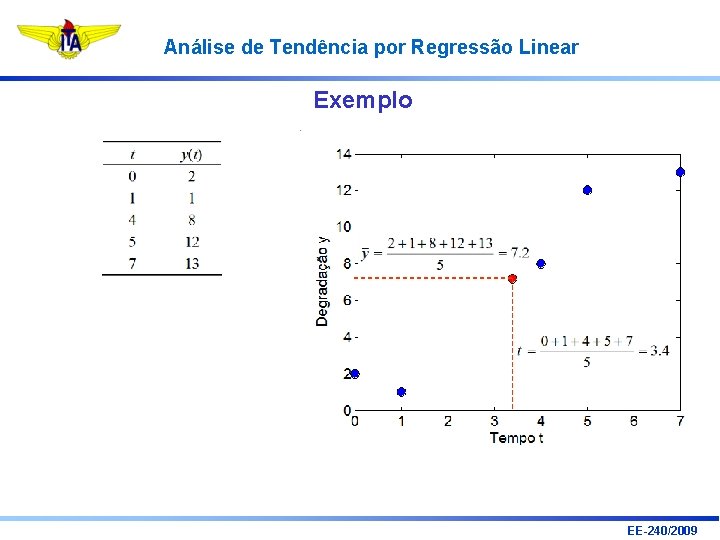
Análise de Tendência por Regressão Linear Exemplo EE-240/2009

Análise de Tendência por Regressão Linear Exemplo EE-240/2009

Análise de Tendência por Regressão Linear Exemplo REGRESS Multiple linear regression using least squares. b = REGRESS(y, X) returns the vector of regression coefficients, b, in the linear model y = Xb, (X is an nxp matrix, y is the nx 1 vector of observations). >> t = [0 1 4 5 7]' y = [2 1 8 12 13]' X = [ones(5, 1) t] b = regress(y, X) b = 0. 8916 1. 8554 EE-240/2009

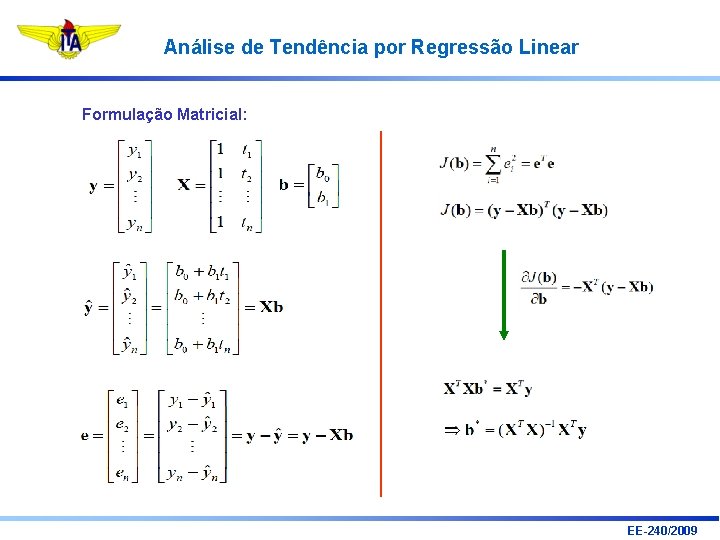
Análise de Tendência por Regressão Linear Formulação Matricial: EE-240/2009

Análise de Tendência por Regressão Linear >> t = [0 1 4 5 7]' >> y = [2 1 8 12 13]' >> X = [ones(5, 1) t] >> inv(X'*X)*X'*y ans = 0. 8916 1. 8554 EE-240/2009

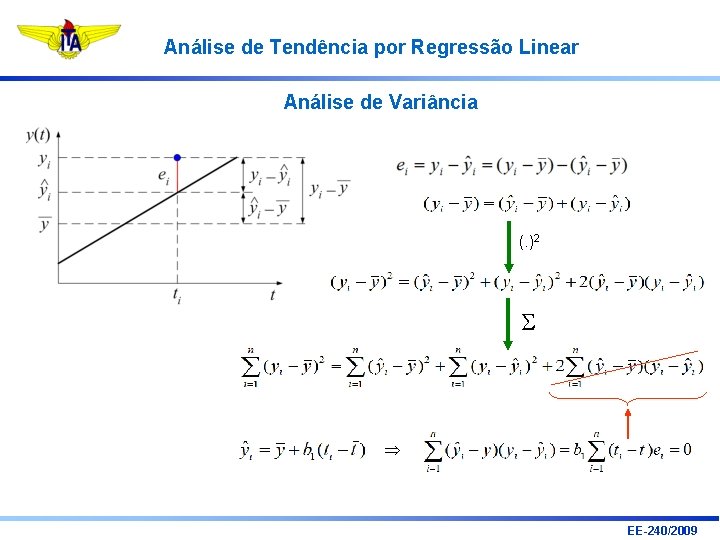
Análise de Tendência por Regressão Linear Análise de Variância (. )2 EE-240/2009

Análise de Tendência por Regressão Linear Dispersão dos valores de degradação observados Sum of squares about the mean SYY EE-240/2009

Análise de Tendência por Regressão Linear Dispersão associada ao aumento da degradação (tendência) Sum of squares due to regression SSReg EE-240/2009

Análise de Tendência por Regressão Linear Dispersão não explicada pelo modelo de tendência Sum of squares about regression (Residual Sum of Squares RSS) EE-240/2009

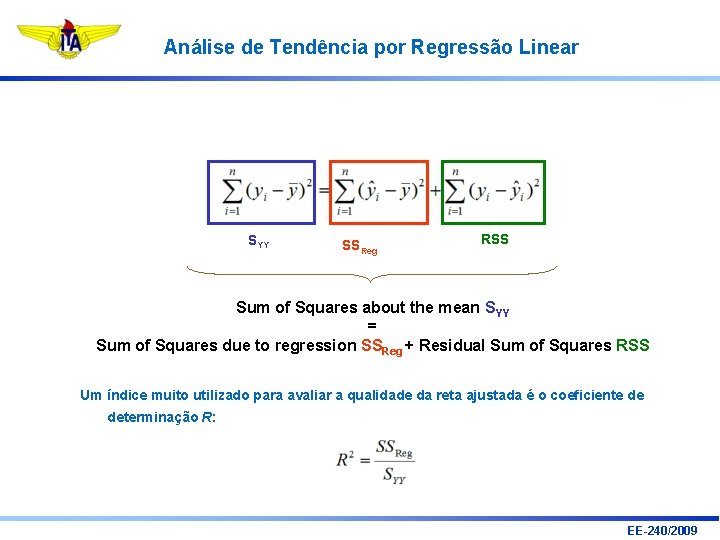
Análise de Tendência por Regressão Linear SYY SSReg RSS Sum of Squares about the mean SYY = Sum of Squares due to regression SSReg + Residual Sum of Squares RSS Um índice muito utilizado para avaliar a qualidade da reta ajustada é o coeficiente de determinação R: EE-240/2009

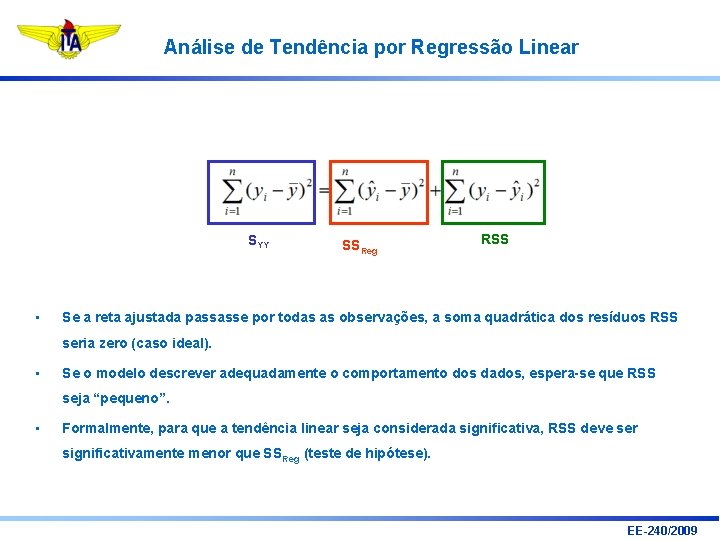
Análise de Tendência por Regressão Linear SYY • SSReg RSS Se a reta ajustada passasse por todas as observações, a soma quadrática dos resíduos RSS seria zero (caso ideal). • Se o modelo descrever adequadamente o comportamento dos dados, espera-se que RSS seja “pequeno”. • Formalmente, para que a tendência linear seja considerada significativa, RSS deve ser significativamente menor que SSReg (teste de hipótese). EE-240/2009

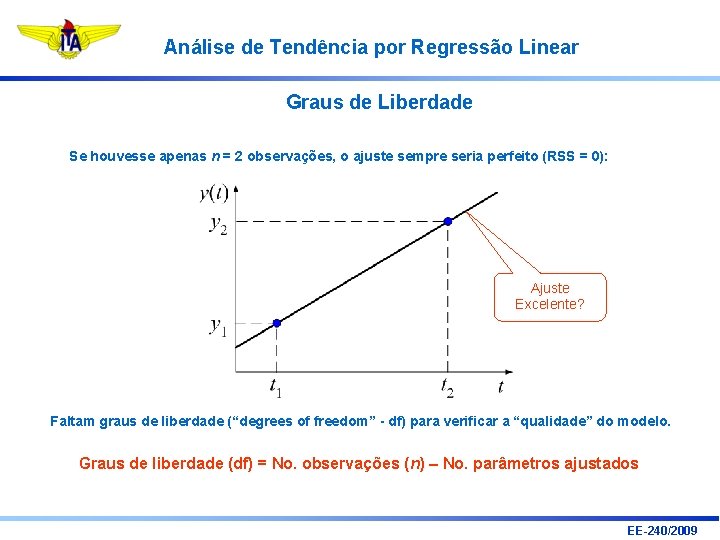
Análise de Tendência por Regressão Linear Graus de Liberdade Se houvesse apenas n = 2 observações, o ajuste sempre seria perfeito (RSS = 0): Ajuste Excelente? Faltam graus de liberdade (“degrees of freedom” - df) para verificar a “qualidade” do modelo. Graus de liberdade (df) = No. observações (n) – No. parâmetros ajustados EE-240/2009

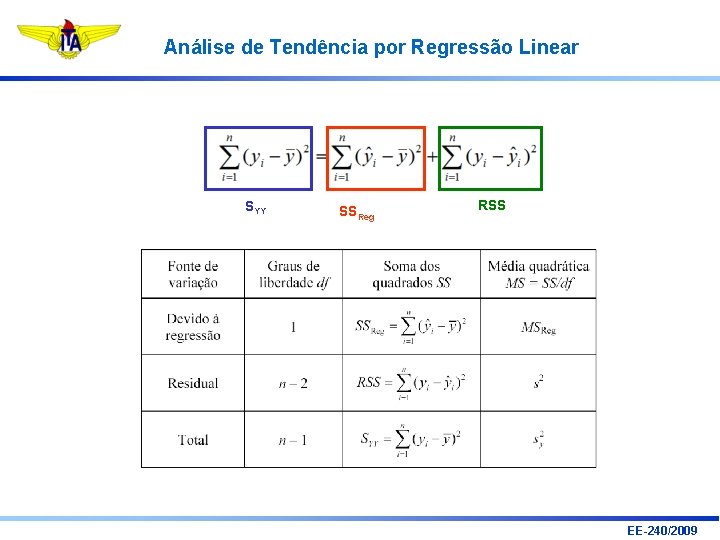
Análise de Tendência por Regressão Linear SYY • SSReg RSS Somas de quadrados devem ser comparadas levando-se em conta os graus de liberdade associados. • Para isso, podem-se usar médias quadráticas: Mean Square = Sum of Squares / Degrees of Freedom (MS = SS / df) EE-240/2009

Análise de Tendência por Regressão Linear SYY SSReg RSS EE-240/2009

Análise de Tendência por Regressão Linear • A significância da regressão (isto é, da tendência linear da degradação observada) pode ser avaliada comparando-se MSReg e s 2 EE-240/2009

Análise de Tendência por Regressão Linear Assumindo: ei ~ N(0, s 2) ei não correlacionado com ej (i j) Pode-se mostrar que: Se b 1 = 0 (i. e. se não houver tendência linear) a razão segue uma distribuição F com 1 e (n – 2) graus de liberdade: EE-240/2009

Análise de Tendência por Regressão Linear Teste F para Significância da Regressão • Hipótese nula H 0: b 1 = 0 (não há tendência linear) • Hipótese alternativa H 1: b 1 0 • Se F > Fcrit = F 1–a(1, n – 2), pode-se rejeitar a hipótese nula com 100 (1 – a) % de confiança. n = 11, a = 0. 2 Fcrit = 1. 91 Fcrit EE-240/2009

Análise de Tendência por Regressão Linear EE-240/2009

Análise de Tendência por Regressão Linear >> X = [ones(n, 1) t] >> b = inv(X'*X)*X'*y >> yhat = X*b >> ybar = mean(y) >> SYY = (y - ybar)'*(y-ybar) >> SSReg = (yhat -ybar)'*(yhat - ybar) >> R 2 = SSReg/SYY >> MSReg = SSReg >> RSS = (y - yhat)'*(y - yhat) >> s 2 = RSS/(n-2) >> F = MSReg/s 2 >> alpha = 0. 05 >> Fcrit = finv(1 -alpha, 1, n-2) >> p = 1 - fcdf(F, 1, n-2) EE-240/2009

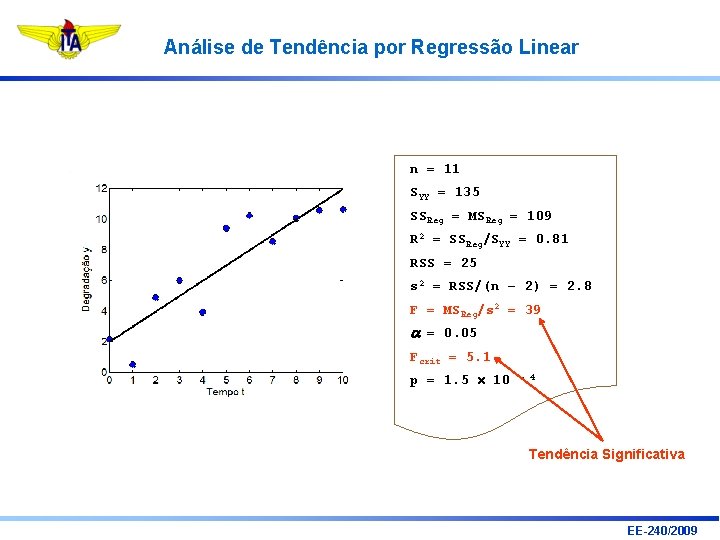
Análise de Tendência por Regressão Linear n = 11 SYY = 135 SSReg = MSReg = 109 R 2 = SSReg/SYY = 0. 81 RSS = 25 s 2 = RSS/(n – 2) = 2. 8 F = MSReg/s 2 = 39 a = 0. 05 Fcrit = 5. 1 p = 1. 5 10 - 4 Tendência Significativa EE-240/2009

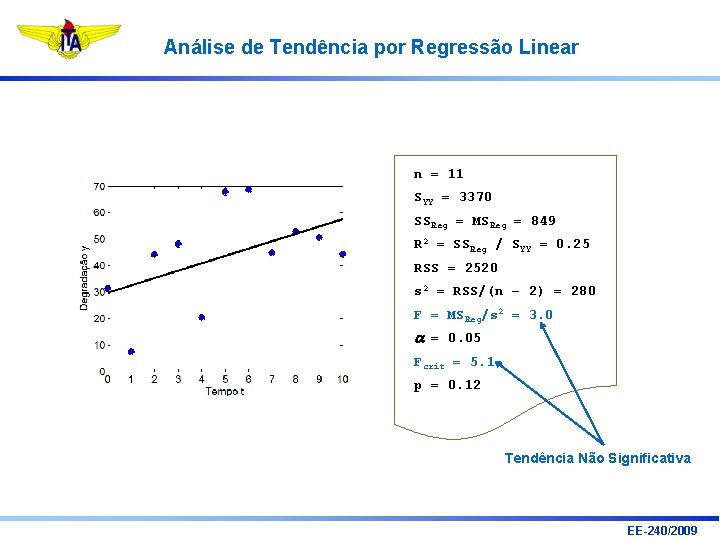
Análise de Tendência por Regressão Linear n = 11 SYY = 3370 SSReg = MSReg = 849 R 2 = SSReg / SYY = 0. 25 RSS = 2520 s 2 = RSS/(n – 2) = 280 F = MSReg/s 2 = 3. 0 a = 0. 05 Fcrit = 5. 1 p = 0. 12 Tendência Não Significativa EE-240/2009

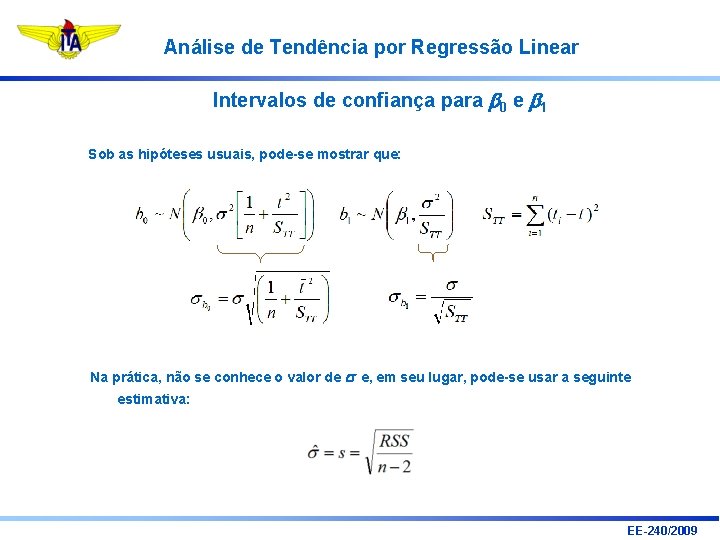
Análise de Tendência por Regressão Linear Intervalos de confiança para b 0 e b 1 Sob as hipóteses usuais, pode-se mostrar que: à Estimativas não-polarizadas à Variância aumenta com s 2 e diminui com n e STT ou seja, a precisão das estimativas melhora com: i) redução no “ruído” ii) aumento da quantidade de dados coletados iii) aumento no timespan da coleta de dados EE-240/2009

Análise de Tendência por Regressão Linear Intervalos de confiança para b 0 e b 1 Sob as hipóteses usuais, pode-se mostrar que: Na prática, não se conhece o valor de s e, em seu lugar, pode-se usar a seguinte estimativa: EE-240/2009

Análise de Tendência por Regressão Linear • Erro-padrão de b 0 e b 1: EE-240/2009

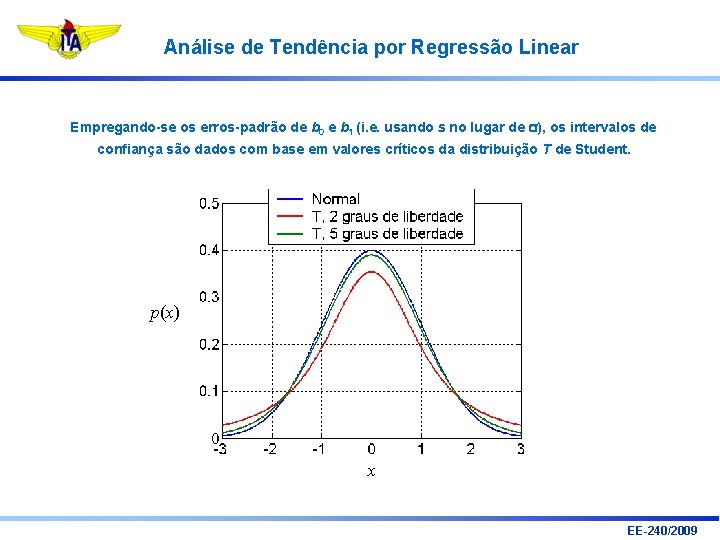
Análise de Tendência por Regressão Linear Empregando-se os erros-padrão de b 0 e b 1 (i. e. usando s no lugar de s), os intervalos de confiança são dados com base em valores críticos da distribuição T de Student. p(x) x EE-240/2009

Análise de Tendência por Regressão Linear Com 100 (1 – a) % de confiança, b 0 e b 1 encontram-se entre os seguintes limites: >> s = sqrt(s 2) >> tbar = mean(t) >> STT = (t - tbar)'*(t - tbar) >> sb 0 = s*sqrt(1/n + tbar^2/STT) >> sb 1 = s/sqrt(STT) >> Tcrit = tinv(1 -alpha/2, n-2) >> b 0_min = b 0 - sb 0*Tcrit >> b 0_max = b 0 + sb 0*Tcrit >> b 1_min = b 1 - sb 1*Tcrit >> b 1_max = b 1 + sb 1*Tcrit EE-240/2009

Análise de Tendência por Regressão Linear Exemplo b 0: [-0. 1562, 4. 1146] b 1: [0. 6369, 1. 3588] Valores usados para gerar este exemplo: b 0 = 3 b 1 = 0. 8 EE-240/2009

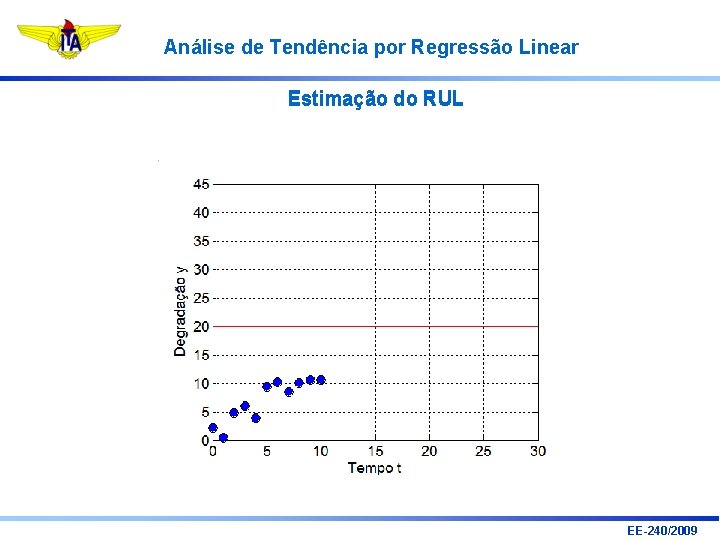
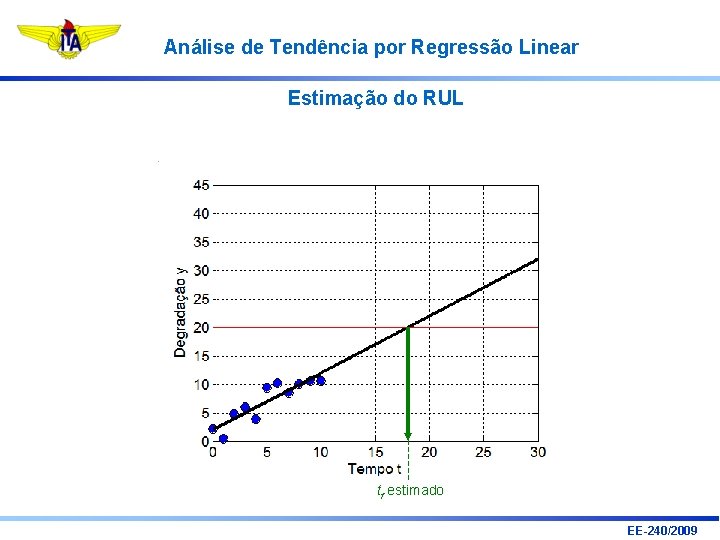
Análise de Tendência por Regressão Linear Estimação do RUL EE-240/2009

Análise de Tendência por Regressão Linear Estimação do RUL tf estimado EE-240/2009

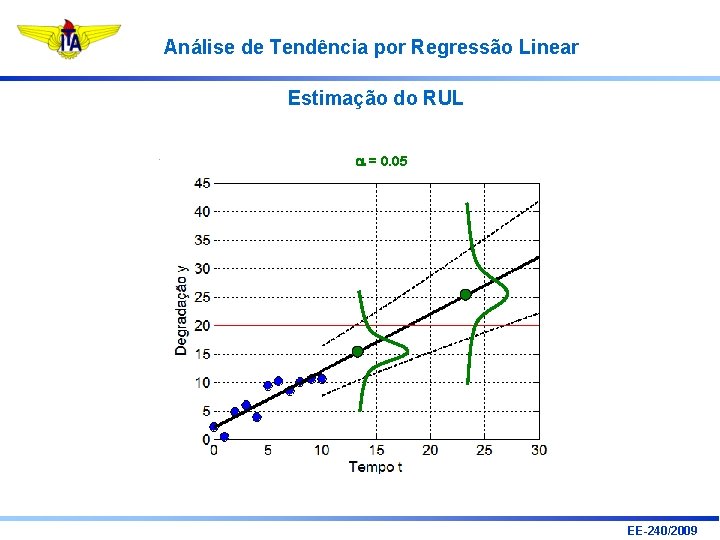
Análise de Tendência por Regressão Linear Estimação do RUL a = 0. 05 EE-240/2009

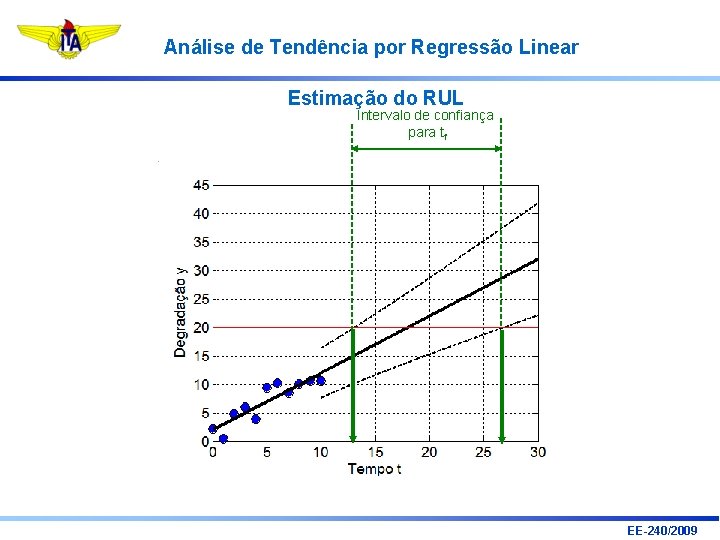
Análise de Tendência por Regressão Linear Estimação do RUL Intervalo de confiança para tf EE-240/2009

Análise de Tendência por Regressão Linear Muito Obrigado! EE-240/2009