Anlise de Regresso Anlise de Regresso um tipo











































- Slides: 54

Análise de Regressão

Análise de Regressão • É um tipo de análise que usa modelos matemáticos para relacionar o comportamento de uma variável Y com o de outra X. Ø Modelo Simples Y = f (X) Ø Modelo Multivariado Y = f (X 1, X 2, . . . Xn)

Análise de Regressão Para que serve saber a relação entre duas variáveis? • Para fazer PREVISÕES sobre o comportamento futuro de um fenômeno atual – extrapola-se para o futuro o comportamento presente das variáveis: - Ex: Prever a população de uma cidade no futuro. Prever a natalidade infantil para o ano 2050. Prever a demanda futura por habitação • Para SIMULAR os efeitos de uma variável X sobre uma variável Y. – avalia-se as relações de causa-efeito entre 2 variáveis - Ex: Simular os efeitos sobre a segurança na cidade (Y) em função do aumento do policiamento ostensivo nas ruas (X). Simular o efeito sobre o trânsito (Y) de uma cidade em função da elevação do preço da gasolina (X).

Análise de Regressão Os Modelos de Regressão aqueles que simulam o relacionamentos entre 2 ou mais variáveis. • O modelo é SIMPLES quando envolve o relacionamento entre duas variáveis. Esse relacionamento pode ser: • Simples Linear • Simples Não linear (equação da reta) ou, (equação exponencial, geométrica, . . . ) • O modelo é MULTIVARIADO quando envolve o relacionamento entre mais de duas variáveis: • Multivariado Linear (equação do plano) • Multivariado Não Linear

Análise de Regressão: Modelos A relação entre as variáveis é: § direta (ou positiva) quando os valores de Y aumentam em decorrência do aumento dos valores de X. Y Y X X § inversa (ou negativa) quando os valores de Y variam inversamente em relação aos de X. Y Y X X

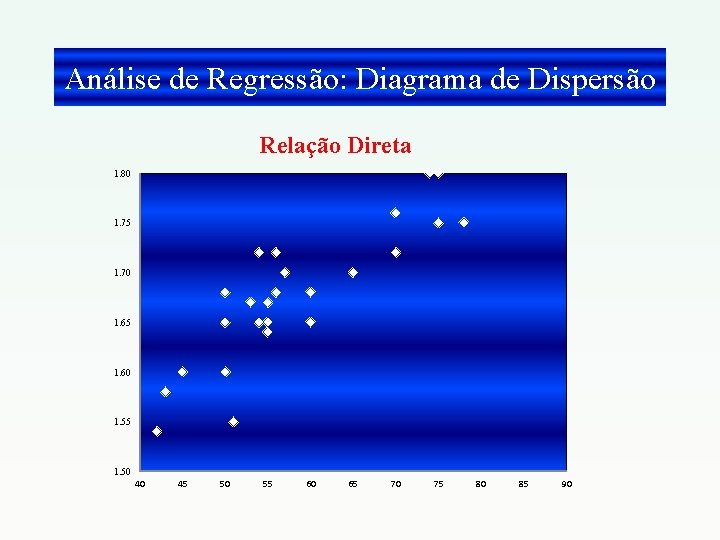
§ É uma “nuvem” de pontos plotados num gráfico cartesiano. § Os pontos são definidos pelos valores da variável X e da variável Y. § Numa pesquisa toda vez que os valores de X e Y forem apurados um par de informação referente a cada ponto é gerado. § Os valores das variáveis x e y serão as coordenadas de Variável Y Análise de Regressão: Diagrama de Dispersão Variável X

Análise de Regressão: Diagrama de Dispersão Relação Direta 1. 80 1. 75 1. 70 1. 65 1. 60 1. 55 1. 50 40 45 50 55 60 65 70 75 80 85 90

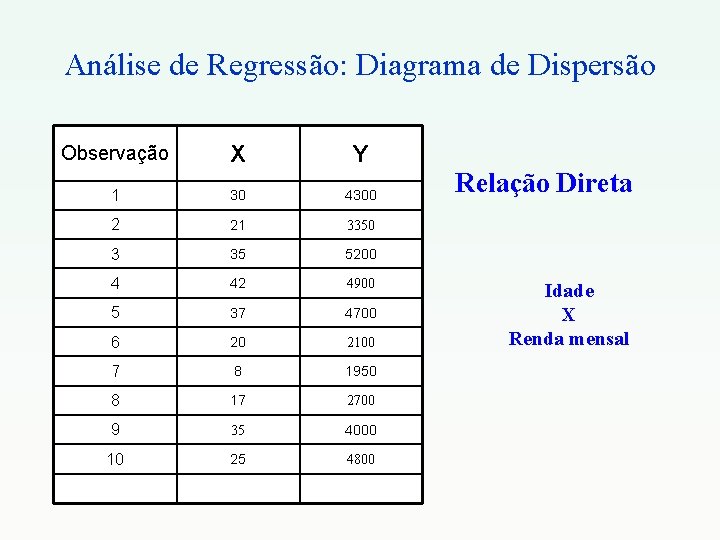
Análise de Regressão: Diagrama de Dispersão Observação X Y 1 30 4300 2 21 3350 3 35 5200 4 42 4900 5 37 4700 6 20 2100 7 8 1950 8 17 2700 9 35 4000 10 25 4800 Relação Direta Idade X Renda mensal

Análise de Regressão: Diagrama de Dispersão Relação Direta Idade x Renda

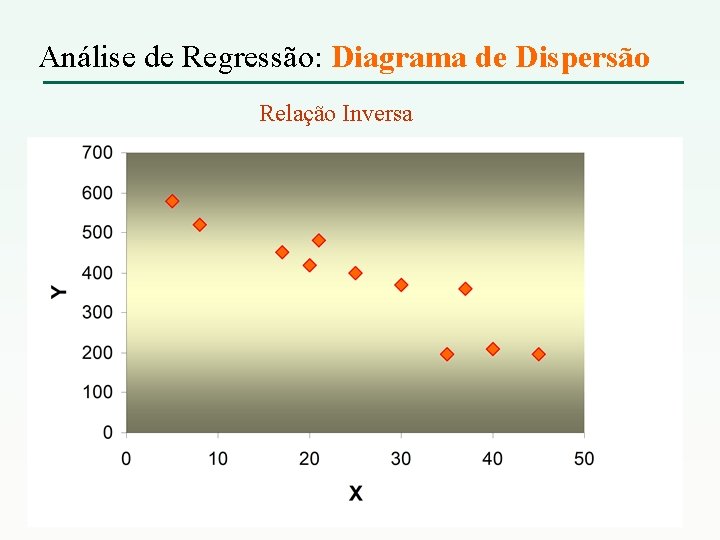
Análise de Regressão: Diagrama de Dispersão Relação Inversa

Análise de Regressão: Diagrama de Dispersão x y 30 21 35 370 480 195 45 195 20 8 17 40 25 5 3 420 520 450 210 400 580 640 Relação Inversa Distancia em relação do centro da cidade X Renda familiar

Análise de Regressão: Diagrama de Dispersão

Análise de Regressão: Diagrama de Dispersão Sem relação

Modelo Linear Simples

Análise de Regressão: Modelo Linear • A Análise de Regressão é o processo matemático para calcular os parâmetros “a” e “b” de uma função f (X). Y = a + b X • Estes parâmetros determinam as características da função que relaciona ‘Y’ com ‘X’. • No caso do modelo linear esta função é representada por uma reta chamada de reta de regressão.

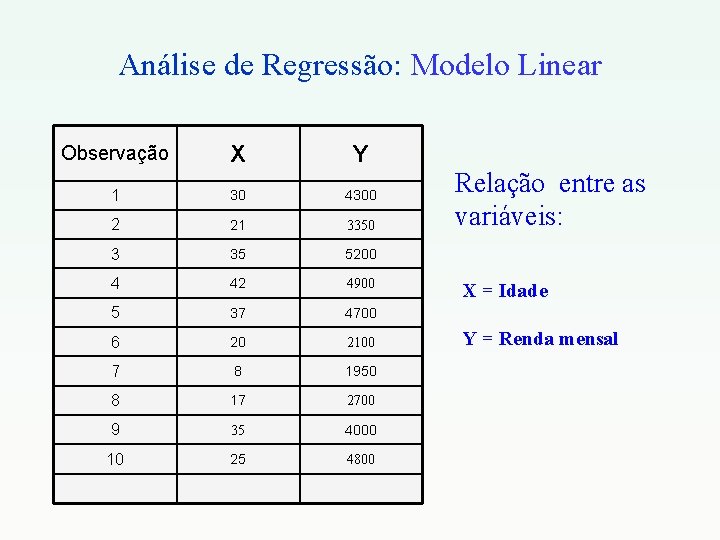
Análise de Regressão: Modelo Linear Observação X Y 1 30 4300 2 21 3350 3 35 5200 4 42 4900 5 37 4700 6 20 2100 7 8 1950 8 17 2700 9 35 4000 10 25 4800 Relação entre as variáveis: X = Idade Y = Renda mensal

Análise de Regressão: Modelo Linear

Análise de Regressão: Modelo Linear • A reta de regressão explica teoricamente ou modela a relação entre X e Y. • Isto significa que o valor de Y observado nem sempre é igual ao valor de Y’ estimado (ou previsto) pela reta de regressão.

Análise de Regressão: Modelo Linear Erro ou Desvio • Haverá sempre alguma diferença entre o valor observado Y e o valor estimado Y’. Essa diferença em estatística é chamada de erro ou desvio: e = Y – Y’ • O erro indica que: § que as variações de Y não são perfeitamente explicadas pelas variações de X ou; § que existem outras variáveis das quais Y depende ou; § que os valores de X e Y são obtidos de uma amostra particular que não é representativa da realidade.

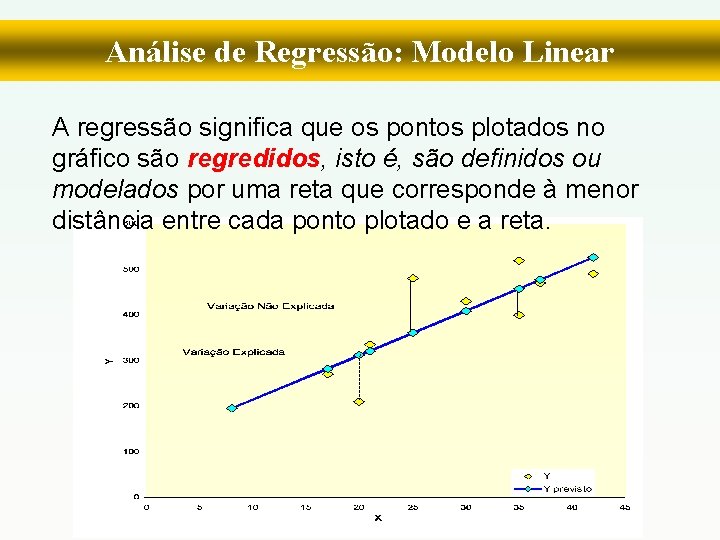
Análise de Regressão: Modelo Linear • A regressão significa que os pontos plotados no gráfico são regredidos, isto é, são definidos ou modelados por uma reta que corresponde à menor distância entre cada ponto plotado e a reta. § Y = α + β X equação da reta a partir dos dados coletados § Y’ = a + b X’ equação da reta a partir das estimativas

Análise de Regressão: Modelo Linear A regressão significa que os pontos plotados no gráfico são regredidos, isto é, são definidos ou modelados por uma reta que corresponde à menor distância entre cada ponto plotado e a reta.

Análise de Regressão: Modelo Linear ! ! ! ! O objetivo da regressão ! ! ! ! § Reduzir a diferença entre Y (plotado) e Y’(estimado) ou; § Tornar mínimo os somatórios desvios entre Y e Y’. (Y – Y’) = (y 1 -y’ 1)+(y 2 -y’ 2)+. . +(yn - y’n) = mínimo

Análise de Regressão: Modelo Linear

Análise de Regressão: Modelo Linear Método dos Mínimos Quadrados • É o método matemático para calcular os parâmetros a e b da reta regressão. • O método dos mínimos quadrados define uma reta que minimiza a soma das distâncias ao quadrado entre os pontos plotados (X, Y) e a reta (X’, Y’). • A reta que minimiza as distâncias ou as diferenças (ou o erro) entre Y e Y’ é chamada de curva de regressão • Equações Normais: § Σ XY = a Σ X + b Σ X 2 § Σ Y = Na + b Σ X

Análise de Regressão: Modelo Linear

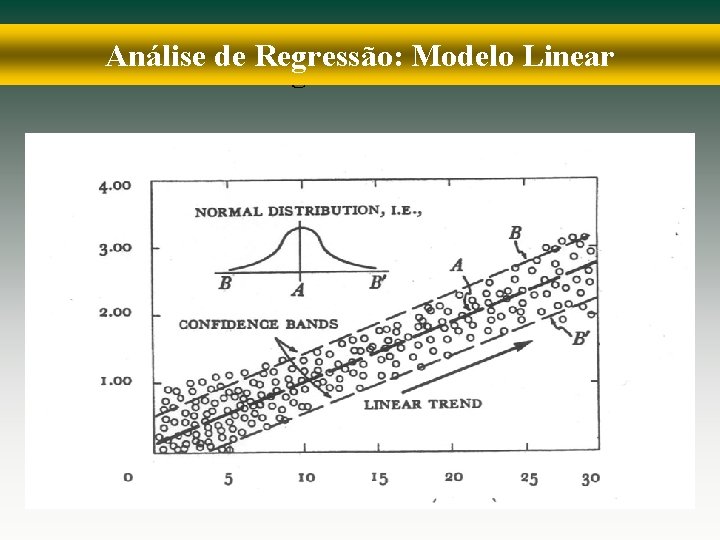
Análise de Regressão: Modelo Linear UTILIDADE DA RETA DE REGRESSÃO § A reta de regressão é apenas uma aproximação da realidade. § É um modo útil para indicar a tendência dos dados. Mas até que ponto a reta de regressão é uma aproximação confiável para avaliar a tendência da realidade? §Duas medidas são usadas para indicar o quanto confiável, útil ou aproximada da realidade é a reta: Erro padrão da estimativa Coeficiente de determinação

Análise de Regressão: Modelo Linear Erro Padrão da Estimativa - Se • Mede o desvio entre os valores reais de Y e os valores estimados Y’. • Ele informa a extensão do erro entre os valores de Y’ obtidos das estimativas e os valores de Y fornecidos pela amostra. • Se é medido na unidade de Y. O que se busca é obter o menor valor possível de Se. • Pode-se interpretar o Se como um desvio padrão dos resíduos.

Análise de Regressão: Modelo Linear Y’ Y’ Y Y Y’ Y’ Y’

Análise de Regressão: Modelo Linear Erro Padrão da Estimativa Se • Assumindo que estes resíduos são "normalmente distribuídos", pode-se dizer então que: 68% 95% dos pontos (plotados) encontram-se dentro do intervalo de 1 desvio padrão entorno da média: -1 ≤ Se ≥ +1 dos pontos encontram-se dentro do intervalo de 2 desvios padrão ao redor da média: -2 ≤ Se ≥ +2 • Fórmula • Se 2 Σ (Y – Y’)2 = Se = N – 2 Σ (Y – Y’)2 N – 2

Análise de Regressão: Modelo Linear Coeficiente de Determinação • Observe que os pontos (xi, yi) estão distribuídos acima e abaixo da reta de regressão. • Para cada ponto (Y) coletado no levantamento de campo : –

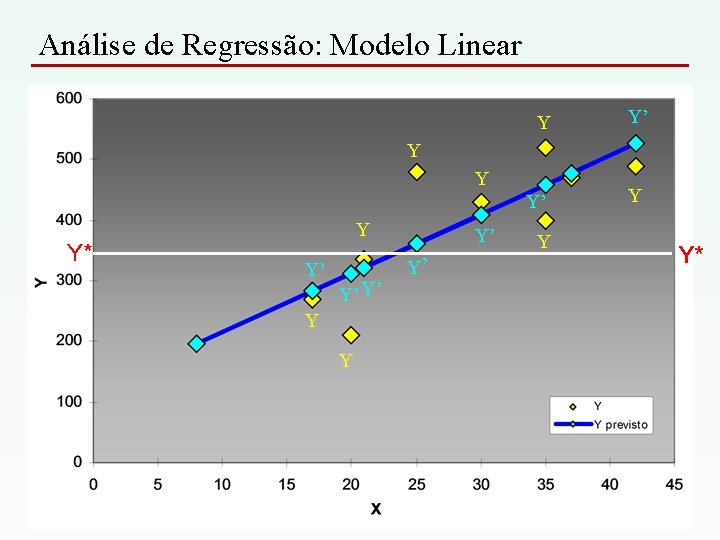
Análise de Regressão: Modelo Linear Y Y’ Y* Y Y’ Y’ Y’ Y Y Y*

Análise de Regressão: Modelo Linear • A diferença entre o valor de Y* é a variação total. Y - Y* • A diferença entre o valor de Y’ é chamada de variação Não explicada. Y – Y’ • A diferença entre o valor de Y* e o valor de Y’ é o chamada de variação explicada Y’ – Y*

Análise de Regressão: Modelo Linear • A soma dos desvios ao quadrado entre todos os pontos e a média de Y é chamada de Variação Total Σ (Y – Y*)2 • A soma dos desvios ao quadrado entre os valores de Y’ é chamada de Variação Não Explicada Σ ( Y – Y’)2 • A soma dos desvios ao quadrado entre os valores de Y* e os valores de Y’ é chamada de Variação Explicada

Análise de Regressão: Modelo Linear Coeficiente de Determinação Σ (Y – Y*)2 Variação Total Σ (Y – Y’)2 Σ (Y’ – Y*)2 Variação Não Explicada Variação Total = Variação não Explicada + Variação Explicada Σ (Y – Y*)2 = Σ (Y – Y’)2 + Σ (Y’ – Y*)2

Análise de Regressão: Modelo Linear Coeficiente de Determinação r 2 = Σ (Y’ – Y*)2 _________ Σ (Y – Y*)2 Variação Explicada Variação Total • O coeficiente de determinação deve ser interpretado como: Ø a proporção entre a variação total da variável dependente Y e a variação de Y que é explicada pela da variável independente X. Ø O porcentual de variação da variável Y que é explicado pela variável X.

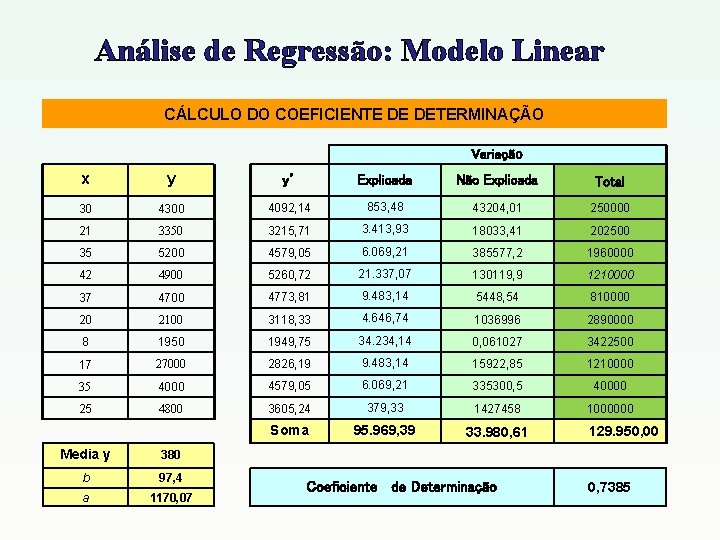
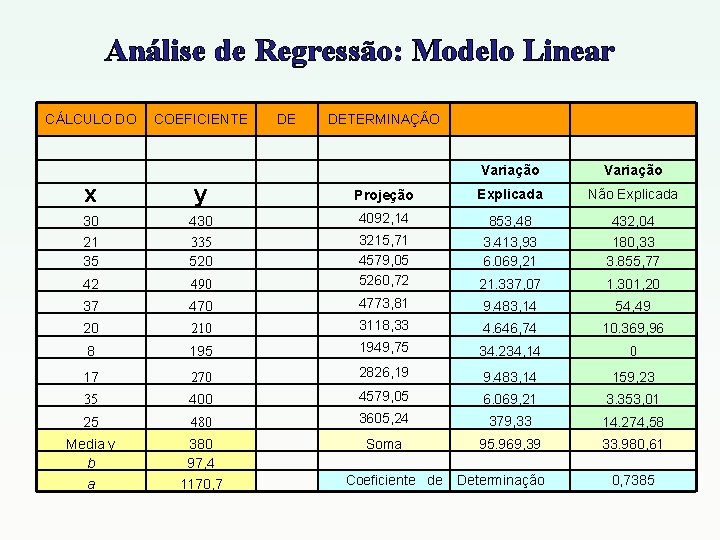
Análise de Regressão: Modelo Linear CÁLCULO DO COEFICIENTE DE DETERMINAÇÃO Variação x y y’ Explicada Não Explicada Total 30 4300 4092, 14 853, 48 43204, 01 250000 21 3350 3215, 71 3. 413, 93 18033, 41 202500 35 5200 4579, 05 6. 069, 21 385577, 2 1960000 42 4900 5260, 72 21. 337, 07 130119, 9 1210000 37 4700 4773, 81 9. 483, 14 5448, 54 810000 20 2100 3118, 33 4. 646, 74 1036996 2890000 8 1950 1949, 75 34. 234, 14 0, 061027 3422500 17 27000 2826, 19 9. 483, 14 15922, 85 1210000 35 4000 4579, 05 6. 069, 21 335300, 5 40000 25 4800 3605, 24 379, 33 1427458 1000000 Soma 95. 969, 39 33. 980, 61 Media y 380 b 97, 4 a 1170, 07 Coeficiente de Determinação 129. 950, 00 0, 7385

Análise de Regressão: Modelo Linear CÁLCULO DO COEFICIENTE DE DETERMINAÇÃO Variação x y Projeção Explicada Não Explicada 30 4092, 14 853, 48 432, 04 21 35 335 520 3. 413, 93 6. 069, 21 180, 33 3. 855, 77 42 490 3215, 71 4579, 05 5260, 72 21. 337, 07 1. 301, 20 37 470 4773, 81 9. 483, 14 54, 49 20 210 3118, 33 4. 646, 74 10. 369, 96 8 195 1949, 75 34. 234, 14 0 17 270 2826, 19 9. 483, 14 159, 23 35 400 4579, 05 6. 069, 21 3. 353, 01 25 480 3605, 24 379, 33 14. 274, 58 Media y b 380 97, 4 Soma 95. 969, 39 33. 980, 61 a 1170, 7 Coeficiente de Determinação 0, 7385

Análise de Regressão: Modelo Linear Coeficiente de Correlação Simples “ r ” • O coeficiente de correlação é igual a raiz quadrada do coeficiente de determinação. • No exemplo anterior: Podemos obter o coeficiente de correlação a partir do coeficiente de determinação. : § r 2 = 0, 738 coeficiente de determinação § r = 0, 85 coeficiente de correlação. • O coeficiente de determinação é sempre positivo. • O coeficiente de correlação assume valores negativos e positivos.

Análise de Regressão: Modelo Linear Coeficiente de Correlação Simples • Valores de r igual ou próximos de 1 ou – 1 indicam que existe uma forte correlação entre as variáveis: Ø Valores próximos de +1 relação : direta Alta correlação entre Ø Valores próximos de -1 Ø Valores próximos de 0 (zero) as variáveis relação: inversa não há relação entre as variáveis. -1≤ r ≤ +1 o O coeficiente de determinação indica o grau de ajuste (fit) da reta de regressão. o O coeficiente de correlação é uma medida que indica a força da relação entre as variáveis

Análise de Regressão: Modelo Linear Resumindo • Os valores de r estão limitados entre -1 ≤ r ≤ +1 • O coeficiente de correlação tem um valor único para a população ou amostra. • Coeficiente de correlação padroniza dentro dos horizontes acima as variações da covariância

Análise de Regressão: Modelo Linear • Por isso o coeficiente de correlação pode ser expresso: r. X, Y = Cov (X, Y) σX σY • σX – • σY – • Cov (X, Y) – desvio padrão da variável X desvio padrão da variável Y Covariância de X e Y

Análise de Regressão: Modelo Linear Análise dos coeficientes • Em razão da variação amostral, o modelo de regressão calculado é apenas um dos possíveis modelos extraídos da população. • Supondo que o modelo baseado na população seja: Y = α +β X • e o modelo obtido da amostra seja: Y’ = a +b X + e • Onde e é o erro entre as observações e as estimativas da equação • Temos que os valores dos coeficientes a e b da equação de regressão obtidos de uma amostragem aleatória não são iguais aos valores α e β da população.

Análise de Regressão: Modelo Linear • Erro Padrão do Coeficiente ‘b’ (Sb) § O erro padrão de b indica o quanto o coeficiente b da equação de regressão se distancia do coeficiente β da população. S 2 e § Fórmula Sb = √ S 2 b = = Se (n-1) x Var (x) √ (n-1) x Var (x) Pela fórmula conclui-se que o erro padrão do coeficiente b: • é diretamente proporcional ao erro padrão da estimativa Se, e; • e inversamente proporcional ao valor do desvio padrão de x e o tamanho da amostra menos 1.

Análise de Regressão: Modelo Linear • Erro Padrão do Coeficiente ‘a’ (Sa) § O erro padrão do coeficiente a indica o quanto o coeficiente a da equação de regressão se distancia (ou desvia) do coeficiente α da população. 1 X 2 § Fórmula Sa = Se + √ n (n-1) x S 2 x Pela fórmula conclui-se que o erro padrão do coeficiente a: • é também diretamente proporcional ao erro padrão da estimativa Se, e; • reduz seu valor com o valor do desvio padrão de x e o tamanho da amostra menos 1.

Modelo Linear Complexo

Análise de Regressão: Modelo Multivariado • Modelo Linear Complexo § Quando há relação linear com mais de uma variável independente: Y = a + b 1 X 1 + b 2 X 2 +. . . + bk Xk § Quando existirem 2 variáveis independentes os pontos serão plotados em gráfico tridimensional, isto é, um gráfico com três eixos (y, x 1 e x 2). § Nestes casos os pontos não serão regredidos para uma linha reta, mas para um plano. § Quando mais de 2 variáveis independentes são usadas na equação os pontos são regredidos para o que é chamado de Hiperplano. § As hipóteses do modelo linear continuam válidas no modelo do plano: intervalos de confiança, distribuição normal do erro e correlação.

Análise de Regressão: Modelo Multivariado

Análise de Regressão: Modelo Multivariado • Ajuste do Plano: Método dos Mínimos Quadrados • O ajuste do plano (plane best fit), é também calculado pelo método dos mínimos quadrados (neste caso as equações normais são escritas na forma de matriz). • Minimizar Σ (Yi -Y’)2 = d 2 • Minimizar Σ [Yi – a - b 1 (X 1 – X 1*) – b 2 (X 2 – X 2*) ] 2 d 11 d 12 b 1 = g 1 d 21 d 22 b 2 g 2 • Equações Normais • Σ Yi = a n + b 1 ΣX 1 i + b 2 ΣX 2 i • Σ Yi X 1 i = a Σ X 1 i + b 1 Σ( X 1 i )2 + b 2 Σ ( X 1 i X 2 i ) • Σ Yi X 2 i = a Σ X 2 i + b 1 Σ (X 1 i X 2 i ) + b 2 Σ ( X 2 i )2

Análise de Regressão: Modelo Multivariado Erro Padrão da Estimativa para modelos multivariados O cálculo do desvio padrão das diferenças entre o Yi (levantado) e o Y’ (estimado) é igual ao do modelo linear simples: 1 S 2 eec = Ʃ (yi – a – b 1 x 1 – b 2 x 2) n-k-1 k – no. de variáveis N-k-1 – graus de liberdade

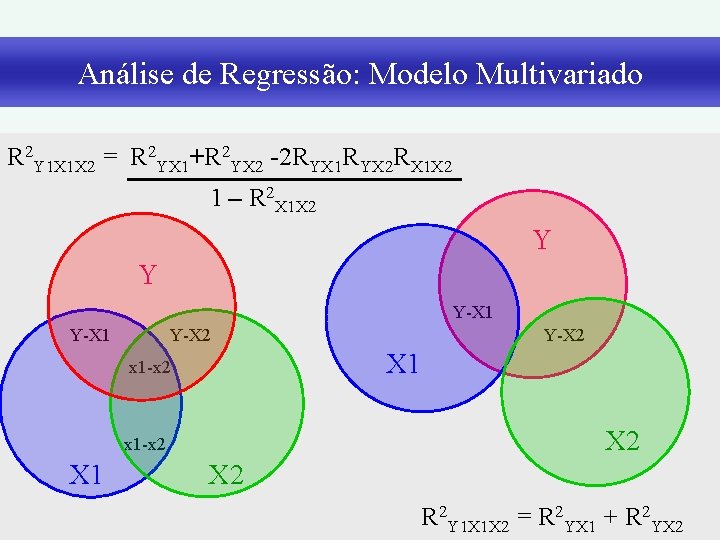
Análise de Regressão: Modelo Multivariado • Coeficiente de Correlação Complexo “ R” § Semelhante ao coeficiente de correlação simples (regressão linear). § Neste caso deve-se cuidar para evitar intercorrelação ou multicolinearidade entre as variáveis independentes. § Nos modelos lineares complexos a correlação entre duas variáveis independentes (r) não deve ser maior ou mesmo próxima da correlação complexa (R), entre y e as duas x independentes. R 2 YX 1 + R 2 YX 2 – 2 RYX 1 RYX 2 RX 1 X 2 R 2 YX 1 X 2 = -------------------1 – R 2 X 1 X 2

Análise de Regressão: Modelo Multivariado • Coeficiente de Correlação Complexo “ R” b 1 Σ Yi ( X 1 i – X 1 * + b 2 RYX 1 X 2 = Σ Yi ( X 2 i – X 2* +. . . + bn Σ Yi ( Xn i – Xn* Σ (Yi – Y*)2 RYX 1 X 2 = R 2 YX 1 + R 2 YX 2 – 2 RYX 1 RYX 2 RX 1 X 2 ----------------------1 – R 2 X 1 X 2

Análise de Regressão: Modelo Multivariado • Coeficientes de Correlação Parciais RYX 1 = Σ (Y’ – Y*)2 -1/2 Coeficiente de Correlação Parcial YX 1 Σ (Y – Y*)2 RYX 2 = Σ (Y’ – Y*)2 -1/2 Coeficiente de Correlação Parcial YX 2 Σ (Y – Y*)2 • RX 1 X 2 = Σ (Y’ – Y*)2 -1/2 Σ (Y – Y*)2 Coeficiente de Correlação Parcial X 1 X 2

Análise de Regressão: Modelo Multivariado R 2 Y 1 X 1 X 2 = R 2 YX 1+R 2 YX 2 -2 RYX 1 RYX 2 RX 1 X 2 1 – R 2 X 1 X 2 Y Y-X 1 Y-X 2 x 1 -x 2 X 1 x 1 -x 2 X 2 X 1 X 2 R 2 Y 1 X 1 X 2 = R 2 YX 1 + R 2 YX 2

Análise de Regressão: Modelo Multivariado • Regressão por Etapas (stepwise regression) § É o processo de inclusão/exclusão de variáveis independentes em função da contribuição das mesmas para a explicação das variações de Y (isto é, para o incremento de R). § A variável independente x com a maior correlação parcial em relação a variável dependente y deve ser mantida. § O pesquisador deve avaliar até que ponto ele deve adicionar mais variáveis independentes ao modelo: este ponto é atingido quando a adição de uma variável pouco contribui para incrementar R.
 Desordem e regresso bandeira
Desordem e regresso bandeira Anlise swot
Anlise swot Lienzo rima
Lienzo rima Grado superlativo
Grado superlativo Tipo y subtipo
Tipo y subtipo Tipos de narrador
Tipos de narrador Relación paradigmática
Relación paradigmática Que es un narrador objetivo
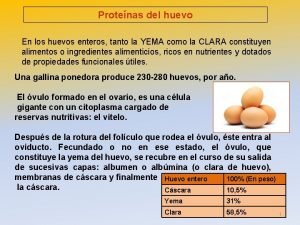
Que es un narrador objetivo Los huevos son proteinas
Los huevos son proteinas Conjunto planetario
Conjunto planetario Herencia intermedia
Herencia intermedia El objetivo de un texto expositivo
El objetivo de un texto expositivo Algoritmos que es
Algoritmos que es Fractura tipo chance
Fractura tipo chance Ejemplos de conclusiones de trabajos
Ejemplos de conclusiones de trabajos H-o-h tipo de enlace
H-o-h tipo de enlace Que es gametogenia
Que es gametogenia Intentalo completa las preguntas con que o cual
Intentalo completa las preguntas con que o cual Tipos de ambiente en la narración
Tipos de ambiente en la narración Las falacias no formales
Las falacias no formales Tipo di radice
Tipo di radice Tipos de neuronas
Tipos de neuronas Gneas
Gneas Floculador tipo alabama
Floculador tipo alabama Un hombre rico que tipo de texto es
Un hombre rico que tipo de texto es Respuestas
Respuestas Error tipo alfa y beta
Error tipo alfa y beta Tipos de arcos arquitetura
Tipos de arcos arquitetura Que historias narraban los juglares
Que historias narraban los juglares El hospital como empresa de servicio
El hospital como empresa de servicio Caratterizzazione dei personaggi
Caratterizzazione dei personaggi Transtorno bipolar tipo 2
Transtorno bipolar tipo 2 Australóide
Australóide Falconer incision
Falconer incision Alteração
Alteração Cultura tipo club
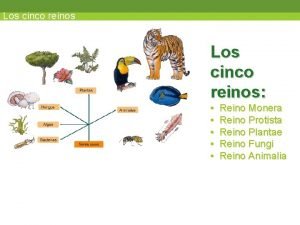
Cultura tipo club Los cinco reinos protista
Los cinco reinos protista Tipos abstratos de dados
Tipos abstratos de dados Importancia de las relaciones humanas
Importancia de las relaciones humanas Tipo de texto cientifico
Tipo de texto cientifico Magma
Magma Tenedores en ingles
Tenedores en ingles Oligodendrocitos
Oligodendrocitos Tipos de diagrama matricial
Tipos de diagrama matricial Que son textos sociales
Que son textos sociales Caule aquatico
Caule aquatico Dsav classificação de rastelli
Dsav classificação de rastelli Cooperative tipo a e b
Cooperative tipo a e b Planos de rastros tipo tif
Planos de rastros tipo tif Reaccion de sustitucion simple
Reaccion de sustitucion simple Tipo penal
Tipo penal Funcion de membrana plasmatica
Funcion de membrana plasmatica Sutura sarnoff
Sutura sarnoff Tipo de grafo
Tipo de grafo Estructura interna de un anuncio publicitario
Estructura interna de un anuncio publicitario