Agenda Lecture Content Recurrence Relations Solving Recurrence Relations

Agenda • Lecture Content: § Recurrence Relations § Solving Recurrence Relations § Iteration § Linear homogenous recurrence relation of order k with constant coefficients • Exercise

Recurrence Relations

Recurrence Relations § Relates the n-th element of a sequence to its predecessors. Example: an = 9 * an-1 § Closely related to recursive algorithms. § Suited for analysis of algorithm

Recurrence Relations § Generate a sequence : 1. Start with 5 2. Given any term, add 3 to get the next term 5, 8, 11, 14, … § Sequence {an} = a 0, a 1, …, an-1, an 1. a 0= 5 initial condition 2. an = an-1 + 3 , n ≥ 1 recurrence relation

Recurrence Relations for the sequence {an} § is an equation that expresses an in terms of one or more of the previous terms of the sequence, namely, a 0, a 1, …, an-1 for all integers n with n ≥ n 0, where n 0 is a nonnegative integer. § A sequence {an} is called a solution of a recurrence relation if its terms an satisfy the recurrence relation.

Motivation One of the main reason for using recurrence relation is that sometimes it is easier to determine the n-th term of a sequence in terms of its predecessors than it is to find an explicit formula for the n-th term in terms of n.

Example § Let {an} be a sequence that satisfies the recurrence relation an = an-1 – an-2 for n = 2, 3, 4, … and suppose that a 0 = 3 and a 1 = 5. What are a 2 and a 3? § a 2 = a 1 – a 0 = 5 – 3 = 2 § a 3 = a 2 – a 1 = 2 – 5 = -3 § Also a 4, a 5, …

Exercises § Find the first six terms of the sequence defined by the following recurrence relations: an = an-1 + an-3 a 0 = 1, a 1 = 2, a 2 = 0 an = n. an-1 + (an-2)2 a 0 = -1, a 1 = 0

Example § Find the recurrence relation of: - {an} = (0, 1, 2, 3, …) - {an} = (5, 10, 15, 20, …) § Find the first three terms of the sequence defined by the following recurrence relations: - an = 3 * an-1 – an-2 a 0 = 3 and a 1 = 5 - an = an-1 – an-2 + an-3 a 0 = 3, a 1 = 5 and a 2 = 5

Modelling with Recurrence Relations (1) § The number of bacteria in a colony doubles every hour. If a colony begins with five bacteria, how many will be present in n hours? - a 0 = 5 - a 1 = 10 - a 2 = 20 - … § The number of bacteria at the end of n hours: an = 2 * an-1

Modelling with Recurrence Relations (2) § Suppose that a person deposits $ 10, 000 in a saving account at a bank yielding 11% per year with interest compounded annually. How much will be in the account after 30 years? • • • Pn : the amount in the account after n years Pn = Pn-1 + 0. 11 Pn-1 = 1. 11 Pn-1 P 0 = 10, 000 P 1 = 1. 11 P 0 P 2 = 1. 11 P 1 = 1. 11 * 1. 11 P 0 = (1. 11)2 P 0 Pn = (1. 11)n P 0 Deriving explicit formula from the recurrence relation and its initial condition (Section 7. 2)

Converting to a Recursive Algorithm § § A recursive function is a function that invokes itself. A recursive algorithm is an algorithm that contains a recursive function Input: n, the number of years Output: the amount of money at the end of n years 1. 2. 3. 4. 5. compound_interest (n){ if (n == 0) return 10, 000 return 1. 11 * compound_interest (n-1) }

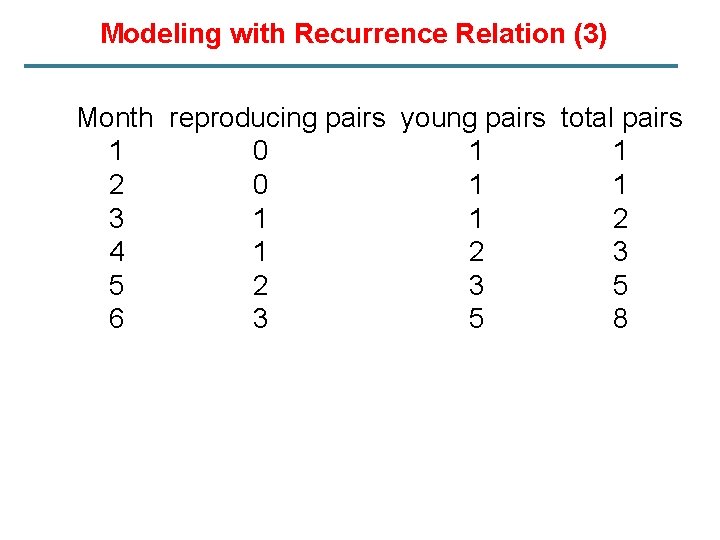
Modeling with Recurrence Relation (3) § A young pair of rabbits is placed on an island. A pair of rabbit does not breed until they are 2 months old. After they are 2 months old, each pair of rabbits produces another pair each month. Find a recurrence relation for the number of pairs of rabbit on the island after n months, assuming that no rabbits ever die. § fn : the number of pairs of rabbits after n months

Modeling with Recurrence Relation (3) Month reproducing pairs young pairs total pairs 1 0 1 1 2 0 1 1 3 1 1 2 4 1 2 3 5 6 3 5 8

Modeling with Recurrence Relation (3) § fn : the number of pairs of rabbits after n months § f 1 = 1 § f 2 = 1 § f 3 = 2 § fn = the number on the island for the previous month + the number of newborn pairs § fn = fn-1 + fn-2 Fibonacci Numbers

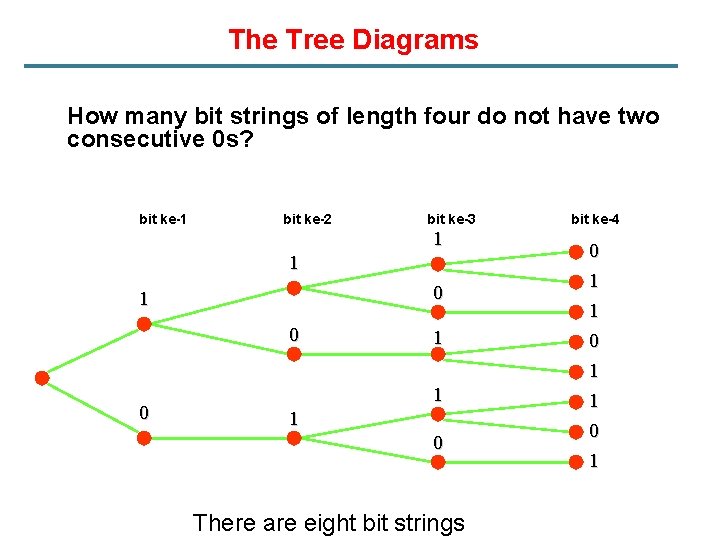
Modelling with Recurrence Relation (4) § Find a recurrence relation and give initial conditions for the number of bit strings of length n that do not have two consecutives 0 s. § an : the number of bit strings of length n that do not have two consecutive 0 s.

The Tree Diagrams How many bit strings of length four do not have two consecutive 0 s? bit ke-1 bit ke-2 bit ke-3 1 1 0 0 1 1 1 0 There are eight bit strings bit ke-4 0 1 1 0 1

Modelling with Recurrence Relation (4) an = an-1 + an-2 for n ≥ 3 § § a 1 = 2 0, 1 a 2 = 3 (01, 10, 11) a 3 = 5 (011, 010, 101, 110, 111) a 4 = 8

Solving Recurrence Relations

Solving Recurrence Relations - Given recurrence relations with sequence: a 0 , a 1 , … - Find an explicit formula for the general term: an - Two methods: - Iteration - Recurrence relations with constant coefficients

Iteration Steps: - Use the recurrence relation to write the n-th term an in terms of certain of its predecessors an-1 , …, a 0 - Use the recurrence relation to replace each of an-1 , … by certain of their predecessors. - Continue until an explicit formula is obtained.

Iteration: Example 1 an = an-1 + 3 a 0= 5 n≥ 1 Solution: - an-1 = an-2 + 3 - an = an-1 + 3 = (an-2 + 3) + 3 = an-2 + 2. 3 = (an-3 + 3) +2. 3 = an-3 + 3. 3 = an-k + k. 3 …k=n = a 0 + n. 3 =5+n. 3

Iteration: Example 2(1) § The number of bacteria in a colony doubles every hour. If a colony begins with five bacteria, how many will be present in n hours? § a 0 = 5 § a 1 = 10 § a 2 = 20 § … § The number of bacteria at the end of n hours: an = 2 * an-1

Iteration: Example 2(2) an = 2 * an-1 = 2 * (2 * an-2 ) = 2 * 2 ( an-2 ) = 2 * (2 * an-3 ) = 23 ( an-3 ) … = 2 n * a 0 = 2 n * 5

Iteration: Example 3 § The deer population is 1000 at time n = 0 § The increase from time n-1 to time n is 10 percent. § Find the recurrence relation, initial condition and solve the recurrence relation at time n § § § a 0 = 1000 an = 1. 1 * an-1 an = 1. 1 * (1. 1 * an-2) = 1. 12 * an-2 an = 1. 1 n * a 0 an = 1. 1 n * 1000

Recurrence Relations with Constant Coefficients

Definition § A linear homogeneous recurrence relation of order k with constant coefficients is a recurrence relation of the form: an = c 1 an– 1+ c 2 an– 2+ … + ckan–k , ck ≠ 0 § Example: • Sn = 2 Sn– 1 • fn = fn– 1 + fn– 2

Not linear homogenous recurrence relations § Example: • an = 3 an– 1 an– 2 • an – an– 1 = 2 n • an = 3 nan– 1 Why?

Solving Recurrence Relations § Example: • Solve the linear homogeneous recurrence relations with constant coefficients an = 5 an– 1 – 6 an– 2 a 0 = 7, a 1= 16 § Solution: • Often in mathematics, when trying to solve a more difficult instance of some problem, we begin with an expression that solved a simpler version.

Solving Recurrence Relations § For the first-order recurrence relation, the solution was of the form Vn= tn ; thus for our first attempt at finding a solution of the secondorder recurrence relation, we will search for a solution of the form Vn= tn. § If Vn = tn is to solve the recurrence relation, we must have Vn= 5 Vn– 1– 6 Vn– 2 or tn = 5 tn– 1 – 6 tn– 2 or tn – 5 tn– 1+ 6 tn– 2 = 0. Dividing by tn– 2, we obtain the equivalent equation t 2 – 5 t 1 + 6 = 0. Solving this, we find the solutions t= 2, t= 3. Characteristic roots polynomial

Solving Recurrence Relations § We thus have two solutions, Sn = 2 n and Tn = 3 n. • We can verify that if S and T are solutions of the preceding recurrence relation, then b. S + d. T, where b and d are any numbers, is also a solution of that relation. In our case, if we define the sequence U by the equation Un = b. Sn+ d. Tn = b 2 n + d 3 n, § U is a solution of the given relation.

Solving Recurrence Relations § To satisfy the initial conditions, we must have: 7 = U 0 = b 20 + d 30= b + d, 16 = U 1= b 21+ d 31= 2 b + 3 d. Solving these equations for b and d, we obtain b = 5, d = 2. § Therefore, the sequence U defined by Un= 5∙ 2 n + 2∙ 3 n satisfies the recurrence relation and the initial conditions. § We conclude that an= Un= 5∙ 2 n+ 2∙ 3 n, for n = 0, 1, ….

Theorem § Let an = c 1 an– 1+ c 2 an– 2 be a second-order, linear homogeneous recurrence relation with constant coefficients. • If S and T are solutions of the recurrence relation, then U = b. S+ d. T is also a solution of the relation. • If r is a root of t 2–c 1 t–c 2= 0, then the sequence rn, n = 0, 1, …, is a solution of the recurrence relation. • If a is the sequence defined by the recurrence relation, a 0 = C 0, a 1= C 1, and r 1 and r 2 are roots of the preceding equation with r 1 ≠ r 2, then there exist constants b and d such that an= br 1 n + dr 2 n, n = 0, 1, ….

Example (1) § More Population Growth • Assume that the deer population of Rustic County is 200 at time n = 0 and 220 at time n = 1 and that the increase from time n– 1 to time n is twice the increase from time n– 2 to time n– 1. • Write a recurrence relation and an initial condition that define the deer population at time n and then solve the recurrence relation.

Example (1) § Solution: • Let dn denote the deer population at time n. d 0 = 200, d 1 = 220 dn – dn-1 = 2(dn-1 – dn-2) dn = 3 dn-1 – 2 dn-2 • Solving t 2 – 3 t + 2 = 0, we have roots 1 and 2. Then the sequence d is of the form dn = b∙ 1 n + c∙ 2 n = b + c 2 n. • To meet the initial conditions, we must have 200 = d 0= b + c, 220 = d 1= b + 2 c. Solving for b and c, we find b= 180, and c= 20. • Thus, dn is given by dn = 180 + 20∙ 2 n.

Example (2) § Find an explicit formula for the Fibonacci sequence: fn – fn– 1 – fn– 2= 0, n≥ 3 f 1 = 1, f 2 = 1 § Solution: • We begin by using the quadratic formula to solve t 2 –t – 1 = 0. The solutions are t = (1 ±√ 5)/2. Thus the solution is of the form fn= b((1+√ 5)/2)n + c((1–√ 5)/2)n. – To satisfy the initial conditions, we must have b((1+√ 5)/2) + c((1–√ 5)/2)= 1, b((1+√ 5)/2)2+ c((1–√ 5)/2)2= 1. Solving these equations for b and d, we obtain b = 1/√ 5, d = -1/√ 5. • • Therefore, fn= 1/√ 5∙((1+√ 5)/2)n – 1/√ 5((1–√ 5)/2)n.

Theorem § Let an = c 1 an– 1 + c 2 an– 2 be a second-order, linear homogeneous recurrence relation with constant coefficients. • Let a be the sequence satisfying the relation and a 0 = C 0, a 1= C 1. • If both roots of t 2 – c 1 t – c 2 = 0 are equal to r, then there exist constants b and d such that an = brn + dnrn, n = 0, 1, ….

Example § Solve the recurrence relation dn= 4(dn-1 – dn-2) subject to the initial conditions d 0= 1 = d 1. – According to theorem, Sn= rn is a solution, where r is a solution of t 2 – 4 t + 4 = 0. Thus we obtain the solution Sn = 2 n. – Since 2 is the only solution of the equation, Tn= n 2 n is also a solution of the recurrence relation. – Thus the general solution is of the form U = a. S+ b. T. – We must have U 0 = 1 = U 1. The last equations become a. S 0 + b. T 0= a+ 0 b= 1, a. S 1+ b. T 1= 2 a+ 2 b = 1. – Solving for a and b, we obtain a = 1, b = -1/2. – Therefore, the solution is dn= 2 n – 1/2 n 2 n = 2 n – n 2 n-1.

Note § For the general linear homogeneous recurrence relation of order k with constant coefficients c 1, c 2, …, ck, • if r is a root of tk – c 1 tk-1 – c 2 tk-2 – … – ck = 0 of multiplicity m, it can be shown that rn, nrn, … , nm-1 rn are solutions of the equation.