Unrolling Carry Recurrence CarryLookahead Equations 4 Bit CLA

Unrolling Carry Recurrence

Carry-Lookahead Equations

4 -Bit CLA

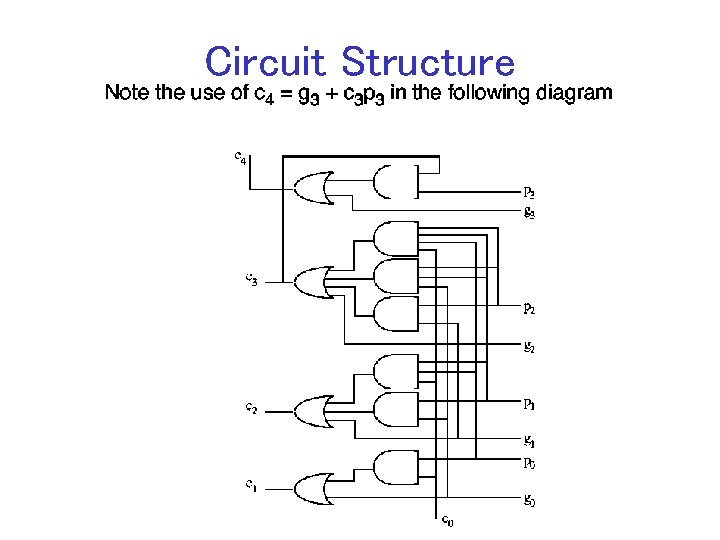
Circuit Structure

CLA Complexity

Managing CLA Complexity

Multilevel CLA Example

Radix-16 Addition • Two Binary Numbers Grouped into Hex Digits • Block Generate and Propagate Signals in Each radix-16 Digit • Replace c 4 Position of CLA Network with Block Signals g[i, i+3] and p[i, i+3] • Results in 4 -bit “Lookahead Carry Generator”

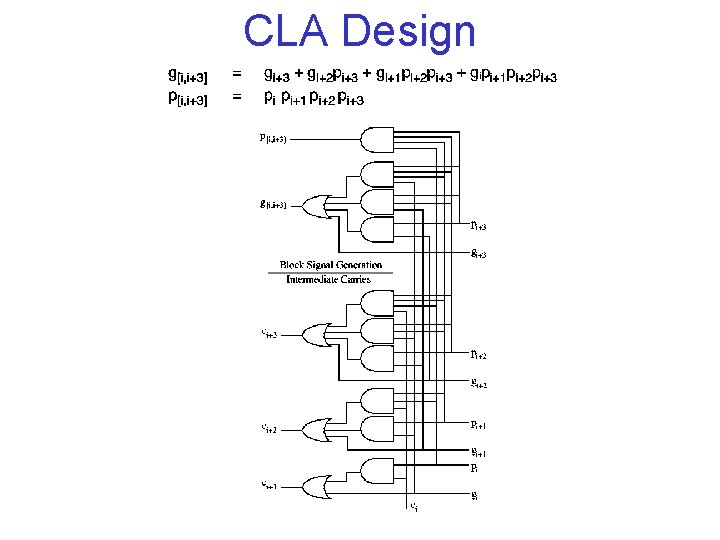
CLA Design

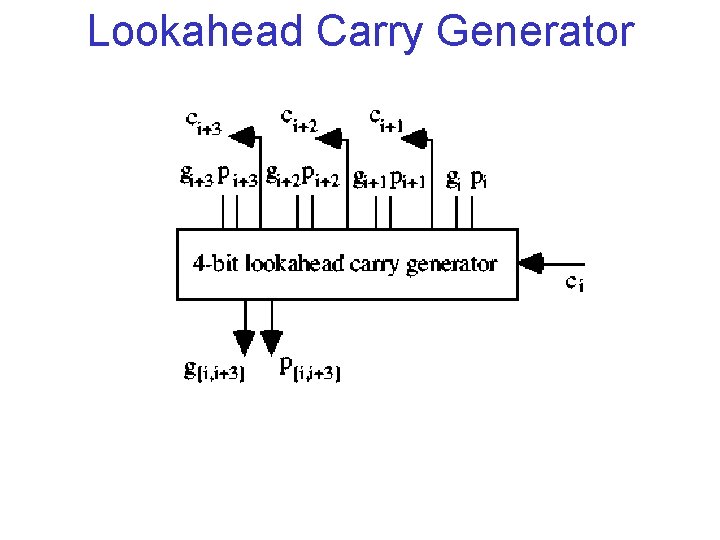
Lookahead Carry Generator

Block Generate and Propagate • Assume i 0 < i 1 < i 2 • Example: g[0, 3] is Generate Signal of Block for bits 0 -3 • Relationships Allow for Merging of Blocks • Can Allow Merged Block to Overlap

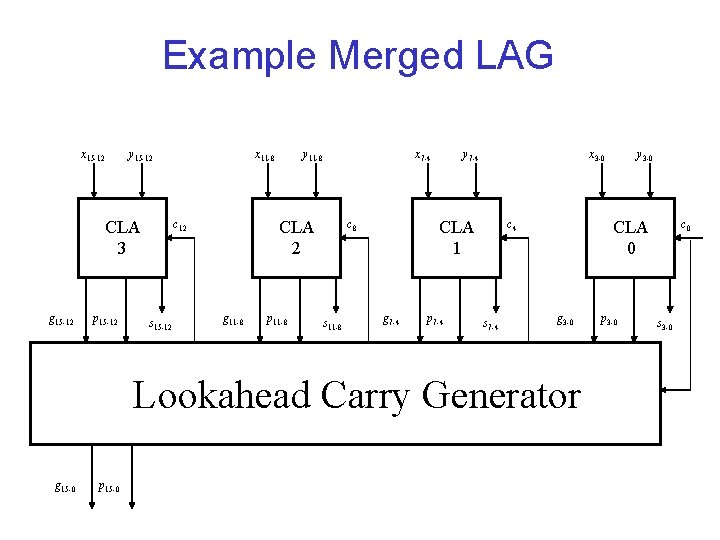
Example Merged LAG x 15 -12 y 15 -12 CLA 3 g 15 -12 p 15 -12 x 11 -8 x 7 -4 CLA 2 c 12 s 15 -12 y 11 -8 g 11 -8 p 11 -8 x 3 -0 CLA 1 c 8 s 11 -8 y 7 -4 g 7 -4 p 7 -4 CLA 0 c 4 s 7 -4 g 3 -0 Lookahead Carry Generator g 15 -0 p 15 -0 y 3 -0 p 3 -0 c 0 s 3 -0

CLA Latency

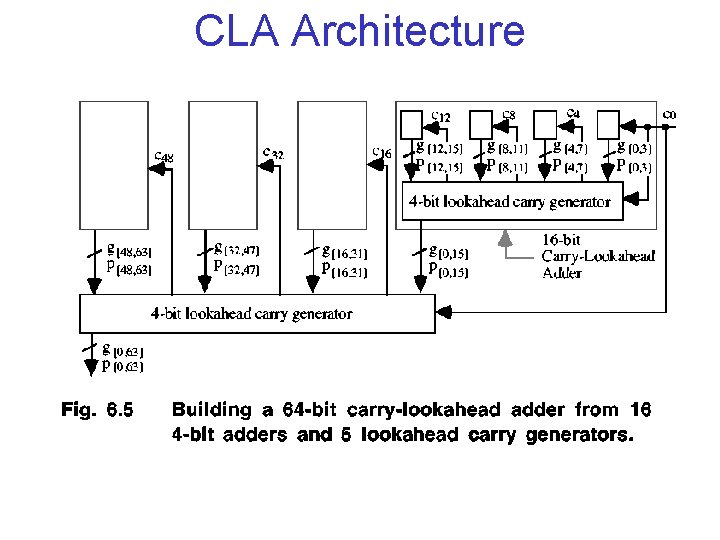
CLA Architecture

Overlapped LAGs • Overlap Blocks [i 1, j 1] and [i 0, j 0] • Relationships Become: • Useful for Building Trees of Different Shapes

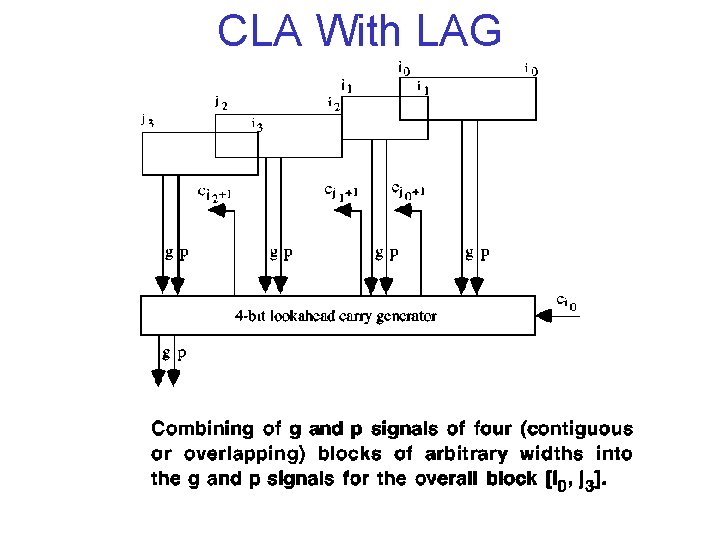
CLA With LAG

CLA Latency Example: 64 -bit CLA in 13 gate levels since 43 = 64 Generates final carry out for Fig. 6. 5

Ling Adders

Ling Adders – Wired OR

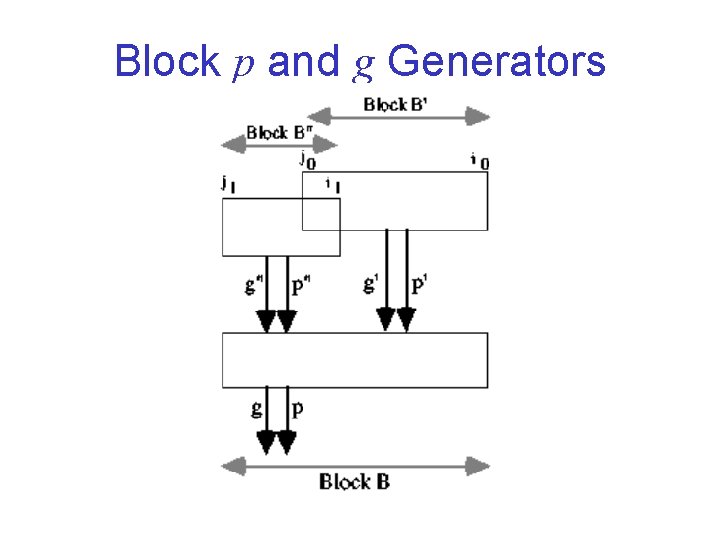
Block p and g Generators

Carry Determination as Prefix Computations • Two Contiguous (or Overlapping) Blocks (g , p ) and (g , p ) • Merged Block (g, p) g = g + g p p = p p • Large Group Generates Carry if: 1) left group generates carry 2) right group generates and left group propagates

Carry Operator, ¢ • Define Operator Over (g, p) Pairs (g, p) = (g , p ) ¢ (g , p ) g = g + g p p = p p • ¢ is Associative (g , p ) ¢ (g , p ) = [(g , p ) ¢ (g , p ) ] ¢ (g , p ) = (g , p ) ¢ [(g , p ) ¢ (g , p )]

Carry Operator, ¢ (cont) • ¢ is NOT Commutative (g , p ) ¢ (g , p )¢ (g , p ) • This is Easy to See Because: g = g + g p g + g p

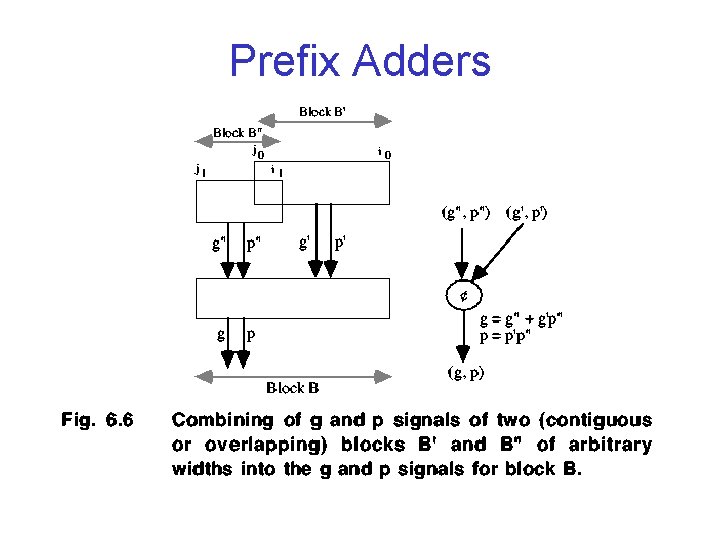
Prefix Adders

Carry Determination • Assume Adder with NO c. IN ci+1 = g[0, i] • Carry Enters i+1 Block iff Generated in Block [0, i] • Assume Adder with c. IN = 1 • Viewed as Generated Carry from Stage -1 p-1 = 0, g-1 = c. IN • Compute g[-1, i] For All i • Formulate Carry Determination as:

Prefix Computation

Prefix Sums Analogy • Designs for Prefix Sums Can be Converted to Carry Computation • Replace Adder with ¢ Operator • Addition IS Commutative, Order Doesn’t Matter • Can Group (g, p) In Anyway to Combine Into Block Signals (as long as order is preserved) • (g, p) Allow for Overlapping Groups, Prefix Sums Does Not (sum would contain some values added two or times)

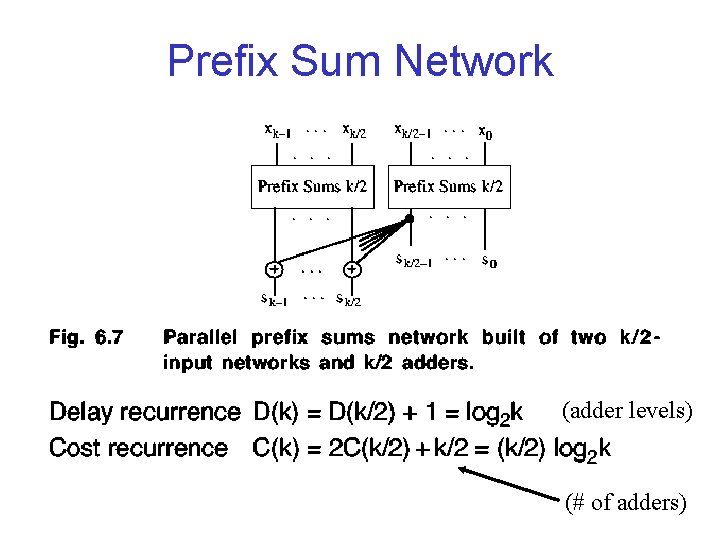
Prefix Sum Network (adder levels) (# of adders)

Another Way for Prefix Sums • Compute the Following First: x 0+x 1 x 2+x 3 x 4+x 5 . . . xk-2+xk-1 • Yields the Partial Sums, s 1, s 3, s 5, . . . , sk-1 • Next, Even Indexed Sums Computed As: s 2 j = s 2 j-1 + x 2 j

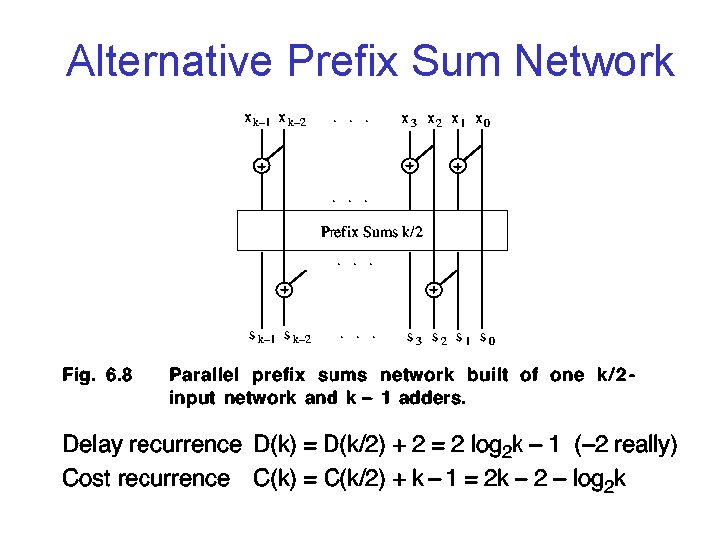
Alternative Prefix Sum Network

Comparison of Prefix Sum Networks • First Design Faster: lg 2(k) versus 2 lg 2(k)-2 (levels) • First Design has High Fan-out Requirements • First Design Requires More Cells (k/2)lg 2 k versus 2 k-2 -lg 2 k • Second Design is Brent-Kung Parallel Prefix Graph • First Design is Kogge-Stone Parallel Prefix Graph (fan-out can be avoided by distributing computations)

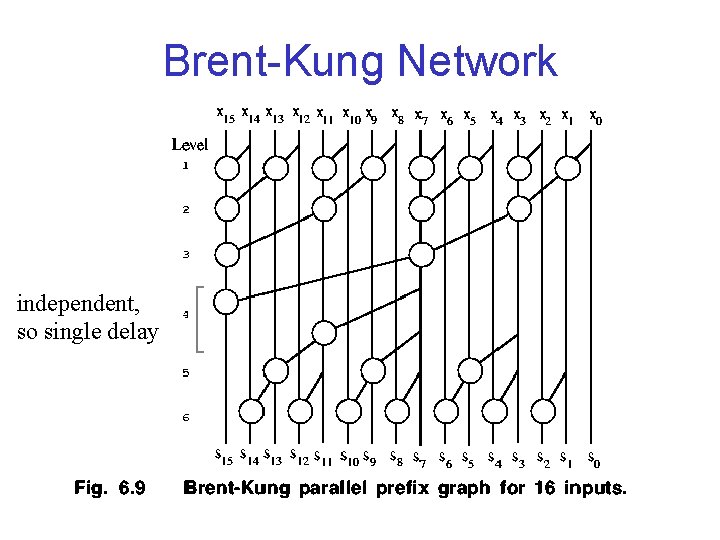
Brent-Kung Network independent, so single delay

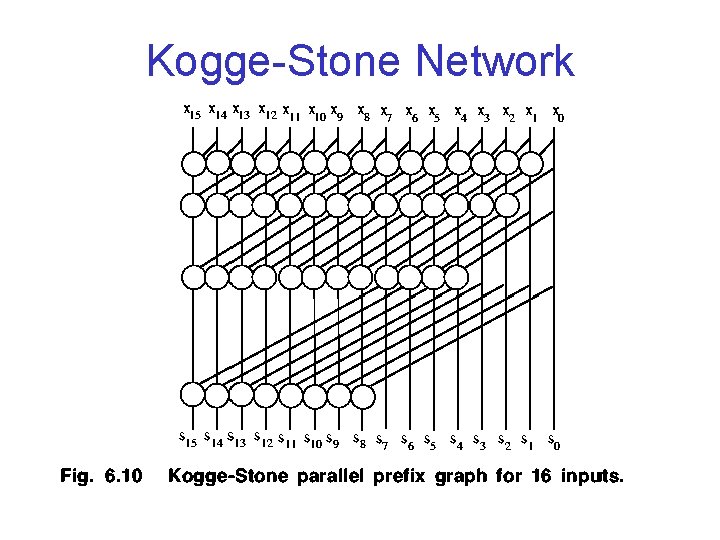
Kogge-Stone Network

Area/Levels of Prefix Networks

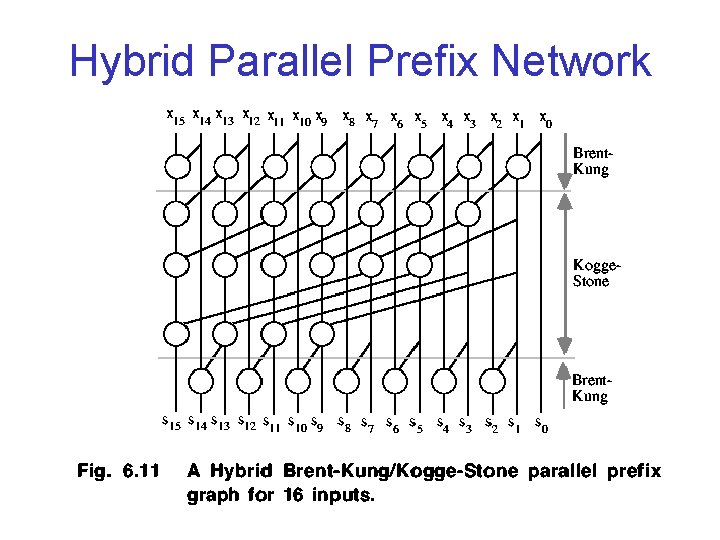
Hybrid Parallel Prefix Network