Recurrence Relations Selected Exercises 10 a A person

Recurrence Relations: Selected Exercises

10 (a) A person deposits $1, 000 in an account that yields 9% interest compounded annually. a) Set up a recurrence relation for the amount in the account at the end of n years. 2

10 (a) Solution Let an represent the amount after n years. an = an-1 + 0. 09 an-1 = 1. 09 an-1 a 0 = 1000. 3

10 (b) A person deposits $1, 000 in an account that yields 9% interest compounded annually. Find an explicit formula for the amount in the account at the end of n years. 4

10 (b) Solution After 1 year, a 1 = 1. 09 a 0 = 1. 09 x 1000 = 1000 x 1. 091 After 2 years, a 2 = 1. 09 a 1 = 1. 09(1000 x(1. 09)1) = 1000 x(1. 09)2 After n years, an = 1000 x(1. 09)n Since an is recursively defined, we prove the formula, for n ≥ 0, by mathematical induction (The problem does not ask for proof). 5

10 (b) Solution Basis n = 0: a 0 = 1000 x(1. 09)0. The 1 st equality is the recurrence relation’s initial condition. Show: an = 1000 x 1. 09 n an+1 = 1000 x 1. 09 n+1. 1. Assume an = 1000 x 1. 09 n. 2. an+1 = 1. 09 an = 1. 09 (1000 x 1. 09 n) = 1000 x 1. 09 n+1. The 1 st equality is from the definition of the recurrence relation. The 2 nd equality is from the induction hypothesis. 6

10 (c) A person deposits $1, 000 in an account that yields 9% interest compounded annually. How much money will the account contain after 100 years? 7

10 (c) Solution The account will contain a 100 dollars after 100 years: a 100 = 1000 x 1. 09100 = $5, 529, 041. That is before taxes . With 30% federal + 10% CA on interest earned, it becomes 1000 x 1. 05100 = $131, 500. 8

20 A country uses as currency: – coins with pesos values of 1, 2, 5, & 10 pesos – bills with pesos values of 5, 10, 20, 50, & 100. Find a recurrence relation, an, for the # of payment sequences for n pesos. E. g. , a bill of 4 pesos could be paid with any of the following sequences: 1. 1, 1, 1, 1 2. 1, 1, 2 3. 1, 2, 1 4. 2, 1, 1 5. 2, 2 9

20 Solution For n pesos, our 1 st (order matters) currency object can be a coin or a bill. Sequences that start w/ a 1 peso coin are different from other sequences: Use the sum principle to decompose this problem into disjoint subproblems, based on which kind of currency object starts the sequence. If the 1 st currency object is a coin, it could be a: • 1 peso coin, in which case we have an-1 ways to finish the bill • 2 peso coin, in which case we have an-2 ways to finish the bill • 5 peso coin, in which case we have an-5 ways to finish the bill • 10 peso coin, in which case we have an-10 ways to finish the bill If there were only coins, the recurrence relation would be an = an-1 + an-2 + an-5 + an-10 with 10 initial conditions, a 1 = 1, a 2 = 2, a 3 = 3, a 4 = 5, a 5 = 9, a 6 = 15, a 7 = 26, a 8 = 44, a 9 = 75, a 10 = 125 10

20 Solution continued But, we also can use bills. If the 1 st currency object is a bill, it could be a 1. 2. 3. 4. 5. 5 peso, in which case we have an-5 ways to finish the bill 10 peso, in which case we have an-10 ways to finish the bill 20 peso, in which case we have an-20 ways to finish the bill 50 peso, in which case we have an-50 ways to finish the bill 100 peso, in which case we have an-100 ways to finish the bill So, using both coins & bills, we have an = an-1 + an-2 + an-5 + an-10 + an-20 + an-50 + an-100 = an-1 + an-2 + 2 an-5 + 2 an-10 + an-20 + an-50 + an-100 , with 100 initial conditions, which I will not produce. 11

30 (a) A string that contains only 0 s, 1 s, & 2 s is called a ternary string. Find a recurrence relation for the # of ternary strings of length n that do not contain 2 consecutive 0 s. 12

30 (a) Solution We subtract the # of “bad” strings, bn, , from the # of ternary strings, 3 n. We use the sum principle to decompose the problem into disjoint subproblems, depending on what digit starts the string: Case the string starts with a 1: bn-1 ways to finish the string. Case the string starts with a 2: bn-1 ways to finish the string. Case the string starts with a 0: Case the remaining string starts with a 0: 3 n-2 ways to finish the string. Case the remaining string starts with a 1: bn-2 ways to finish the string. Case the remaining string starts with a 2: bn-2 ways to finish the string. Summing, bn = 2 bn-1 + 2 bn-2 + 3 n-2 13

30 (b) b) What are the initial conditions? 14

30 (b) Solution b 0 = b 1 = 0. Why do we need 2 initial conditions? 15

30 (c) How many ternary strings of length 6 contain 2 consecutive 0 s? 16

30 (c) Solution The number of such strings is b 6. Using bn = 2 bn-1 + 2 bn-2 + 3 n-2, we compute: b 0 = b 1 = 0. (Initial conditions) b 2 = 2 b 1 + 2 b 0 + 30 = 1 b 3 = 2 b 2 + 2 b 1 + 31 = 2 x 1 + 2 x 0 + 31 = 5 b 4 = 2 b 3 + 2 b 2 + 32 = 2 x 5 + 2 x 1 + 32 = 21 b 5 = 2 b 4 + 2 b 3 + 33 = 2 x 21 + 2 x 5 + 33 = 79 b 6 = 2 b 5 + 2 b 4 + 34 = 2 x 79 + 2 x 21 + 34 = 281. 17

40 Find a recurrence relation, en, for the # of bit strings of length n with an even # of 0 s. 18

40 Solution Strings are sequences: Order matters: There is a 1 st bit. Use the sum principle to decompose the problem into disjoint subproblems, based on their 1 st bit: The strings with an even # of 0 s that begin with 1: en-1 The strings with an even # of 0 s that begin with 0: 2 n-1 - en-1 Summing, en = en-1 + 2 n-1 - en-1 = 2 n-1 Does this answer suggest an alternate explanation? Remember this question when we study binomial coefficients. 19

20

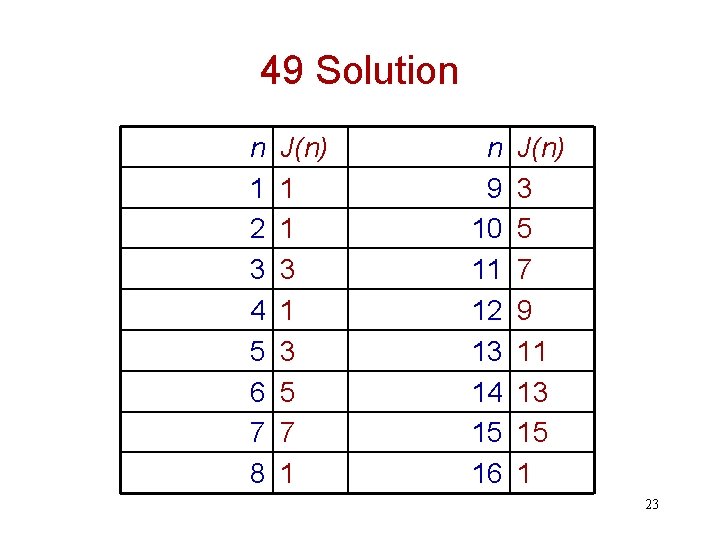
49 The variation we consider begins with people numbered 1, …, n, standing around a circle. In each stage, every 2 nd person still alive is killed until only 1 survives. We denote the number of the survivor by J(n). Determine the value of J(n) for 1 n 16. 21

49 Solution Put 5 people, named 1, 2, 3, 4, & 5, in a circle. Starting with 1, kill every 2 nd person until only 1 person is left. The sequence of killings is: 12345 12345 So, J(5) = 3. Continuing, for each value of n, results in the following table. 22

49 Solution n 1 2 3 4 5 6 7 8 J(n) 1 1 3 5 7 1 n 9 10 11 12 13 14 15 16 J(n) 3 5 7 9 11 13 15 1 23

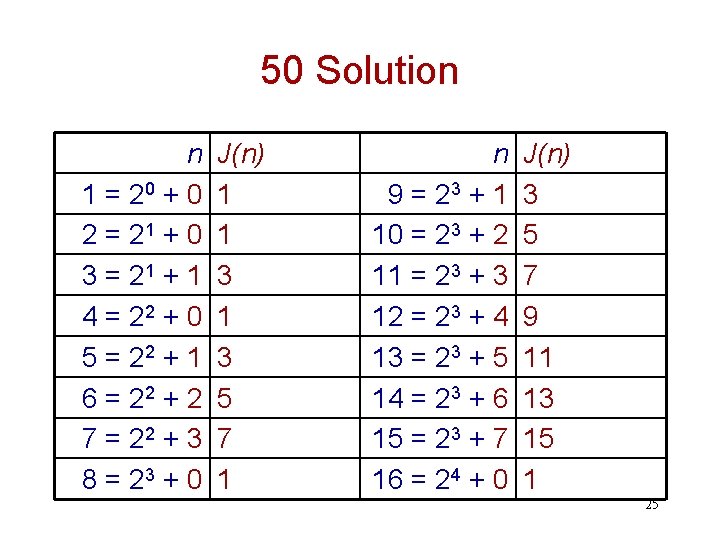
50 Use the values you found in Exercise 49 to conjecture a formula for J(n). Hint: Write n = 2 m + k, where m, k N & k < 2 m. 24

50 Solution n 1 = 20 + 0 2 = 21 + 0 3 = 21 + 1 4 = 22 + 0 5 = 22 + 1 6 = 22 + 2 7 = 22 + 3 8 = 23 + 0 J(n) 1 1 3 5 7 1 n 9 = 23 + 1 10 = 23 + 2 11 = 23 + 3 12 = 23 + 4 13 = 23 + 5 14 = 23 + 6 15 = 23 + 7 16 = 24 + 0 J(n) 3 5 7 9 11 13 15 1 25

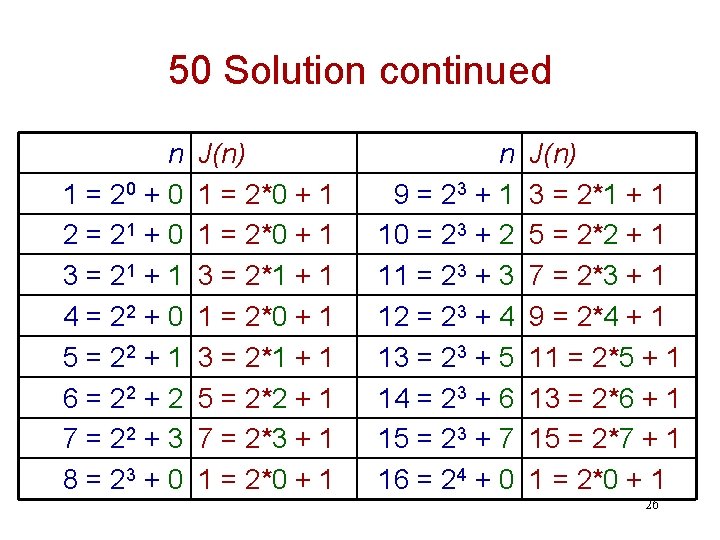
50 Solution continued n 1 = 20 + 0 2 = 21 + 0 3 = 21 + 1 4 = 22 + 0 5 = 22 + 1 6 = 22 + 2 7 = 22 + 3 8 = 23 + 0 J(n) 1 = 2*0 + 1 3 = 2*1 + 1 5 = 2*2 + 1 7 = 2*3 + 1 1 = 2*0 + 1 n 9 = 23 + 1 10 = 23 + 2 11 = 23 + 3 12 = 23 + 4 13 = 23 + 5 14 = 23 + 6 15 = 23 + 7 16 = 24 + 0 J(n) 3 = 2*1 + 1 5 = 2*2 + 1 7 = 2*3 + 1 9 = 2*4 + 1 11 = 2*5 + 1 13 = 2*6 + 1 15 = 2*7 + 1 1 = 2*0 + 1 26

50 Solution continued So, if n = 2 m + k, where m, k N & k < 2 m , then J(n) = 2 k + 1. Check this for J(17). 27