Relations Exercises Exercises In the exercises below take

Relations - Exercises

Exercises In the exercises below take X = { a, b, c, d } Y = { e, f, g } Z = { h, i } In addition, suppose R X Y & R = { (a, e), S X Z & S = { (a, h), T Y Z & T = { (e, h), U Z Z & U = { (h, I) 1. Evaluate a. dom b. ran c. dom d. ran e. dom f. ran g. R~ h. S~ i. T~ j. U~ R R S S T T 2. Evaluate a. R ; T b. T ; R c. S ; T ~ d. R ; R ~ e. (R ; S) ; T ~ f. R ; (S ; T ~) 3. Evaluate a. R S b. S R (a, f), (b, g), (c, e) } (b, h), (c, h), (d, i) } (e, I), (g, h) } }

Exercises 4. In a simple banking system you will have a set of pairs Acc. Balances = { (123, 56. 78), (145, 123. 00), … } Curr. Over = { (222, 200), (234, 500) … } Saving. Accs { (Bill, 123), (Lisa, 145), (Harry, 156), (Sue, 159), (Eve, 154) } S X Z & S = { (a, h), (b, h), (c, h), (d, i) } T Y Z & T = { (e, h), (e, I), (g, h) } a. Write down the type of each of these sets, that is, the sets that each of these are subsets of. b. Would it make any sense to perform the following operations on these sets, or combinations of these sets? • Inverse • Override • Composition c. Evaluate (i) Saving. Accs~ (ii) Savings. Accs ; Acc. Balances

Exercises In the exercises below take R = { (0, 0), (1, 1), (1, 2), (2, 2), (0, 2) } S = { (0, 0), (1, 1), (1, 2), (2, 1), (0, 2) } T = { (0, 0), (0, 1), (0, 2), (1, 0), (2, 0) } 5. 6. Produce a digraph for each relation. Decide whether each of the relations on { 0, 1, 2 } is reflexive, symmetric, transitive or a combination of these and which are equivalence relations.

Problems 1. Let A = {1, 2, 3, 4, 5, 6}. Construct the relation R on A for the following cases. a) R = {(j, k) | j divides k} b) R = {(j, k) | j is a multiple of k} c) R = {(j, k) | (j – k)2 A} d) R = {(j, k) | j/k is a prime} 2. Let R be the relation from A = {1, 2, 3, 4, 5} to B = {1, 3, 5} which is defined by “ x is less than y. ” Write R as a set of ordered pairs. 3. Let R be the relation in the natural numbers N = {1, 2, 3, …. . } defined by “x + 2 y =10”, that is , let R = {(x, y) | x N, y N, x + 2 y = 10}. Find a) the domain and range of R b) R-1
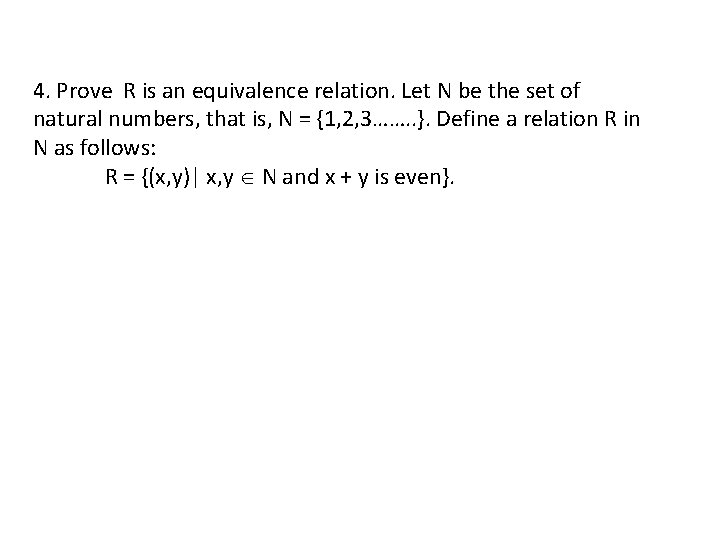
4. Prove R is an equivalence relation. Let N be the set of natural numbers, that is, N = {1, 2, 3……. . }. Define a relation R in N as follows: R = {(x, y)| x, y N and x + y is even}.
- Slides: 6