Chapter 2 Recursion The Mirrors A Recursive Valued

Chapter 2 Recursion: The Mirrors

A Recursive Valued Method: n ! (n 階乘) • Problem – 計算出 n! (以函式 factorial(n) 表示) • factorial(n) 的列舉式定義(可用迴圈完成， 請自己寫寫看) factorial(n) = n * (n-1) * (n-2) * … * 1 for any integer n > 0 factorial(0) = 1 © 2005 Pearson Addison-Wesley. All rights reserved 7

A Recursive Valued Method: The Factorial of n • factorial(n) 的遞迴定義 factorial(n) = 1 if n = 0 = n * factorial(n-1) if n > 0 © 2005 Pearson Addison-Wesley. All rights reserved 8

A Recursive Valued Method: The Factorial of n • 遞迴關係 – 一個新項目的值是利用之前項目的值來產生 的數學公式 – Example factorial(n) = n * [(n-1) * (n-2) * … * 1] = n * factorial(n-1) © 2005 Pearson Addison-Wesley. All rights reserved 9

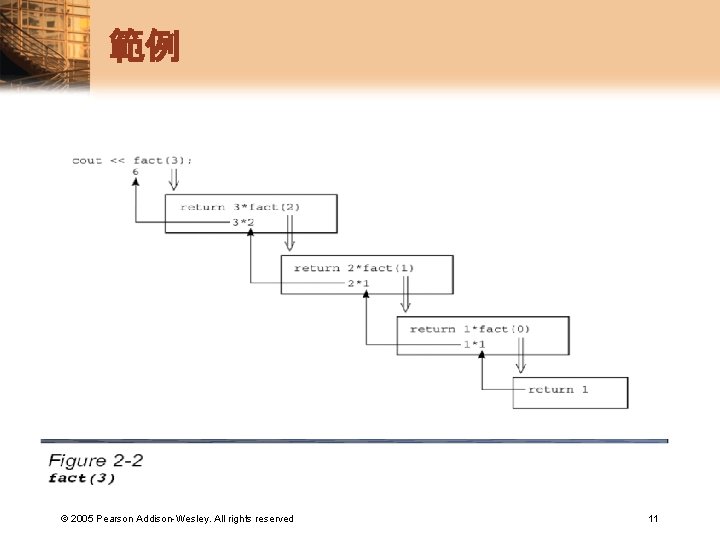
範例 © 2005 Pearson Addison-Wesley. All rights reserved 11

A Recursive Valued Method: The Factorial of n Figure 2. 3 A box © 2005 Pearson Addison-Wesley. All rights reserved 12

A Recursive Valued Method: The Factorial of n © 2005 Pearson Addison-Wesley. All rights reserved 13

A Recursive Valued Method: The Factorial of n © 2005 Pearson Addison-Wesley. All rights reserved 14

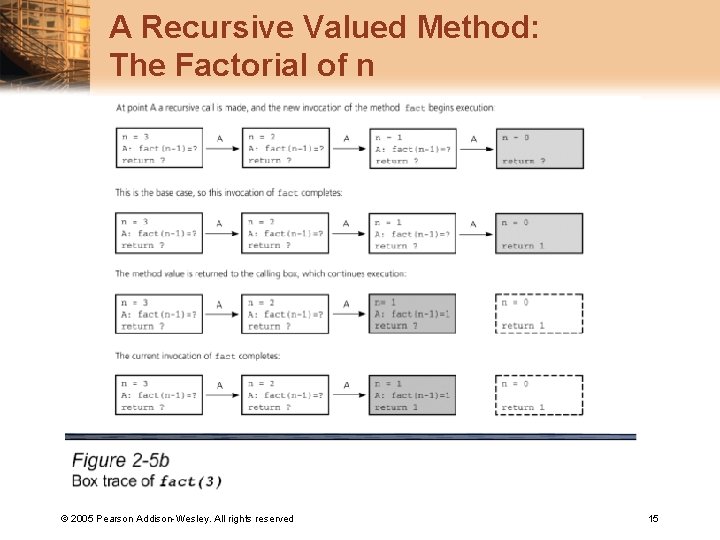
A Recursive Valued Method: The Factorial of n © 2005 Pearson Addison-Wesley. All rights reserved 15

A Recursive Valued Method: The Factorial of n © 2005 Pearson Addison-Wesley. All rights reserved 16

Multiplying Rabbits (The Fibonacci Sequence) • Problem – 在第 n 個月共有幾對兔子? • 遞迴關係 rabbit(n) = rabbit(n-1) + rabbit(n-2) © 2005 Pearson Addison-Wesley. All rights reserved 19

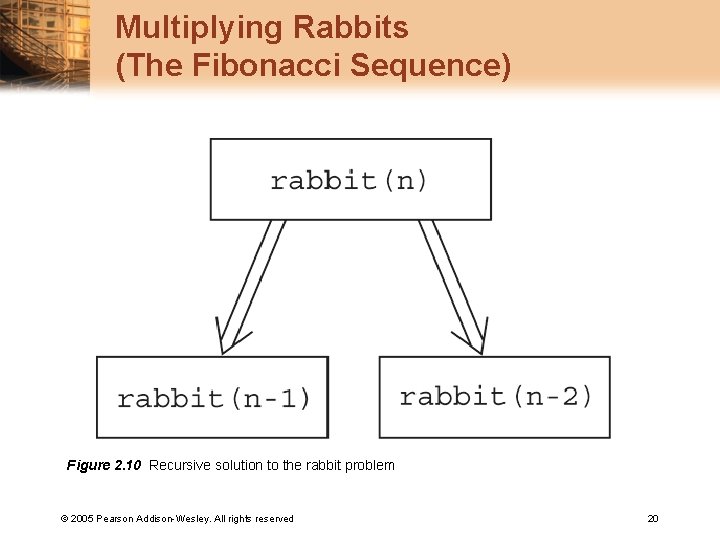
Multiplying Rabbits (The Fibonacci Sequence) Figure 2. 10 Recursive solution to the rabbit problem © 2005 Pearson Addison-Wesley. All rights reserved 20

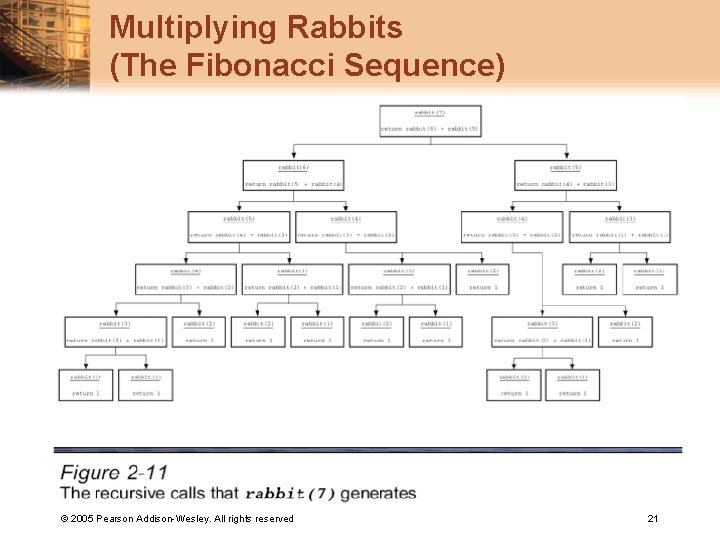
Multiplying Rabbits (The Fibonacci Sequence) © 2005 Pearson Addison-Wesley. All rights reserved 21

Multiplying Rabbits (The Fibonacci Sequence) • 基本狀況 – rabbit(2), rabbit(1) • 遞迴定義 rabbit(n) = 1 if n is 1 or 2 = rabbit(n-1) + rabbit(n-2) if n > 2 • 費氏序列 – 以 rabbit(1), rabbit(2), rabbit(3), … 這些值形 成的序列 © 2005 Pearson Addison-Wesley. All rights reserved 22

Mr. Spock’s Dilemma • 基本狀況 (Choosing k out of n Things) – 自 k 個物件取出 k 個只有一種取法 c(k, k) = 1 – 什麼都不取的取法也只有一種 c(n, 0) = 1 – 無法取出比 n 更多個物件 c(n, k) = 0 if k > n © 2005 Pearson Addison-Wesley. All rights reserved 26

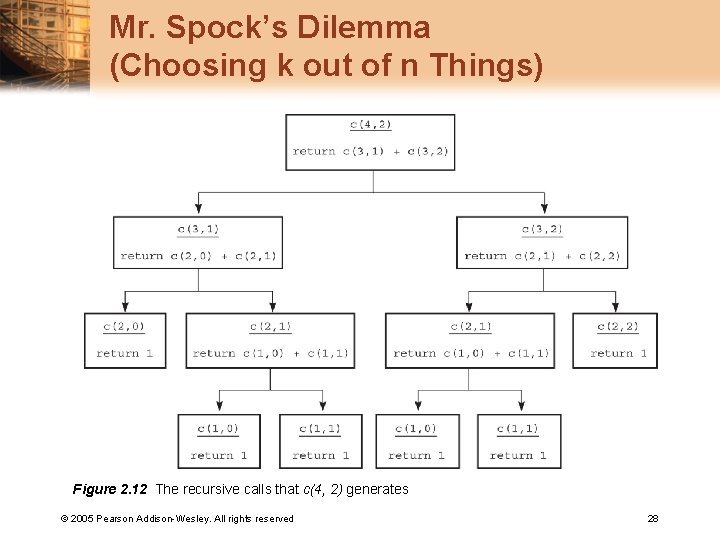
Mr. Spock’s Dilemma (Choosing k out of n Things) • 遞迴定義 c(n, k) = 1 1 0 c(n-1, k-1) + c(n-1, k) © 2005 Pearson Addison-Wesley. All rights reserved if k = 0 if k = n if k > n if 0 < k < n 27

Mr. Spock’s Dilemma (Choosing k out of n Things) Figure 2. 12 The recursive calls that c(4, 2) generates © 2005 Pearson Addison-Wesley. All rights reserved 28

Searching an Array: 找到陣列最大值 • 遞迴解法 if (an. Array 只有一個項目) { max. Array(an. Array) 就是該項目 } else if (an. Array 有不只一個項目) { max. Array(an. Array) 是以下兩數之最大值： max. Array( an. Array 的前面一半陣列) 及 max. Array( an. Array 的後面一半陣列) } // end if © 2005 Pearson Addison-Wesley. All rights reserved 29

Searching an Array: Finding the Largest Item in an Array Figure 2. 13 Recursive solution to the largest-item problem © 2005 Pearson Addison-Wesley. All rights reserved 30

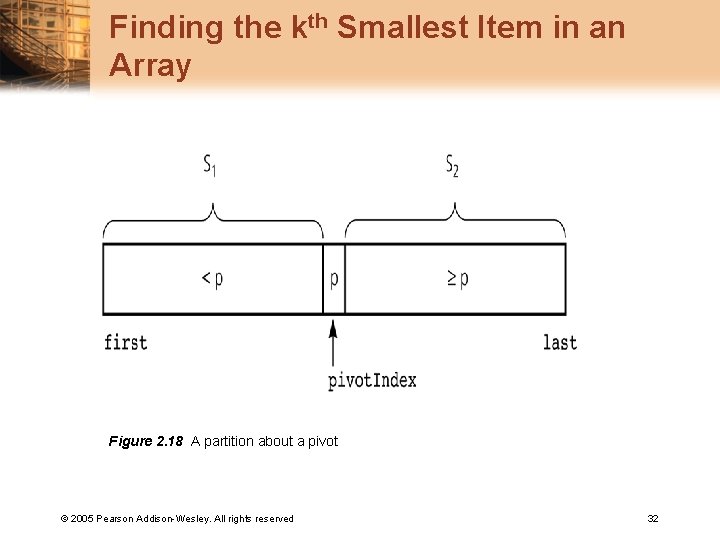
Finding the kth Smallest Item in an Array Figure 2. 18 A partition about a pivot © 2005 Pearson Addison-Wesley. All rights reserved 32

Finding the kth Smallest Item in an Array • Let: k. Small(k, an. Array, first, last) = an. Array[first. . last] 中第 k 個最 小項目 © 2005 Pearson Addison-Wesley. All rights reserved 33

Finding the kth Smallest Item in an Array • 解答(假設陣列已排序): k. Small(k, an. Array, first, last) = k. Small(k, an. Array, first, pivot. Index-1) if k < pivot. Index – first + 1 = p if k = pivot. Index – first + 1 = k. Small(k-(pivot. Index-first+1), an. Array, pivot. Index+1, last) if k > pivot. Index – first + 1 © 2005 Pearson Addison-Wesley. All rights reserved 34

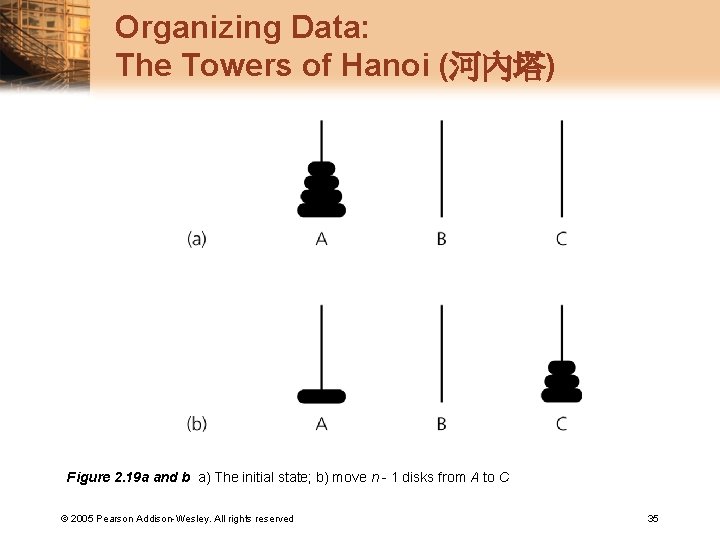
Organizing Data: The Towers of Hanoi (河內塔) Figure 2. 19 a and b a) The initial state; b) move n - 1 disks from A to C © 2005 Pearson Addison-Wesley. All rights reserved 35

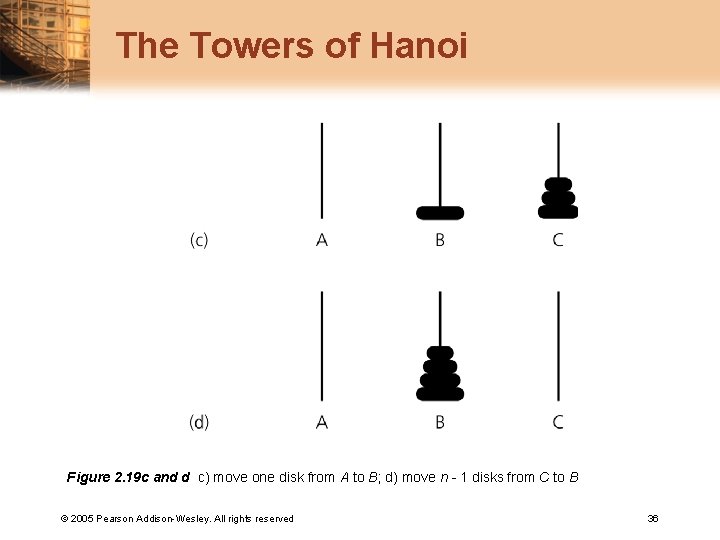
The Towers of Hanoi Figure 2. 19 c and d c) move one disk from A to B; d) move n - 1 disks from C to B © 2005 Pearson Addison-Wesley. All rights reserved 36

The Towers of Hanoi • 擬程式碼 solve. Towers(count, source, destination, spare) if (count is 1) { 直接將盤子由 source 移至 destination } else { solve. Towers(count-1, source, spare, destination) solve. Towers(1, source, destination, spare) solve. Towers(count-1, spare, destination, source) } //end if © 2005 Pearson Addison-Wesley. All rights reserved 37

Summary • Recursion solves a problem by solving a smaller problem of the same type • Four questions: – How can you define the problem in terms of a smaller problem of the same type? – How does each recursive call diminish the size of the problem? – What instance of the problem can serve as the base case? – As the problem size diminishes, will you reach this base case? © 2005 Pearson Addison-Wesley. All rights reserved 40

Summary • A recursive call’s postcondition can be assumed to be true if its precondition is true • The box trace can be used to trace the actions of a recursive method • Recursion can be used to solve problems whose iterative solutions are difficult to conceptualize © 2005 Pearson Addison-Wesley. All rights reserved 41

Summary • Some recursive solutions are much less efficient than a corresponding iterative solution due to their inherently inefficient algorithms and the overhead of method calls • If you can easily, clearly, and efficiently solve a problem by using iteration, you should do so © 2005 Pearson Addison-Wesley. All rights reserved 42