Recurrence Relations Divide and conquer is a very

Recurrence Relations • Divide and conquer is a very common problem solving strategy in computer science • Recursion, where you solve a simpler version of the same problem, is a common application of divide and conquer – the recursion “bottoms out” in a base case – Merge sort divides a problem in “half” and solves each half separately – The recurrence relation is – Binary search divides a problem in half but only has to solve the problem for one of the two halves

Common Ways to Solve Recurrence Relations • There are several common ways to solve a recurrence relation – The substitution method (guess and then check) – The recurrence tree method (sum up complexity at each level, then sum all the levels) – The master method (prove a general theorem once then apply theorem where appropriate; covers many common cases but not all cases) – Generating functions (only introduced in exercise 4 -5 in this textbook; we will not cover it in class)

The Substitution Method - 1 • Given the recurrence – This is the recurrence for a merge sort – Intuitively we know each pass of a merge sort has complexity O(n) (why? ) and there are O(log n) passes (why? ) – So we guess the correct solution is O(n log n) – we verify this by using mathematical induction

The Substitution Method - 2 • Our inductive assumption is • This is true for any c 1

The Substitution Method - 3 • Our induction must hold for the base case too • Using our formula we find T(1) c * 1 * lg 1 = 0 which does not agree with T(1) = 1 • Remember our asymptotic assumption only requires we find an n n 0 for which to formula holds, so selecting n 0 > 1 eliminates the “bad” base case

Some Subtleties - 1 • Given the recurrence • A reasonable guess would be O(n) • But there is no c such that T(n) c n • We are only using weak induction where we assume it is only true for the prior value; we need to use strong induction (it is true for all prior values)

Some Subtleties - 2 • We subtract a lower order term, call it b T(n) <= c n – b and now substitute in our solution • This works provided b >= 1 • We can then prove our boundary condition for c

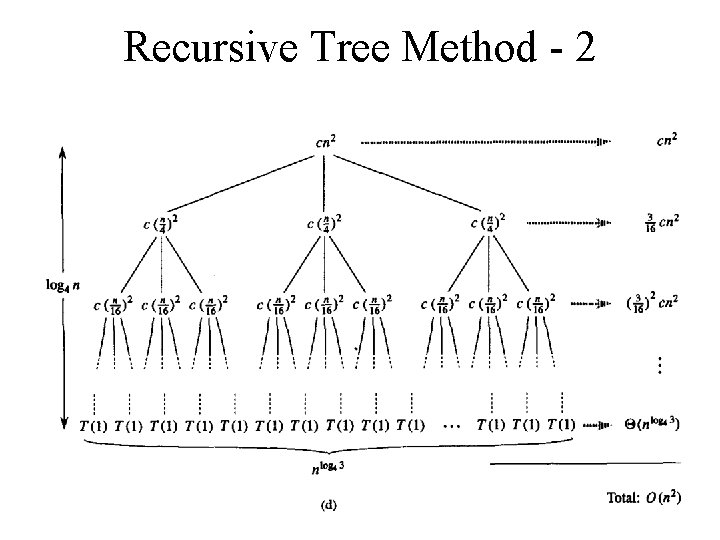
Recursive Tree Method - 1 • Given the recurrence T(n) = 3 T(n/4) + c n 2 • Expanding the first couple levels of the tree

Recursive Tree Method - 2

Recursive Tree Method - 3 • We find the total cost for each level of the tree • We then add up the costs for all levels • This appears to be the formula for a decreasing geometric series

Recursive Tree Method - 4 • In general we have (A. 6)

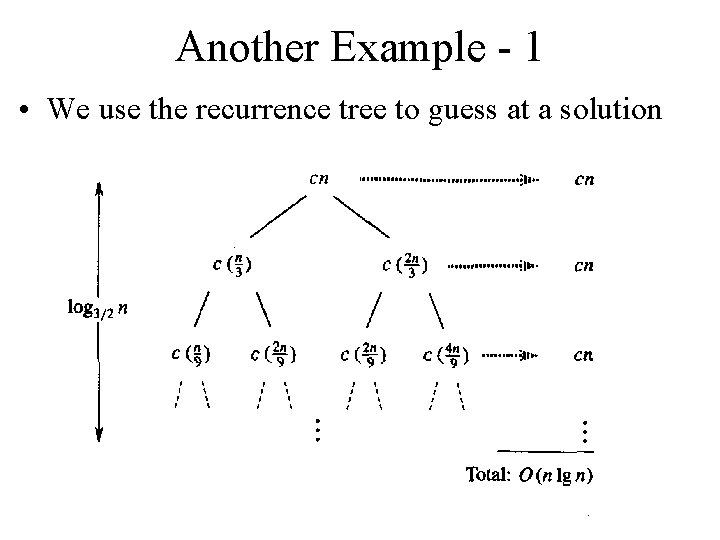
Another Example - 1 • We use the recurrence tree to guess at a solution

Another Example - 2 • We now verify by substitution • It is a common strategy to use the recurrence tree method to guess a solution and then to verify the solution by substitution

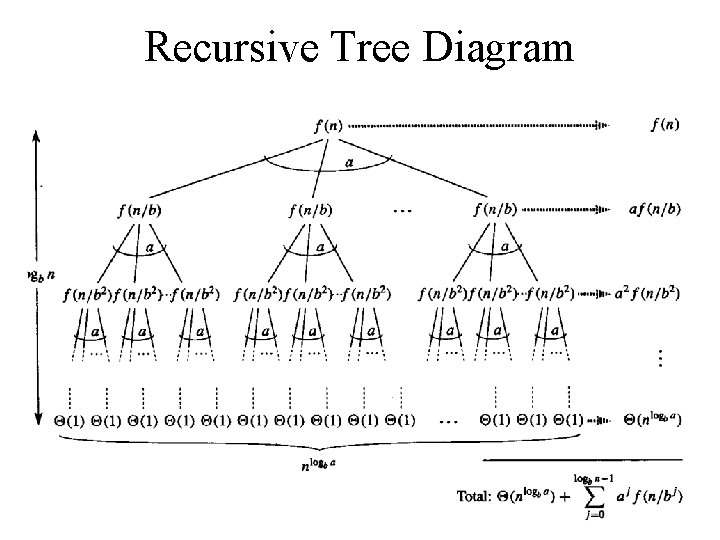
The Master Method • The book provides a rigorous proof; we only suggest a proof by the tree diagram on the next page

Recursive Tree Diagram

Examples • First example • Second example