Adversarial Machine Learning Daniel Lowd University of Oregon

Adversarial Machine Learning Daniel Lowd, University of Oregon Christopher Meek, Microsoft Research Pedro Domingos, University of Washington

Motivation n Many adversarial problems ¨ Spam filtering ¨ Malware detection ¨ Worm detection ¨ New ones every year! n n Want general-purpose solutions We can gain much insight by modeling adversarial situations mathematically

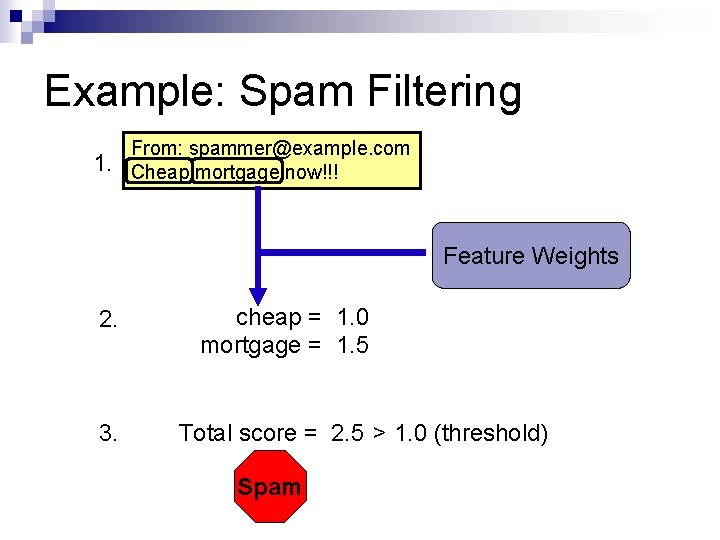
Example: Spam Filtering 1. From: spammer@example. com Cheap mortgage now!!! Feature Weights 2. 3. cheap = 1. 0 mortgage = 1. 5 Total score = 2. 5 > 1. 0 (threshold) Spam

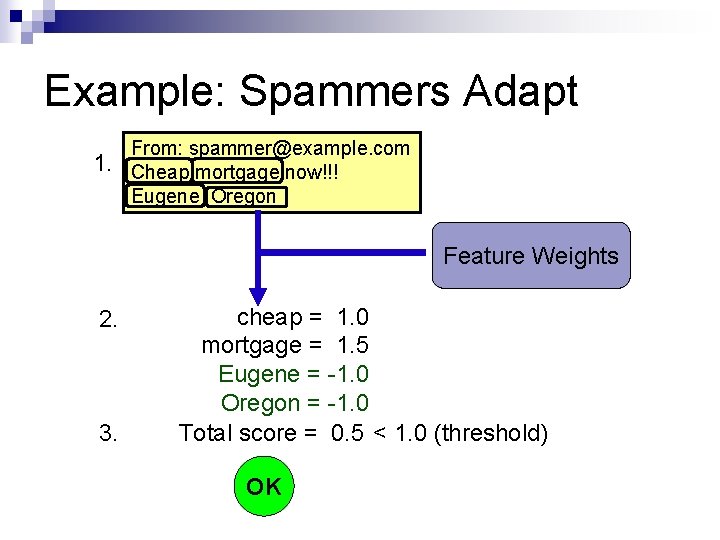
Example: Spammers Adapt 1. From: spammer@example. com Cheap mortgage now!!! Eugene Oregon Feature Weights 2. 3. cheap = 1. 0 mortgage = 1. 5 Eugene = -1. 0 Oregon = -1. 0 Total score = 0. 5 < 1. 0 (threshold) OK

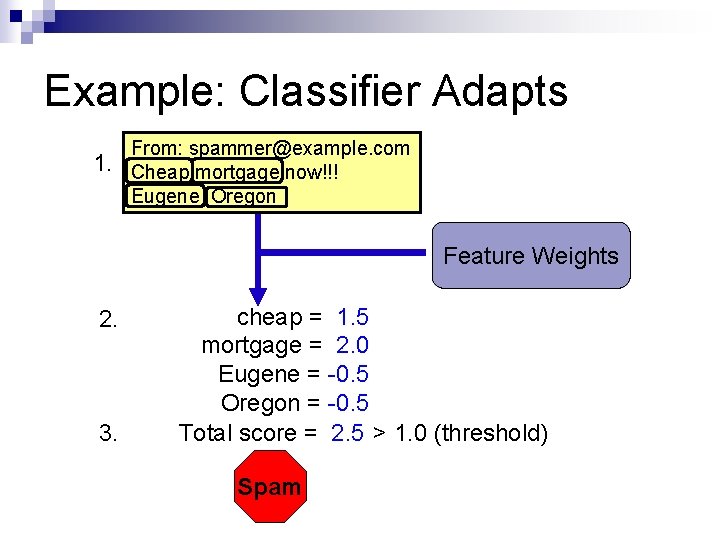
Example: Classifier Adapts 1. From: spammer@example. com Cheap mortgage now!!! Eugene Oregon Feature Weights 2. 3. cheap = 1. 5 mortgage = 2. 0 Eugene = -0. 5 Oregon = -0. 5 Total score = 2. 5 > 1. 0 (threshold) Spam OK

Outline n n Problem definitions Anticipating adversaries ¨ ¨ ¨ n n Goal: Defeat adaptive adversary Assume: Perfect information, optimal short-term strategies Results: Vastly better classifier accuracy Reverse engineering classifiers ¨ ¨ (Dalvi et al. , 2004) (Lowd & Meek, 2005 a, b) Goal: Assess classifier vulnerability Assume: Membership queries from adversary Results: Theoretical bounds, practical attacks Also: How to defeat a spam filter with 30 words or less! Conclusion

Definitions Instance space Adversarial cost function Classifier - X 2 x X 2 + X 1 X = {X 1, X 2, …, Xn} Each Xi is a feature (e. g. , a word) Instances, x X (e. g. , emails) X 1 c(x): X {+, } c C, concept class (e. g. , linear classifier) X 1 a(x): X R a A (e. g. , more legible spam is better)

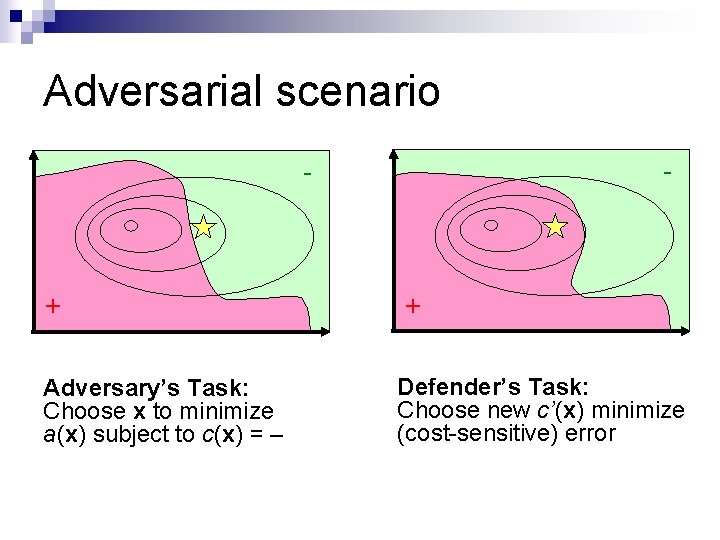
Adversarial scenario - - + Adversary’s Task: Choose x to minimize a(x) subject to c(x) = + Defender’s Task: Choose new c’(x) minimize (cost-sensitive) error

Cost-sensitive error: Not all errors are equal! “Better that ten guilty persons escape than that one innocent suffer. ” -- William Blackstone, 1760 False Positive Rate (FP): Fraction of “good” instances misclassified as “bad” (e. g. , good email blocked by filter) False Negative Rate (FN): Fraction of “bad” instances misclassified as “good” (e. g. , spam that gets through) Classifier Utility: UC = 1 – c. FP FP – c. FN FN

This is a game! n n n Adversary’s actions: {x X} Defender’s actions: {c C} Assume perfect information Finding a Nash equilibrium is triply exponential (at best)! Instead, we’ll look at optimal myopic strategies: Best action assuming nothing else changes

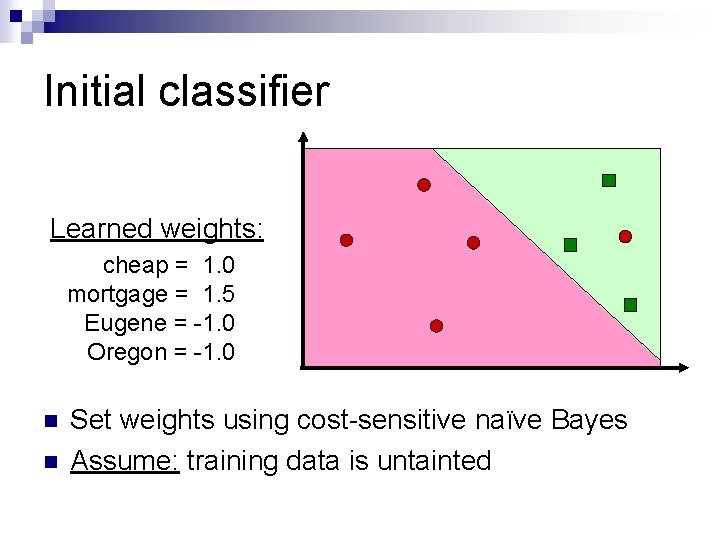
Initial classifier Learned weights: cheap = 1. 0 mortgage = 1. 5 Eugene = -1. 0 Oregon = -1. 0 n n Set weights using cost-sensitive naïve Bayes Assume: training data is untainted

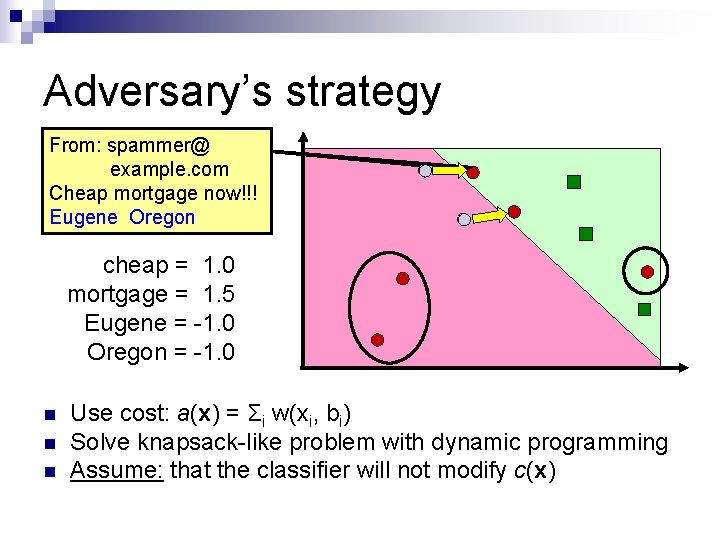
Adversary’s strategy From: spammer@ example. com Cheap mortgage now!!! Eugene Oregon cheap = 1. 0 mortgage = 1. 5 Eugene = -1. 0 Oregon = -1. 0 n n n Use cost: a(x) = Σi w(xi, bi) Solve knapsack-like problem with dynamic programming Assume: that the classifier will not modify c(x)

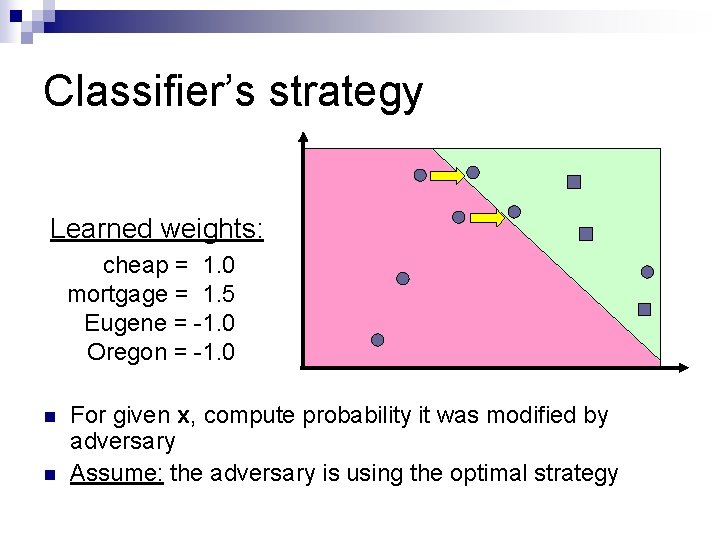
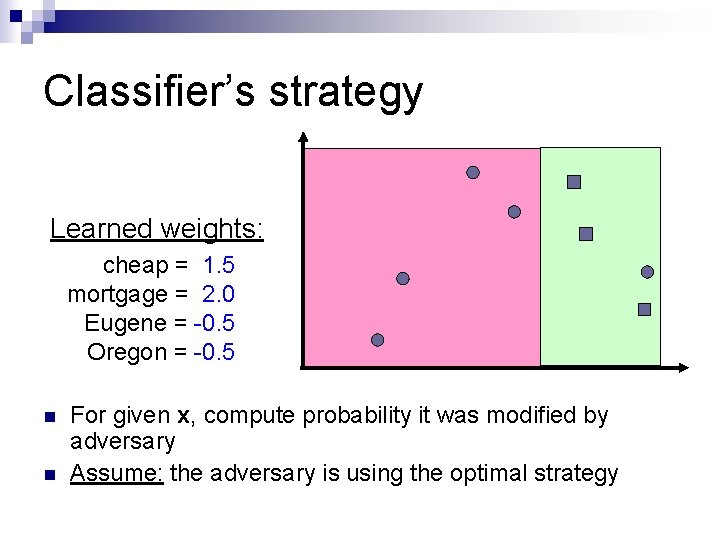
Classifier’s strategy Learned weights: cheap = 1. 0 mortgage = 1. 5 Eugene = -1. 0 Oregon = -1. 0 n n For given x, compute probability it was modified by adversary Assume: the adversary is using the optimal strategy

Classifier’s strategy Learned weights: cheap = 1. 5 mortgage = 2. 0 Eugene = -0. 5 Oregon = -0. 5 n n For given x, compute probability it was modified by adversary Assume: the adversary is using the optimal strategy

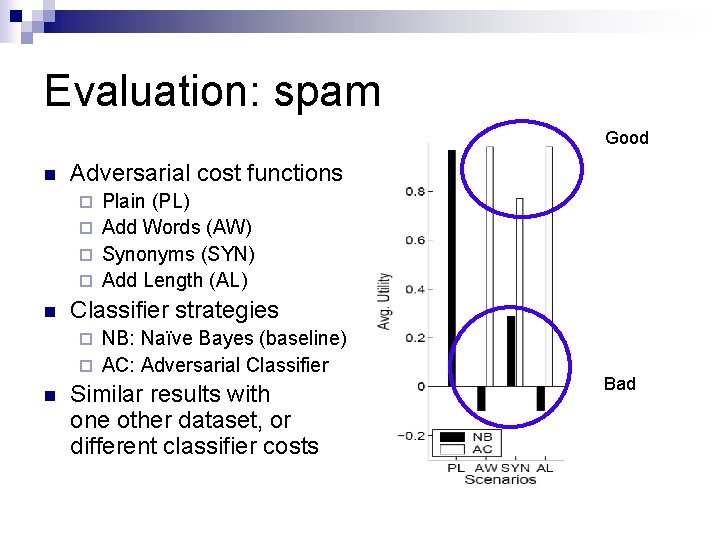
Evaluation: spam Good n Adversarial cost functions Plain (PL) ¨ Add Words (AW) ¨ Synonyms (SYN) ¨ Add Length (AL) ¨ n Classifier strategies NB: Naïve Bayes (baseline) ¨ AC: Adversarial Classifier ¨ n Similar results with one other dataset, or different classifier costs Bad

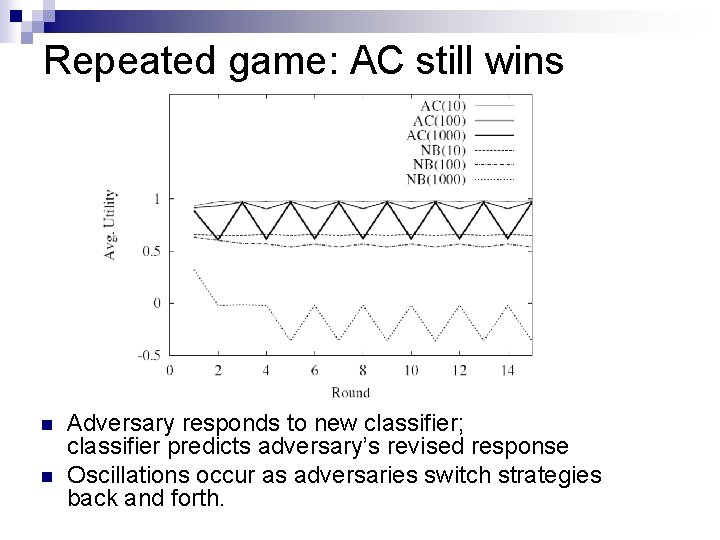
Repeated game: AC still wins n n Adversary responds to new classifier; classifier predicts adversary’s revised response Oscillations occur as adversaries switch strategies back and forth.

Outline n n Problem definitions Anticipating adversaries ¨ ¨ ¨ n n Goal: Defeat adaptive adversary Assume: Perfect information, optimal short-term strategies Results: Vastly better classifier accuracy Reverse engineering classifiers ¨ ¨ (Dalvi et al. , 2004) (Lowd & Meek, 2005 a, b) Goal: Assess classifier vulnerability Assume: Membership queries from adversary Results: Theoretical bounds, practical attacks Also: How to defeat a spam filter with 30 words or less! Conclusion

Imperfect information n n What can an adversary accomplish with limited knowledge of the classifier? Goals: ¨ Understand classifier’s vulnerabilities ¨ Understand our adversary’s likely strategies “If you know the enemy and know yourself, you need not fear the result of a hundred battles. ” -- Sun Tzu, 500 BC

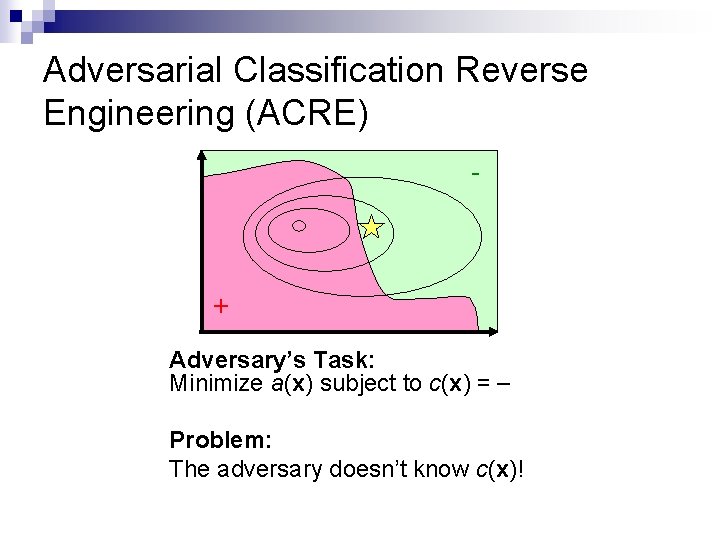
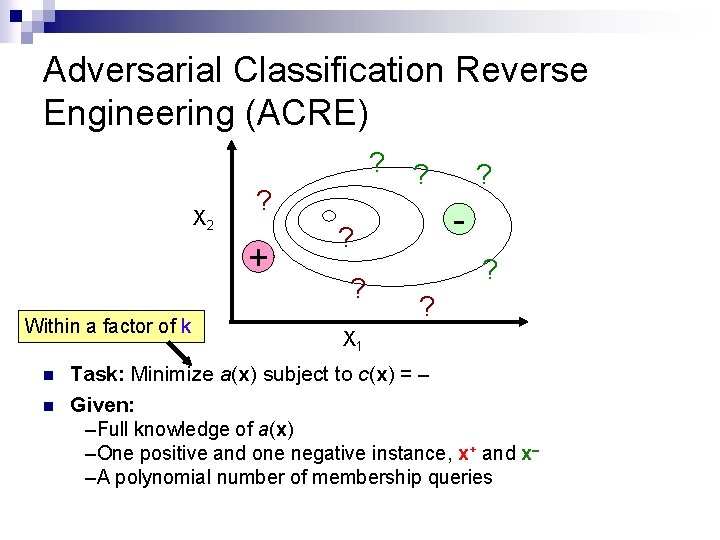
Adversarial Classification Reverse Engineering (ACRE) - + Adversary’s Task: Minimize a(x) subject to c(x) = Problem: The adversary doesn’t know c(x)!

Adversarial Classification Reverse Engineering (ACRE) ? X 2 ? + Within a factor of k n n ? - ? ? ? X 1 Task: Minimize a(x) subject to c(x) = Given: –Full knowledge of a(x) –One positive and one negative instance, x+ and x –A polynomial number of membership queries

Comparison to other theoretical learning methods Probably Approximately Correct (PAC): accuracy over same distribution n Membership queries: exact classifier n ACRE: single low-cost, negative instance n

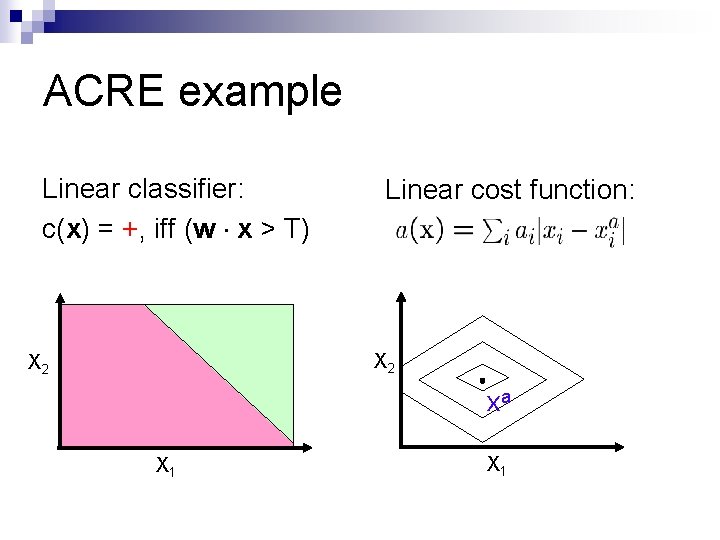
ACRE example Linear classifier: c(x) = +, iff (w x > T) Linear cost function: X 2 xa X 1

Linear classifiers with continuous features n n ACRE learnable within a factor of (1+ ) under linear cost functions Proof sketch Only need to change the highest weight/cost feature ¨ We can efficiently find this feature using line searches in each dimension ¨ X 2 xa X 1

Linear classifiers with Boolean features Harder problem: can’t do line searches n ACRE learnable within a factor of 2 if adversary has unit cost per change: n c(x) x- xa wi wj wk wl wm

Algorithm Iteratively reduce the cost in two ways: 1. Remove any unnecessary change: O(n) c(x) 2. xa y wi wj wk xwm wl Replace any two changes with one: O(n 3) c(x) xa y’ wi wj wk wl wp

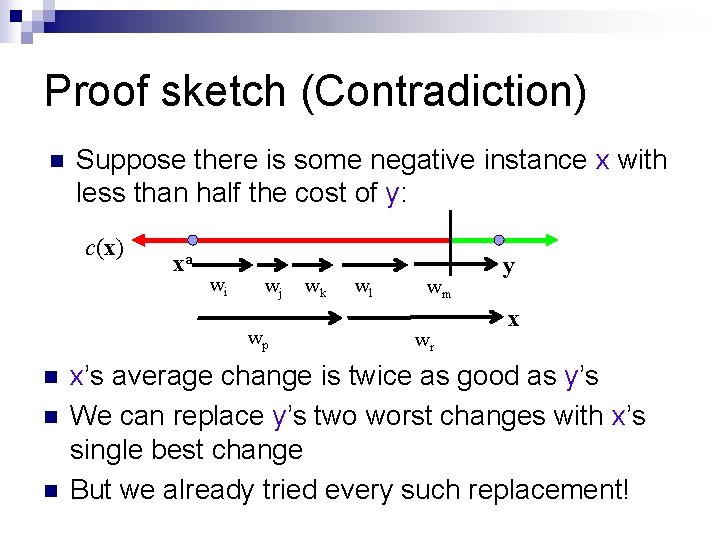
Proof sketch (Contradiction) n Suppose there is some negative instance x with less than half the cost of y: c(x) xa wi wj wp n n n wk wl wm wr y x x’s average change is twice as good as y’s We can replace y’s two worst changes with x’s single best change But we already tried every such replacement!

Evaluation: Is O(n 3) practical? n n n Classifiers: Naïve Bayes (NB), Maxent (ME) Data: 500 k Hotmail messages, 276 k features Adversary feature sets: 23, 000 words (Dict) ¨ 1, 000 random words (Rand) ¨ Dict NB Dict ME Rand NB Cost 23 10 31 Rand ME 12 Queries 261, 000 119, 000 23, 000 Answer: Yes 9, 000

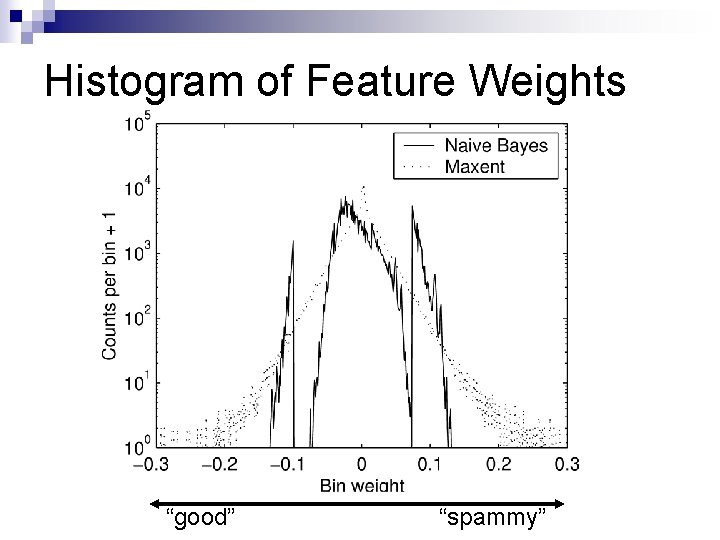
Histogram of Feature Weights “good” “spammy”

Finding features We can find good features (words) instead of good instances (emails) n Active attacks: Test emails allowed n Passive attacks: No filter access n

Active Attacks Learn which words are best by sending test messages (queries) through the filter n First-N: Find n good words using as few queries as possible n Best-N: Find the best n words n

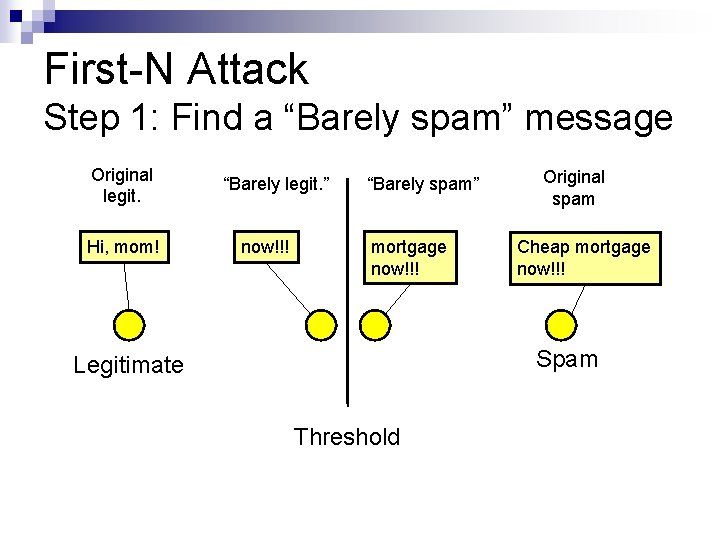
First-N Attack Step 1: Find a “Barely spam” message Original legit. Hi, mom! “Barely legit. ” now!!! “Barely spam” mortgage now!!! Original spam Cheap mortgage now!!! Spam Legitimate Threshold

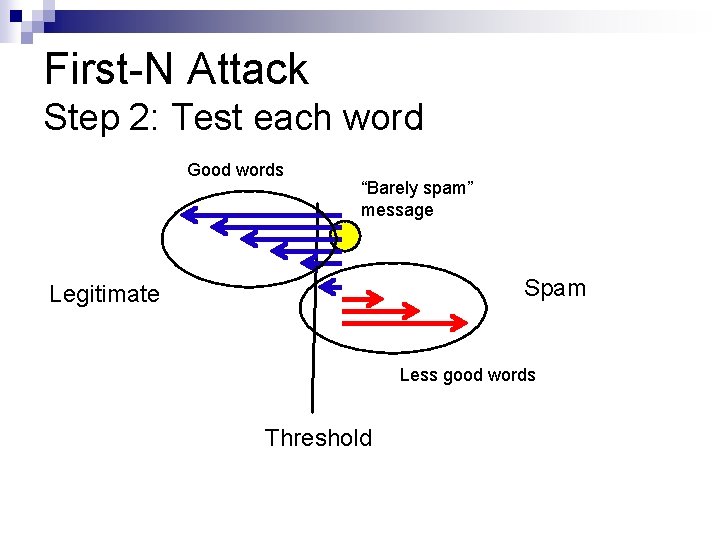
First-N Attack Step 2: Test each word Good words “Barely spam” message Spam Legitimate Less good words Threshold

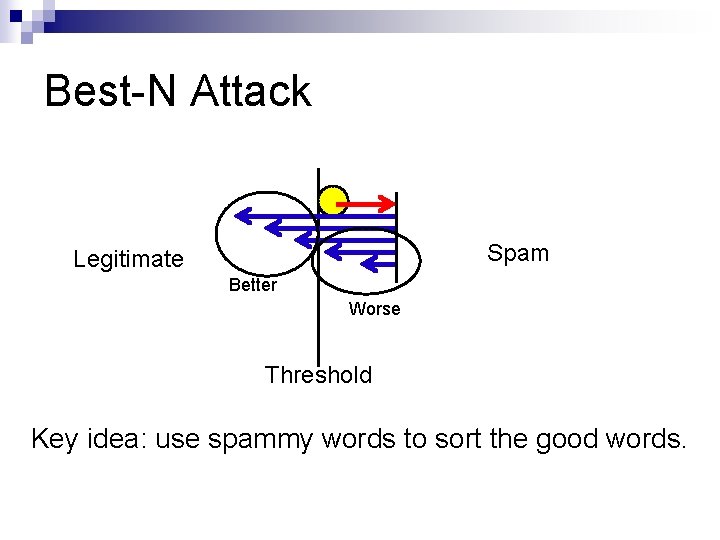
Best-N Attack Spam Legitimate Better Worse Threshold Key idea: use spammy words to sort the good words.

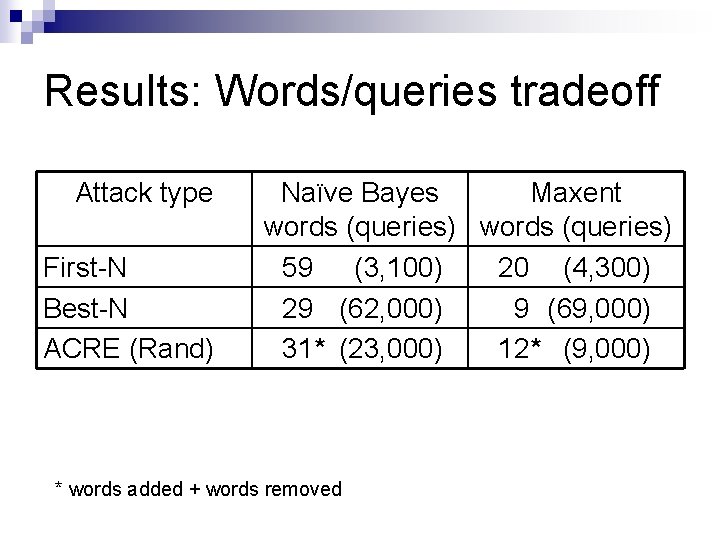
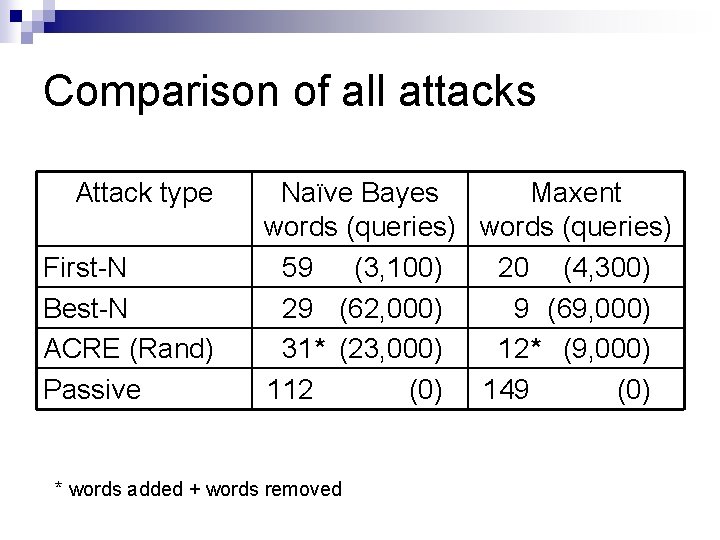
Results: Words/queries tradeoff Attack type First-N Best-N ACRE (Rand) Naïve Bayes Maxent words (queries) 59 (3, 100) 20 (4, 300) 29 (62, 000) 9 (69, 000) 31* (23, 000) 12* (9, 000) * words added + words removed

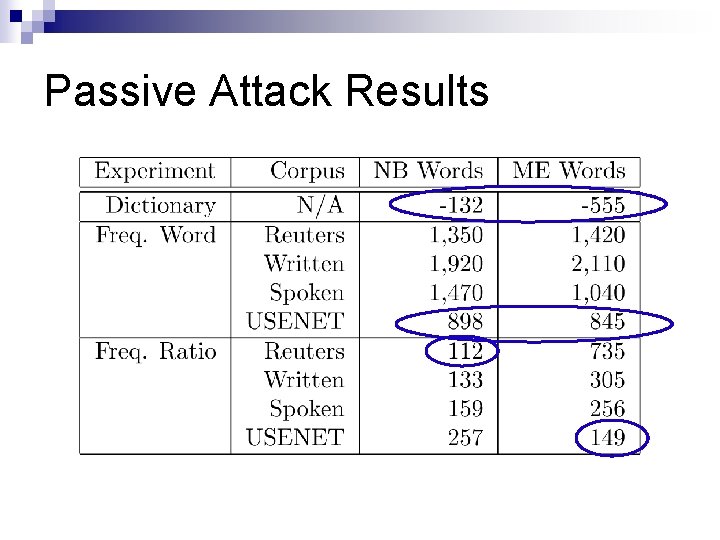
Passive Attacks n Heuristics Select random dictionary words (Dictionary) ¨ Select most frequent English words (Freq. Word) ¨ Select highest ratio: English freq. /spam freq. (Freq. Ratio) ¨ n n Spam corpus: spamarchive. org English corpora: Reuters news articles ¨ Written English ¨ Spoken English ¨ 1992 USENET ¨

Passive Attack Results

Comparison of all attacks Attack type First-N Best-N ACRE (Rand) Passive Naïve Bayes Maxent words (queries) 59 (3, 100) 20 (4, 300) 29 (62, 000) 9 (69, 000) 31* (23, 000) 12* (9, 000) 112 (0) 149 (0) * words added + words removed

Conclusion n Mathematical modeling is a powerful tool in adversarial situations ¨ Game theory lets us make classifiers aware of and resistant to adversaries ¨ Complexity arguments let us explore the vulnerabilities of our own systems n This is only the beginning… ¨ Can we weaken our assumptions? ¨ Can we expand our scenarios?

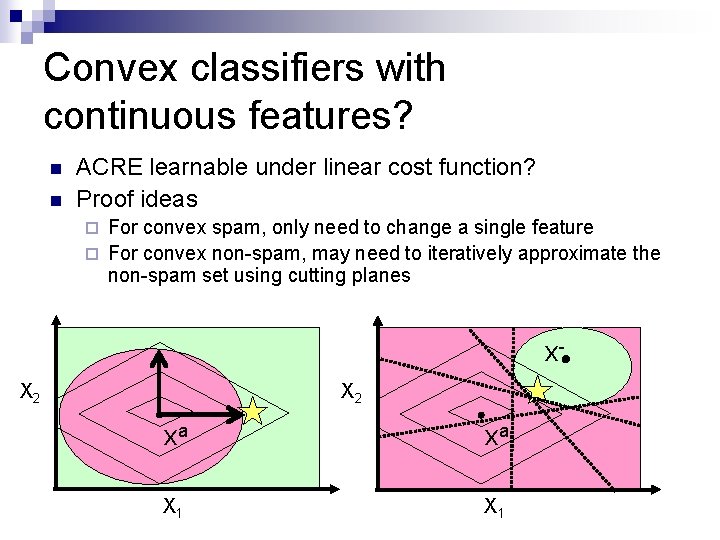
Convex classifiers with continuous features? n n ACRE learnable under linear cost function? Proof ideas For convex spam, only need to change a single feature ¨ For convex non-spam, may need to iteratively approximate the non-spam set using cutting planes ¨ x. X 2 xa xa X 1

Conclusion n Mathematical modeling is a powerful tool in adversarial situations ¨ Game theory lets us make classifiers aware of and resistant to adversaries ¨ Complexity arguments let us explore the vulnerabilities of our own systems n This is only the beginning… ¨ Can we weaken our assumptions? ¨ Can we expand our scenarios?

Example: Trivial cost function X 2 - + X 1 n n n Suppose a small, constant number of instances have cost a(x) = b, and all others have cost a(x) = b’, where b’ > b Test each of the b-cost instances If none is negative, choose x

Example: Boolean conjunctions n n Suppose c is a conjunction of Boolean literals (e. g. , x 1 x 3) Starting with x+, toggle each xi in turn: x+ = (x 1 = T, x 2 = F, x 3 = F, x 4 = T) Guess: (x 1 x 2 x 3 x 4)

Example: Boolean conjunctions n n Suppose c is a conjunction of Boolean literals (e. g. , x 1 x 3) Starting with x+, toggle each xi in turn: x+ = (T, F, F, T) Guess: (x 1 x 2 x 3 x 4)

Example: Boolean conjunctions n n Suppose c is a conjunction of Boolean literals (e. g. , x 1 x 3) Starting with x+, toggle each xi in turn: x+ = (T, F, F, T) x’ = (F, F, F, T) c(x’) = Guess: (x 1 x 2 x 3 x 4)

Example: Boolean conjunctions n n Suppose c is a conjunction of Boolean literals (e. g. , x 1 x 3) Starting with x+, toggle each xi in turn: x+ = (T, F, F, T) x’ = (T, T, F, T) c(x’) = + Guess: (x 1 x 2 x 3 x 4)

Example: Boolean conjunctions n n Suppose c is a conjunction of Boolean literals (e. g. , x 1 x 3) Starting with x+, toggle each xi in turn: x+ = (T, F, F, T) x’ = (T, F, T, T) c(x’) = Guess: (x 1 x 2 x 3 x 4)

Example: Boolean conjunctions n n Suppose c is a conjunction of Boolean literals (e. g. , x 1 x 3) Starting with x+, toggle each xi in turn: x+ = (T, F, F, T) x’ = (T, F, F, F) c(x’) = Guess: (x 1 x 2 x 3 x 4) Final Answer: (x 1 x 3)

Example: Boolean conjunctions n n n Suppose c is a conjunction of Boolean literals (e. g. , x 1 x 3) Starting with x+, toggle each xi in turn Exact conjunction is learnable in n queries. Now we can optimize any cost function. In general: concepts learnable with membership queries are ACRE 1 -learnable