Machine Learning Decision Trees Overfitting Reading Mitchell Chapter



![Learning to Predict Emergency C-Sections [Sims et al. , 2000] 9714 patient records, each Learning to Predict Emergency C-Sections [Sims et al. , 2000] 9714 patient records, each](https://slidetodoc.com/presentation_image_h/794c28b6def3f22e99a24390e207fef8/image-4.jpg)

![Reading a noun (vs verb) [Rustandi et al. , 2005] Reading a noun (vs verb) [Rustandi et al. , 2005]](https://slidetodoc.com/presentation_image_h/794c28b6def3f22e99a24390e207fef8/image-7.jpg)



![[ID 3, C 4. 5, …] node = Root [ID 3, C 4. 5, …] node = Root](https://slidetodoc.com/presentation_image_h/794c28b6def3f22e99a24390e207fef8/image-15.jpg)
















- Slides: 40

Machine Learning, Decision Trees, Overfitting Reading: Mitchell, Chapter 3 Machine Learning 10 -601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University January 14, 2008

Machine Learning 10 -601 Instructors • William Cohen • Tom Mitchell TA’s • Andrew Arnold • Mary Mc. Glohon See webpage for • Office hours • Grading policy • Final exam date • Late homework policy • Syllabus details • . . . Course assistant • Sharon Cavlovich webpage: www. cs. cmu. edu/~tom/10601

Machine Learning: Study of algorithms that • improve their performance P • at some task T • with experience E well-defined learning task: <P, T, E>
![Learning to Predict Emergency CSections Sims et al 2000 9714 patient records each Learning to Predict Emergency C-Sections [Sims et al. , 2000] 9714 patient records, each](https://slidetodoc.com/presentation_image_h/794c28b6def3f22e99a24390e207fef8/image-4.jpg)
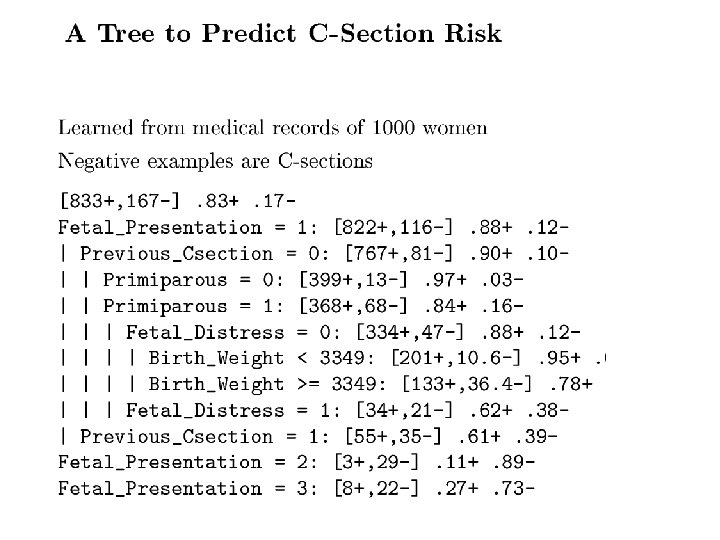
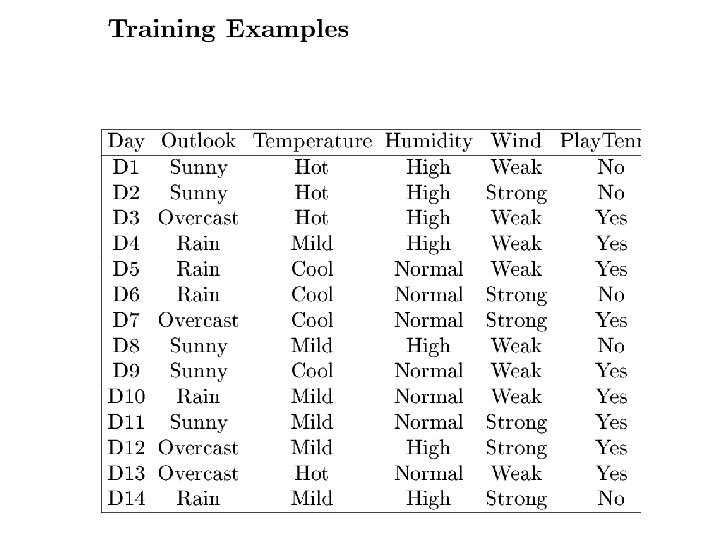
Learning to Predict Emergency C-Sections [Sims et al. , 2000] 9714 patient records, each with 215 features

Learning to detect objects in images (Prof. H. Schneiderman) Example training images for each orientation

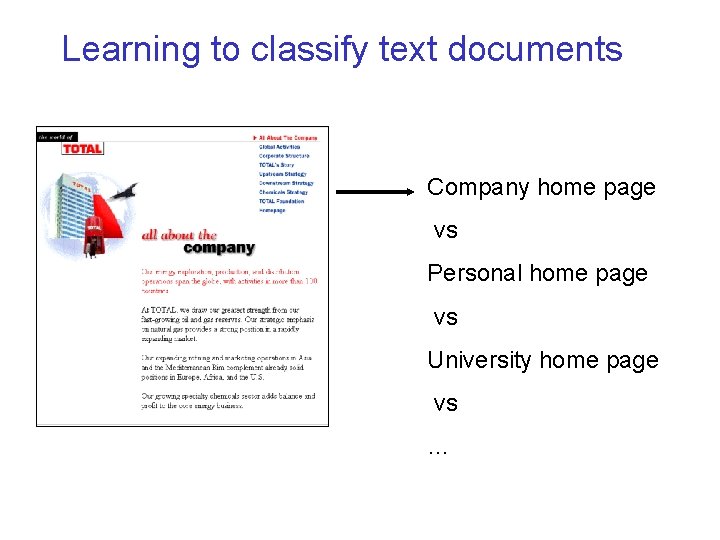
Learning to classify text documents Company home page vs Personal home page vs University home page vs …
![Reading a noun vs verb Rustandi et al 2005 Reading a noun (vs verb) [Rustandi et al. , 2005]](https://slidetodoc.com/presentation_image_h/794c28b6def3f22e99a24390e207fef8/image-7.jpg)
Reading a noun (vs verb) [Rustandi et al. , 2005]

Machine Learning - Practice Speech Recognition Object recognition Mining Databases • Supervised learning Text analysis Control learning • Bayesian networks • Hidden Markov models • Unsupervised clustering • Reinforcement learning • . .

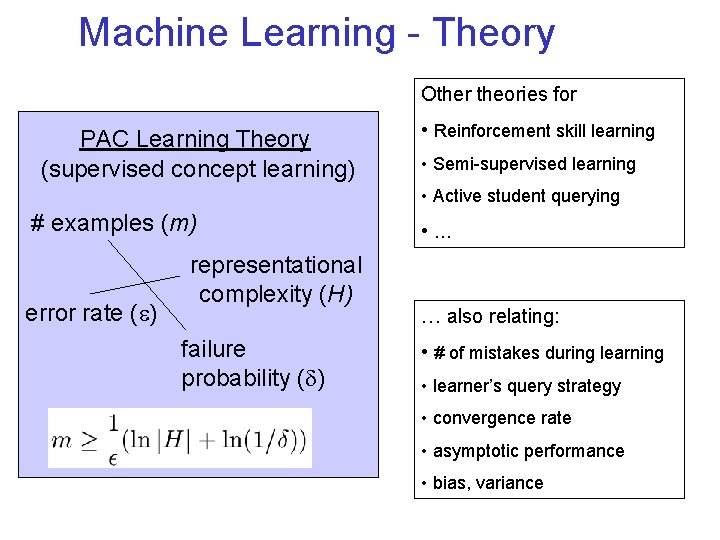
Machine Learning - Theory Other theories for PAC Learning Theory (supervised concept learning) • Reinforcement skill learning • Semi-supervised learning • Active student querying # examples (m) error rate (e) representational complexity (H) failure probability (d) • … … also relating: • # of mistakes during learning • learner’s query strategy • convergence rate • asymptotic performance • bias, variance

Growth of Machine Learning • Machine learning already the preferred approach to – – – Speech recognition, Natural language processing Computer vision Medical outcomes analysis Robot control ML apps. … All software apps. • This ML niche is growing – – – Improved machine learning algorithms Increased data capture, networking Software too complex to write by hand New sensors / IO devices Demand for self-customization to user, environment

Function Approximation and Decision tree learning

Function approximation Setting: • Set of possible instances X • Unknown target function f: X Y • Set of function hypotheses H={ h | h: X Y } Given: • Training examples {<xi, yi>} of unknown target function f Determine: • Hypothesis h H that best approximates f

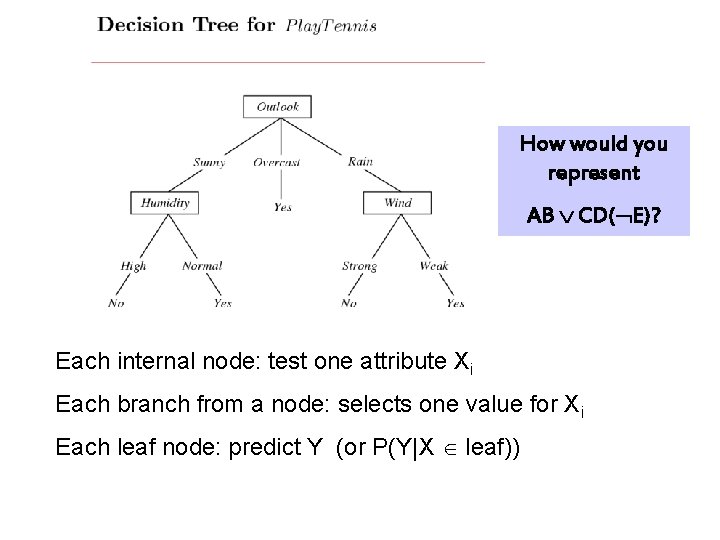
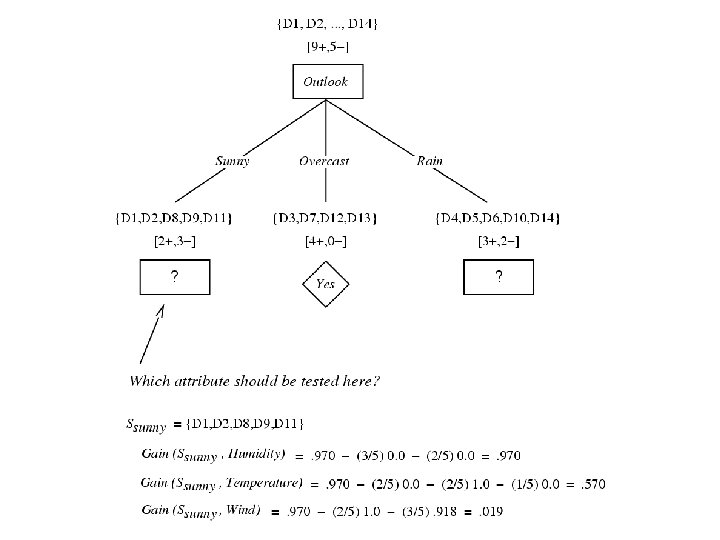
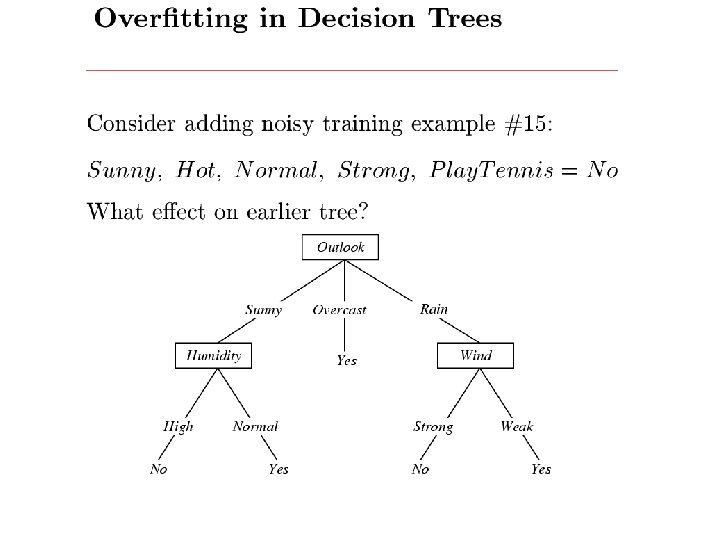
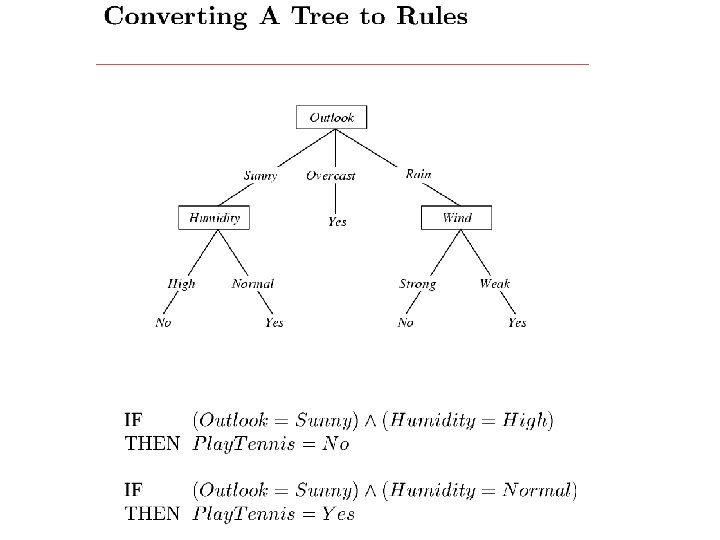
How would you represent AB CD( E)? Each internal node: test one attribute Xi Each branch from a node: selects one value for Xi Each leaf node: predict Y (or P(Y|X leaf))

![ID 3 C 4 5 node Root [ID 3, C 4. 5, …] node = Root](https://slidetodoc.com/presentation_image_h/794c28b6def3f22e99a24390e207fef8/image-15.jpg)
[ID 3, C 4. 5, …] node = Root

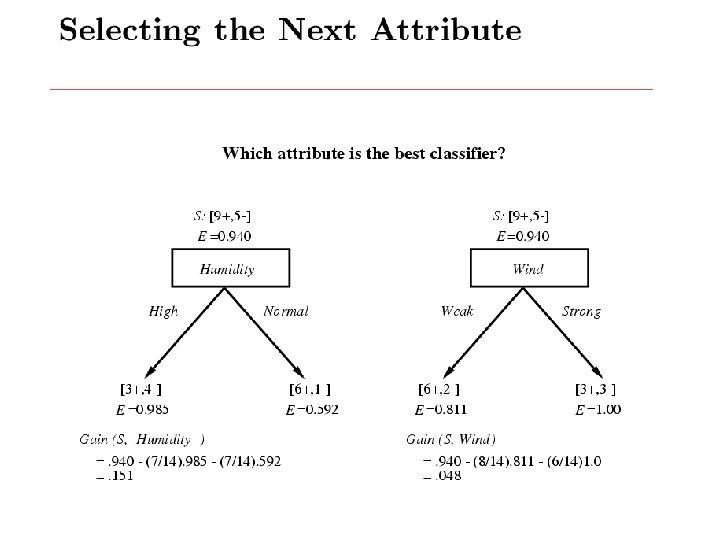
Entropy H(X) of a random variable X H(X) is the expected number of bits needed to encode a randomly drawn value of X (under most efficient code) Why? Information theory: • Most efficient code assigns -log 2 P(X=i) bits to encode the message X=i • So, expected number of bits to code one random X is: # of possible values for X

Entropy H(X) of a random variable X Specific conditional entropy H(X|Y=v) of X given Y=v : Conditional entropy H(X|Y) of X given Y : Mututal information (aka information gain) of X and Y :

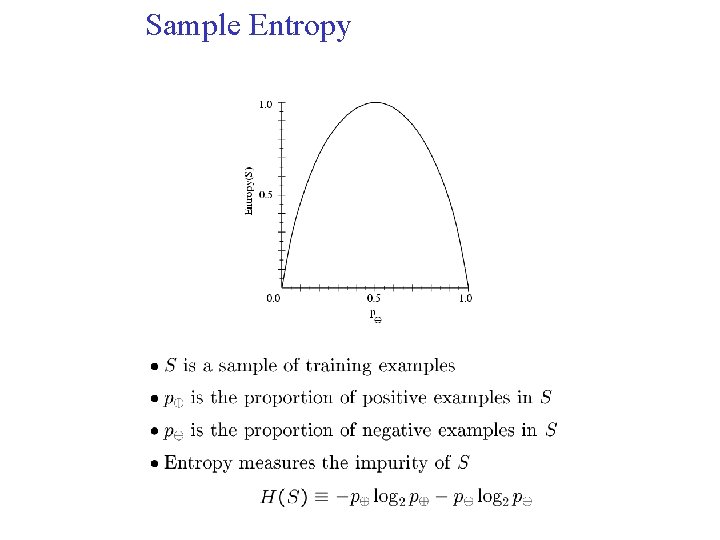
Sample Entropy

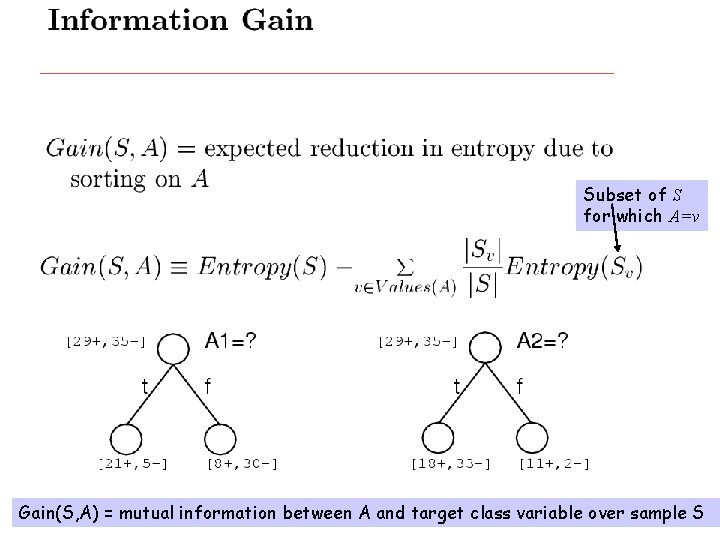
Subset of S for which A=v Gain(S, A) = mutual information between A and target class variable over sample S




Decision Tree Learning Applet • http: //www. cs. ualberta. ca/%7 Eaixplore/l earning/Decision. Trees/Applet/Decision Tree. Applet. html

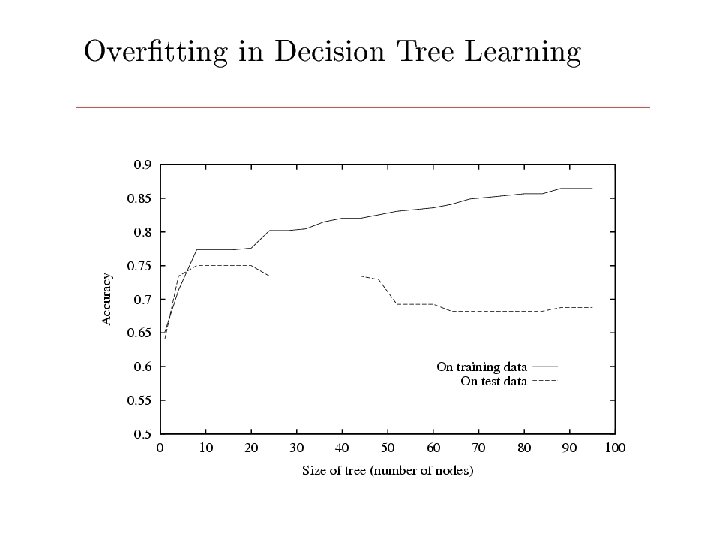
Which Tree Should We Output? • ID 3 performs heuristic search through space of decision trees • It stops at smallest acceptable tree. Why? Occam’s razor: prefer the simplest hypothesis that fits the data

Why Prefer Short Hypotheses? (Occam’s Razor) Argument in favor: • Fewer short hypotheses than long ones a short hypothesis that fits the data is less likely to be a statistical coincidence highly probable that a sufficiently complex hypothesis will fit the data Argument opposed: • Also fewer hypotheses with prime number of nodes and attributes beginning with “Z” • What’s so special about “short” hypotheses?





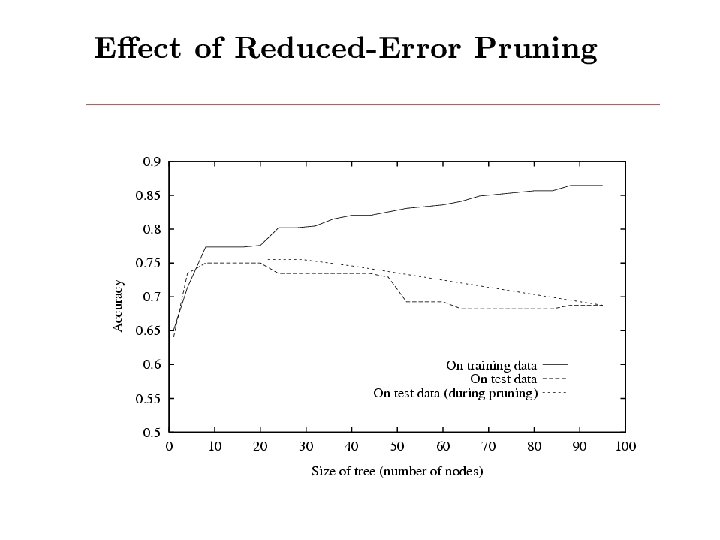
Split data into training and validation set Create tree that classifies training set correctly







What you should know: • Well posed function approximation problems: – Instance space, X – Sample of labeled training data { <xi, yi>} – Hypothesis space, H = { f: X Y } • Learning is a search/optimization problem over H – Various objective functions • minimize training error (0 -1 loss) • among hypotheses that minimize training error, select shortest • Decision tree learning – Greedy top-down learning of decision trees (ID 3, C 4. 5, . . . ) – Overfitting and tree/rule post-pruning – Extensions…

Questions to think about (1) • Why use Information Gain to select attributes in decision trees? What other criteria seem reasonable, and what are the tradeoffs in making this choice?

Questions to think about (2) • ID 3 and C 4. 5 are heuristic algorithms that search through the space of decision trees. Why not just do an exhaustive search?

Questions to think about (3) • Consider target function f: <x 1, x 2> y, where x 1 and x 2 are real-valued, y is boolean. What is the set of decision surfaces describable with decision trees that use each attribute at most once?
 Tom mitchell machine learning solutions chapter 3
Tom mitchell machine learning solutions chapter 3 Tom mitchell machine learning definition
Tom mitchell machine learning definition Machine learning t mitchell
Machine learning t mitchell Objectives of decision making
Objectives of decision making Investment decision financing decision dividend decision
Investment decision financing decision dividend decision Decision tree machine learning andrew ng
Decision tree machine learning andrew ng Pre reading while reading and post reading activities
Pre reading while reading and post reading activities Underfitting and overfitting in data mining
Underfitting and overfitting in data mining Naive bayes dataset
Naive bayes dataset Churn avoidance
Churn avoidance Overfitting
Overfitting Overfitting
Overfitting Overfitting in data mining
Overfitting in data mining Overfitting in data mining
Overfitting in data mining Nn overfitting
Nn overfitting Smote overfitting
Smote overfitting Supply chain network design decisions
Supply chain network design decisions Decision making trees
Decision making trees Data and process modeling
Data and process modeling Concept learning task in machine learning
Concept learning task in machine learning Analytical learning in machine learning
Analytical learning in machine learning Pac learning model in machine learning
Pac learning model in machine learning Inductive and analytical learning in machine learning
Inductive and analytical learning in machine learning Deductive learning vs inductive learning
Deductive learning vs inductive learning Instance based learning in machine learning
Instance based learning in machine learning Inductive learning machine learning
Inductive learning machine learning First order rule learning in machine learning
First order rule learning in machine learning Eager learning algorithm example
Eager learning algorithm example Deep learning vs machine learning
Deep learning vs machine learning Cuadro comparativo entre e-learning b-learning y m-learning
Cuadro comparativo entre e-learning b-learning y m-learning Cladogram vs phylogram
Cladogram vs phylogram Decision table and decision tree examples
Decision table and decision tree examples Turbine crossflow
Turbine crossflow Nickole mitchell
Nickole mitchell Theology and falsification
Theology and falsification Social crm mitchell1
Social crm mitchell1 Clasificacion de wong mitchell
Clasificacion de wong mitchell Retinopata
Retinopata Classification de mitchell ostéonécrose
Classification de mitchell ostéonécrose Mitchell daysh
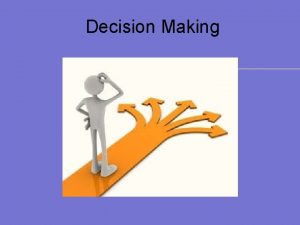
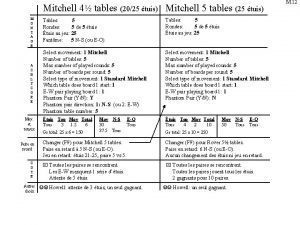
Mitchell daysh 4 table mitchell movement
4 table mitchell movement