Recursive Random Fields Daniel Lowd University of Washington

Recursive Random Fields Daniel Lowd University of Washington (Joint work with Pedro Domingos)

One-Slide Summary Question: How to represent uncertainty in relational domains? l State-of-the-Art: Markov logic [Richardson & Domingos, 2004] l ¡ l l Markov logic network (MLN) = First-order KB with weights: Problem: Only top-level conjunction and universal quantifiers are probabilistic Solution: Recursive random fields (RRFs) ¡ ¡ ¡ RRF = MLN whose features are MLNs Inference: Gibbs sampling, iterated conditional modes Learning: Back-propagation

Overview Example: Friends and Smokers l Recursive random fields l ¡ ¡ ¡ Representation Inference Learning Experiments: Databases with probabilistic integrity constraints l Future work and conclusion l

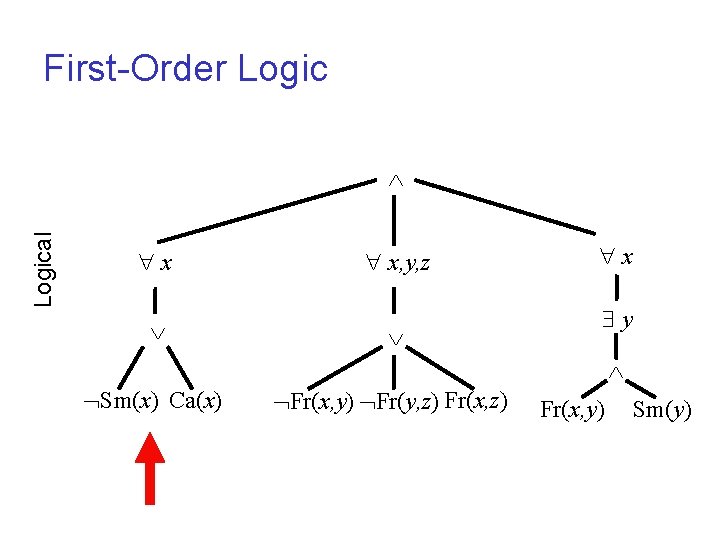
Example: Friends and Smokers [Richardson and Domingos, 2004] Predicates: Smokes(x); Cancer(x); Friends(x, y) We wish to represent beliefs such as: l Smoking causes cancer l Friends of friends are friends (transitivity) l Everyone has a friend who smokes

First-Order Logical x x, y, z x y Sm(x) Ca(x) Fr(x, y) Fr(y, z) Fr(x, y) Sm(y)

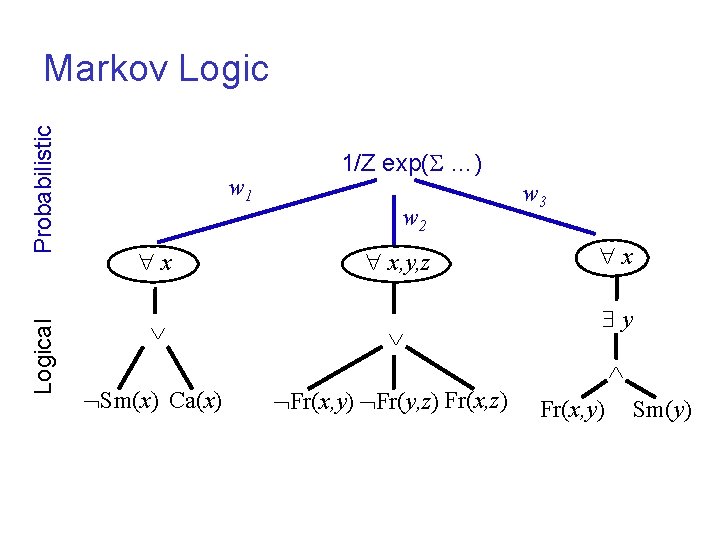
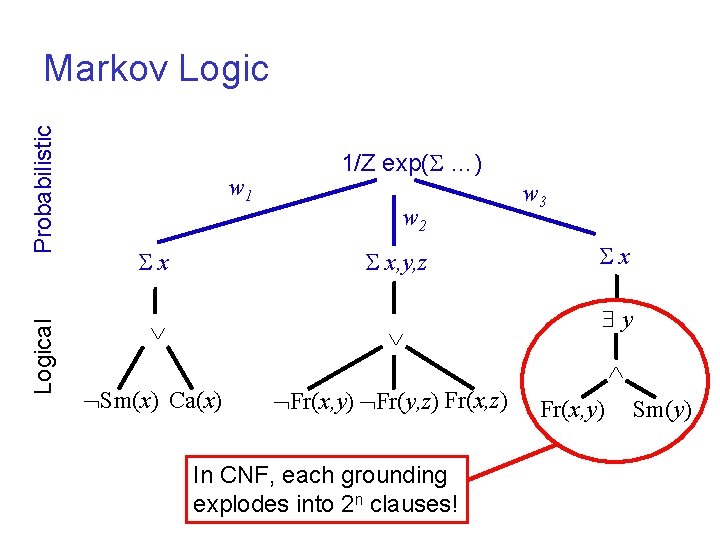
Logical Probabilistic Markov Logic w 1 x 1/Z exp( …) w 2 x, y, z w 3 x y Sm(x) Ca(x) Fr(x, y) Fr(y, z) Fr(x, y) Sm(y)

Logical Probabilistic Markov Logic w 1 x 1/Z exp( …) w 2 x, y, z w 3 x y Sm(x) Ca(x) Fr(x, y) Fr(y, z) Fr(x, y) Sm(y)

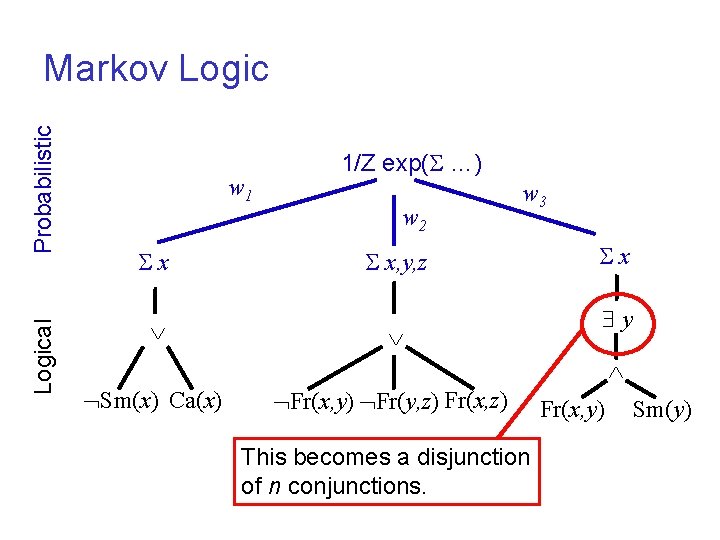
Logical Probabilistic Markov Logic w 1 x 1/Z exp( …) w 2 w 3 x, y, z x y Sm(x) Ca(x) Fr(x, y) Fr(y, z) Fr(x, z) This becomes a disjunction of n conjunctions. Fr(x, y) Sm(y)

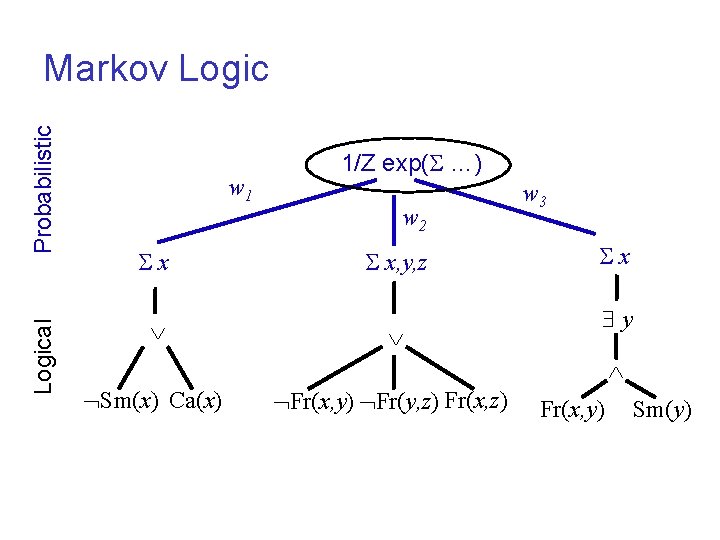
Logical Probabilistic Markov Logic w 1 x 1/Z exp( …) w 2 x, y, z w 3 x y Sm(x) Ca(x) Fr(x, y) Fr(y, z) Fr(x, z) In CNF, each grounding explodes into 2 n clauses! Fr(x, y) Sm(y)

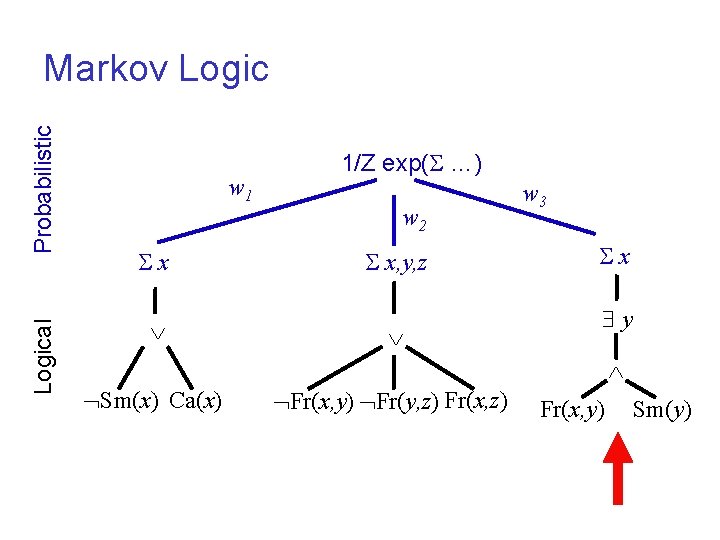
Logical Probabilistic Markov Logic w 1 x 1/Z exp( …) w 2 x, y, z w 3 x y Sm(x) Ca(x) Fr(x, y) Fr(y, z) Fr(x, y) Sm(y)

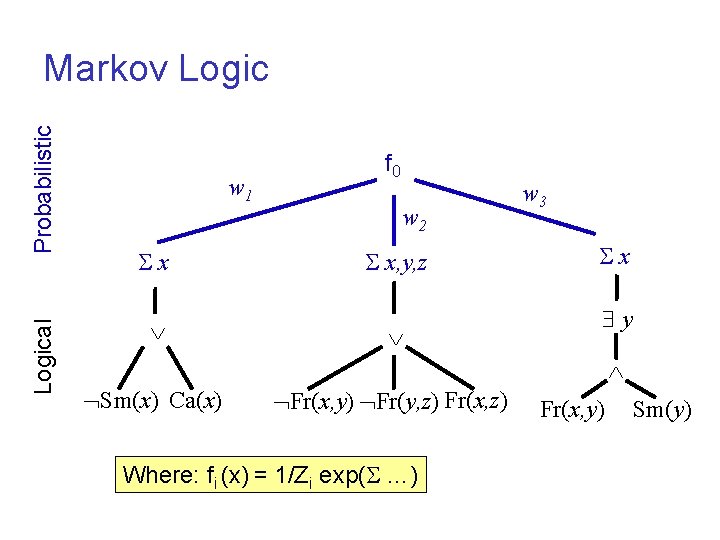
Logical Probabilistic Markov Logic w 1 x f 0 w 2 x, y, z w 3 x y Sm(x) Ca(x) Fr(x, y) Fr(y, z) Fr(x, z) Where: fi (x) = 1/Zi exp( …) Fr(x, y) Sm(y)

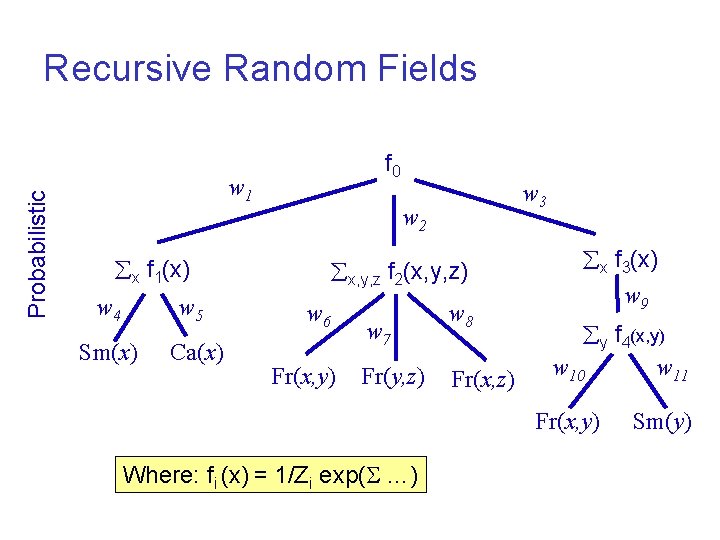
Probabilistic Recursive Random Fields f 0 w 1 w 2 x f 1(x) w 4 w 5 Sm(x) Ca(x) w 3 x, y, z f 2(x, y, z) w 6 Fr(x, y) w 7 Fr(y, z) w 8 Fr(x, z) x f 3(x) w 9 y f 4(x, y) w 10 w 11 Fr(x, y) Where: fi (x) = 1/Zi exp( …) Sm(y)

The RRF Model RRF features are parameterized and are grounded using objects in the domain. ¡ Leaves = Predicates: ¡ Recursive features are built up from other RRF features:

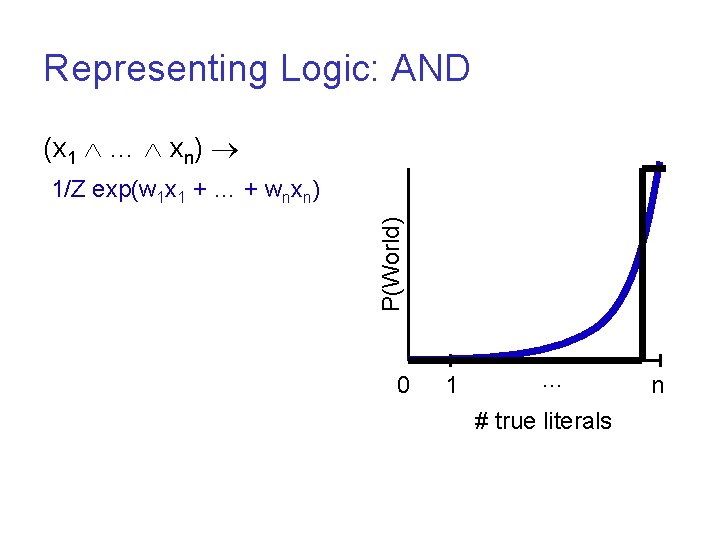
Representing Logic: AND (x 1 … xn) P(World) 1/Z exp(w 1 x 1 + … + wnxn) 0 1 … # true literals n

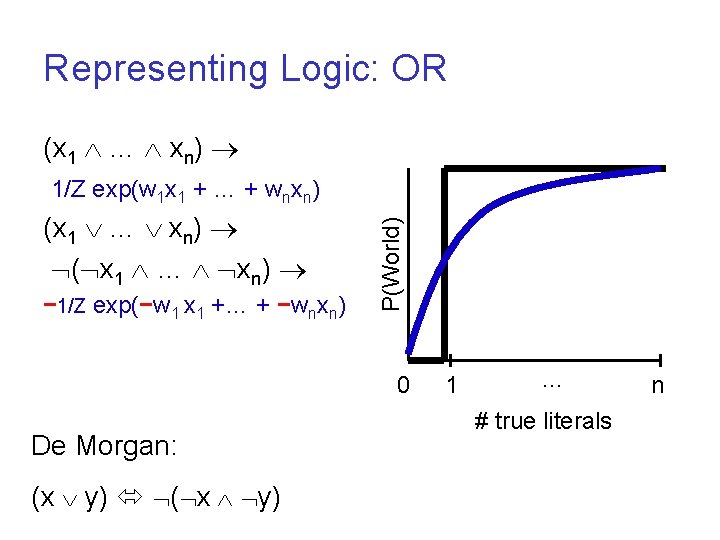
Representing Logic: OR (x 1 … xn) ( x 1 … xn) − 1/Z exp(−w 1 x 1 +… + −wnxn) P(World) 1/Z exp(w 1 x 1 + … + wnxn) 0 De Morgan: (x y) ( x y) 1 … # true literals n

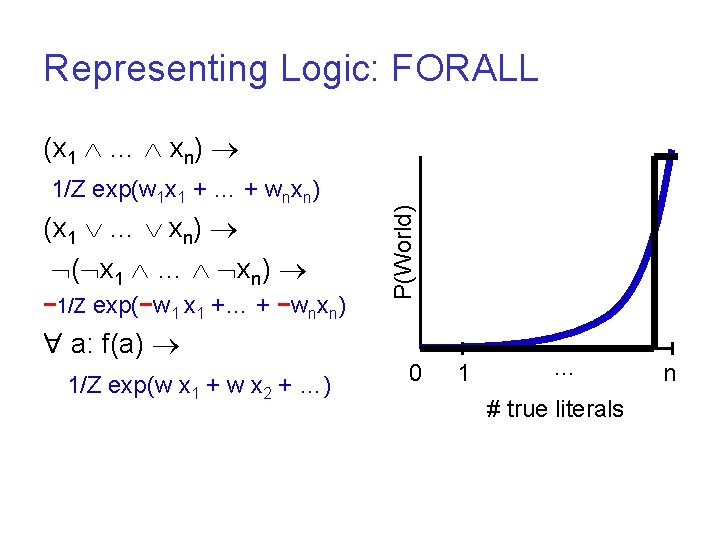
Representing Logic: FORALL 1/Z exp(w 1 x 1 + … + wnxn) (x 1 … xn) ( x 1 … xn) − 1/Z exp(−w 1 x 1 +… + −wnxn) P(World) (x 1 … xn) a: f(a) 1/Z exp(w x 1 + w x 2 + …) 0 1 … # true literals n

Representing Logic: EXIST 1/Z exp(w 1 x 1 + … + wnxn) (x 1 … xn) ( x 1 … xn) − 1/Z exp(−w 1 x 1 +… + −wnxn) P(World) (x 1 … xn) a: f(a) 1/Z exp(w x 1 + w x 2 + …) a: f(a) ( a: f(a)) − 1/Z exp(−w x 1 + −w x 2 + …) 0 1 … # true literals n

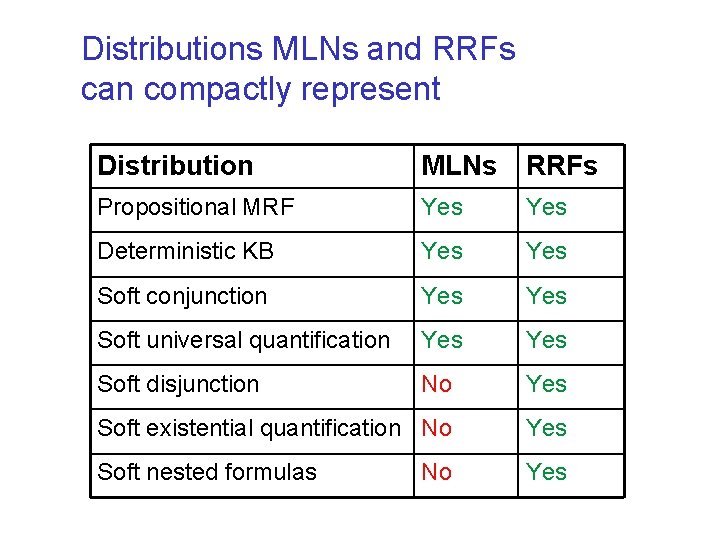
Distributions MLNs and RRFs can compactly represent Distribution MLNs RRFs Propositional MRF Yes Deterministic KB Yes Soft conjunction Yes Soft universal quantification Yes Soft disjunction No Yes Soft existential quantification No Yes Soft nested formulas Yes No

Inference and Learning l Inference ¡ MAP: Iterated conditional modes (ICM) ¡ Conditional probabilities: Gibbs sampling l Learning ¡ Back-propagation ¡ Pseudo-likelihood ¡ RRF weight learning is more powerful than MLN structure learning (cf. KBANN) ¡ More flexible theory revision

Experiments: Databases with Probabilistic Integrity Constraints l Integrity ¡ ¡ constraints: First-order logic Inclusion: “If x is in table R, it must also be in table S” Functional dependency: “In table R, each x determines a unique y” l Need to make them probabilistic l Perfect application of MLNs/RRFs

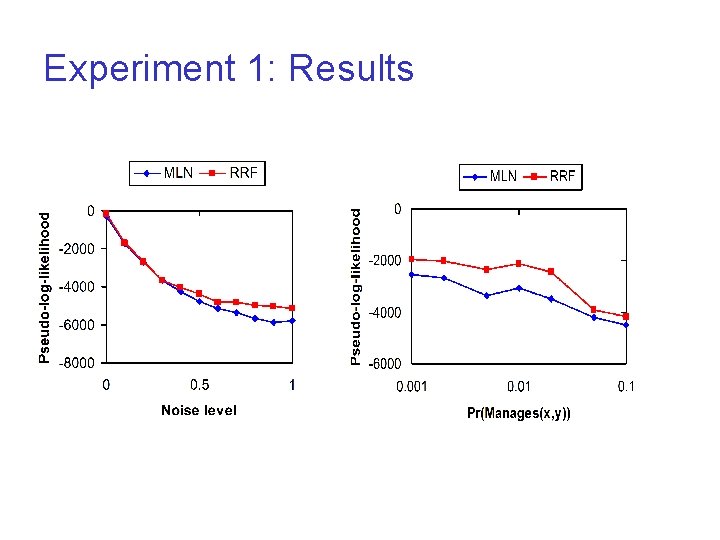
Experiment 1: Inclusion Constraints Task: Clean a corrupt database l Relations l ¡ ¡ ¡ l Project. Lead(x, y) – x is in charge of project y Manager. Of(x, z) – x manages employee z Corrupt versions: Project. Lead’(x, y); Manager. Of’(x, z) Constraints ¡ ¡ Every project leader manages at least one employee. i. e. , x. ( y. Project. Lead(x, y)) ( z. Manages(x, z)) Corrupt database is related to original database i. e. , Project. Lead(x, y) Project. Lead’(x, y)

Experiment 1: Inclusion Constraints l Data 100 people, 100 projects ¡ 25% are managers of ~10 projects each, and manage ~5 employees per project ¡ Added extra Manager. Of(x, y) relations ¡ Predicate truth values flipped with probability p ¡ l Models ¡ ¡ Converted FOL to MLN and RRF Maximized pseudo-likelihood

Experiment 1: Results

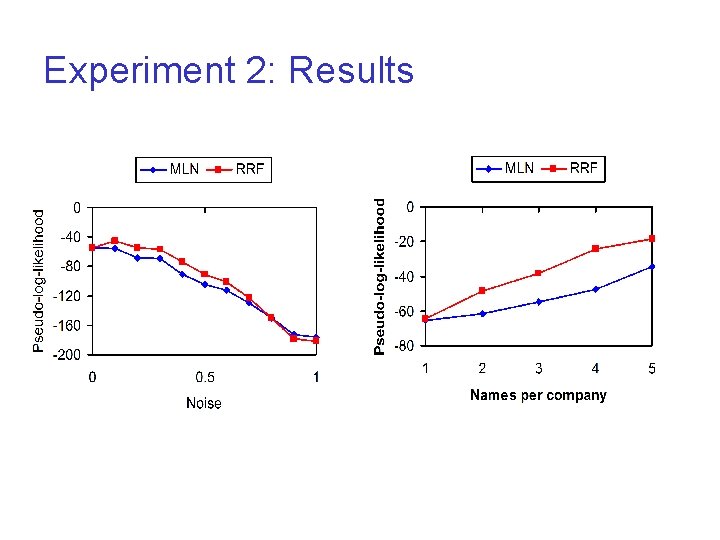
Experiment 2: Functional Dependencies Task: Determine which names are pseudonyms l Relation: l ¡ l Supplier(Tax. ID, Company. Name, Part. Type) – Describes a company that supplies parts Constraint ¡ Company names with same Tax. ID are equivalent i. e. , x, y 1, y 2. ( z 1, z 2. Supplier(x, y 1, z 1) Supplier(x, y 2, z 2) ) y 1 = y 2

Experiment 2: Functional Dependencies l Data ¡ ¡ l 30 tax IDs, 30 company names, 30 part types Each company supplies 25% of all part types Each company has k names Company names are changed with probability p Models ¡ ¡ Converted FOL to MLN and RRF Maximized pseudo-likelihood

Experiment 2: Results

Future Work l Scaling up ¡ ¡ l Experiments with real-world databases ¡ ¡ l Pruning, caching Alternatives to Gibbs, ICM, gradient descent Probabilistic integrity constraints Information extraction, etc. Extract information a la TREPAN (Craven and Shavlik, 1995)

Conclusion Recursive random fields: – Less intuitive than Markov logic – More computationally costly + Compactly represent many distributions MLNs cannot + Make conjunctions, existentials, and nested formulas probabilistic + Offer new methods for structure learning and theory revision Questions: lowd@cs. washington. edu