ADM 4007 Finanas Corporativas Decises em Condies de

ADM 4007 Finanças Corporativas Decisões em Condições de Risco Os Modelos de Markowitz e Sharpe, o CAPM Parte 2 Baseado em SECURATO, J. R. Decisões financeiras em condições de risco. São Paulo: Atlas, 1996.

Fronteira Eficiente de Ativos com Risco Considere uma carteira de investimentos composta dos ativos A 1, A 2 e A 3, nas proporções w 1, w 2 e w 3, respectivamente. São conhecidos os retornos médios Im 1, Im 2 e Im 3, bem como os desvios IS 1, IS 2 e IS 3, respectivamente. As covariâncias dos retornos dos ativos são dadas por: cov(I 1, I 2 ), cov(I 1, I 3) e cov(IS 2, IS 3).

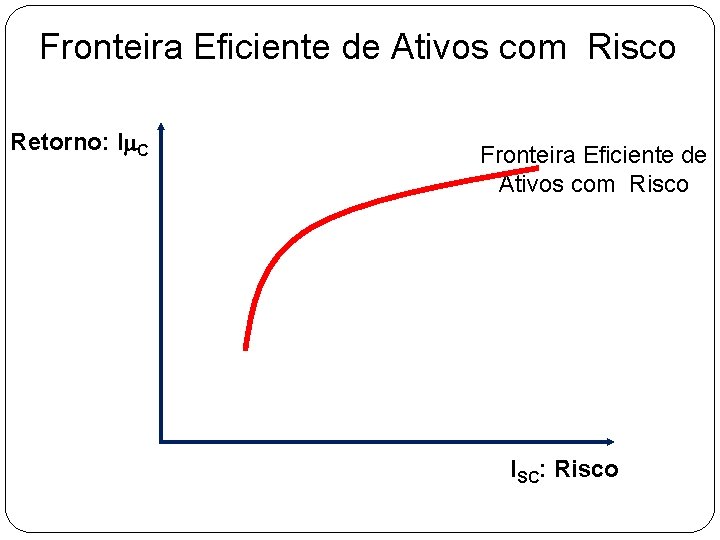
Fronteira Eficiente de Ativos com Risco Retorno: Im. C Fronteira Eficiente de Ativos com Risco ISC: Risco

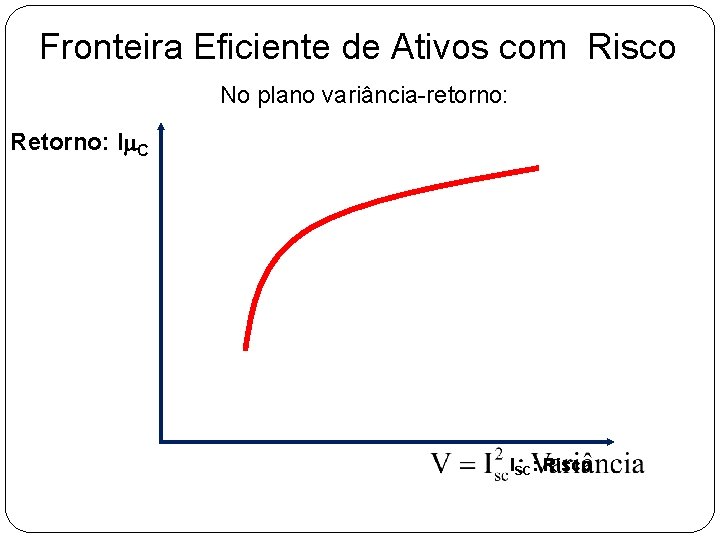
Fronteira Eficiente de Ativos com Risco No plano variância-retorno: Retorno: Im. C ISC: Risco

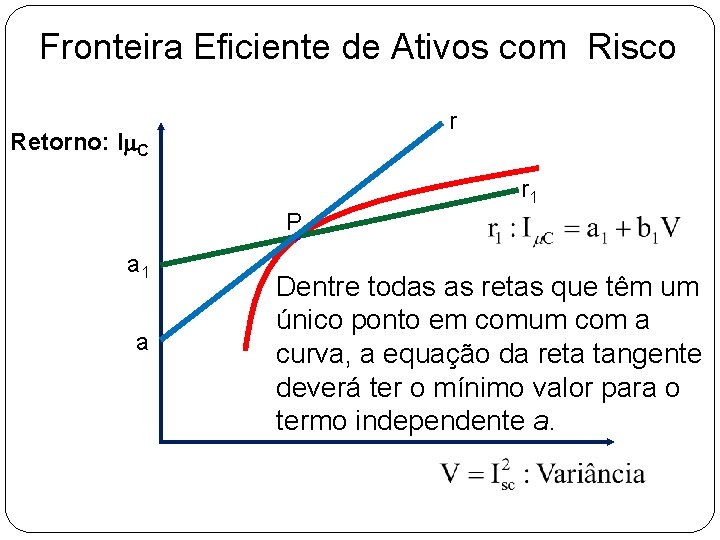
Fronteira Eficiente de Ativos com Risco r Retorno: Im. C r 1 P a 1 a Dentre todas as retas que têm um único ponto em comum com a curva, a equação da reta tangente deverá ter o mínimo valor para o termo independente a.

Diversificação do Risco de uma Carteira Equações das retas que passam por P: Condição para que seja tangente à curva: Ponto P: Em termos de variância retorno Em termos de composição da carteira

Diversificação do Risco de uma Carteira Assim, o ponto P deve satisfazer às seguintes condições: e Em que e

Diversificação do Risco de uma Carteira Obtidos os pontos Pode-se obter os pontos que serão pontos da fronteira eficiente de investimentos dos ativos com risco, ambos definidos pela mesma composição das carteiras. Próximo passo: obter a composição da carteira que dá os pontos tipo P.

Diversificação do Risco de uma Carteira Obter tais que: com Ou seja Função a ser minimizada: submetida à restrição Pelo método do multiplicador de Lagrange, tem-se a função objetivo dada por:

Diversificação do Risco de uma Carteira Deve-se resolver o sistema:

Diversificação do Risco de uma Carteira Substituindo os valores de tem-se: (PAG. 195)

Diversificação do Risco de uma Carteira Reescrevendo o sistema:

Diversificação do Risco de uma Carteira Que escrito na forma matricial: Que pode ser indicado por: M. W = U Resolvendo obtém-se: W =M-1 U O que possibilita obter (w 1, w 2, w 3) em função do coeficiente b.

Diversificação do Risco de uma Carteira Que escrito na forma matricial: Deve-se verificar se a condição 0 ≤ w 1, w 2, w 3 ≤ 1) está satisfeita. (o método não capta se ocorre ou não esta condição). Que pode ser indicado por: M. W = U Resolvendo obtém-se: W =M-1 U O que possibilita obter (w 1, w 2, w 3) em função do coeficiente b.

Modelo de Markowitz – caso geral Que pode ser indicado por: M. W = U Resolvendo obtém-se: W =M-1 U O que possibilita obter (w 1, w 2, . . . , wn) em função do coeficiente b.

Modelo de Markowitz – caso geral Exemplo: Im 1 = 0, 15; IS 1 = 0, 05 cov(I 1, I 2) = 0, 00245 Im 2 = 0, 25; IS 2 = 0, 07 cov(I 1, I 3) = 0, 00100 Im 3 = 0, 35; IS 3 = 0, 10 cov(I 2, I 3) = 0, 00350

Modelo de Markowitz – caso geral Resolvendo:

Modelo de Markowitz – caso geral Questões: Verifique se w 1 + w 2 + w 3 = 1 Qual é a equação do retorno médio da carteira? Qual é a equação do risco da carteira? Qual o retorno no ponto de mínimo risco? (dica: pense em qual deve ser o valor de b no vértice da parábola) 5) Qual é o valor do desvio no ponto de risco mínimo? 6) Qual é a composição da carteira no ponto de risco mínimo? 7) Para quais valores de b são obtidos os pontos da fronteira eficiente? 1) 2) 3) 4)

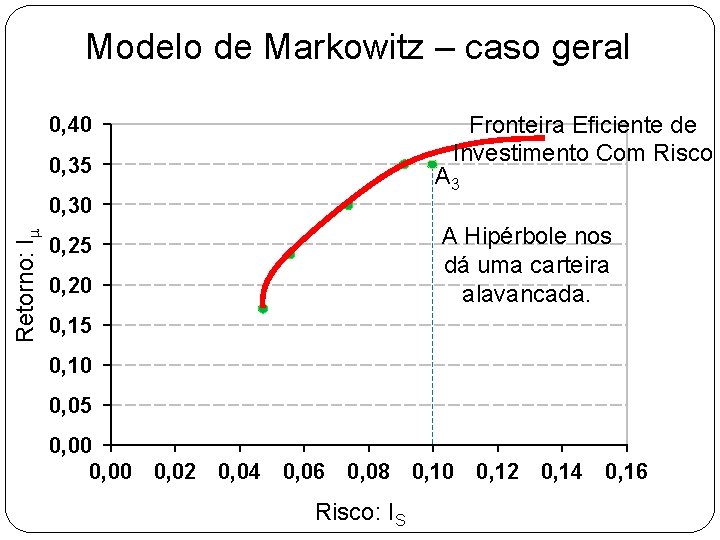
Modelo de Markowitz – caso geral Fronteira Eficiente de Investimento Com Risco 0, 40 0, 35 A 3 Retorno: Im 0, 30 A Hipérbole nos dá uma carteira alavancada. 0, 25 0, 20 0, 15 0, 10 0, 05 0, 00 0, 02 0, 04 0, 06 0, 08 0, 10 0, 12 0, 14 0, 16 Risco: IS

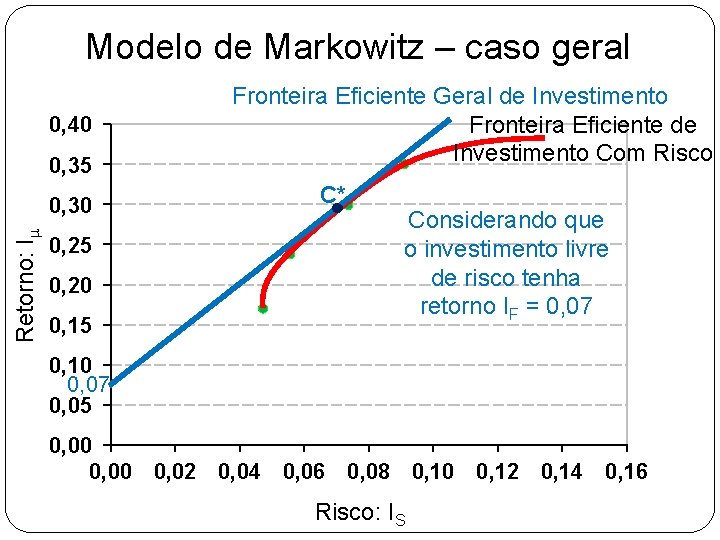
Modelo de Markowitz – caso geral 0, 40 0, 35 Retorno: Im 0, 30 0, 25 0, 20 0, 15 Fronteira Eficiente Geral de Investimento Fronteira Eficiente de Investimento Com Risco C* Considerando que o investimento livre de risco tenha retorno IF = 0, 07 0, 10 0, 07 0, 05 0, 00 0, 02 0, 04 0, 06 0, 08 0, 10 0, 12 0, 14 0, 16 Risco: IS

Carteira de Máxima Razão Recompensa -Variabilidade Conforme a definição de Sharpe, a razão recompensa-variabilidade de um ativo A, indicada por RVA, é dada por: Estendendo o conceito para uma carteira C, temse:

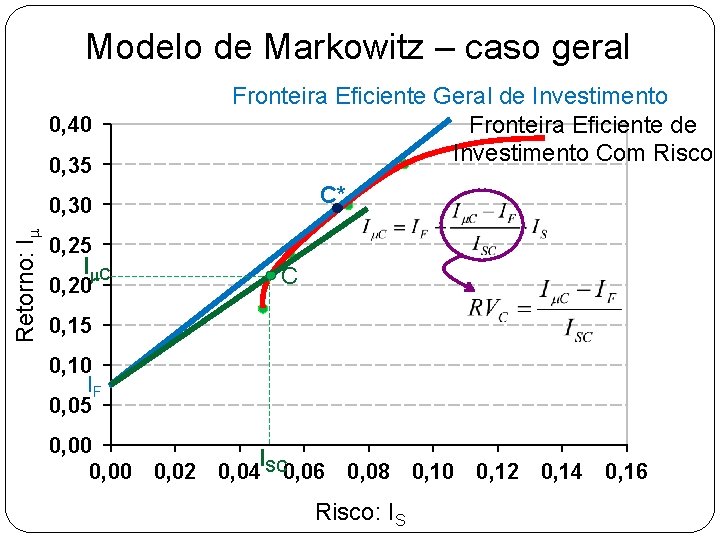
Modelo de Markowitz – caso geral 0, 40 0, 35 Fronteira Eficiente Geral de Investimento Fronteira Eficiente de Investimento Com Risco C* Retorno: Im 0, 30 0, 25 Im. C 0, 20 C 0, 15 0, 10 IF 0, 05 0, 00 I 0, 00 0, 02 0, 04 SC 0, 06 0, 08 0, 10 0, 12 0, 14 0, 16 Risco: IS

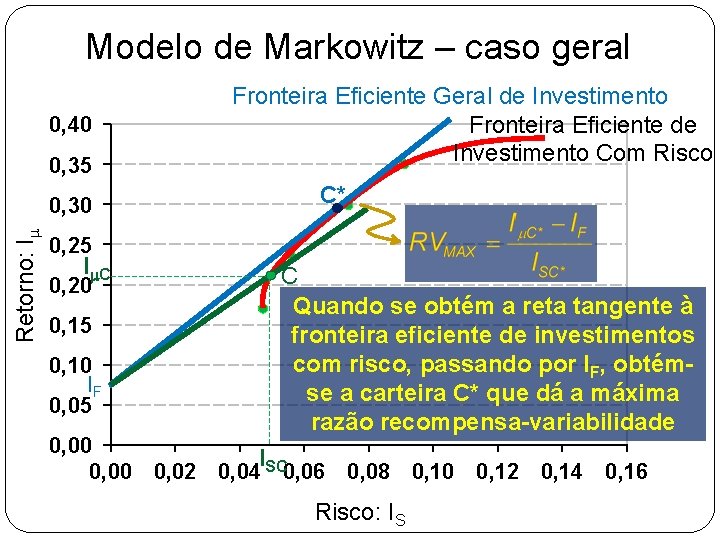
Modelo de Markowitz – caso geral 0, 40 0, 35 Retorno: Im 0, 30 Fronteira Eficiente Geral de Investimento Fronteira Eficiente de Investimento Com Risco C* 0, 25 Im. C 0, 20 0, 15 0, 10 IF 0, 05 C Quando se obtém a reta tangente à fronteira eficiente de investimentos com risco, passando por IF, obtémse a carteira C* que dá a máxima razão recompensa-variabilidade 0, 00 I 0, 00 0, 02 0, 04 SC 0, 06 0, 08 0, 10 0, 12 0, 14 0, 16 Risco: IS

Carteira de Risco Mínimo para um Retorno Fixado Ver item 6. 4 (p. 207) de SECURATO, J. R. Decisões financeiras em condições de risco. São Paulo: Atlas, 1996.

Modelo de SHARPE Dificuldade no modelo de Markovitz: - Estabelecer as covariâncias entre os retornos dos ativos que iriam compor as várias carteiras que seriam analisadas (grande número de cálculos). Ideia inicial: substituir as covariâncias pelos coeficientes de correlação linear, visto que

Modelo de SHARPE Idéia inicial: substituir as covariâncias pelos coeficientes de correlação linear, visto que: • Até aqui, poucas vantagens, apenas trocou o cálculo das covariâncias pelo cálculo dos coeficientes de correlação. . . • Seria possível calcular o coeficiente de correlação linear dos retornos dos ativos A 1, A 2, . . . , An, em relação a um único ativo, que atuaria como uma espécie de padrão para as comparações?

Modelo de SHARPE • Seria possível calcular o coeficiente de correlação linear dos retornos dos ativos A 1, A 2, . . . , An, em relação a um único ativo, que atuaria como uma espécie de padrão para as comparações? • Se tivéssemos este ativo padrão poderíamos comparar o retorno de cada ativo com o retorno desse ativo padrão e examinar o grau de correlação linear. IBOVESPA, por exemplo.

Modelo de SHARPE Ver itens 6. 5 e 6. 6 de SECURATO, J. R. Decisões financeiras em condições de risco. São Paulo: Atlas, 1996.

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros 1. Os investidores preocupam-se apenas com o valor esperado e com a variância (ou o desvio padrão) da taxa de retorno. 2. Os investidores têm preferências por retorno maior e risco menor. 3. Os investidores desejam ter carteiras eficientes: aquelas que dão o máximo retorno esperado, dado o risco, ou mínimo risco, dado o retorno esperado. 4. Os investidores estão de acordo quanto à distribuição de probabilidades das taxas de retorno dos ativos, o que assegura a existência de um único conjunto de carteiras eficientes. Aceitação da relação risco-retorno • O desenvolvimento do CAPM baseia-se em algumas hipóteses:

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros • O desenvolvimento do CAPM baseia-se em algumas hipóteses: 5. Os ativos são perfeitamente divisíveis. 6. Há um ativo sem risco, e os investidores podem comprá-lo e vendê-lo em qualquer quantidade. 7. Não há custo de transação ou impostos, ou, alternativamente, eles são idênticos para todos os indivíduos. As hipóteses implicam em condições de mercado perfeito.

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Seja M a carteira de mercado (todos ativos do mercado), em que seu retorno RM apresenta média Rm. M e risco/desvio RSM. Considere um ativo de risco A com retorno IA, de média Rm. A e risco/desvio RSA. F é um ativo livre de risco com retorno IF. Deseja-se montar uma carteira C composta pelo ativo A e por M.

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros e Pode-se examinar o que ocorre com o risco e o retorno à medida que variamos a proporção w do ativo A na carteira, calculando:

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Coeficiente angular das retas tangentes à hipérbole:

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Se w 0, a composição de M é alterada. Assim, a condição de equilíbrio de mercado ocorre para w = 0, ou seja, quando não há procura do ativo A em proporções maiores do que sua participação na carteira de mercado M.

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Para w = 0:

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Para as carteiras C, formadas pelos ativos A e M (w 0), a razão recompensa-variabilidade é: Condição de máxima razão recompensa-variabilidade:

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Condição de máxima razão recompensa-variabilidade:

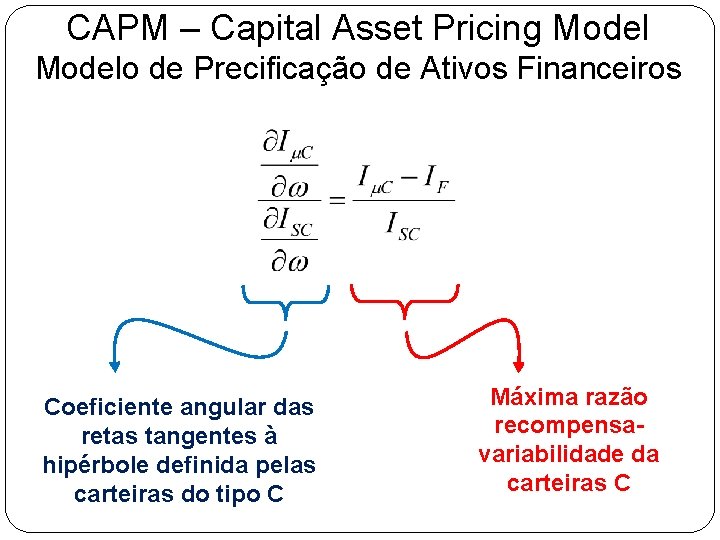
CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Coeficiente angular das retas tangentes à hipérbole definida pelas carteiras do tipo C Máxima razão recompensavariabilidade da carteiras C

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Em condição de equilíbrio, w = 0, ou seja, C = M:

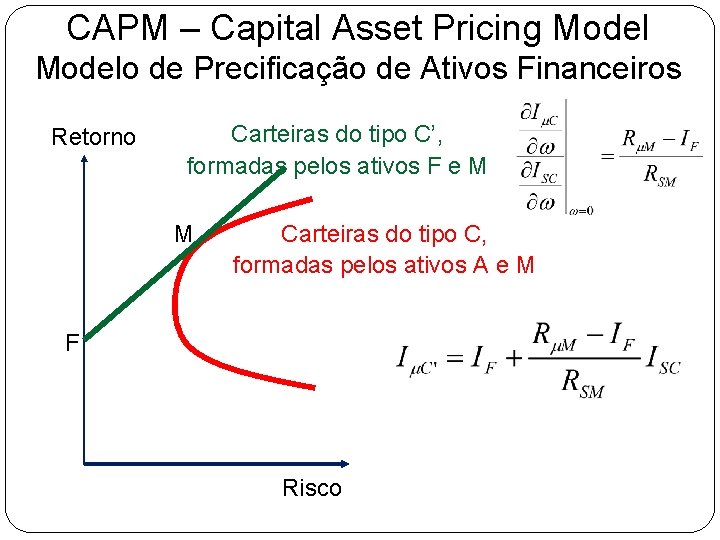
CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Retorno Carteiras do tipo C’, formadas pelos ativos F e M M Carteiras do tipo C, formadas pelos ativos A e M F Risco

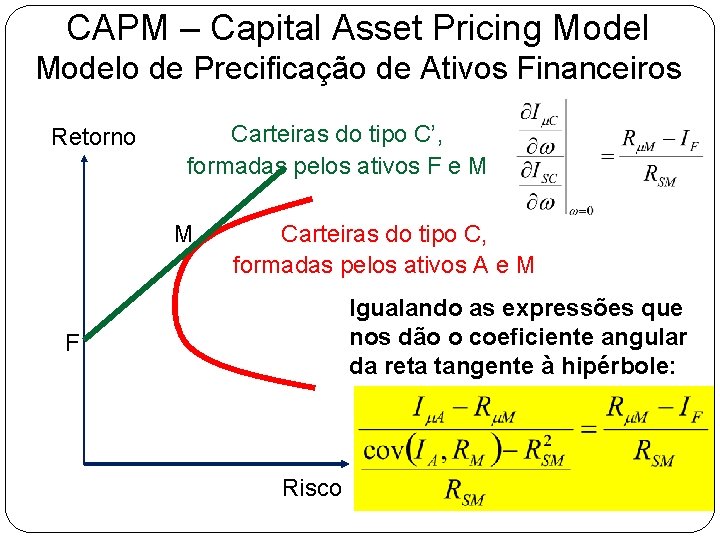
CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Retorno Carteiras do tipo C’, formadas pelos ativos F e M M Carteiras do tipo C, formadas pelos ativos A e M Igualando as expressões que nos dão o coeficiente angular da reta tangente à hipérbole: F Risco

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros

CAPM – Capital Asset Pricing Modelo de Precificação de Ativos Financeiros Esta expressão, obtida por Sharpe, é a equação fundamental do CAPM, caracterizando que o preço de um ativo A, ou seja, seu retorno médio Im. A, é formado por duas parcelas:

Bibliografia GITMAN, Lawrence J. Princípios de administração financeira. São Paulo: Harbra, 1984, p. 131, 144. JORION, P. (2003). Value at risk: a nova fonte de referência para a gestão do risco. Segunda edição. Bolsa de Mercadorias & Futuros. São Paulo. LINSMEIER, T. & PEARSON, N. (2000). Value at Risk. Financial Analyst Journal. pp: 47, 67. SADEGHI, M. & SHAVVALPOUR, S. (2006). Energy risk management and value at risk modeling. Energy Policy (34). pp: 3367 -3373.

Bibliografia SECURATO, J, R. Decisões Financeiras em condições de risco. São Paulo: Saint Paul Editora, 2007. SOLOMON, Ezra, PRINGLE, John. Introdução à administração financeira. São Paulo: Atlas, 1981.