A Framework for Mathematical Knowledge for Teaching at

A Framework for Mathematical Knowledge for Teaching at the Secondary Level Conference on Knowledge of Mathematics for Teaching at the Secondary Level Pat Wilson pswilson@uga. edu Kathy Heid mkh 2@psu. edu Tucson, AZ --- March 2011� Mid Atlantic Center for Mathematics Teaching and Learning Center for Proficiency in Teaching Mathematics

Situations Project • Classroom-based situations • A framework for mathematical knowledge at the secondary level

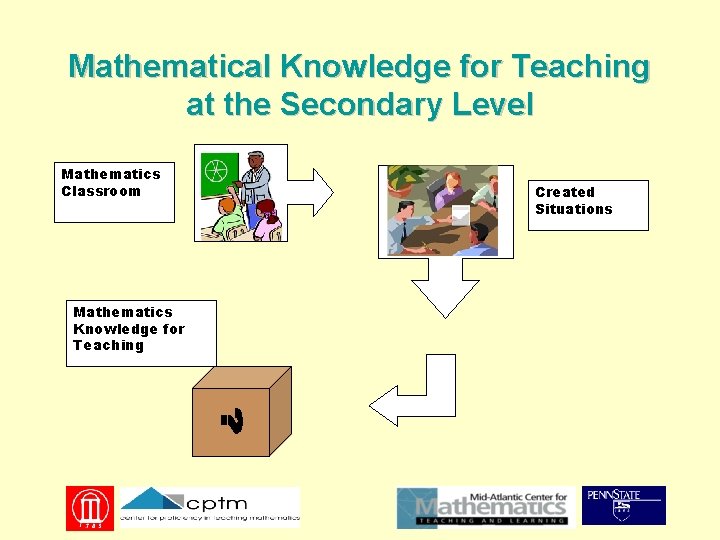
Mathematical Knowledge for Teaching at the Secondary Level Mathematics Classroom Mathematics Knowledge for Teaching Created Situations

Mathematical Knowledge for Teaching Mathematics at the Secondary Level What is MKTS? • MKTS is specialized mathematical knowledge • Knowing mathematics • Being able to and having a tendency to use the mathematics in appropriate circumstances • MKTS is not pedagogical knowledge. How is MKTS different from MKT elementary?

Examples of Situations • Prompt • Mathematical Foci

Circumscribing Polygons Prompt In a geometry class, after a discussion about circumscribing circles about triangles, a student asked, “Can you circumscribe a circle about any polygon? ” A few mathematical foci • Every triangle is cyclic. This fact is core to establishing a condition for other polygons to be cyclic. • A convex quadrilateral in a plane is cyclic if and only if its opposite angles are supplementary. • Every planar regular polygon is cyclic. However, not every cyclic polygon is regular.

Summing Natural Numbers Prompt Students found a need to sum the numbers 1 to n. One student offered a formula, but was not sure if he remembered it correctly. n(n +1) / 2 Students wondered if this would always be a natural number. A few mathematical foci • When n is a natural number, (n+1) / 2 is also a natural number. • Strategic choices for pair-wise grouping of numbers is critical to the development of the general formula. • The first n natural numbers form an arithmetic sequence. • Geometric arrays can lead to the development of the formula. n

Framework Mathematical Knowledge for Teaching • Mathematical Proficiency • Mathematical Activity • Mathematical Work of Teaching

Mathematical Proficiency • • • Conceptual Understanding Procedural Fluency Strategic Competence Adaptive Reasoning Productive Disposition Historical and Cultural Knowledge

At secondary level Procedural Fluency: Knowing when and how to apply a procedure in typical settings Algorithms are more complicated, settings are somewhat varied. Productive Disposition: Tendency to notice and apply mathematics in the world around us Mathematical applications are verging on modeling rather than solely recognizing or associating.

At secondary level Adaptive Reasoning: Adjust to changes in assumptions and conventions More attention is paid to assumptions and their consequences. There is more overt consideration of conventions. Strategic competence: Generating, evaluating, and implementing problemsolving strategies Strategies are evaluated for their mathematical fidelity, rather than solely for the viability of the answers they generate.

Conceptual Understanding: Knowing “why” Every triangle is cyclic. Every regular polygon is cyclic.

Historical and Cultural Knowledge Awareness of how people from various times and culture conceptualize and express mathematical ideas E. g. , The story of Gauss and the sum of the natural numbers from 1 to 100. 1 + 2 + 3 + … + 98 + 99 + 100 + 99 + 98 + … + 3 + 2 + 1 Sum = (100)(101)/2

Historical and Cultural Knowledge E. g. , The Japanese theorem for cyclic polygons states that no matter how we triangulate a cyclic polygon, the sum of the inradii is constant.

Mathematical Activity • Mathematical Noticing • Mathematical Reasoning • Mathematical Creating • Integrating Strands of Mathematical Activity

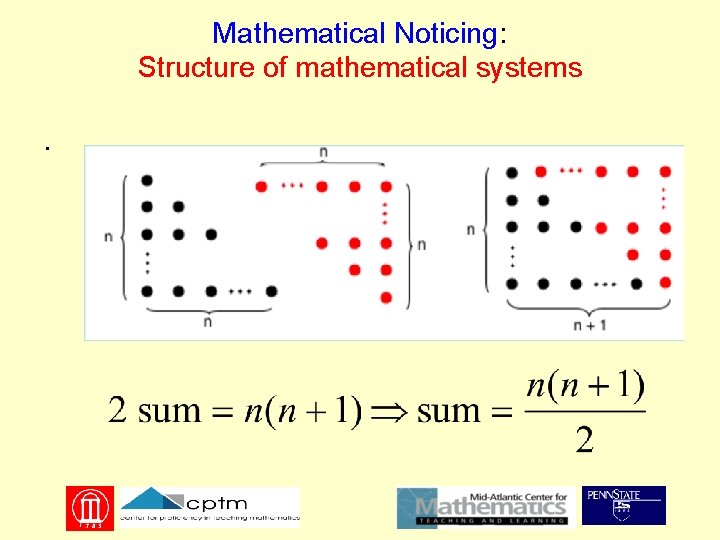
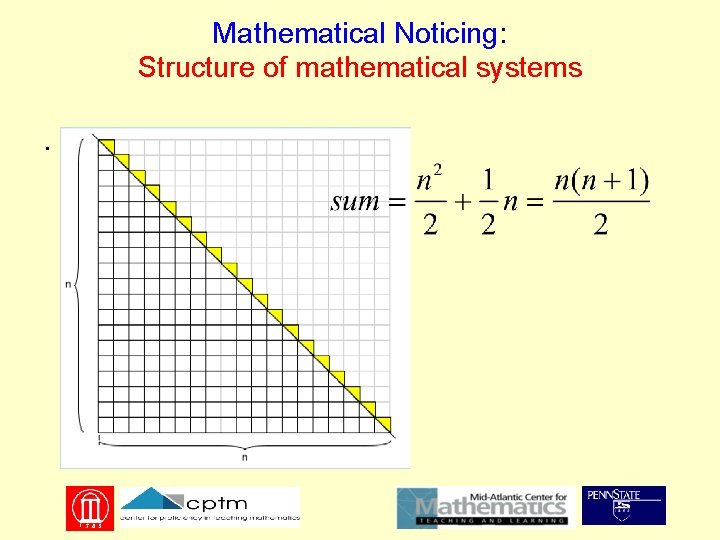
Mathematical Noticing Structure of mathematical systems Symbolic form Form of an argument Connections within and outside of mathematics

Summing Natural Numbers Prompt Students found a need to sum the numbers 1 to n. One student offered a formula, but was not sure if he remembered it correctly. n(n +1) / 2 Students wondered if this would always be a natural number. A few mathematical foci • When n is a natural number, (n+1) / 2 is also a natural number. • Strategic choices for pair-wise grouping of numbers is critical to the development of the general formula. • The first n natural numbers form an arithmetic sequence. • Geometric arrays can lead to the development of the formula. n

Mathematical Noticing: Structure of mathematical systems The set of natural numbers from 1 to n is an ordered sequence. Symmetry and the ordered nature of the sequence allow for rearrangements that facilitate finding a sum. Under any rearrangement, the cardinality and the sum of the elements remains the same.

Mathematical Noticing: Structure of mathematical systems .

Mathematical Noticing: Structure of mathematical systems .

Mathematical Noticing: Structure of mathematical systems .

Mathematical Noticing: Structure of mathematical systems .

Mathematical Reasoning • Justifying/Proving • Reasoning when conjecturing and generalizing • Constraining and extending

Mathematical Reasoning Constraining and extending We have looked at the sum of the first n natural numbers. What is the sum of the squares of the first n natural numbers? What is the sum of the kth powers of the first n natural numbers?

Circumscribing Polygons Prompt In a geometry class, after a discussion about circumscribing circles about triangles, a student asked, “Can you circumscribe a circle about any polygon? ” A few mathematical foci • Every triangle is cyclic. This fact is core to establishing a condition for other polygons to be cyclic. • A convex quadrilateral in a plane is cyclic if and only if its opposite angles are supplementary. • Every planar regular polygon is cyclic. However, not every cyclic polygon is regular.

Mathematical Reasoning Constraining and extending Regular polygons are cyclic. What are the conditions under which non-regular polygons are cyclic?

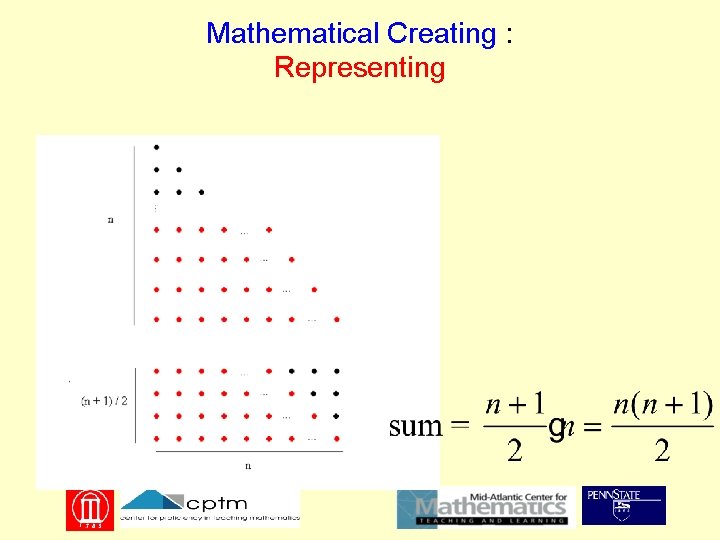
Mathematical Creating • Representing • Defining • Modifying/transforming/manipul ating

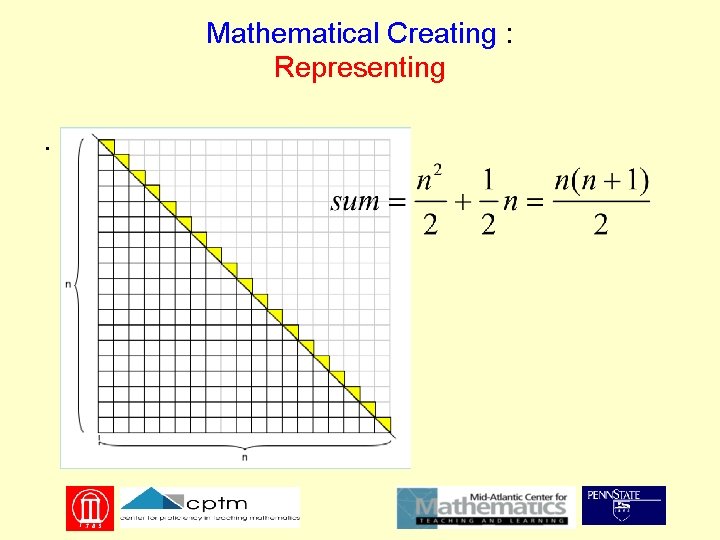
Mathematical Creating : Representing .

Mathematical Creating : Representing .

Mathematical Work of Teaching Teachers of secondary mathematics need the mathematical knowledge to be able to: • know and do mathematics themselves • facilitate their students’ development of mathematical knowledge

Mathematical Work of Teaching • Analyze mathematical ideas • Access and understand the mathematical thinking of students • Know and use the curriculum • Assess the mathematical proficiency of learners • Reflect on the mathematics of practice

Analyze mathematical ideas Mathematics is dense, often succinct, elegant, but teachers need to see behind the elegant product. Teachers need mathematical knowledge that helps them: • Probe; pull apart; unpack; dissect • Recognize conventions vs. core ideas • Understand the structure of mathematics

Analyze mathematical ideas Probe; pull apart; unpack; dissect What is an inverse? (operation & domain required) Types of inverses (additive, multiplicative, function) Conventions: notation (-1) operation for inverse function Strategies and rationale for finding inverse What is a function? (Need to restrict the domain)

Access and understand the mathematical thinking of students Students often express ideas in vague ways with imprecise terms. Teachers need mathematical knowledge that helps them: • Find key mathematical ideas within the students’ thinking; • See important mathematics within misconceptions; and • Understand the role of mathematical rigor.

Access and understand the mathematical thinking of students Find key mathematical ideas within the students’ thinking Students found a need to sum the numbers 1 to n. n(n +1) / 2 Students wondered if this would always be a natural number. Odd number/2 ≠ integer Why is n(n+1) always even? • If n is even, n+1 is odd • If n is odd, n +1 is even • Even x odd = even Why are even numbers 2 n? Odd numbers 2 n +1? What about (n 2 + n)/2?

Know and use the curriculum Curricula help to organize mathematical ideas. Teachers need mathematical knowledge that helps them: • Understand the mathematical scope and sequence in the curricula so it can be used or modified (know the flow); • Know how concepts are related or build on each other; and • Provide rationales for mathematical ideas.

Assess the mathematical knowledge of learners Assessing mathematical knowledge is uncovering understanding as well as misconception. Teachers need mathematical knowledge that helps them: • Assess more than procedural knowledge; • Identify the key concepts within problems or exercises; and • Ask formative and summative questions.

Assess the mathematical knowledge of learners Assess more than procedural knowledge There are 49 even numbers from 1 to 99. The mean of 48 of these numbers is. Which even number was not included in the calculating of this mean? From Taiwan’s May 2009 Basic Competency Test, as reported by Lo & Tsai in MTMS, March 2011.

Reflect on the mathematics of practice Revisiting mathematical ideas after a lesson or unit can provide new mathematical insights. Teachers need mathematical knowledge that helps them: • Recognize assignments that hide, distort or illuminate the mathematics; • Understand cultural factors that enhance or detract from the mathematics. (e. g. , vocabulary, contexts or problems); and • Recognize implicit mathematical ideas that need explanation? (e. g. , domain, convention, orientation of drawing)

Reflect on the mathematics of practice Recognize implicit mathematical ideas that need explanation? (e. g. , domain, convention, orientation) Can a linear equation have neither an x-intercept nor a y-intercept? A teacher asked her students to sketch the graph of A student responded, “That’s impossible! You can’t take the square root of a negative number!”

Framework Mathematical Knowledge for Teaching • Mathematical Proficiency • Mathematical Activity • Mathematical Work of Teaching

This presentation is based upon work supported by the Center for Proficiency in Teaching Mathematics and the National Science Foundation under Grant No. 0119790 and the Mid-Atlantic Center for Mathematics Teaching and Learning under Grant Nos. 0083429 and 0426253. Any opinions, findings, and conclusions or recommendations expressed in this presentation are those of the presenter(s) and do not necessarily reflect the views of the National Science Foundation.

Question 1 What is the role of mathematical actions in mathematical knowledge for teaching at the secondary level and how can this be built into their formal mathematical background?

Question 2 How could we develop and measure mathematical knowledge that enables the work of teaching?

Questions What is the role of mathematical actions in mathematical knowledge for teaching at the secondary level and how can this be built into their formal mathematical background? How could we develop and measure mathematical knowledge that enables the work of teaching?