6 Connections for Riemannian Manifolds and Gauge Theories

















![since [ U, V ] = 0 → λμ = ‘area’ of loop since [ U, V ] = 0 → λμ = ‘area’ of loop](https://slidetodoc.com/presentation_image_h/33543bd02f1f6a69d9e8b20abc652154/image-18.jpg)




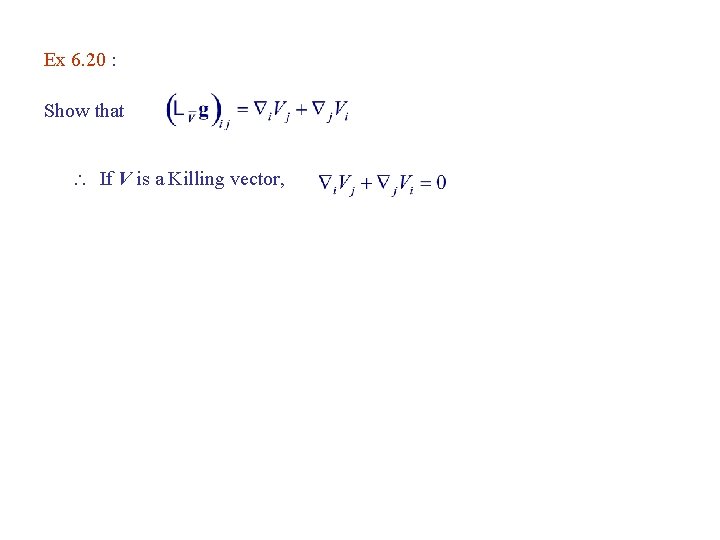








- Slides: 31

6. Connections for Riemannian Manifolds and Gauge Theories 6. 1 6. 2 6. 3 6. 4 6. 5 6. 6 6. 7 6. 8 6. 9 6. 10 6. 11 6. 12 6. 13 6. 14 6. 15 Introduction Parallelism on Curved Surfaces The Covariant Derivative Components: Covariant Derivatives of the Basis Torsion Geodesics Normal Coordinates Riemann Tensor Geometric Interpretation of the Riemann Tensor Flat Spaces Compatibility of the Connection with Volume- Measure or the Metric Connections The Affine Connection and the Equivalence Principle Connections & Gauge Theories: The Example of Electromagnetism Bibliography

6. 1. Introduction Affine connection → Shape & curvature. Gauge connection : Gauge theory. Connections are not part of the differential structure of the manifold. Amount of added structure: Volume element < Connection < Metric

6. 2. Parallelism on Curved Surfaces There is no intrinsic parallelism on a manifold. Example: Parallelism on S 2. Parallel transport = Moving a vector along a curve without changing its direction Direction of V at C depends on the route of parallel transport. → Absolute parallelism is meaningless. Affine connection defines parallel transport.

6. 3. The Covariant Derivative Let C be a curve on M with tangent At point P, pick a vector An affine connection then allows us to define a vector field V along C by parallel transport. The covariant derivative U along U is defined s. t. V is parallel transported along C. Let W be a vector defined everywhere on C. Then where W (P →Q ) is W(P) parallel-transported to Q = C(λ+δλ ).

Reminder: Lie dragging W along U requires the congruences of U & W around C. → LUW requires U & W be defined in neighborhood of C. Parallel transporting W along U requires only values of U & W on C. → UW requires only U & W be defined on C. Compatibility with the differential structure requires the covariant derivative to be a derivation (it satisfies the Leibniz rule) and additive in U. Thus Setting A, B = tensors we have

Under a change of parametrization λ → μ : With we have Combining with the additivity we have where f, g are functions. UW is a vector → the gradient W is a (11) tensor s. t. (see Ex 6. 1) Caution: itself is not a tensor since its not linear:

6. 4. Components: Covariant Derivatives of the Basis Any tensor can be expressed as a linear combination of basis tensors. The basis tensors for V are = vector Γkj i = Affine connection coefficients. = Christoffel symbols for a metric connection Thus, → where

The parallel transport of V is then given by Ex. 6. 6

6. 5. Torsion A connection is symmetric iff In a coordinate basis, a connection is symmetric iff The torsion T is defined by → T = 0 for symmetric connections T is a (12) tensor (Ex. 6. 9) The symmetric part of Γ is defined as Torsion is usually neglected in most theories. Ex. 6. 11 (Ex. 6. 8 )

6. 6 Geodesics A geodesic parallel transport its own tangent U, i. e. , ( Geodesic eq. ) Setting [ Geodesic = x i (λ) ] we get and The geodesic eq. is invariant under the linear transform λ→ a λ + b. λ is therefore an affine parameter. (see Ex. 6. 12) Only symmetric part of Γ contributes to the geodesic eq. → Geodesics are independent of torsion.

Geometric effects of torsion : Let U be the tangent at P of a geodesic C. Let RP be the (n 1)-D subspace of TP(M) consisting of vectors lin. indep. of U. Construct a geodesic through P with tangent ξ RP. Using Γ(S) , parallel transport U along ξ a small parameter distance εto point Q, i. e. , (S) ξ U = 0. Construct another geodesic C with tangent U through Q. C will be roughly parallel to C. A congruence of geodesics ‘parallel’ to U can be constructed around P in this manner. ξ can now be transported along U in 2 ways: • Parallel transport • Lie dragging

By design: Since we have By definition (§ 6. 5), the torsion T is given by U i ξj both sides gives → If ξ is parallel transported along U, → since i. e. , the parallel transported ξ is ‘twisted’ by the torsion along the geodesics.

6. 7. Normal Coordinates Each vector U TP(M) defines a unique geodesic CU (λ) with tangent U at P. A point Q near P can be associated with the unique vector U TP(M) that moves P to Q by a parallel-transport of distance Δλ = 1 along CU (λ). The normal coordinates of Q , with P as the origin, are defined as the components { U j } of U wrt some fixed basis of TP(M). Thus, a normal coordinate system is a 1 -1 map from M to TP(M) Rn. Since geodesics can cross in a curved manifold, different normal coordinate patches are required to cover it. The map from TP(M) to M is called the exponential map. It is well-defined even when the geodesics cross. A manifold is geodesically complete if the exponential map is defined for all U TP(M) and all P M. Useful property: Γijk |P = 0 in normal coordinates.

in normal coordinates Proof: Let Normal coordinates of Q a distance λ from P along geodesic CU(λ) are so that Q on CU(λ) → Geodesic eq. for CU(λ) in arbitrary coordinates is wrt normal coordinates {xi} , on CU(λ). Q on CU(λ) i. e. Since this must be satisfied by arbitrary U(P), we must have Reminder: In for Q P.

6. 8. Riemann Tensor The Riemann tensor R is defined by Its components are or R is a (13) tensor because it is a multiplicative operator containing no differential operations on its arguments : f = function ( Ex. 6. 13 ) In coordinate basis: ( Ex. 6. 14 a ) In non-coordinate basis with where

→ Rijkl is anti-symmetric in k & l, i. e. , Also Ex. 6. 14(c) Bianchi identities: In coordinate basis: The number of independent components of Rijkl in an n-D manifold is Ex. 6. 14(d) Caution: Other definitions (with different signs & index orderings) of R exist.

6. 9. Geometric Interpretation of the Riemann Tensor The parallel transport of A along U = d/dλ from P (0) to Q (λ) is for λ → 0 for finite λ Let V = d/dμ with [ U, V ] = 0 → λ & μ are good coordinates for a 2 -D subspace.
![since U V 0 λμ area of loop since [ U, V ] = 0 → λμ = ‘area’ of loop](https://slidetodoc.com/presentation_image_h/33543bd02f1f6a69d9e8b20abc652154/image-18.jpg)
since [ U, V ] = 0 → λμ = ‘area’ of loop

Geodesic Deviation Consider the congruence of geodesics CU defined by Let ξ be a vector field obtained by Lie dragging ξ|P along U, i. e. , (c. f. Ex. 6. 11) since

where i. e. , or since Geodesic deviation equation

6. 10. Flat Spaces Definition: A manifold is flat if Euclid’s axiom of parallelism holds, i. e. , The extensions of two parallel line segments never meet. Hence where U is any geodesics & ξ is Lie dragged by U. The sufficient condition for this to hold is R = 0, i. e. , R is a measure of the curvature of the manifold. Properties of a flat space: • Parallel transport is path-independent so that there is a global parallelism. • All TP(M) can be made identical (not merely isomorphic). • M can be identified with any TP(M). • Exponentiation can be extended throughout any simply-connected regions. Ex. 6. 16 : Polar coordinates in En with R 0

6. 11. Compatibility of the Connection with Volume- Measure or the Metric Compatibility issues arises when Γ & g or τ co-exist. E. g. , there are 2 ways to define the divergence of a vector field : via covariant derivative via volume n-form Compatibility requires V which is satisfied iff Ex 6. 17 a or Ex 6. 17 b E. g. , inner product should be invariant under parallel transport : g & Γ compatible iff i. e. , Ex 6. 18 metric connection
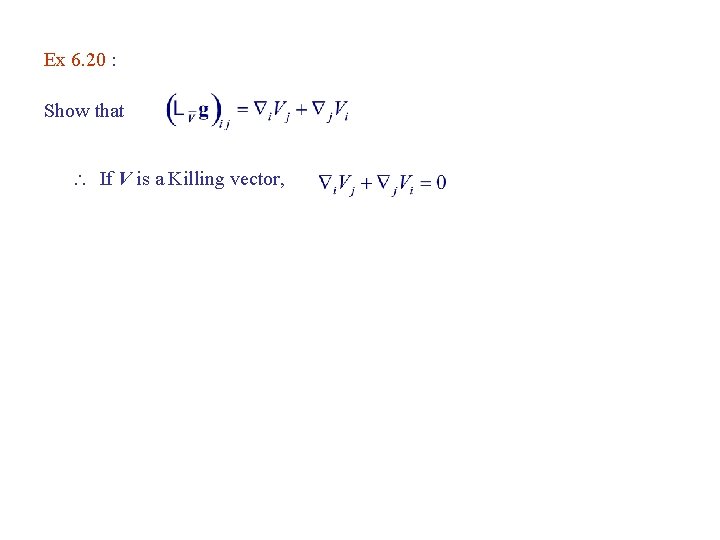
Ex 6. 20 : Show that If V is a Killing vector,

6. 12. Metric Connections Ex 6. 21 -2 : In normal coordinates → In which case, the number of independent components in R is

Ricci tensor : Ex 6. 23 Ricci scalar : Bianchi’s identities → Weyl tensor : Every contraction between the indices of Cijkl vanishes. Einstein tensor : Empty space : A geodesic is an extremum of arc length 6 independent eqs Ex 6. 24

6. 13. The Affine Connection and the Equivalence Principle Γijk = 0 for flat space in Cartesian coordinates. Γijk 0 for flat space in curvilinear coordinates. Principle of minimal coupling ( between physical fields & curvature of spacetime) = Strong principle of equivalence : Laws of physics take the same form in curved spacetime as in flat spacetime with curvilinear coordinates.

6. 14. Connections & Gauge Theories: The Example of Electromagnetism For an introduction to gauge theories, see Chaps 8 & 12 of I. D. Lawrie, “A unified grand tour of theoretical physics”, 2 nd ed. , Io. P (2002) Basic feature of gauge theories : Invariance under a group of gauge transformations. E. g. , electromagnetism: Variables: 1 -form A Gauge transformations: A→A+df

Consider a neutral scalar particle with mass m governed by Klein-Gordon eq. with If is a solution, so is Conserved probability current density , where is a constant. i. e. , the system is invariant under the gauge transformation Special relativity: Lorentz transformations (flat spacetime + Cartesian coord). Generalization to curvilinear coord introduces an affine connection. Relaxation to non-flat connections → gravitational effects (general relativity) Restriction to = constant is equivalent to flat space + Cartesian coord. Non-constant → EM forces.

General gauge transformation: Since e i is a point on the unit circle in the complex plane, the gauge transformation is a representation of the group U(1) on . The geometric structure is a fibre bundle ( called U(1)-bundle ) with base manifold M = Minkowski spacetime, and typical fibre = U(1) = unit circle in C. A gauge transformation is a cross-section of the U(1)-bundle. is not invariant under the general gauge transformation.

Remedy is to introduce a gauge-covariant derivative D s. t. & is invariant under the general gauge transformation. This is accomplished by a 1 -form connection A s. t. and so that Thus K. G. eq in an EM field with canonical momentum

Affine connection: preserves parallelism. Connection A : preserves phase of gradient under gauge transformation. Curvature introduced by an affine connection: Curvature introduced by A: → Gauge transformation: Faraday tensor or
 Gauge factor formula
Gauge factor formula Synventive hot runner systems
Synventive hot runner systems Pressure transducer basics
Pressure transducer basics Difference between bonded and unbonded strain gauge
Difference between bonded and unbonded strain gauge What is direct measuring instrument
What is direct measuring instrument Iso 22301 utbildning
Iso 22301 utbildning Typiska novell drag
Typiska novell drag Tack för att ni lyssnade bild
Tack för att ni lyssnade bild Returpilarna
Returpilarna Shingelfrisyren
Shingelfrisyren En lathund för arbete med kontinuitetshantering
En lathund för arbete med kontinuitetshantering Särskild löneskatt för pensionskostnader
Särskild löneskatt för pensionskostnader Tidbok för yrkesförare
Tidbok för yrkesförare Sura för anatom
Sura för anatom Förklara densitet för barn
Förklara densitet för barn Datorkunskap för nybörjare
Datorkunskap för nybörjare Tack för att ni lyssnade bild
Tack för att ni lyssnade bild Mall för debattartikel
Mall för debattartikel Magnetsjukhus
Magnetsjukhus Nyckelkompetenser för livslångt lärande
Nyckelkompetenser för livslångt lärande Påbyggnader för flakfordon
Påbyggnader för flakfordon Arkimedes princip formel
Arkimedes princip formel Svenskt ramverk för digital samverkan
Svenskt ramverk för digital samverkan Jag har nigit för nymånens skära text
Jag har nigit för nymånens skära text Presentera för publik crossboss
Presentera för publik crossboss Teckenspråk minoritetsspråk argument
Teckenspråk minoritetsspråk argument Bat mitza
Bat mitza Treserva lathund
Treserva lathund Mjälthilus
Mjälthilus Claes martinsson
Claes martinsson Centrum för kunskap och säkerhet
Centrum för kunskap och säkerhet Byggprocessen steg för steg
Byggprocessen steg för steg