3 lgebra y funciones 1 Polinomios 2 Identidades
3 Álgebra y funciones 1. Polinomios 2. Identidades notables 3. Resolución de ecuaciones de primer grado 4. Ecuaciones de segundo grado 5. Soluciones de una ecuación de segundo grado. Problemas 6. Sistemas de ecuaciones 7. Sucesiones 8. Progresiones aritméticas y geométricas 9. Funciones 10. Funciones afines 11. Funciones cuadráticas 12. Tasa de variación media Índice del libro

3 Álgebra y funciones 1. Polinomios SUMA Y RESTA DE POLINOMIOS Basta con sumar o restar los monomios que sean semejantes, es decir, que tengan la misma parte literal. EJEMPLO Restar

3 Álgebra y funciones 1. Polinomios PRODUCTO DE POLINOMIOS Hay que multiplicar cada monomio del primer polinomio por todos los monomios del segundo y luego agrupar todos los términos semejantes. EJEMPLO Multiplicar

3 Álgebra y funciones 1. Polinomios DIVISIÓN DE POLINOMIOS Para realizar la división de polinomios utilizaremos la «caja de división» : primero se colocan los polinomios en orden decreciente según sus grados y a continuación operamos de la misma manera que si de números se tratase. EJEMPLO Dividir

3 Álgebra y funciones 1. Polinomios FACTORIZACIÓN DE POLINOMIOS Cuando todos los términos de un polinomio comparten un factor común podemos expresar dicho polinomio como un producto entre esa parte común y la suma del resto de los factores. EJEMPLO Factorizar Sacamos factor común

3 Álgebra y funciones 2. Identidades notables IDENTIDADES NOTABLES Cuadrado de una suma Cuadrado de una resta Suma por diferencia
3 Álgebra y funciones 3. Resolución de ecuaciones de primer grado ECUACIONES DE PRIMER GRADO Resolver una ecuación es encontrar el valor o valores que, puestos en el lugar de la incógnita, cumplen lo que expresa la ecuación. Vamos a aprender a resolver ecuaciones de primer grado, que tienen un único número como solución. El método que vamos a usar para resolver ecuaciones es conseguir pasar de una ecuación complicada a una ecuación equivalente más sencilla. Para ello utilizaremos las siguientes propiedades: Regla de la suma Regla del producto Si sumamos o restamos una misma cantidad a los dos miembros de una ecuación, obtenemos una ecuación equivalente. Si multiplicamos o dividimos ambos miembros de una ecuación por un mismo número, obtenemos una ecuación equivalente.

3 Álgebra y funciones 3. Resolución de ecuaciones de primer grado PASOS A SEGUIR PARA RESOLVER UNA ECUACIÓN DE PRIMER GRADO 1. º Eliminar los paréntesis en ambos miembros y agrupar términos. 2. º Eliminar denominadores. 3. º Agrupar los términos con incógnita a un lado de la ecuación y los términos sin incógnita al otro. 4. º Despejar la incógnita dividiendo por el número adecuado. Al terminar, asegúrate de que no te has equivocado sustituyendo la solución en la ecuación y comprobando que se cumple la igualdad.

3 Álgebra y funciones 4. Ecuaciones de segundo grado ECUACIÓN DE SEGUNDO GRADO Grado de una ecuación: mayor número al que aparece elevada la incógnita. Para resolver una ecuación de segundo grado, lo primero que debemos conseguir es que tenga la siguiente forma: a, b y c son números reales La solución de esta ecuación es:

3 Álgebra y funciones 5. Soluciones de una ecuación de segundo grado. Problemas SOLUCIONES DE UNA ECUACIÓN DE SEGUNDO GRADO Discriminante positivo Discriminante nulo Discriminante negativo

3 Álgebra y funciones 6. Sistemas de ecuaciones SISTEMAS DE ECUACIONES Dos ecuaciones en las que aparecen las mismas incógnitas se denominan sistema de ecuaciones. Si las ecuaciones que forman el sistema son de primer grado, decimos que es un sistema de ecuaciones lineales. Métodos analíticos Se basan en obtener, mediante transformaciones algebraicas, una única ecuación para una de las dos incógnitas. Reducción Sustitución Igualación Método gráfico Consiste en representar ambas ecuaciones en un mismo sistema de coordenadas. Por ser ecuaciones de primer grado, su representación será una línea recta. La solución al sistema vendrá dada por el punto de corte de ambas rectas.
3 Álgebra y funciones 7. Sucesiones SUCESIONES Una sucesión es un conjunto ordenado de números, cada uno de los cuales recibe el nombre de término. De forma general, escribimos una sucesión como: Para definir una sucesión se pueden utilizar varios métodos: Descripción de términos Ley de recurrencia Término general Determinamos una sucesión mediante una propiedad que define sus términos y los listamos. Construimos cada término en relación a los anteriores. Partimos de un término inicial. Expresión que relaciona el valor de cada término con la posición que ocupa. EJEMPLO Números naturales pares 2, 4, 6, 8, 10, . . .

3 Álgebra y funciones 8. Progresiones aritméticas y geométricas PROGRESIONES ARITMÉTICAS Una progresión aritmética es una sucesión en la que cada término se obtiene sumando al anterior un número fijo. Este número fijo recibe el nombre de diferencia, d a 1 = primer término d = diferencia an = término general

3 Álgebra y funciones 8. Progresiones aritméticas y geométricas PROGRESIONES GEOMÉTRICAS Una progresión geométrica es una sucesión en la que cada término se obtiene multiplicando el anterior un número fijo. Este número fijo recibe el nombre de razón, r a 1 = primer término r = razón an = término general
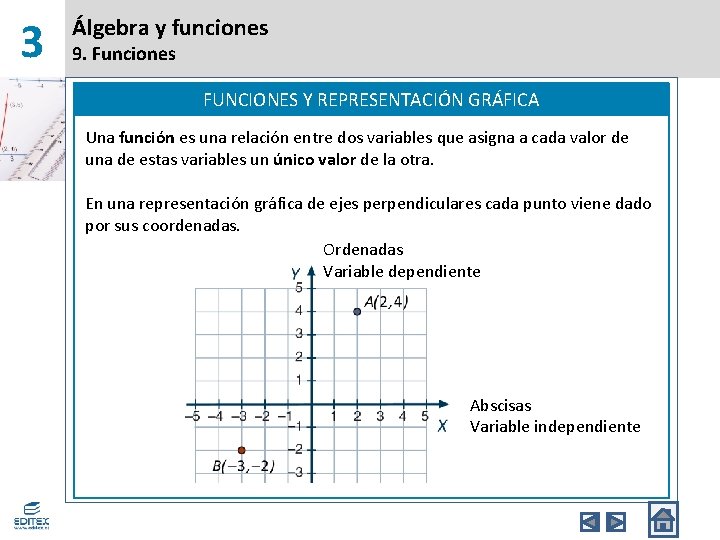
3 Álgebra y funciones 9. Funciones FUNCIONES Y REPRESENTACIÓN GRÁFICA Una función es una relación entre dos variables que asigna a cada valor de una de estas variables un único valor de la otra. En una representación gráfica de ejes perpendiculares cada punto viene dado por sus coordenadas. Ordenadas Variable dependiente Abscisas Variable independiente
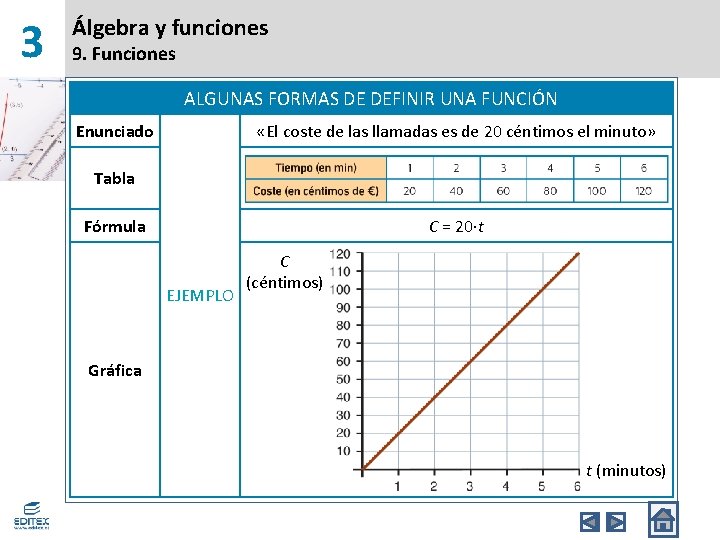
3 Álgebra y funciones 9. Funciones ALGUNAS FORMAS DE DEFINIR UNA FUNCIÓN Enunciado «El coste de las llamadas es de 20 céntimos el minuto» Tabla Fórmula C = 20∙t EJEMPLO C (céntimos) Gráfica t (minutos)
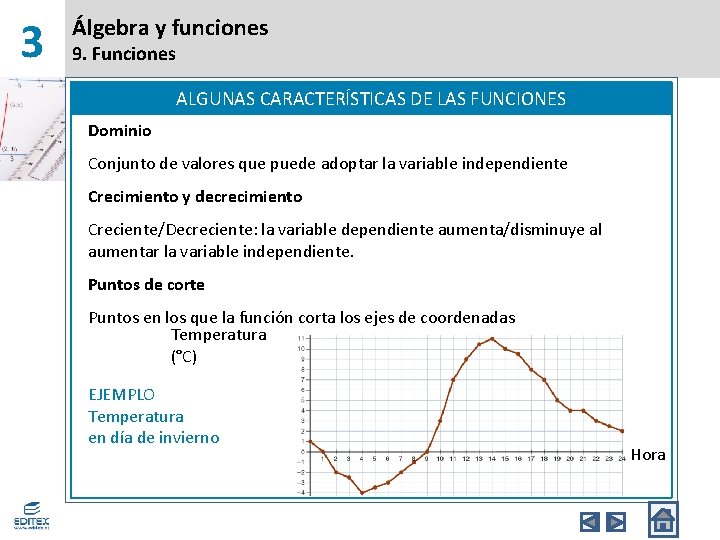
3 Álgebra y funciones 9. Funciones ALGUNAS CARACTERÍSTICAS DE LAS FUNCIONES Dominio Conjunto de valores que puede adoptar la variable independiente Crecimiento y decrecimiento Creciente/Decreciente: la variable dependiente aumenta/disminuye al aumentar la variable independiente. Puntos de corte Puntos en los que la función corta los ejes de coordenadas Temperatura (°C) EJEMPLO Temperatura en día de invierno Hora

3 Álgebra y funciones 10. Funciones afines FUNCIÓN AFÍN § La representación gráfica de una función afín es una recta. § Tiene una expresión algebraica de la forma: y = m∙x + n § A m se le denomina pendiente y nos indica la inclinación de la recta. § A n se le denomina ordenada en el origen y nos da el punto de corte de la recta con el eje vertical.
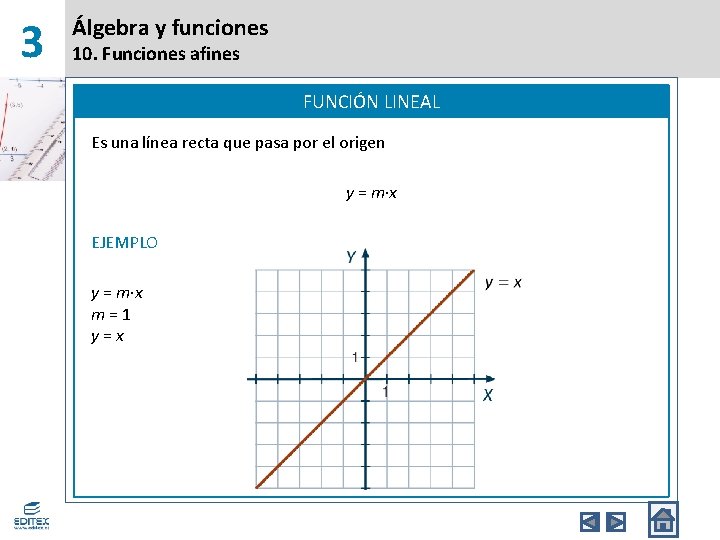
3 Álgebra y funciones 10. Funciones afines FUNCIÓN LINEAL Es una línea recta que pasa por el origen y = m∙x EJEMPLO y = m∙x m=1 y=x

3 Álgebra y funciones 11. Funciones cuadráticas FUNCIÓN CUADRÁTICA § Su forma general es y = a x 2 + b x + c § Su representación gráfica es una curva que recibe el nombre de parábola. § Vértice de la parábola § Puntos de corte con el eje x, horizontal, y = 0 y = a x 2 + b x + c = 0 § Puntos de corte con el eje y, vertical, y=c x=0 Punto (0, c)
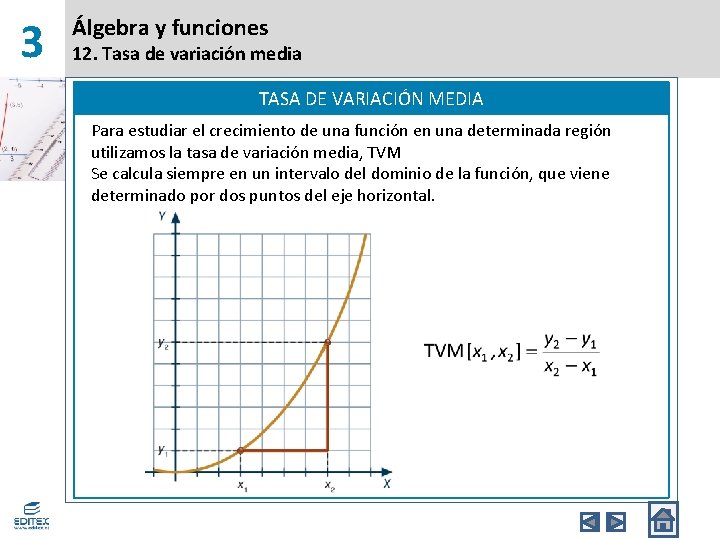
3 Álgebra y funciones 12. Tasa de variación media TASA DE VARIACIÓN MEDIA Para estudiar el crecimiento de una función en una determinada región utilizamos la tasa de variación media, TVM Se calcula siempre en un intervalo del dominio de la función, que viene determinado por dos puntos del eje horizontal.
- Slides: 21