1 JianJiun Ding National Taiwan University 723 531

1 丁建均 (Jian-Jiun Ding) National Taiwan University 辦公室：明達館 723室， 實驗室：明達館 531室 聯絡電話： (02)33669652 Major：Digital Signal Processing Digital Image Processing

Research Fields [A. Signal Analysis] (1) Time-Frequency Analysis (2) Fractional Fourier Transform 2 : the main topics I researched in recent years : the main topics I research before (3) Wavelet Transform (4) Eigenfunctions, Eigenvectors, and Prolate Spheroidal Wave Function (5) Signal Analysis (Cepstrum, Hilbert, CDMA) [B. Fast Algorithm] (6) Integer Transforms (7) Fast Algorithms (8) Number Theory, Haar Transform, Walsh Transform

3 [C. Applications of Signal Processing] (9) Optical Signal Processing (10) Acoustics (11) Bioinformatics [D. Image Processing] (12) Image Compression (13) Edge and Corner Detection (14) Pattern Recognition [E. Theories for Signal Processing] (15) Quaternion : the main topics I researched in recent years : the main topics I research before

1. Time-Frequency Analysis http: //djj. ee. ntu. edu. tw/TFW. htm Fourier transform (FT) Time-Domain Frequency Domain Some things make the FT not practical: (1) Only the case where t 0 t t 1 is interested. (2) Not all the signals are suitable for analyzing in the frequency domain. It is hard to analyze the signal whose instantaneous frequency varies with time. 4

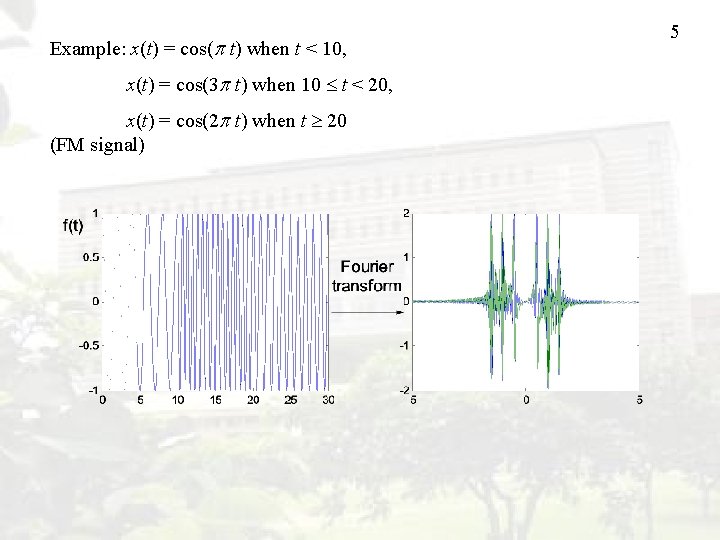
Example: x(t) = cos( t) when t < 10, x(t) = cos(3 t) when 10 t < 20, x(t) = cos(2 t) when t 20 (FM signal) 5

6 Instantaneous Frequency 瞬時頻率 If then the instantaneous frequency of f (t) are 其他瞬時頻率會隨時間而改變的例子 音樂，語音信號 Chirp Signal

7 Several Time-Frequency Distribution Short-Time Fourier Transform (STFT) with Rectangular Mask Gabor Transform avoid cross-term less clarity Wigner Distribution Function with cross-term high clarity Gabor-Wigner Transform (Proposed) avoid cross-term high clarity

8 Cohen’s Class Distribution where S Transform Hilbert-Huang Transform

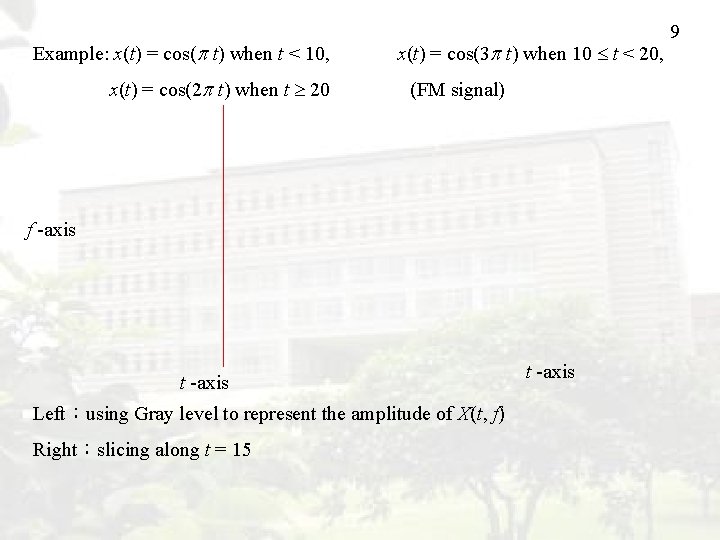
Example: x(t) = cos( t) when t < 10, x(t) = cos(2 t) when t 20 x(t) = cos(3 t) when 10 t < 20, (FM signal) f -axis t -axis Left：using Gray level to represent the amplitude of X(t, f) Right：slicing along t = 15 t -axis 9

Applications of Time-Frequency Analysis (1) Finding Instantaneous Frequency (2) Sampling Theory (3) Filter Design (4) Signal Decomposition (5) Modulation and Multiplexing (6) Electromagnetic Wave Propagation (7) Optics (8) Radar System Analysis (9) Random Process Analysis (10) Signal Identification (11) Acoustics (12) Biomedical Engineering (13) Spread Spectrum Analysis (14) System Modeling (15) Image Processing (16) Economic Data Analysis (17) Signal Representation (18) Data Compression 10

11 Conventional Sampling Theory Nyquist Criterion New Sampling Theory (1) t can vary with time (2) Number of sampling points == Area of time frequency distribution

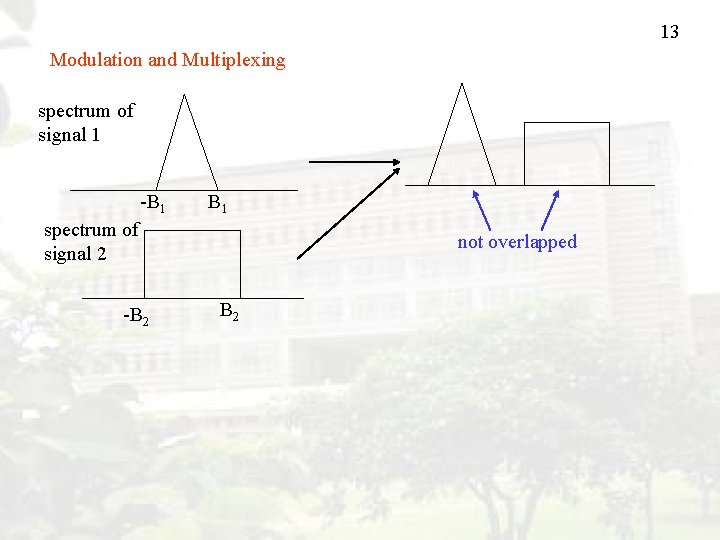
13 Modulation and Multiplexing spectrum of signal 1 -B 1 spectrum of signal 2 -B 2 not overlapped B 2

14 Improvement of Time-Frequency Analysis (1) Computation Time (2) Tradeoff of the cross term problem and clarification

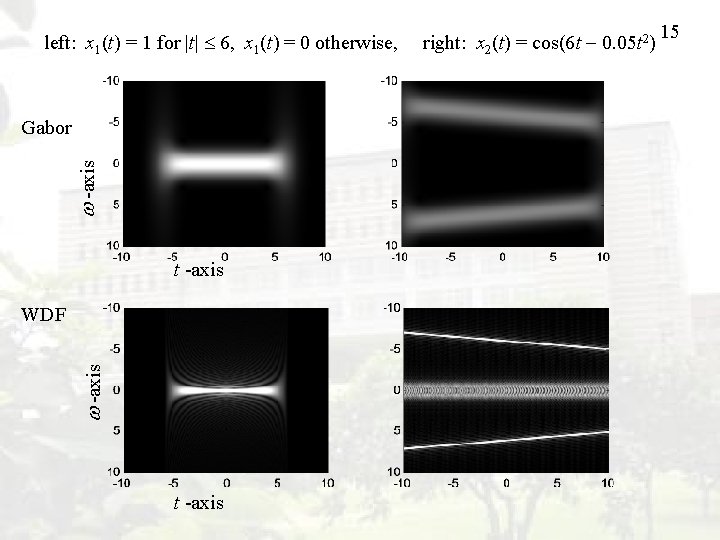
left: x 1(t) = 1 for |t| 6, x 1(t) = 0 otherwise, -axis Gabor t -axis WDF t -axis right: x 2(t) = cos(6 t 0. 05 t 2) 15

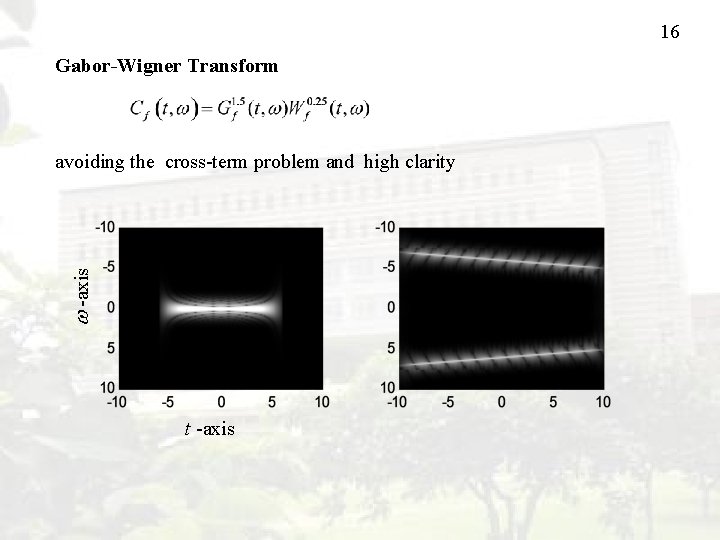
16 Gabor-Wigner Transform -axis avoiding the cross-term problem and high clarity t -axis

17 2. Fractional Fourier Transform Performing the Fourier transform a times (a can be non-integer) Fourier Transform (FT) generalization Fractional Fourier Transform (FRFT) , When = 0. 5 , the FRFT becomes the FT. = a/2

18 Fractional Fourier Transform (FRFT) , When = 0: = a/2. (identity) When = 0. 5 : When is not equal to a multiple of 0. 5 , the FRFT is equivalent to doing /(0. 5 ) times of the Fourier transform. when = 0. 1 doing the FT 0. 2 times; when = 0. 25 doing the FT 0. 5 times; when = /6 doing the FT 1/3 times;

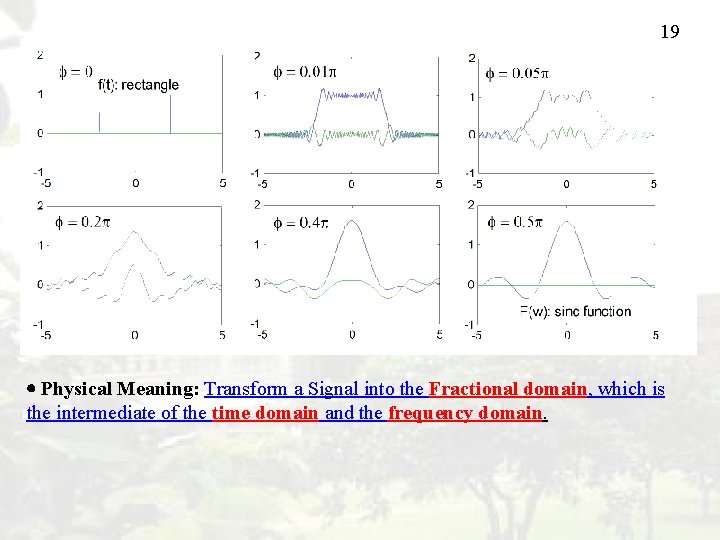
19 Physical Meaning: Transform a Signal into the Fractional domain, which is the intermediate of the time domain and the frequency domain.

Time domain Frequency domain fractional domain Modulation Shifting Modulation + Shifting Differentiation −j 2 f Differentiation and j 2 f Differentiation and −j 2 f is some constant phase 20

Why do we use the fractional Fourier transform? To solve the problems that cannot be solved by the Fourier transform Example: Filter Design Conventional filter design: x(t): input x(t) = s(t) (signal) + n(t) (noise) y(t): output (We want that y(t) s(t)) H( ): the transfer function of the filter. Filter design by the fractional Fourier transform (FRFT): (replace the FT and the IFT by the FRFTs with parameters and ) 21

When x(t) = triangular signal + chirp noise exp[j 0. 25(t 4. 12)2] 22

23 The Fourier transform is suitable to filter out the noise that is a combination of sinusoid functions exp(j 0 t). The fractional Fourier transform (FRFT) is suitable to filter out the noise that is a combination of higher order exponential functions exp[j(nk tk + nk-1 tk-1 + nk-2 tk-2 + ……. + n 2 t 2 + n 1 t)] For example: chirp function exp(jn 2 t 2) With the FRFT, many noises that cannot be removed by the FT will be filtered out successfully.

From the view points of Time-Frequency Analysis: (1) Wigner distribution function (WDF) [Ref 9] S. C. Pei and J. J. Ding, “Relations between the fractional operations and the Wigner distribution, ambiguity function, ” IEEE Trans. Signal Processing, v. 49, pp 1638 -1655, (2001). (2) Gabor transform [Ref 10] S. C. Pei and J. J. Ding, “Relations between Gabor Transforms and Fractional Fourier Transforms and Their Applications for Signal Processing, ” IEEE Trans. Signal Processing, vol. 55, no. 10, pp. 4839 -4850, Oct. 2007. 24

25 [Theorem] The FRFT with parameter is equivalent to the clockwise rotation operation with angle for Wigner distribution functions (or for Gabor transforms) FRFT = with angle The Gabor Transform for the FRFT of the rectangular function. = 0 (identity), /6 horizon: t-axis, vertical: f-axis 2 /6 /2 (FT) 4 /6 5 /6

26 Filter designed by the fractional Fourier transform 比較：Filter Designed by the Fourier transform f-axis Signal noise FRFT noise Signal FRFT t-axis cutoff line

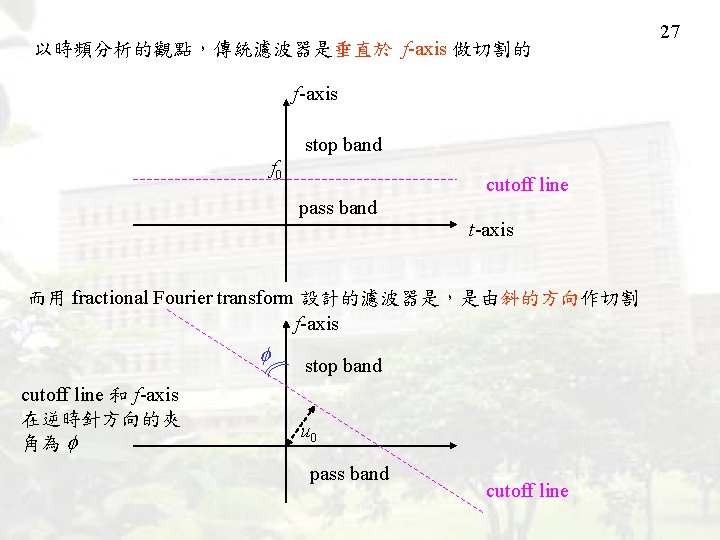
以時頻分析的觀點，傳統濾波器是垂直於 f-axis 做切割的 f-axis stop band f 0 cutoff line pass band t-axis 而用 fractional Fourier transform 設計的濾波器是，是由斜的方向作切割 f-axis cutoff line 和 f-axis 在逆時針方向的夾 角為 stop band u 0 pass band cutoff line 27

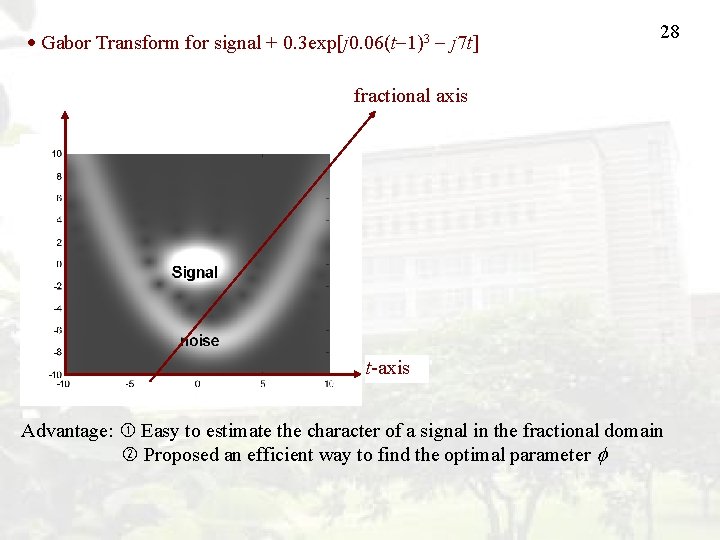
Gabor Transform for signal + 0. 3 exp[j 0. 06(t 1)3 j 7 t] 28 fractional axis t-axis Advantage: Easy to estimate the character of a signal in the fractional domain Proposed an efficient way to find the optimal parameter

29 In fact, all the applications of the Fourier transform (FT) are also the applications of the fractional Fourier transform (FRFT), and using the FRFT instead of the FT for these applications may improve the performance. Filter Design : developed by us improved the previous works Signal synthesis (compression, random process, fractional wavelet transform) Correlation (space variant pattern recognition) Communication (modulation, multiplexing, multiple-path problem) Sampling Solving differential equation Image processing (asymmetry edge detection, directional corner detection) Optical system analysis (system model, self-imaging phenomena) Wave propagation analysis (radar system, GRIN-medium system)

Invention: 30 [Ref 1] N. Wiener, “Hermitian polynomials and Fourier analysis, ” Journal of Mathematics Physics MIT, vol. 18, pp. 70 -73, 1929. Re-invention [Ref 2] V. Namias, “The fractional order Fourier transform and its application to quantum mechanics, ” J. Inst. Maths. Applics. , vol. 25, pp. 241265, 1980. Introduction for signal processing [Ref 3] L. B. Almeida, “The fractional Fourier transform and time-frequency representations, ” IEEE Trans. Signal Processing, vol. 42, no. 11, pp. 30843091, Nov. 1994. Recent development Pei, Ding (after 1995), Ozaktas, Mendlovic, Kutay, Zalevsky, etc.

Extension 1: Discrete Fractional Fourier Transform 31 Type 1: Sampling Form Complexity: 2 N + Nlog 2 N [Ref 4] S. C. Pei and J. J. Ding, “Closed form discrete fractional and affine Fourier transforms, ” IEEE Trans. Signal Processing, vol. 48, no. 5, pp. 1338 -1353, May 2000. Type 2: Eigenfunction Decomposition Form E: eigenvectors of the DFT (many choices), D: eigenvalues [Ref 5] S. C. Pei, W. L. Hsue, and J. J. Ding, “Discrete fractional Fourier transform based on new nearly tridiagonal commuting matrices, ” accepted by IEEE Trans. Signal Processing.

32 Extension 2: Fractional Cosine Transform [Ref 6] S. C. Pei and J. J. Ding, “Fractional, canonical, and simplified fractional cosine, sine and Hartley transforms, ” IEEE Trans. Signal Processing, vol. 50, no. 7, pp. 1611 -1680, Jul. 2002. Extension 3: N-D Affine Generalized Fractional Fourier Transform [Ref 7] S. C. Pei and J. J. Ding, “Two-dimensional affine generalized fractional Fourier transform, ” IEEE Trans. Signal Processing, vol. 49, no. 4, pp. 878 -897, Apr. 2001.

Extension 4: Simplified Fractional Fourier Transform 33 (easier for digital implementation) (easier for optical implementation) [Ref 8] S. C. Pei and J. J. Ding, “Simplified fractional Fourier transforms, ” J. Opt. Soc. Am. A, vol. 17, no. 12, pp. 2355 -2367, Dec. 2000.

My works related to the fractional Fourier transform (FRFT) Extensions: Discrete fractional Fourier transform Fractional cosine, and Hartley transform, Two-dimensional form, N-D form, Simplified fractional Fourier transform Fractional Hilbert transform, Foundation theory: relations between the FRFT and the well-known timefrequency analysis tools (e. g. , the Wigner distribution function and the Gabor transform) Applications: sampling, encryption, corner and edge detection, selfimaging Solving the problem for implementation phenomena, bandwidth saving, multiple-path problem analysis 34

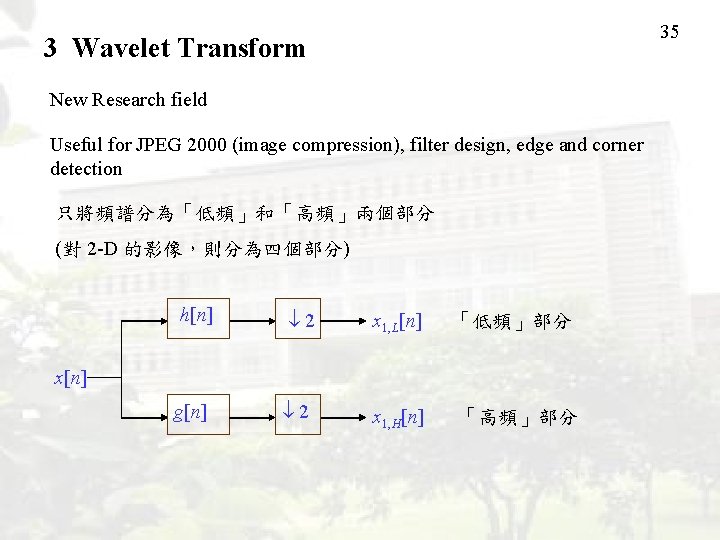
35 3 Wavelet Transform New Research field Useful for JPEG 2000 (image compression), filter design, edge and corner detection 只將頻譜分為「低頻」和「高頻」兩個部分 (對 2 -D 的影像，則分為四個部分) h[n] 2 x 1, L[n] 「低頻」部分 g[n] 2 x 1, H[n] 「高頻」部分 x[n]

36 The result of the wavelet transform for a 2 -D image lowpass for x lowpass for y highpass for x lowpass for y highpass for y

37 6. Integer Transform Conversion Integer Transform: The discrete linear operation whose entries are summations of 2 k. , ak = 0 or 1 or , C is an integer.

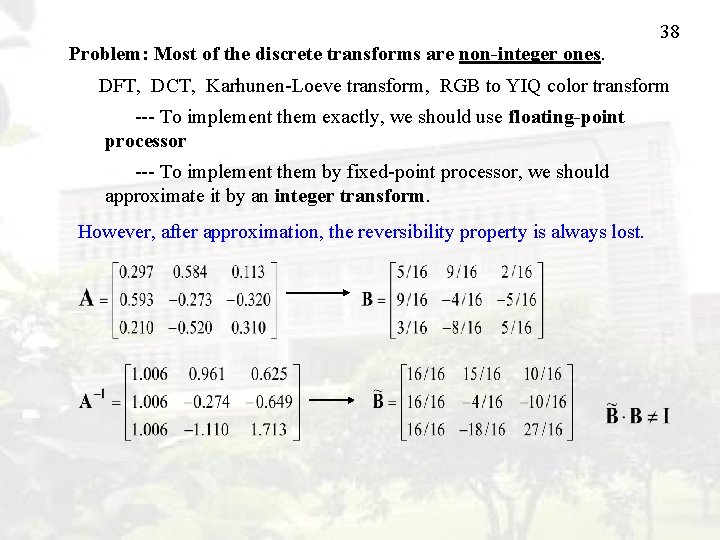
38 Problem: Most of the discrete transforms are non-integer ones. DFT, DCT, Karhunen-Loeve transform, RGB to YIQ color transform --- To implement them exactly, we should use floating-point processor --- To implement them by fixed-point processor, we should approximate it by an integer transform. However, after approximation, the reversibility property is always lost.

39 [Integer Transform Conversion]: Converting all the non-integer transform into an integer transform that achieve the following 6 Goals: A, A-1: original non-integer transform pair, (Goal 1) Integerization (Goal 2) Reversibility , B, B : integer transform pair , bk and b k are integers. . (Goal 3) Bit Constraint The denominator 2 k should not be too large. (Goal 4) Accuracy B A, (Goal 5): Less Complexity (Goal 6) Easy to Design B A-1 (or B A, B -1 A-1)

40 Development of Integer Transforms: (A) Prototype Matrix Method (Partially my work) (suitable for 2, 4, 8 and 16 -point DCT, DST, DFT) (B) Lifting Scheme (suitable for 2 k-point DCT, DST, DFT) (C) Triangular Matrix Scheme (suitable for any matrices, satisfies Goals 1 and 2) (D) Improved Triangular Matrix Scheme (My works) (suitable for any matrices, satisfies Goals 1 ~ 6)

Basic idea of the triangular matrix scheme: Any matrix can be decomposed as A = PDLUSQ P, Q: permuting matrices, D: diagonal matrix L: lower triangular matrix, U: upper triangular matrix, S: One row lower triangular matrix Problem: The number of bits is increased (due to 3 triangular matrices) Number of bit tradeoff Accuracy The number of time cycles is increased (due to 3 triangular matrices) How to find the optimal one 41

42 References Related to the Integer Transform [Ref. 1] W. K. Cham, “Development of integer cosine transform by the principles of dynamic symmetry, ” Proc. Inst. Elect. Eng. , pt. 1, vol. 136, no. 4, pp. 276 -282, Aug. 1989. [Ref. 2] S. C. Pei and J. J. Ding, “The integer Transforms analogous to discrete trigonometric transforms, ” IEEE Trans. Signal Processing, vol. 48, no. 12, pp. 3345 -3364, Dec. 2000. [Ref. 3] T. D. Tran, “The bin. DCT: fast multiplierless approximation of the DCT, ” IEEE Signal Proc. Lett. , vol. 7, no. 6, pp. 141 -144, June 2000. [Ref. 4] P. Hao and Q. Shi. , “Matrix factorizations for reversible integer mapping, ” IEEE Trans. Signal Processing, vol. 49, no. 10, pp. 2314 -2324, Oct. 2001. [Ref. 5] S. C. Pei and J. J. Ding, “Reversible Integer Color Transform with Bit-Constraint, ” accepted by ICIP 2005. [Ref. 6] S. C. Pei and J. J. Ding, “Improved Integer Color Transform, ” in preparation.

43 9. Optical Signal Processing and Fractional Fourier Transform lens, (focal length = f) free space, (length = z 1) free space, (length = z 2) f = z 1 = z 2 Fourier Transform f z 1, z 2 but z 1 = z 2 Fractional Fourier Transform f z 1 z 2 Fractional Fourier Transform multiplied by a chirp

45 11. Discrete Correlation Algorithm for DNA Sequence Comparison [Reference] S. C. Pei, J. J. Ding, and K. H. Hsu, “DNA sequence comparison and alignment by the discrete correlation algorithm, ” submitted. There are four types of nucleotide in a DNA sequence: adenine (A), guanine (G), thymine (T), cytosine (C) Unitary Mapping bx[ ] = 1 bx[ ] = j if x[ ] = ‘A’, if x[ ] = ‘G’, bx[ ] = 1 bx[ ] = j if x[ ] = ‘T’, if x[ ] = ‘C’. y = ‘AACTGAA’, by = [1, 1, j, 1, j, 1, 1].

46 Discrete Correlation Algorithm for DNA Sequence Comparison For two DNA sequences x and y, if where Then there are s[n] nucleotides of x[n+ ] that satisfies x[n+ ] = y[ ]. Example: x = ‘GTAGCTGAAC’, y = ‘AACTGAA’, . x= ‘GTAGCTGAAC’, y (shifted 7 entries rightward) = ‘AACTGAA’.

47 Example: x = ‘GTAGCTGAAC’, y = ‘AACTGAA’, s[n] = . Checking: x= y= ‘GTAGCTGAAC’, ‘AACTGAA’. (no entry match) x= ‘GTAGCTGAAC’, y = (shifted 2 entries rightward) ‘AACTGAA’. (6 entries match) x= ‘GTAGCTGAAC’, y (shifted 7 entries rightward) = ‘AACTGAA’. (7 entries match)

48 Advantage of the Discrete Correlation Algorithm: ---The complexity of the conventional sequence alignments is O(N 2) ---For the discrete correlation algorithm, the complexity is reduced to O(N log 2 N) or O(N log 2 N + b 2) b: the length of the matched subsequences Experiment: Local alignment for two 3000 -entry DNA sequences Using conventional dynamic programming Computation time: 87 sec. Using the proposed discrete correlation algorithm: Computation time: 4. 13 sec.

49 12. Image Compression Conventional JPEG method: Separate the original image into many 8*8 blocks, then using the DCT to code each blocks. DCT: discrete cosine transform PS: 感謝 2008年畢業的黃俊德同學

50 JPEG 是當前最普及的影像壓縮格式。 問題：壓縮率高的時候，會產生 blocking effect Compression ratio = 53. 4333 RMSE = 10. 9662

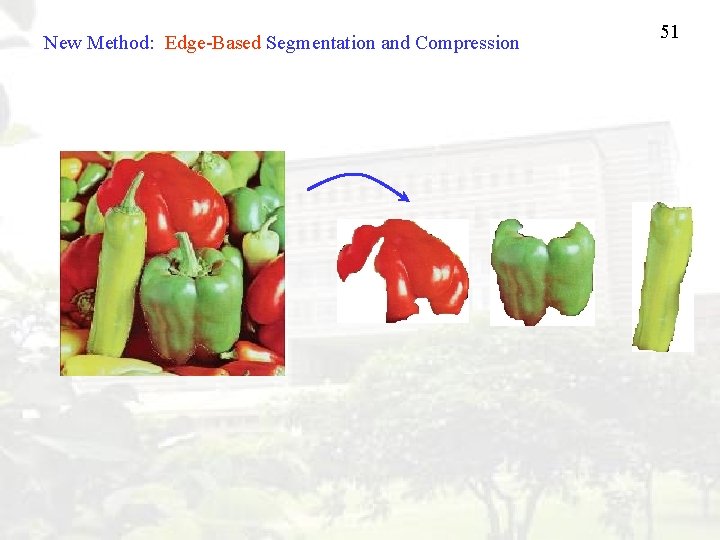
New Method: Edge-Based Segmentation and Compression 51

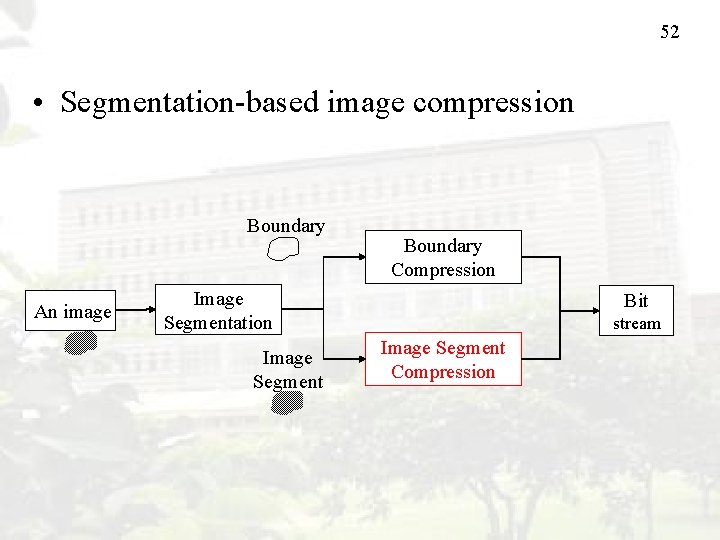
52 • Segmentation-based image compression Boundary An image Boundary Compression Image Segmentation Image Segment Bit stream Image Segment Compression

53 Original Image An 100 x 100 image By JPEG Bytes: 1295, RMSE: 2. 39 By Proposed Method Bytes: 456, RMSE: 2. 54

13. Edge and Corner Detection Why should we perform edge and corner detection? Segmentation Compression 54

55 Simplest way for edge detection: differentiation

by differentiation 56

57 Doing difference x[n] x[n 1] = x[n] (convolution) with h[n] = 1 for n = 0, h[n] = -1 for n = 1, h[n] = 0 otherwise. Other ways for edge detection: convolution with a longer odd function x[n]

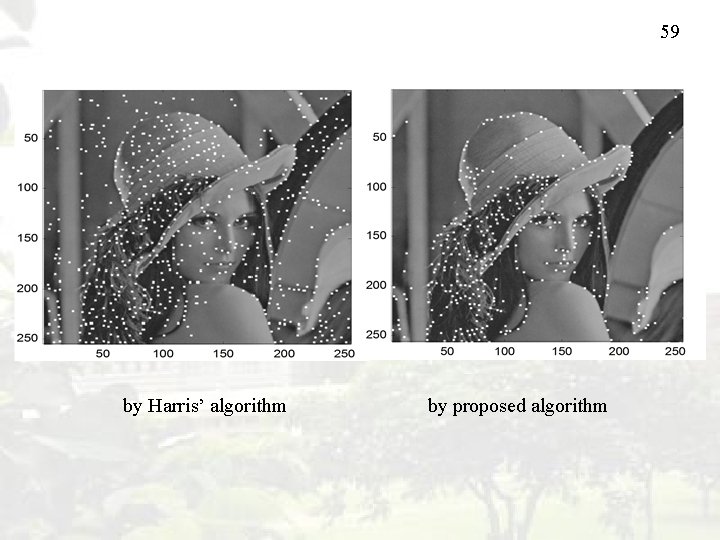
58 Corner Detection Corner: the edge of an edge +( + /2) + Conventional Algorithm: Observing the variation along x-axis and y-axis, Proposed Algorithm: Observing the variation along + axis, -axis, +( + /2)-axis and ( + /2)-axis, - ( + /2)

59 by Harris’ algorithm by proposed algorithm

14. Pattern Recognition 應用很廣： security, identification ………… 最簡單的方法： matched filter 但技術上的問題頗多………. scaling shadow rotation partially distortion 其他的方法： 特徵拮取 60

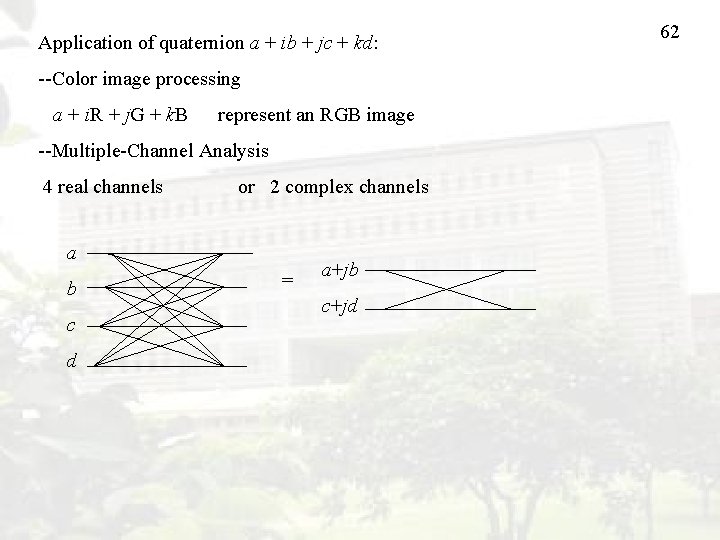
61 15. Quaternion 翻譯成“四元素”，Generalization of complex number Complex number: a + ib i 2 = 1 real part imaginary part Quaternion: a + ib + jc + kd real part i 2 = j 2 = k 2 = 1 3 imaginary parts [Ref 18] S. C. Pei, J. J. Ding, and J. H. Chang, “Efficient implementation of quaternion Fourier transform, ” IEEE Trans. Signal Processing, vol. 49, no. 11, pp. 2783 -2797, Nov. 2001. [Ref 19] S. C. Pei, J. H. Chang, and J. J. Ding, “Commutative reduced biquaternions for signal and image processing, ” IEEE Trans. Signal Processing, vol. 52, pp. 2012 -2031, July 2004.

Application of quaternion a + ib + jc + kd: --Color image processing a + i. R + j. G + k. B represent an RGB image --Multiple-Channel Analysis 4 real channels or 2 complex channels a b c d = a+jb c+jd 62