YiFei PU College of Computer Science and Software

分数阶智能信号处理 在《计算法学》中的应用 蒲亦非（Yi-Fei PU） 四川大学计算机学院 & 软件学院 College of Computer Science, and Software Engineering, Sichuan University

CV 1 3 Idea 2 3 Theory and applications

CV 1 3 Idea 2 3 Theory and applications

CV 蒲亦非 （Yi-Fei PU） Ph. D. , Postdoctor, Full Professor, and Doctoral Supervisor with the College of Computer Science, and Software Engineering, Sichuan University I am elected into the Thousand Talents Program of Sichuan Province. I have published about 40 papers indexed by SCI in journals such as IEEE Transactions on Image Processing, IEEE Transactions on Neural Networks and Learning Systems, Mathematic Methods in Applied Sciences, and Science China Information Sciences, etc. I hold 14 China Patents for Invention, as the first or single inventor.

CV 1 3 Idea 2 3 Theory and applications

Idea - Background In applied mathematics and mathematical analyses, fractional derivative is a derivative of any arbitrary order, real or plural. Even though the term fractional is a misnomer, it has been widely accepted for such a derivative for a long time. The concept of a fractional derivative is coined by the famous mathematician Leibniz in 1695 in his letter to L'Hôpital.

Idea - Background Nowadays, fractional calculus has become an important novel branch in mathematical analyses. The origin of fractional calculus was concurrent with that of integer-order calculus; however, until recently, the applications of fractional calculus were limited to mathematics. Fractional calculus appears to be a novel promising mathematical method for physical scientists and engineering technicians.

Idea - Background Fractional calculus extends the concepts of integer-order difference and Riemann sums. The fractional differential of a Heaviside function is non-zero, whereas its integer-order differential must be zero. The random variable in a physical process can be considered as the displacement of the random movement of particles.

Idea - Background The fractional calculus of various functions possesses an inherent characteristic—the fractional calculus of most functions is equal to a power series, and the fractional calculus of other functions is equal to the superposition or product of a certain function and a power function. This characteristic may hint at a significant changing law of nature.

Idea - Background Scientific study has shown that, nowadays, a fractionalorder or fractional dimensional approach is the best description for many natural phenomena. Promising results and ideas have demonstrated that fractional calculus can be an interesting and useful tool in many scientific fields such as diffusion processes, viscoelasticity theory, fractal dynamics, fractional control, signal processing, fractance, and image processing.

Idea - Background The application of fractional calculus to signal analysis and processing, specifically to image processing, is an emerging discipline of research, and few studies have been conducted in this area.

Idea - Background The properties of the fractional calculus of a signal are significantly different from those of its integer-order calculus. Fractional calculus has been hybridized with signal processing primarily owing to its inherent advantages of long-term memory and non-locality. Certain remarkable progress in the studies on fractional signal processing validates such systems as fractional dynamic systems, and also provides interesting and practical suggestions for future research.

Idea - Background For instance, in the fields of fractional-order adaptive control, pattern recognition, adaptive signal processing, and neural networks, the fractional-order extreme points of the quadratic energy norm are considerably different from the traditional integer-order extreme points such as the first-order stationary points.

Idea - Background For instance, in the fields of fractional-order adaptive control, pattern recognition, adaptive signal processing, and neural networks, the fractional-order extreme points of the quadratic energy norm are considerably different from the traditional integer-order extreme points such as the first-order stationary points. In order to determine the fractional-order extreme points of the quadratic energy norm, Y. F. Pu et al. proposed a generalization of the integer-order steepest descent method to the fractional-order one, the fractional-order steepest descent method.

Idea - Problems of image processing Just as processing one-dimensional signal, image processing should often deal with the problems of non-Gaussian, non minimum phase, non-stationary and non-linear two-dimensional signals. However, traditional approaches based on integer-order methods can not always deal with the aforementioned issues efficiently.

Idea - Inherent characteristics of fractional calculus Owing to its inherent advantages of long-term memory and non-locality. Fractional calculus can deal with the aforementioned issues, non-Gaussian, non minimum phase, non-stationary and nonlinear, efficiently. Therefore, it is one naturally to ponder how to apply fractional calculus to image processing, and how to implement fractional partial differential equations using the fractionalorder steepest descent method.

CV 1 3 Idea 2 3 Theory and applications

Theory and applications 1. Definition for fractional derivative With regard to Euclidean measurement, there are Grünwald. Letnikov, Riemann-Liouville, and Caputo definitions of fractional calculus in Euclidean space. With regard to Hausdorff measurement, we could propose Hausdorff-Besicovitch definition of fractional calculus in Hausdorff space.

Theory and applications 1. Definition for fractional calculus The commonly used fractional calculus definitions are Grünwald-Letnikov, Riemann-Liouville, and Caputo. Fractal geometry generalizes the Newton-Leibniz derivative. Fractal theory modified the perspective of measure theory; Although Hausdorff definition of fractional calculus has been studied for more than 90 years, the problems of its computability has not been well solved. In particular, Euclidean-measure-based fractional calculus is more developed than the Hausdorff-measure-based one. This is why the definition of fractional calculus based on the Euclidean measure is widely used.

Theory and applications 1. Definition for fractional calculus

Theory and applications 1. Definition for fractional calculus

Theory and applications 1. Definition for fractional calculus Therefore, it is logical to determine a mathematical induction to generalize the integer-order derivatives to the fractional-order ones (the non-integer-order, including plural, fractional and real number-order ).

Theory and applications 1. Definition for fractional calculus The Grünwald-Letnikov definition of fractional calculus for causal signal can be represented in a convenient form as follows:

Theory and applications 1. Definition for fractional calculus The Riemann-Liouville definition of the -order integral for causal signal is as follows: The Riemann-Liouville definition of the -order derivative is as follows:

Theory and applications 1. Definition for fractional calculus The Laplace transform of the -order Riemann-Liouville differential operator is as follows: When is a causal signal, and its fractional primitives must also be zero, we can simplify the above Laplace transform as follows:

Theory and applications 1. Definition for fractional calculus The Caputo definition of the -order derivative for causal signal is as follows: The Laplace transform of the -order Caputo differential operator is as follows:

Theory and applications 1. Definition for fractional calculus When is a causal signal, and its fractional primitives must also be zero, we can simplify the above Laplace transform as follows: In this case, the three cited definitions of fractional derivatives are equivalent. At this seminar, I use the equivalent notations in an interchangeable manner.

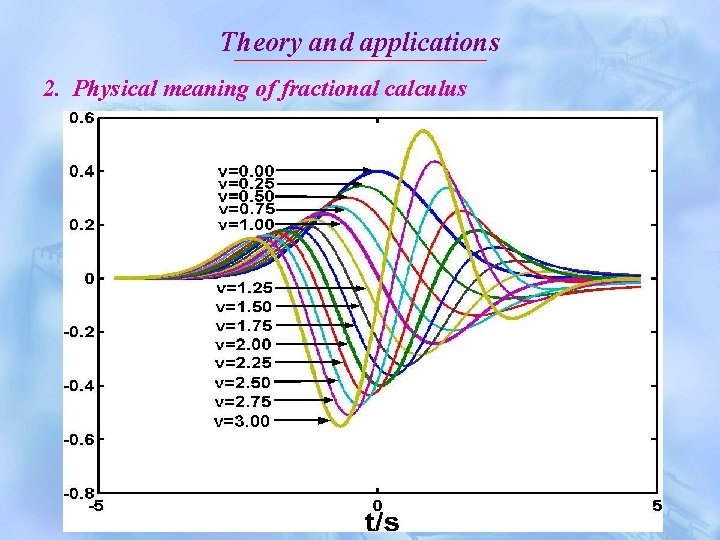
Theory and applications 2. Physical meaning of fractional calculus In the perspective of signal processing, the physical meaning of fractional calculus can be regarded as generalized amplitude-and-phase modulation. The amplitude changes with frequency as fractional power exponent, while the phase is generalized Hilbert transform of frequency.

Theory and applications 2. Physical meaning of fractional calculus Further, fractional differential is the continuous interpolation of the neighborhood order of differential.

Theory and applications 2. Physical meaning of fractional calculus

Theory and applications 2. Physical meaning of fractional calculus From above figures, we can observe that the fractional derivatives of the first-order stationary points are always non-zero. The fractional-order stationary points and the first-order stationary points are nonidentity.

Theory and applications 2. Physical meaning of fractional calculus In the perspective of dynamics, fractional derivative is a generalized derivative, note that a generalized flow or velocity. Thus, we can deduce that the physical meaning of fractional derivative is fractional flow or fractional velocity.

Theory and applications 3. The geometric meaning of fractional derivative - Fractional difference From the G-L definition of fractional calculus, we can get fractional difference as follows:

Theory and applications 3. The geometric meaning of fractional derivative - Fractional difference We can see that fractional-order difference is the common difference or generalized difference. The integer-order difference is a special case of fractional difference. The geometric meaning of fractional derivative can be seen as generalized slope of a function curve that is called fractional gradient.

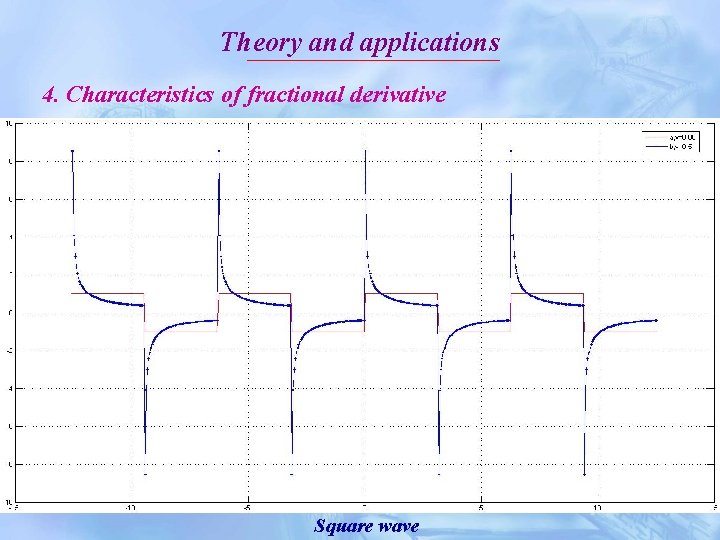
Theory and applications 4. Characteristics of fractional derivative Square wave

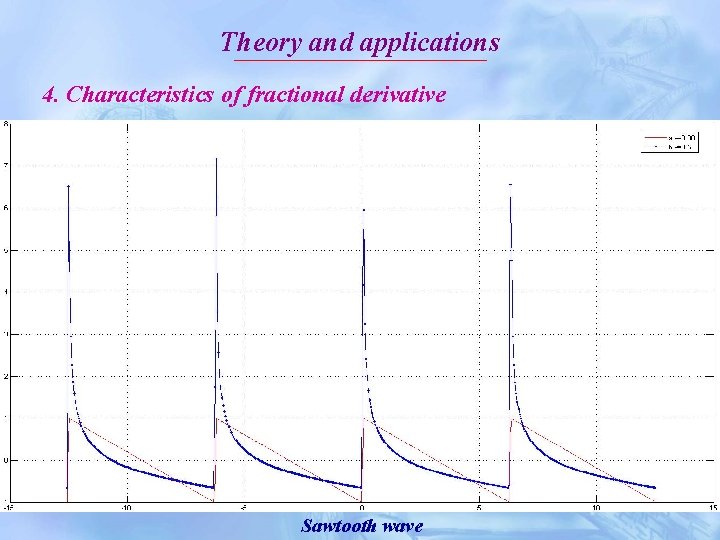
Theory and applications 4. Characteristics of fractional derivative Sawtooth wave

Theory and applications 4. Characteristics of fractional derivative In image processing, an arbitrary fractional-order derivative should include the following three properties: First, In the smooth areas, the fractional derivative of its unchanged grayscale varies from the maximum at the singular leaping point to zero gradually (non-zero). But its integer-order derivative must always be zero. This is a mainly difference between the fractional-order and integer-order derivative based approaches for image processing.

Theory and applications 4. Characteristics of fractional derivative Second, at the initial point of the slope of grayscale, its fractional derivative is non-zero. This characteristic can help us to enhance the high-frequency information of image. Third, a fractional derivative on slope section is neither zero nor a constant, but its integer-order derivative is a constant. Thus, we can use fractional derivative to nonlinearly enhance the complex texture details of image.

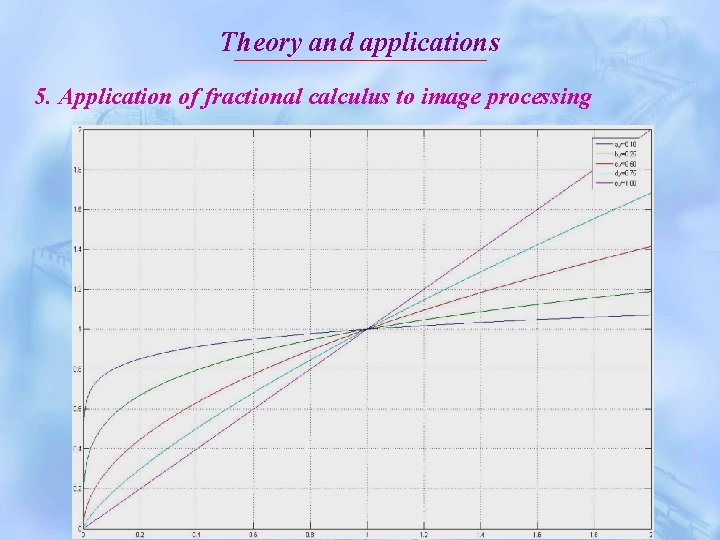
Theory and applications 5. Application of fractional calculus to image processing As aforementioned discussion, the fractional differential operator can be expressed as follows:

Theory and applications 5. Application of fractional calculus to image processing

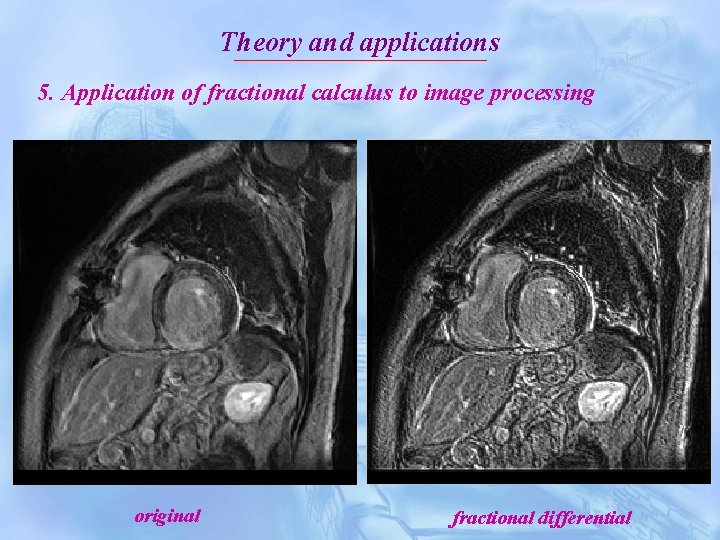
Theory and applications 5. Application of fractional calculus to image processing From above figure, we can observe some advantages of fractional differential operator as follows: - Nonlinearly preserve the low-frequency contour information. - Nonlinearly enhance the high-frequency edge information that gray scale intensively varies. - Nonlinearly enhance the high-frequency texture information in smooth areas whose grayscale does not intensively vary.

Theory and applications 2. 2 Fractional differential operator for image Suppose the duration of signal as , and then averagely divide the signal’s duration as . Thus, it has . The difference for fractional differential of one dimensional signal can be expressed as

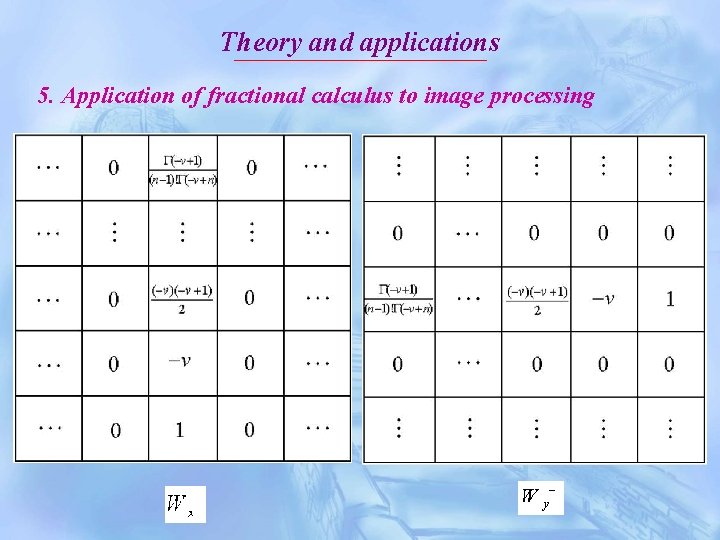
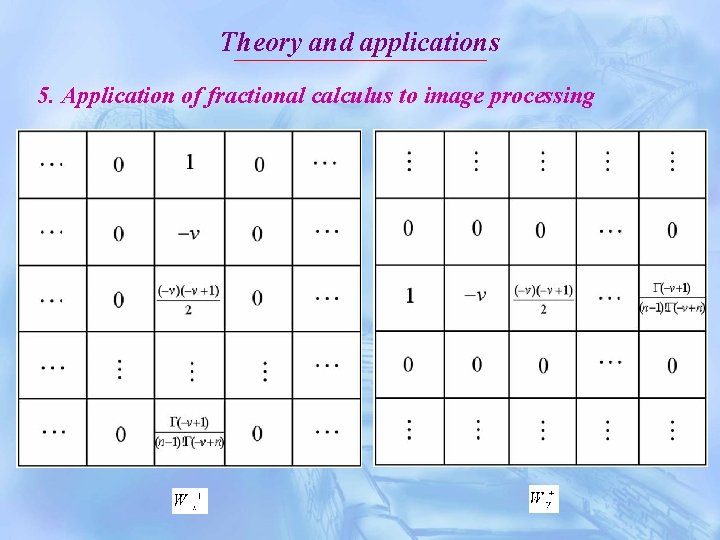
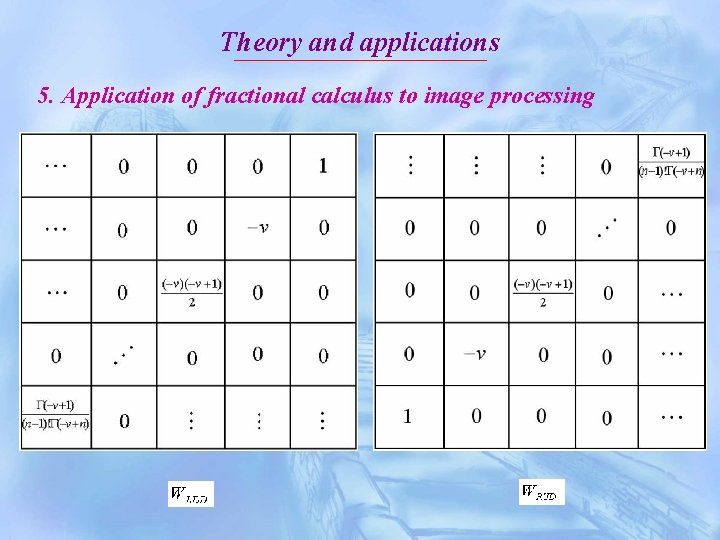
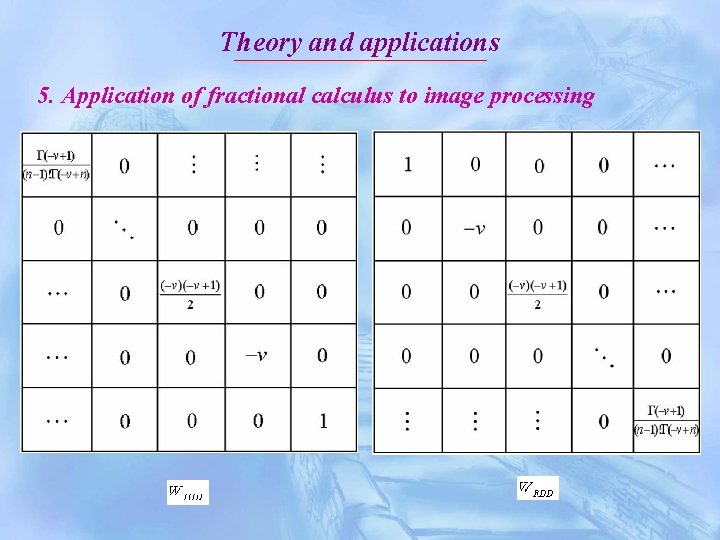
Theory and applications 5. Application of fractional calculus to image processing In order to implement the fractional differential mask of digital image, we can do partial fractional differential to two dimensional image as follows:

Theory and applications 5. Application of fractional calculus to image processing

Theory and applications 5. Application of fractional calculus to image processing

Theory and applications 5. Application of fractional calculus to image processing

Theory and applications 5. Application of fractional calculus to image processing

Theory and applications 5. Application of fractional calculus to image processing The non-zero coefficients of the fractional differential mask of image are as follows: It can be derived that the summation of the non-zero coefficients of the fractional differential mask of image is nonzero, which is a significant difference between fractional differential mask (operator) and the integer-order one.

Theory and applications 5. Application of fractional calculus to image processing original fractional differential

Theory and applications 5. Application of fractional calculus to image processing original fractional differential

Theory and applications 5. Application of fractional calculus to image processing original fractional differential

Theory and applications 5. Application of fractional calculus to image processing original fractional differential

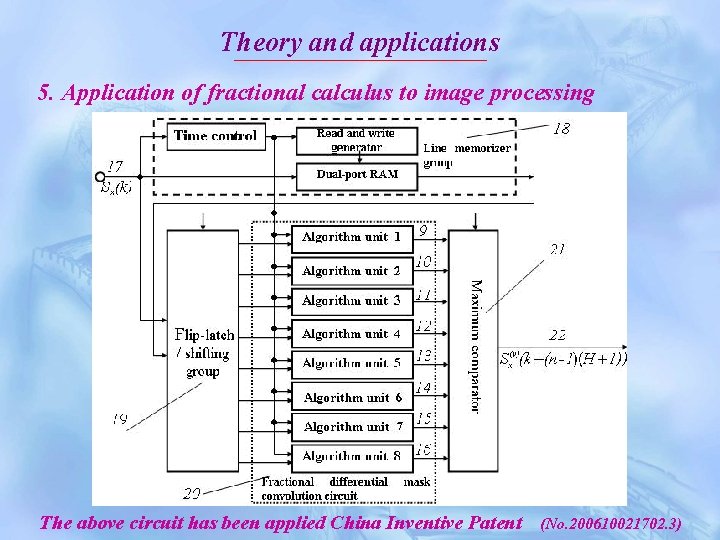
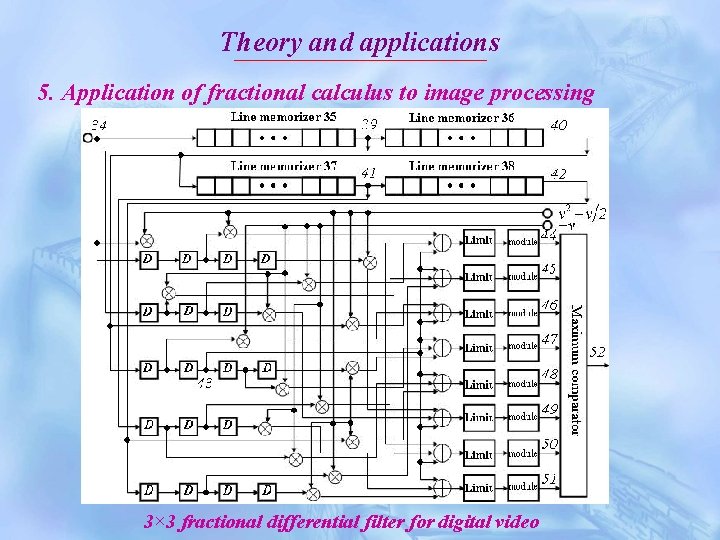
Theory and applications 5. Application of fractional calculus to image processing The above circuit has been applied China Inventive Patent (No. 200610021702. 3)

Theory and applications 5. Application of fractional calculus to image processing 3× 3 fractional differential filter for digital video

Theory and applications 6. Application of fractional partial differential equation to image processing In traditional image processing, we usually utilize arithmetic average filter, weighted average filter and mean filter to denoise and smooth image. Above-mentioned linear average filter can be expressed as follows: Where is original image, is center coordinate of neighborhood.

Theory and applications 6. Application of fractional partial differential equation to image processing Then, we can get Taylor series of at the point of (0, 0) , Maclaurin series, as follows: Where is a higher order infinitesimal.

Theory and applications 6. Application of fractional partial differential equation to image processing Not losing generality, let , then, it follows that: Where,

Theory and applications 6. Application of fractional partial differential equation to image processing Then, it follows that: If period of time is , thus, the equal division is , and .

Theory and applications 6. Application of fractional partial differential equation to image processing Then, it follows that: In a similar way, we can derive that an arbitrary linear filters of image processing accords with the heat conduction equation as follows:

Theory and applications 6. Application of fractional partial differential equation to image processing Then, it can be calculated by numerical iterative computation as follows: It is the solution of the integer-order partial differential equation, and is also the output of the linear filters of image processing.

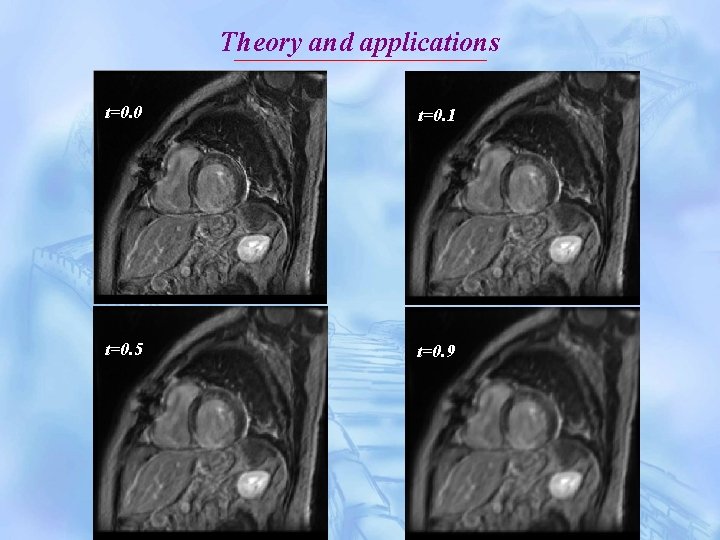
Theory and applications t=0. 0 t=0. 1 t=0. 5 t=0. 9

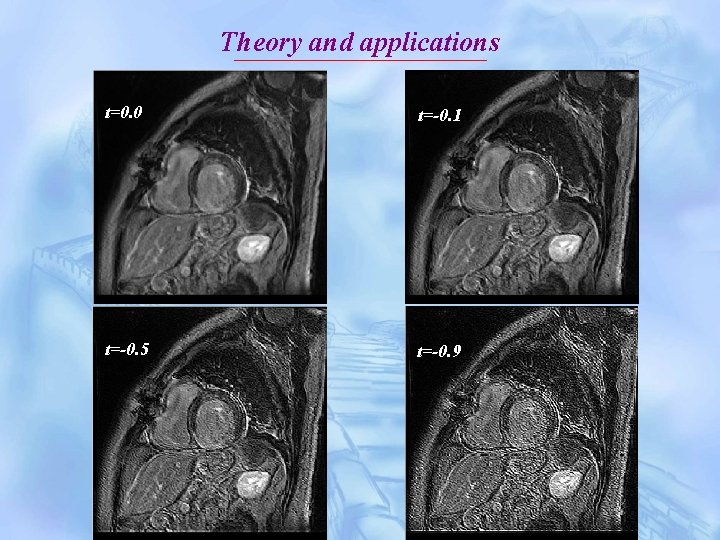
Theory and applications 6. Application of fractional partial differential equation to image processing When time t is a positive number, heat conduction equation can denoise , but it makes image blurry simultaneously. Actually, when time t increases, the denoised image becomes blurrier. So, it is logical that when time t is negative, we can get inverse integer-order partial differential equation. It could enhance the contrast of image.

Theory and applications t=0. 0 t=-0. 1 t=-0. 5 t=-0. 9

Theory and applications 6. Application of fractional partial differential equation to image processing - Wave equation - Heat conduction equation - Potential equation

Theory and applications 6. Application of fractional partial differential equation to image processing - Dilation - Erosions

Theory and applications 6. Application of fractional partial differential equation to image processing - Curvature - Mean curvature motion equation (isotropic in Euclidean space)

Theory and applications 6. Application of fractional partial differential equation to image processing Therefore, it is logical to determine a method to generalize the integer-order partial differential equations to fractional ones, and to implement fractional partial differential equations by using the fractional-order steepest descent method.

Theory and applications 6. Application of fractional partial differential equation to image processing A fractional heat conduction equation is as follows: In view of thermodynamics, above equation is fractional developmental equation. is a dissipative structure.

Theory and applications 6. Application of fractional partial differential equation to image processing Because of the time constraint, I will not present further introduction on the application of fractional partial differential equation to image processing. Some references are left as supplementary reading materials to the interested audience.

Theory and applications 7. Fractional Hopfield Networks

Theory and applications 8. Fractional Memristor

Merci beaucoup!