CS 1 Tandem Spheres Re3900 Yifei Xue and

CS 1 - Tandem Spheres Re=3900 Yifei Xue and Z. J. Wang University of Kansas Presented at HOW 5

Discretization Scheme Ø Space: FR/CPR (p 2 & p 3) § Gauss points as solution points and flux points § Roe Riemann solver § BR 2 for viscous flux Ø Time: BDF 2 optimized § Block-preconditioned LU-SGS solver § Unsteady residual reduced by 2 orders at each time step Implicit LES ØP 2 mesh generated by Grid. Pro Ø March 10, 2021 2

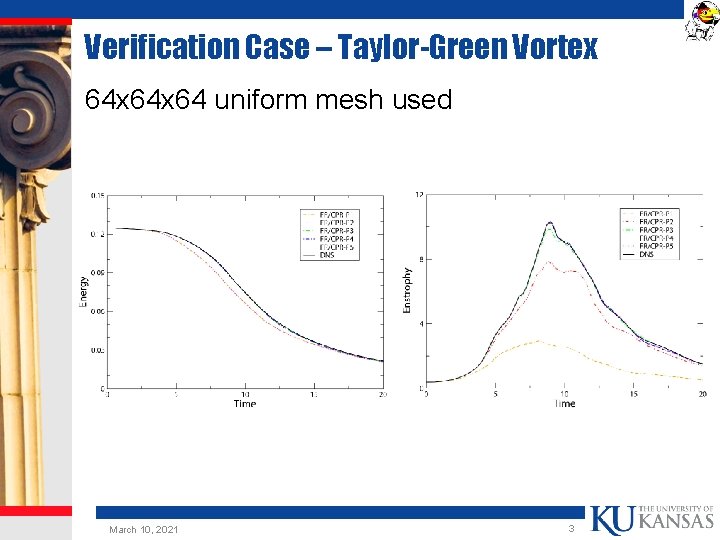
Verification Case – Taylor-Green Vortex 64 x 64 uniform mesh used March 10, 2021 3

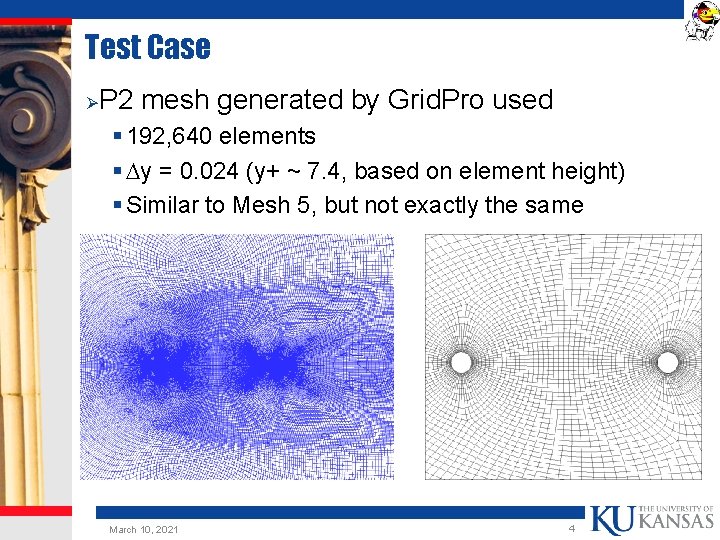
Test Case Ø P 2 mesh generated by Grid. Pro used § 192, 640 elements § Dy = 0. 024 (y+ ~ 7. 4, based on element height) § Similar to Mesh 5, but not exactly the same March 10, 2021 4

Test Case (cont. ) – Intel CPU Cluster 400 Cores Ø P 2 simulation details § n. DOFs/equ: 5. 2 M § Dt = 0. 0001 s (or 0. 0035 t*) implicit or 4. 8 e-6 s (1. 7 e-4) explicit. § Total CPU core hours: 2. 01 e 4 (explicit) and 3. 97 e 3 (implicit) § Work units: 12. 8 M and 2. 53 M Ø P 3 simulation details § n. DOFs/equ: 12. 3 M § Dt = 0. 0001 s (or 0. 0035 t*) implicit § Total CPU core hours: 1. 02 e 4 (1. 06 days wall time) § Work units: 6. 5 M Ø Tau. Bench: 5. 65 s 5

Numerical Results (P 2&P 3) Ø Ø Integral quantities – Upstream sphere: P 2 § Mean: CD = 0. 3667, CLY = -6. 412 e-04, CLZ = 1. 000 e-03 § RMS: CD = 0. 3668, CLY = 1. 234 e-2, CLZ = 1. 190 e-02 Ø P 3 § Mean: CD = 0. 3741, CLY = -6. 035 e-04, CLZ = 7. 932 e-04 § RMS: CD = 0. 3741, CLY = 4. 098 e-03, CLZ = 4. 067 e-03 March 10, 2021 6

Profiles – Center line or Sphere Surface March 10, 2021 7

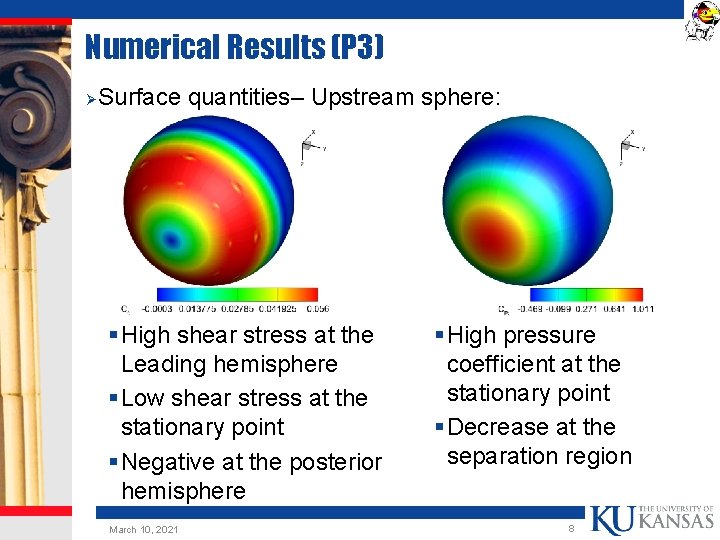
Numerical Results (P 3) Ø Surface quantities– Upstream sphere: § High shear stress at the Leading hemisphere § Low shear stress at the stationary point § Negative at the posterior hemisphere March 10, 2021 § High pressure coefficient at the stationary point § Decrease at the separation region 8

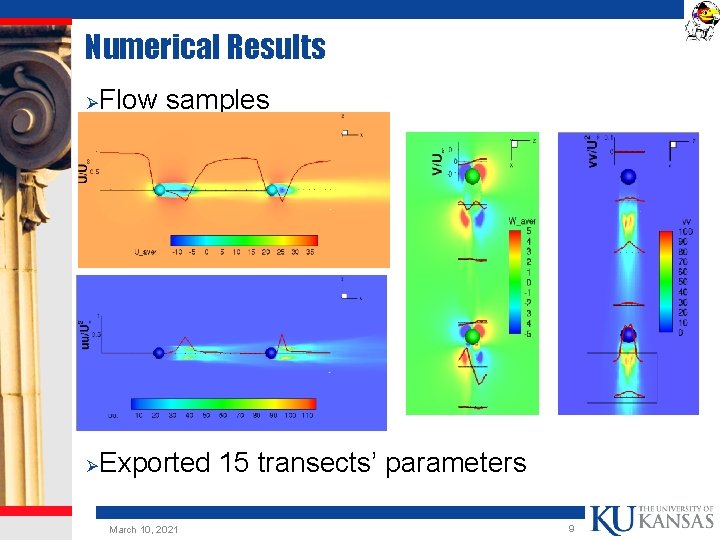
Numerical Results Ø Flow samples Ø Exported 15 transects’ parameters March 10, 2021 9

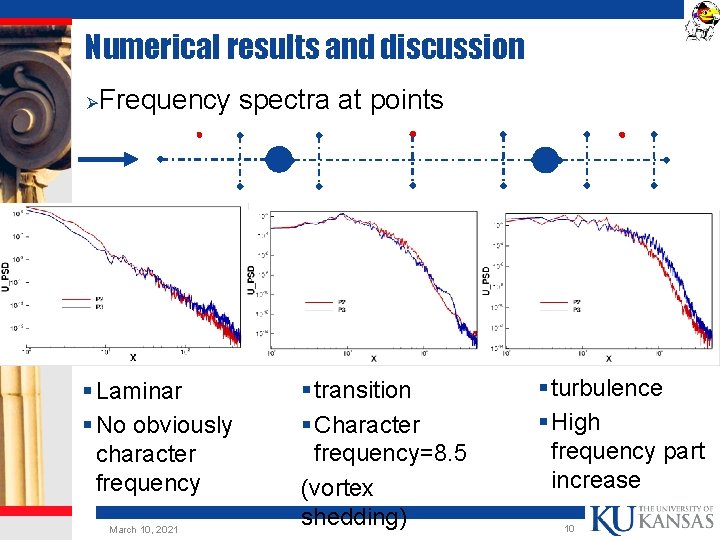
Numerical results and discussion Ø Frequency spectra at points § Laminar § No obviously character frequency March 10, 2021 § transition § Character frequency=8. 5 (vortex shedding) § turbulence § High frequency part increase 10

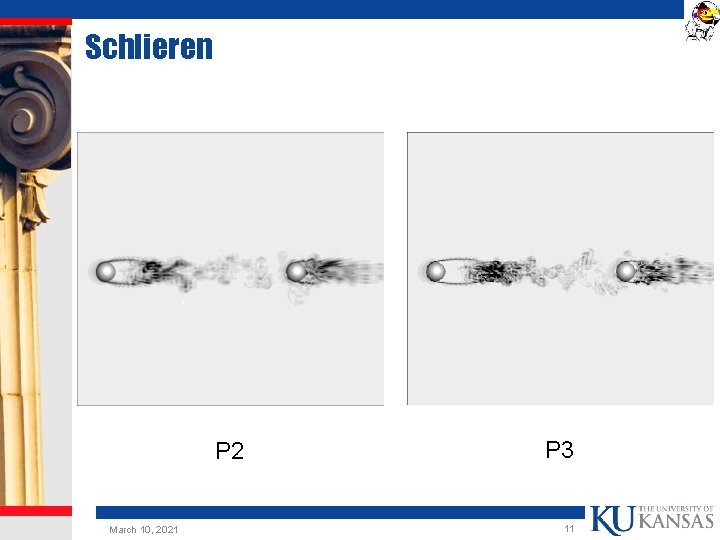
Schlieren P 2 March 10, 2021 P 3 11

Q-criterion P 2 March 10, 2021 P 3 12

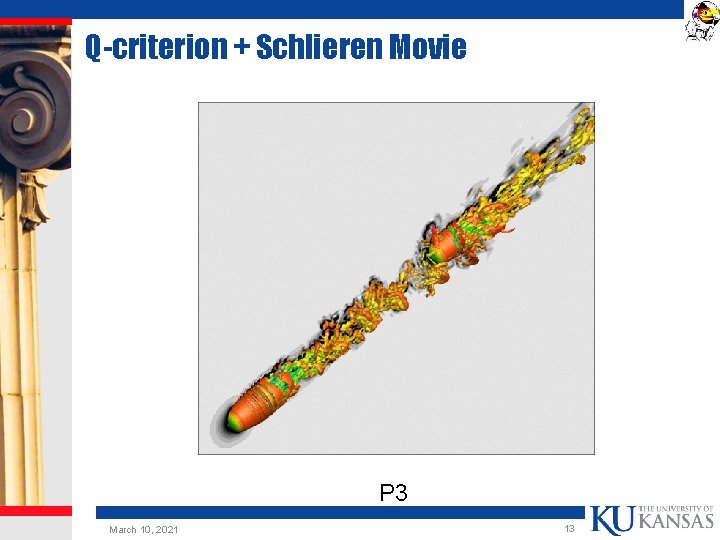
Q-criterion + Schlieren Movie P 3 March 10, 2021 13

Conclusions The verification case is useful ØToo much data asked, which may deter participation ØThe method/solver appears to handle this problem very well without any difficulty ØImplicit scheme improved efficiency by a factor of 5 Ø March 10, 2021 14

References F. Jia; J. Ims; Z. J. Wang; J. Kopriva; G. M. Laskowski, An Evaluation of a Commercial and a High Order FR/CPR Flow Solvers for Industrial Large Eddy Simulation, AIAA-2018 -0827. In Session FD-24 Ø Veer N. Vatsa, Mark H. Carpenter, David P. Lockard, Re-evaluation of an Optimized Second Order Backward Difference (BDF 2 OPT) Scheme for Unsteady Flow Applications, AIAA-2010 -0122 Ø Huynh, H. T. (2007, June). A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods. In 18 th AIAA Computational Fluid Dynamics Conference (p. 4079). Ø Z. J. Wang, Y. Li, F. Jia, G. M. Laskowski, J. Kopriva, U. Paliath, R. Bhaskaran, Towards industrial large eddy simulation using the FR/CPR method, Computers and Fluids, Volume 156, 12 October 2017, Pages 579589. Ø March 10, 2021 15