y para Continuacin demostracin 0 cte q e

y, para

Continuación demostración 0 cte q. e. d.

Cálculo y demostraciones relativas a la “derivada direccional”, se facilitan introduciendo el concepto de “vector gradiente” , ) ( Teo 3 ( versor de dirección) = CONCLUSIÓN: = ( : versor de dirección ) y x

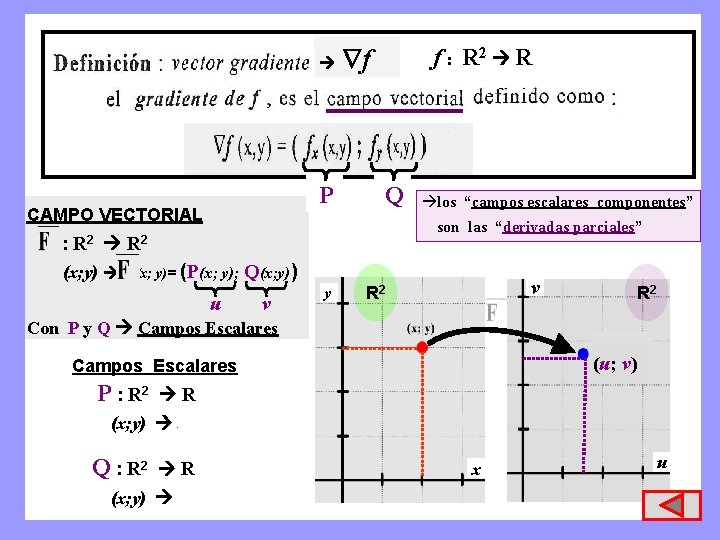
P CAMPO VECTORIAL f f : R 2 R Q son las “derivadas parciales” : R 2 (x; y)= àlos “campos escalares componentes” (P(x; y); Q(x; y)) u v y v R 2 Con P y Q Campos Escalares (u; v) Campos Escalares P : R 2 R (x; y) u = P(x; y) Q : R 2 R (x; y) v = Q(x; y) x u

RESUMEN: y x

b)

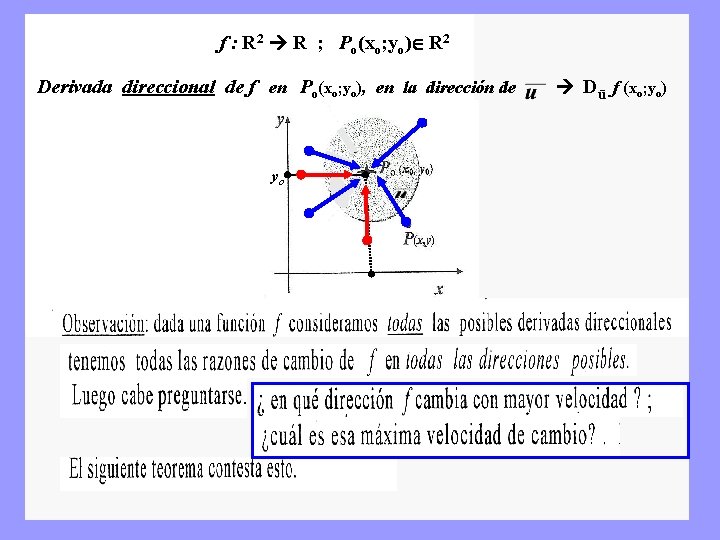
f : R 2 R ; Po(xo; yo) R 2 Derivada direccional de f en Po(xo; yo), en la dirección de yo xo Dū f (xo; yo)

es es

e igual a: (40; 30) = a partir de (40; 30) y en la dirección del gradiente la temperatura aumenta, aprox. , a razón de 0. 34 ºC por unidad de distancia

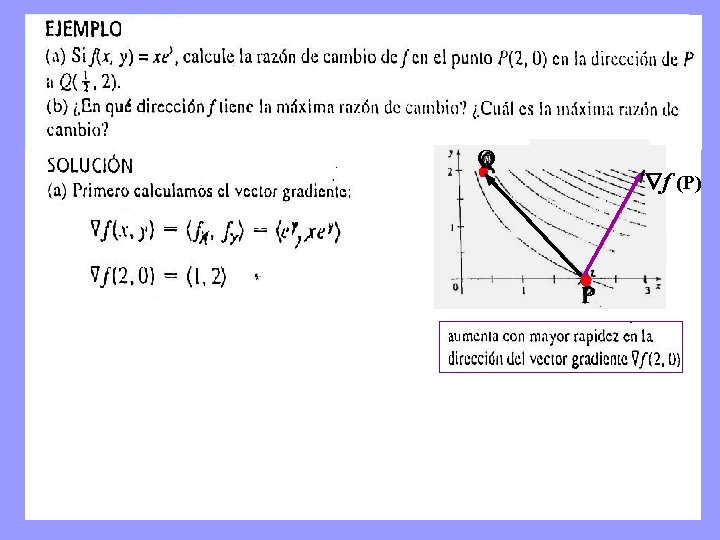
Q f (P) P

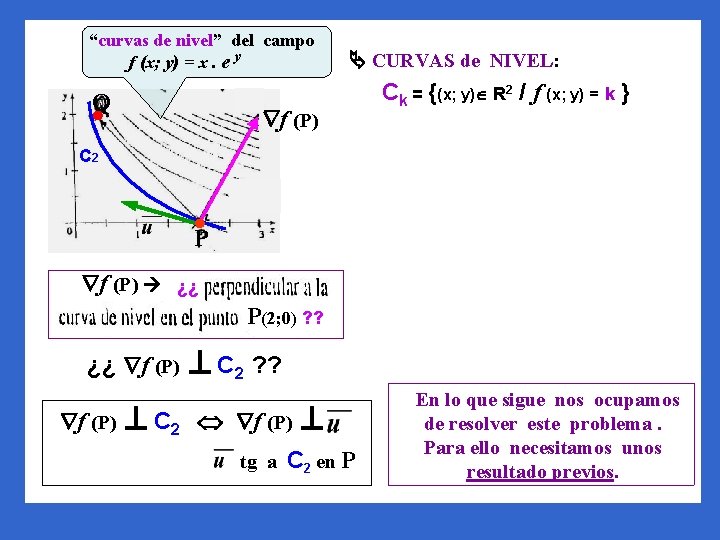
“curvas de nivel” del campo f (x; y) = x. e y Q Ck = {(x; y) R 2 / f (x; y) = k } Ck = {(x; y) R 2 / x. e y = k } f (P) C 2 curvas de nivel P f (P) ¿¿ P(2; 0) ? ? ¿¿ f (P) CURVAS de NIVEL: C 2 para k >0 y x > 0 Ck = { (x; y) R 2 / y = - ln x + ln k } para k = 2 C 2 = { (x; y) R 2 / y = - ln x + ln 2 } P(2; 0) C 2 ? ? f (P) tg a C 2 en P En lo que sigue nos ocupamos de resolver este problema. Para ello necesitamos unos resultado previos.

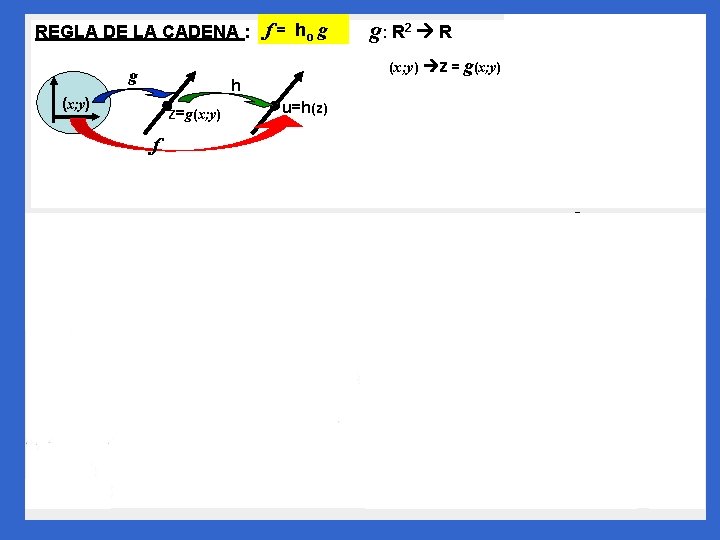
REGLA DE LA CADENA : f = ho g g Z=g(x; y) ; h: R R (x; y) z = g(x; y) h (x; y) g: R 2 R u=h(z) z u=h(z) f (x; y) = ho g (x; y) f : R 2 R (x; y) u = ho g (x; y) f h´(g(x; y)). u= h(z) = sen z g(x; y) = u= hog (x; y)

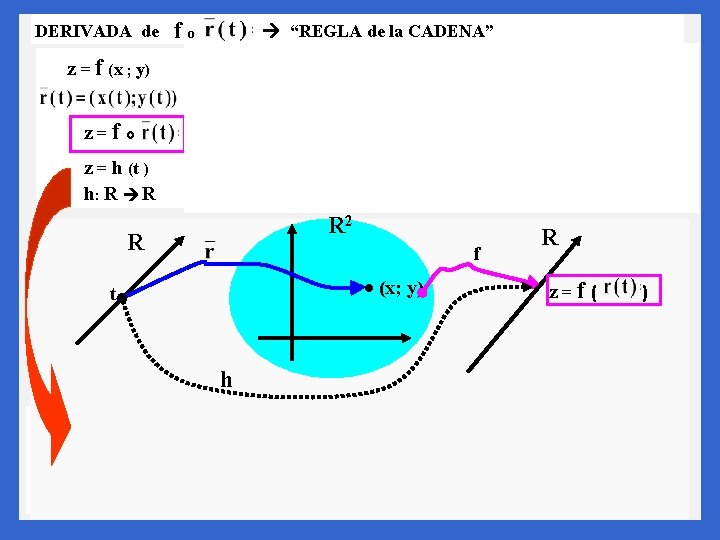
DERIVADA de fo “REGLA de la CADENA” z = f (x ; y) z=f x = x(t) ; y = y(t) t Existen otras formas de “escribir” la “regla de la cadena” , formas que “facilitan” el hecho de recordarla. o z = h (t ) h: R R R 2 R f (x; y) t h z´(to) = + R zz = f ( )

Si T = f (x ; y) ; ecuación vectorial de una curva C T=f o T T = f (x; y) = 100 – x 2 – 4 y 2. Un “alienígena” inicialmente parado en la plancha en el punto A(5; 0) comienza a moverse sobre la misma según la curva C de ecuación: t; 0); t 0 (t Se pide: a) Hallar T = f b) Calcular o 5) ; (5) ; T=f o (0) en minutos) 0) interpretar físicamente el resultado.

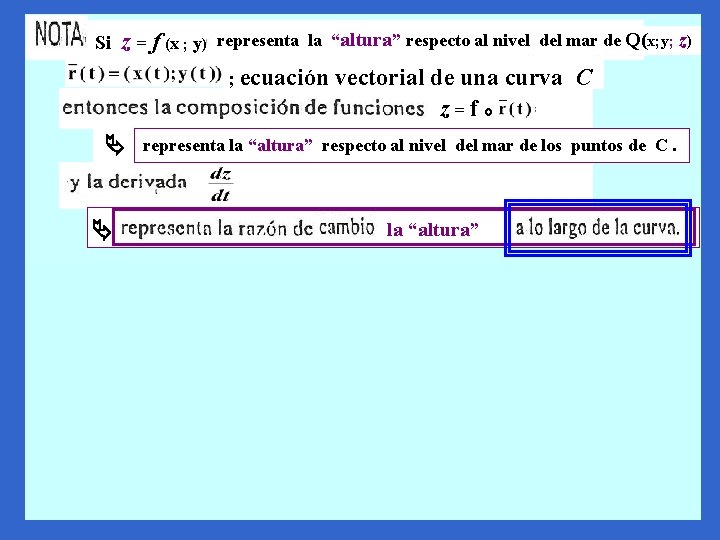
Si z = f (x ; y) representa la “altura” respecto al nivel del mar de Q(x; y; z) ; ecuación vectorial de una curva C z=f o representa la “altura” respecto al nivel del mar de los puntos de C. la “altura” si z = f (x; y) = 100 – x 2 – 4 y 2 describe una “montaña” entonces “z” da la “altura” respecto al nivel del mar de los puntos de la montaña. Un “turista” que sobre la montaña está a 84 mts del nivel del mar, encuentra un senderos que decide recorrer. Si la ecuación que (sobre la base de la montaña) describe el sendero C, es (4 cos t, 2 sen t ) ; t 0 (t en minutos) Se pide: a) Hallar z = f b) Calcular o 0) ; (0 ) ; z=f o (t) t) interpretar físicamente el resultado.

Q ¿¿ f (P) C 2 ? ? Habíamos dejado en suspenso la resolución de este problema pues nos faltaban herramientas teóricas para analizarlo. “curvas de nivel” del campo f (x; y) = x. e y f (P) C 2 curvas de nivel P f (P) C 2 f (P) tg a C 2 en P Tenemos ya las herramientas, (sabemos derivar composición de campo escalar con función vectorial) entonces…. manos a la obra.

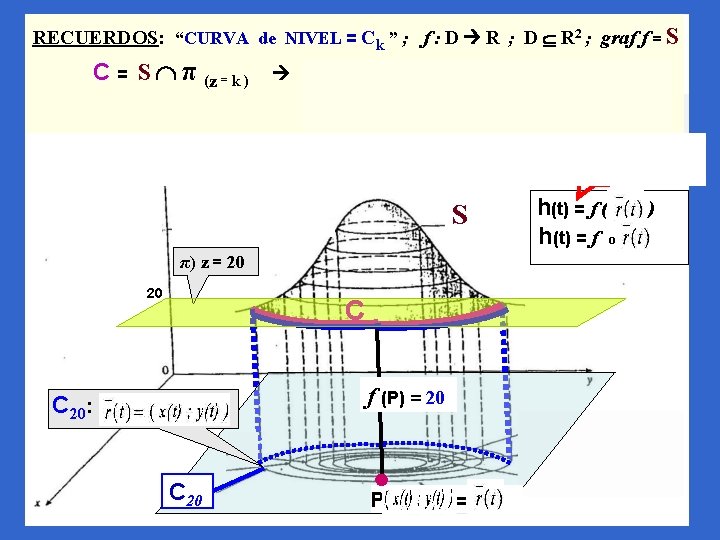
RECUERDOS: “CURVA de NIVEL = Ck ” ; f : D R ; D R 2 ; graf f = S C = S π (z = k ) C 20 = { P( x; y ) / Ck = “proyección” sobre πx y de C Ck = { P(x; y) D / f (x ; y) = k } πx y f ( x; y )= 20 } C 20 = { P( S π) z = 20 20 C f (P) = 20 C 20: C 20 PP (x; y) = )/ f ( h(t) = f o ) = 20 } )

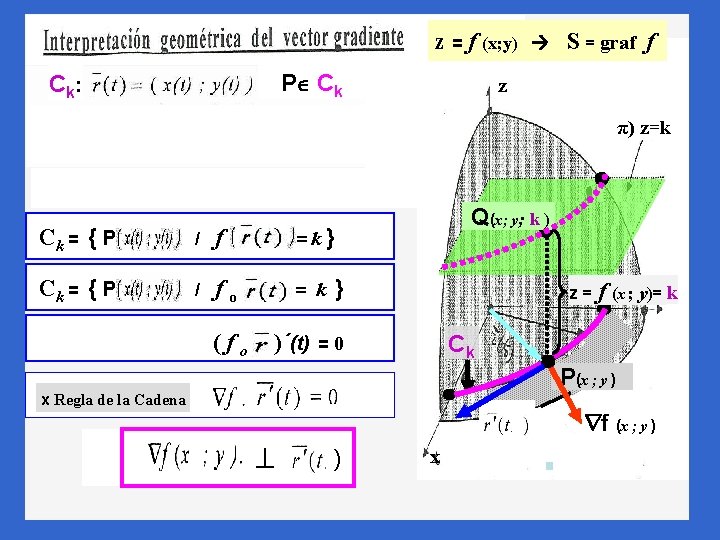
z = f (x; y) P Ck C k: S = graf f z π) z=k = OP P Ck Ck = { P / f =k} Ck = { P / fo = k (fo )´(t) Q(x; y; k ) } z = f (x ; y)= k Ck =0 P(x ; y ) x Regla de la Cadena f (x ; y ) ) x

: z = k Q(x ; y ; k) Ck Ck curva de nivel que pasa por P(x; y) f (x ; y ) Ck P (x; y) r´ (t) f (x ; y ) finalmente tenemos que: “en P , el crecimiento más rápido de la función se da en una dirección perpendicular a la curva de nivel que pasa por P ”.

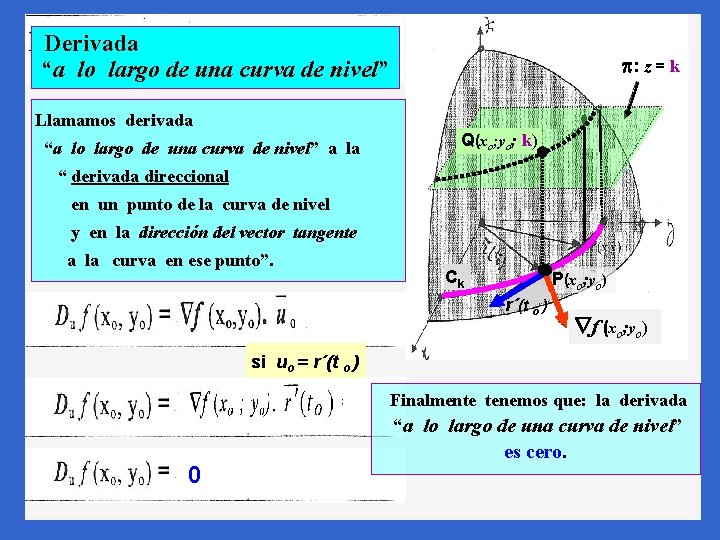
Derivada “a lo largo de una curva de nivel” : z = k . Llamamos derivada “a lo largo de una curva de nivel” a la Q(xo; yo; k) “ derivada direccional en un punto de la curva de nivel y en la dirección del vector tangente a la curva en ese punto”. Ck P(xo; yo) r´(t o ) f (xo; yo) si uo = r´(t o ) Finalmente tenemos que: la derivada 0 “a lo largo de una curva de nivel” es cero.