Video Game Math CircleonCircle collision detection Sample Game

Video Game Math: Circle-on-Circle collision detection

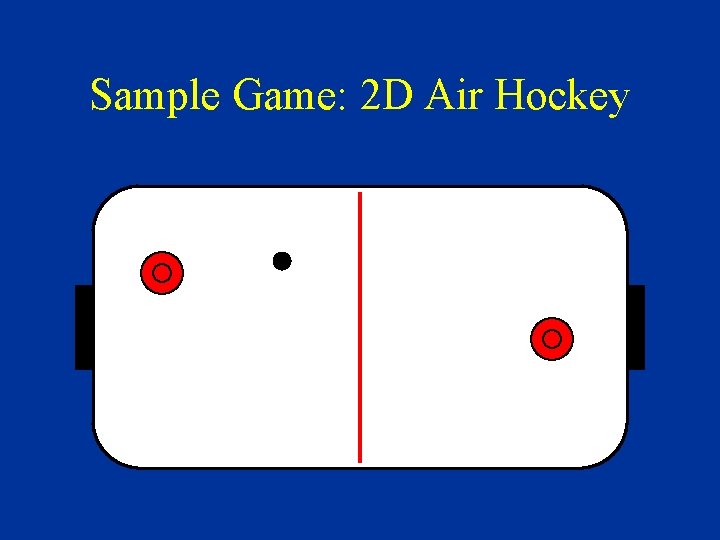
Sample Game: 2 D Air Hockey

Like a movie, the action of a video game happens in frames.

Like a movie, the action of a video game happens in frames.

Like a movie, the action of a video game happens in frames.

Like a movie, the action of a video game happens in frames.

The math problem: • In a given frame, how do we tell when the puck hits the paddle?

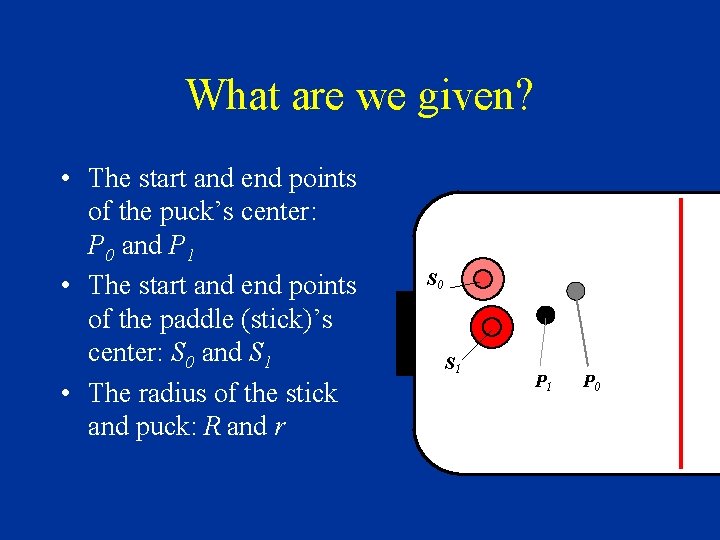
What are we given? • The start and end points of the puck’s center: P 0 and P 1 • The start and end points of the paddle (stick)’s center: S 0 and S 1 • The radius of the stick and puck: R and r S 0 S 1 P 0

Points are Coordinate Pairs • Each of the four points we are given is expressed as an (x, y) pair. In other words: P 0 = (P 0 x, P 0 y)

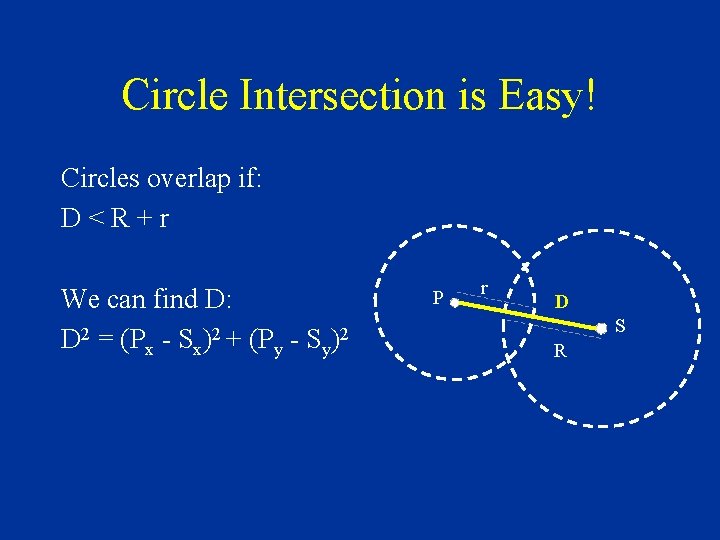
Circle Intersection is Easy! Circles overlap if: D<R+r We can find D: D 2 = (Px - Sx)2 + (Py - Sy)2 P r D S R

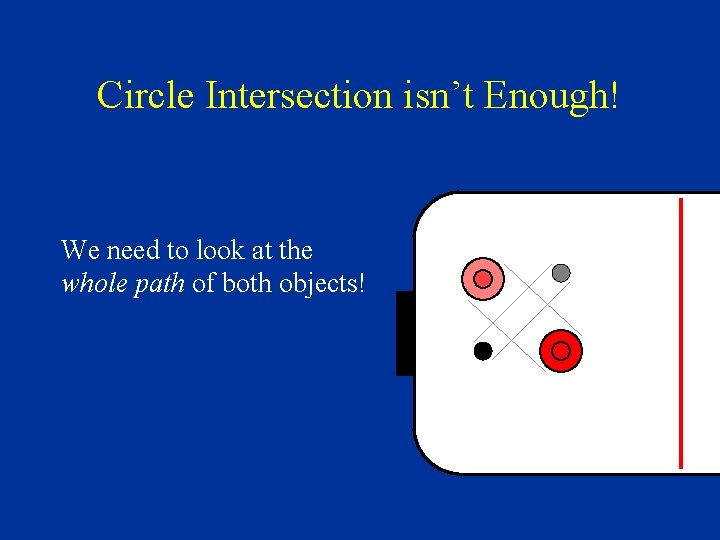
Circle Intersection isn’t Enough! We need to look at the whole path of both objects!

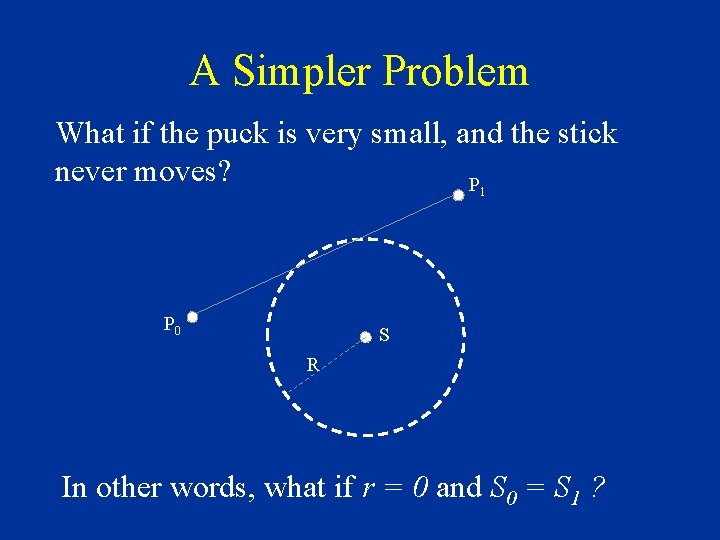
A Simpler Problem What if the puck is very small, and the stick never moves? P 1 P 0 S R In other words, what if r = 0 and S 0 = S 1 ?

Definitions & Constructions Let L = length of P 0 P 1 Lx = P 1 x - P 0 x Ly = P 1 y - P 0 y L 2= Lx 2 + Ly 2 P 1 L P 0 S R

Definitions & Constructions Let C = length of P 0 S Cx = Sx - P 0 x Cy = Sy - P 0 y C 2= Cx 2 + Cy 2 P 1 L P 0 S C R

Definitions & Constructions Let Θ = angle P 2 P 1 S P 1 L P 0 Θ C S R

Definitions & Constructions Let Θ = angle P 2 P 1 S We weren’t given Θ! We’ll solve for it later. P 1 L P 0 Θ C S R

Equation for Line P 0 P 1 Introduce parameter t P 1 Px(t) = P 0 x + t(P 1 x - P 0 x) Py(t) = P 0 y + t(P 1 y - P 0 y) P(t) P 0 L Θ C S R P(t) is the point ( Px(t), Px(t) )

Equation for Line P 0 P 1 Introduce parameter t P 1 Px(t) = P 0 x + t. Lx Py(t) = P 0 y + t. Ly P(t) P 0 L Θ C S R P(t) is the point ( Px(t), Px(t) )

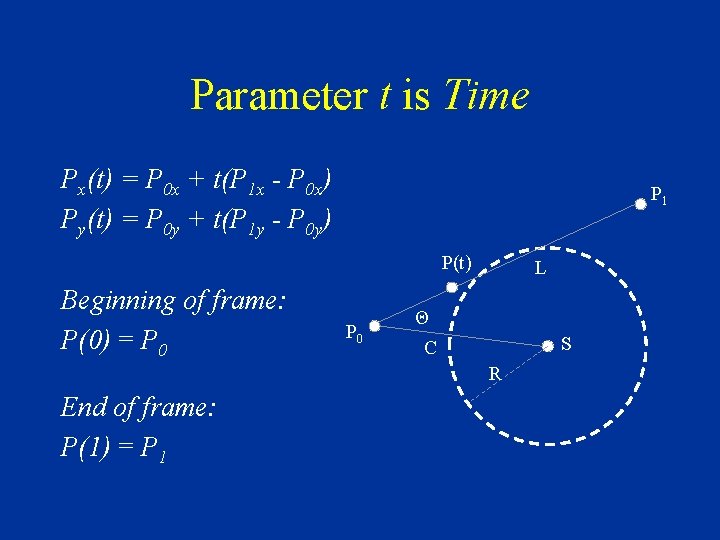
Parameter t is Time Px(t) = P 0 x + t(P 1 x - P 0 x) Py(t) = P 0 y + t(P 1 y - P 0 y) P 1 P(t) Beginning of frame: P(0) = P 0 L Θ C S R End of frame: P(1) = P 1

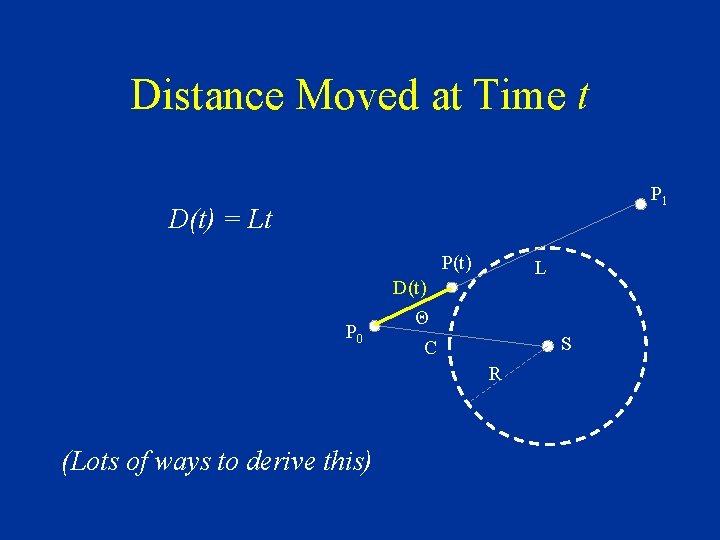
Distance Moved at Time t P 1 D(t) = Lt P(t) L D(t) P 0 Θ C S R (Lots of ways to derive this)

We’re Finally Ready to Solve! Suppose P(t) is the point of impact. P 1 P(t) Solve for t, the time of impact. Lt P 0 Θ C L R S

Using the Law of Cosines R 2 = (Lt)2 + C 2 - 2 CLt cos Θ 0 = L 2 t 2 - 2 t. CL cos Θ + C 2 - R 2 P 0 P 1 P(t) Lt Θ C L R S

One more definition So far we have: L 2 t 2 - 2 t. CL cos Θ + C 2 - R 2 = 0 P 1 P(t) Lt Let α = CL cos Θ P 0 now: L 2 t 2 - 2αt + C 2 - R 2 = 0 Θ C L R S

Applying the Quadratic Formula So far we have: L 2 t 2 - 2αt + C 2 - R 2 = 0 P 1 P(t) Lt So: P 0 Θ C L R S

Examining the Discriminant = α 2 - L 2(C 2 - R 2)

Examining the Discriminant = α 2 - L 2(C 2 - R 2) If Discriminant < 0, no solutions P 1 P 0 S

Examining the Discriminant = α 2 - L 2(C 2 - R 2) If Discriminant < 0, no solutions If Discriminant > 0, two solutions P 1 P 0 S We want the earlier solution.

Examining the Discriminant = α 2 - L 2(C 2 - R 2) If Discriminant < 0, no solutions If Discriminant > 0, two solutions If Discriminant = 0, one solution We want the earlier solution. P 1 P 0 S

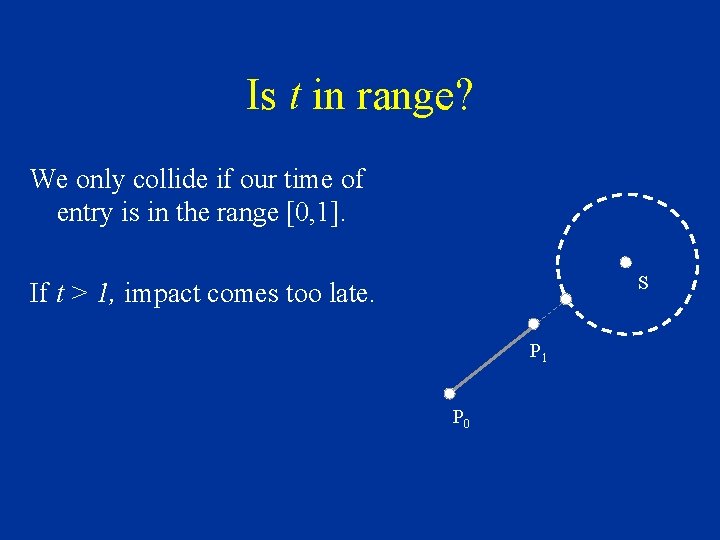
Is t in range? We only collide if our time of entry is in the range [0, 1]. S If t > 1, impact comes too late. P 1 P 0

Is t in range? We only collide if our time of entry is in the range [0, 1]. If t > 1, impact comes too late. If t < 0, impact is in the past. P 1 P 0 S

Is t in range? We only collide if our time of entry is in the range [0, 1]. P 1 If t > 1, impact comes too late. If t < 0, impact is in the past. . Or maybe we started intersecting. S P 0

We still need to solve for Θ! Remember, α = CL cos Θ P 1 We construct K L P 0 By the law of cosines, K 2 = L 2 + C 2 - 2 CL cos Θ That is: K 2 = L 2 + C 2 - 2α Θ C K S

We only need to solve for α. We have: K 2 = L 2 + C 2 - 2α P 1 We also know: K 2 = (P 2 x - Sx)2 + (P 2 y - Sy)2 L P 0 K Θ C S

We only need to solve for α. We have: K 2 = L 2 + C 2 - 2α P 1 We also know: K 2 = (P 2 x - Sx)2 + (P 2 y - Sy)2 L P 0 We can also show: P 2 x - Sx = Lx - Cx P 2 y - Sy = Ly - Cy K Θ C S

Then, a bunch of algebra happens. . . K 2 = (Lx - Cx)2 + (Ly - Cy)2 P 1 L P 0 K Θ C S

Then, a bunch of algebra happens. . . K 2 = (Lx - Cx)2 + (Ly - Cy)2 P 1 = L x 2 + C x 2 + L y 2 - C y 2 - 2 Lx. Cx - 2 Ly. Cy L P 0 K Θ C S

Then, a bunch of algebra happens. . . K 2 = (Lx - Cx)2 + (Ly - Cy)2 P 1 = L x 2 + C x 2 + L y 2 - C y 2 - 2 Lx. Cx - 2 Ly. Cy L P 0 = L x 2 + L y 2 + C x 2 + C y 2 - 2 Lx. Cx - 2 Ly. Cy K Θ C S

Then, a bunch of algebra happens. . . K 2 = (Lx - Cx)2 + (Ly - Cy)2 P 1 = L x 2 + C x 2 + L y 2 - C y 2 - 2 Lx. Cx - 2 Ly. Cy L P 0 = L x 2 + L y 2 + C x 2 + C y 2 - 2 Lx. Cx - 2 Ly. Cy K 2 = L 2 + C 2 - 2 Lx. Cx - 2 Ly. Cy K Θ C S

Then, a bunch of algebra happens. . . We have: K 2 = L 2 + C 2 - 2 Lx. Cx - 2 Ly. Cy K 2 = L 2 + C 2 - 2α P 0 2α = 2 Lx. Cx + 2 Ly. Cy α = L x. C x + L y. C y P 1 L K Θ C S

Then, a bunch of algebra happens. . . We have: K 2 = L 2 + C 2 - 2 Lx. Cx - 2 Ly. Cy K 2 = L 2 + C 2 - 2α P 0 2α = 2 Lx. Cx + 2 Ly. Cy α = L x. C x + L y. C y Ax. Bx + Ay. By = AB cos Θ P 1 L K Θ C S

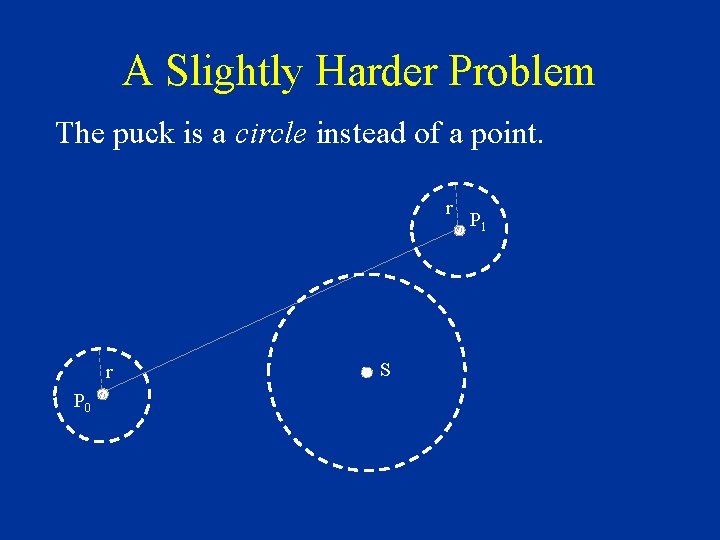
A Slightly Harder Problem The puck is a circle instead of a point. r r P 0 S P 1

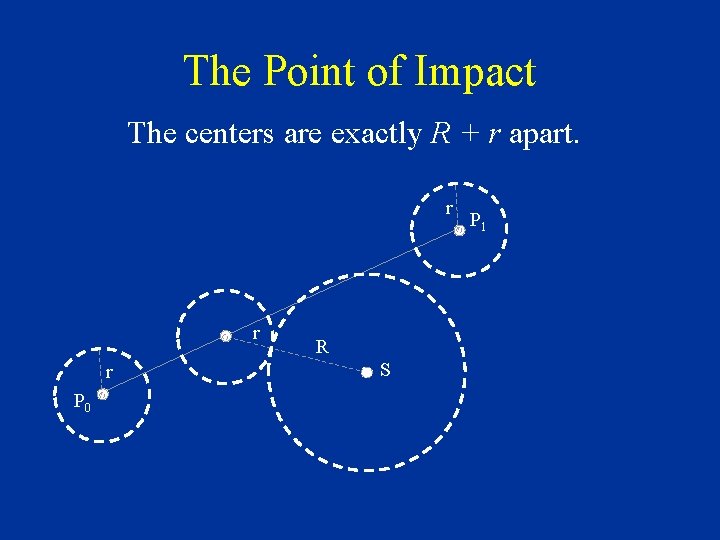
The Point of Impact The centers are exactly R + r apart. r r r P 0 R S P 1

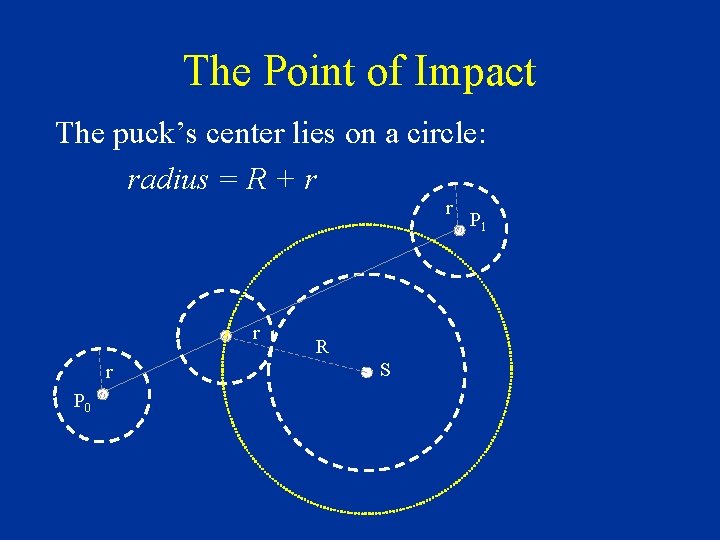
The Point of Impact The puck’s center lies on a circle: radius = R + r r P 0 R S P 1

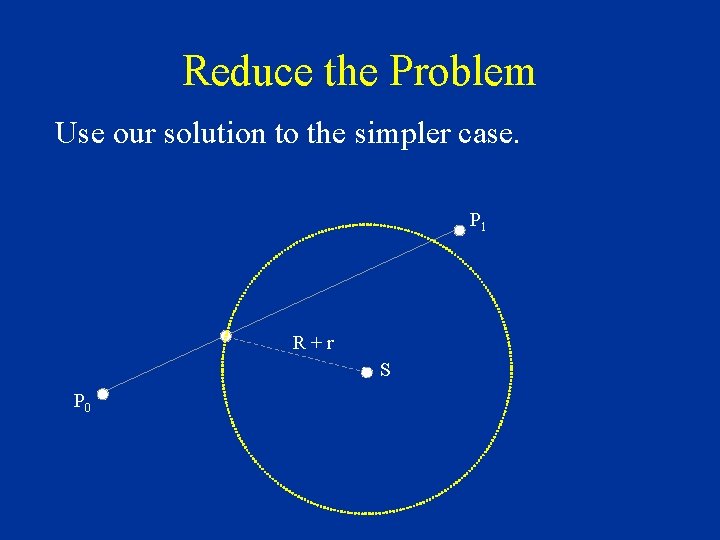
Reduce the Problem Use our solution to the simpler case. P 1 R+r S P 0

The Original Problem Two Moving Circles S 1 R r r P 0 R S 0 P 1

Change our Frame of Reference Just Imagine that the stick is stationary. r r P 0 R S 0 P 1

Change our Frame of Reference Consider the relative motion of the puck. r P 0 R S 0 r P 1

Once Again, Reduce the Problem Use our earlier solution. r P 0 R S 0 r P 1

Let’s See That Again. . . How exactly do we find the relative motion? R P 0 S 1 r P 1 r R S 0

Let’s See That Again. . . We need to subtract the motion of S from the motion of P. P 2 x = P 1 x - (S 1 x - S 0 x) P 2 y = P 1 y - (S 1 y - S 0 y) S 1 P 0 r P 1 S 0 R P 2

Now you can make an Air Hockey Game! (well, not quite)

Other Problems to Solve • Collision detection for puck vs walls. • What happens as a result of the collisions. • All that pesky programming stuff.

The 3 D Problem The math is the same, except: • Points are (x, y, z) triples. • The objects are spheres, not circles. • L 2= Lx 2 + Ly 2 + Lz 2 • α = L x C x + L y C y + L z. C z

Questions?