Physics for Games Programmers Continuous Collision Detection Gino

Physics for Games Programmers: Continuous Collision Detection Gino van den Bergen > Playlogic Game Factory > gino@dtecta. co m >

Overview Discuss the GJK algorithm and show to tailor it for detecting space-time collisions. > Discuss the Sweep and Prune algorithm and show to tailor it for doing a broad phase in space-time. >

Space-time Collision Detection > Perform collision detection in continuous space-time: Construct a plausible trajectory for each moving object. > Detect collisions along these trajectories, using time as an added dimension. > Obtain expected time of impact and contact data for colliding pairs. >

Plausible Trajectory? Limited to trajectories with piecewise constant linear velocities. > Angular velocities are ignored. Rotations are considered instantaneous. >

Only Translations Solving continuous rotations is a lot more complex, so we’d rather dodge the issue. > Tunneling may occur for rotating objects, but is less visible and often acceptable. > Doing continuous translations only already fixes most of our problems and is doable in real time. >

GJK Algorithm: Overview An iterative method for computing the distance between convex objects. > First publication in 1988 by Gilbert, Johnson, and Keerthi. > Solves queries in configuration space. > Uses an implicit object representation. >

GJK Algorithm: Pros > Extremely versatile: Applicable to any combination of convex shape types. > Computes distances, common points, and separating axes. > Can be tailored for finding space-time collisions. > Allows a smooth trade-off between accuracy and speed. >

GJK Algorithm: Pros (cont'd) > Performs well: Exploits frame coherence. > Competitive with dedicated solutions for polytopes (Lin-Canny, V-Clip, SWIFT). > Despite its conceptual complexity, implementing GJK is not too difficult. > Small code size. >

GJK Algorithm: Cons > Difficult to grasp: Concepts from linear algebra and convex analysis (determinants, Minkowski addition), take some time to get comfortable with. > Maintaining a “geometric” mental image of the workings of the algorithm is challenging and not very helpful. >

GJK Algorithm: Cons (cont'd) > Suffers from numerical issues: Termination is governed by predicates that rely on tolerances. > Despite the use of tolerances, certain “hacks” are needed in order to guarantee termination in all cases. > Using 32 -bit floating-point numbers is doable but tricky. >

Configuration Space (recap) > A and B intersect: A – B contains origin. > Distance between A and B: length of shortest vector in A – B.

GJK Algorithm: Workings > Approximate the point of the CSO closest to the origin: Generate a sequence of simplices inside the CSO, each simplex lying closer to the origin than its predecessor. > Terminate as soon as the current simplex is close enough. > In case of an intersection, the simplex contains the origin. >

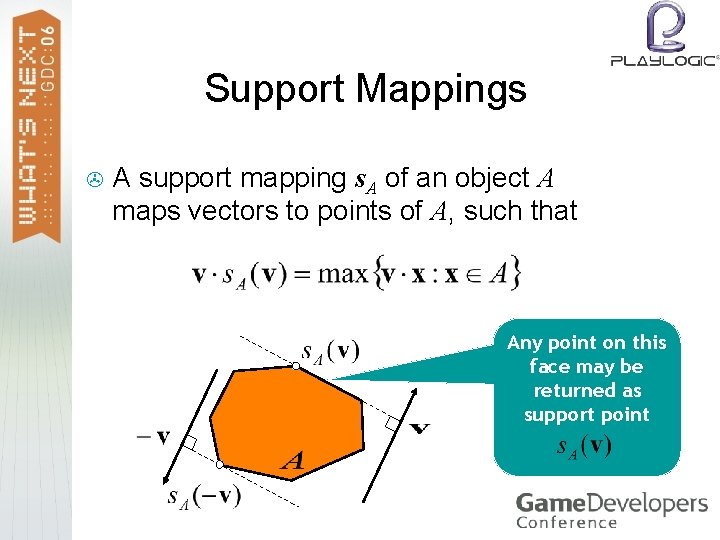
Support Mappings > A support mapping s. A of an object A maps vectors to points of A, such that Any point on this face may be returned as support point

Primitives

More Primitives

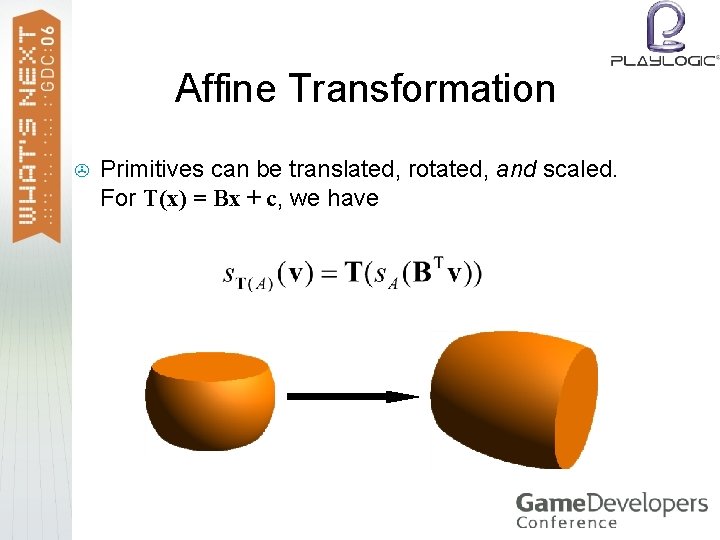
Affine Transformation > Primitives can be translated, rotated, and scaled. For T(x) = Bx + c, we have

Convex Hull > Convex hulls of arbitrary convex shapes are readily available.

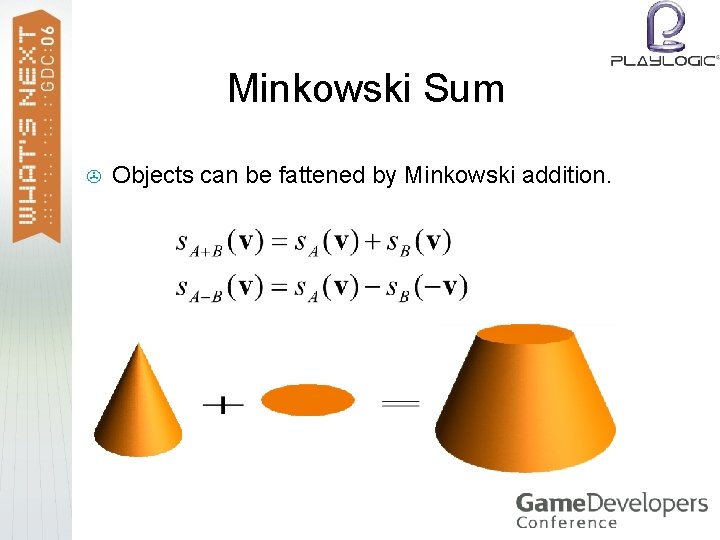
Minkowski Sum > Objects can be fattened by Minkowski addition.

Basic Steps (1/6) > Suppose we have a simplex inside the CSO…

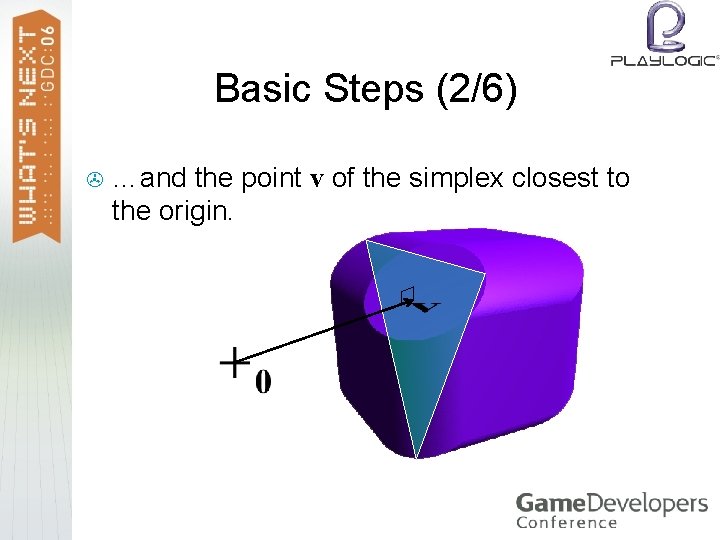
Basic Steps (2/6) > …and the point v of the simplex closest to the origin.

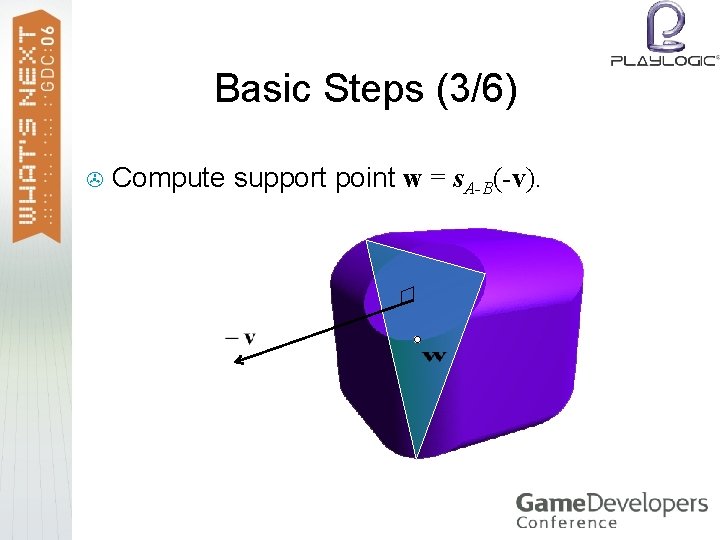
Basic Steps (3/6) > Compute support point w = s. A-B(-v).

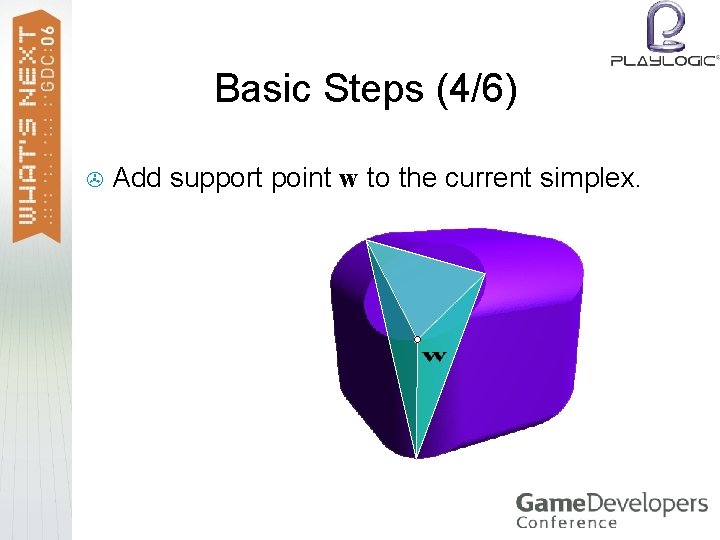
Basic Steps (4/6) > Add support point w to the current simplex.

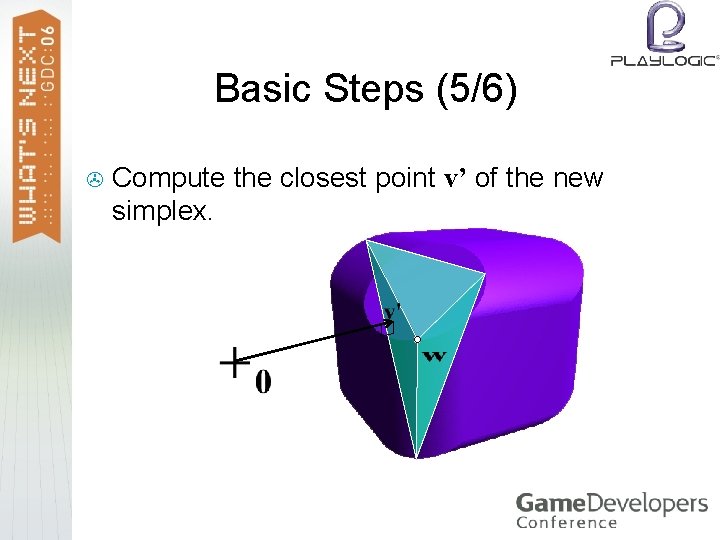
Basic Steps (5/6) > Compute the closest point v’ of the new simplex.

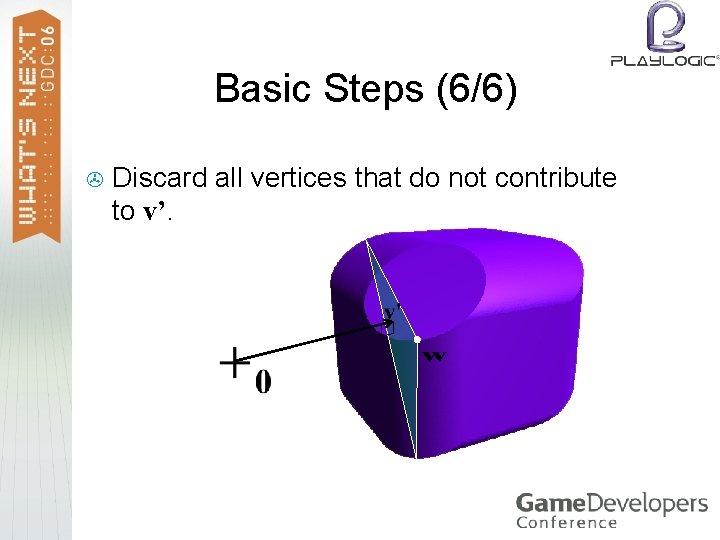
Basic Steps (6/6) > Discard all vertices that do not contribute to v’.

Affine Hull > The affine hull of points yi is the set of points x for which > The parameters λi are better known as barycentric coordinates of x with respect to yi. Point set Y is affinely independent if no y in Y is contained in the affine hull of Y {y}. >

Closest Point of a Simplex > The point closest to the origin of a simplex: Lies in the affine hull of the simplex. > Has non-negative barycentric coordinates. > Is an internal point of the simplex if all its barycentric coordinates are strictly positive. > Otherwise, the closest point is internal to the sub-simplex corresponding to the positive coordinates, or is a vertex. > As a vector, it is orthogonal to the affine hull of this sub-simplex (if it’s not a vertex). >

Solving Barycentric Coordinates > The point x in the affine hull of points yi is closest to the origin if for an arbitrary yk > Thus, the vector x is orthogonal to n – 1 linearly independent vectors. These vectors span the linear space corresponding to the affine hull. >

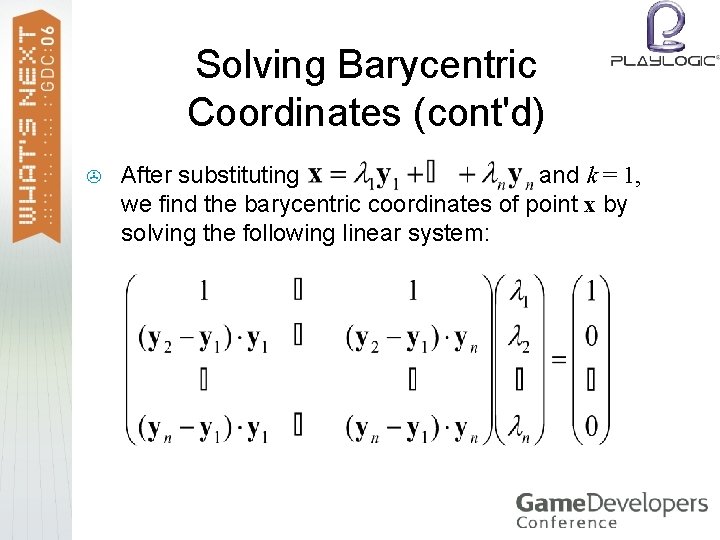
Solving Barycentric Coordinates (cont'd) > After substituting and k = 1, we find the barycentric coordinates of point x by solving the following linear system:

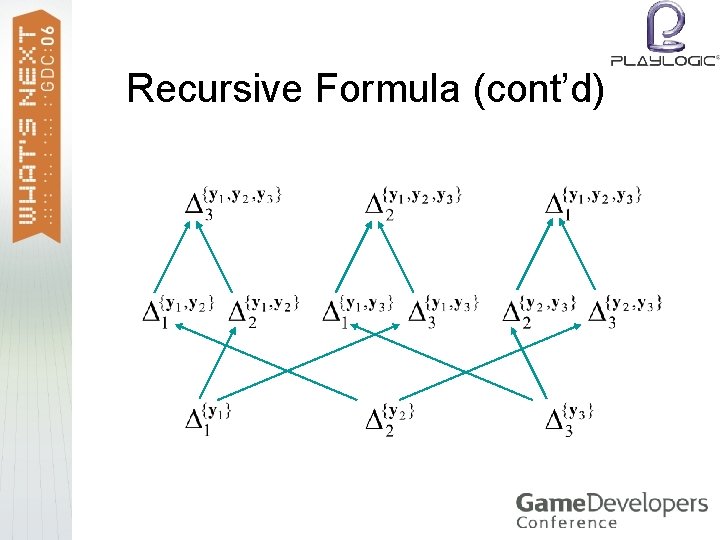
Recursive Formula > Cramer’s rule and other linear-algebra wizardry yield a recursive formulation of the solution: Here, IX denotes the set of indices of points in X.

Recursive Formula (cont’d)

Johnson’s Algorithm > > > Compute the determinants for all 2 n-1 sub-simplices (including the full simplex). The closest point of the simplex is the closest point of the unique sub-simplex X given by All vertices not in X are discarded in the next iteration of GJK.

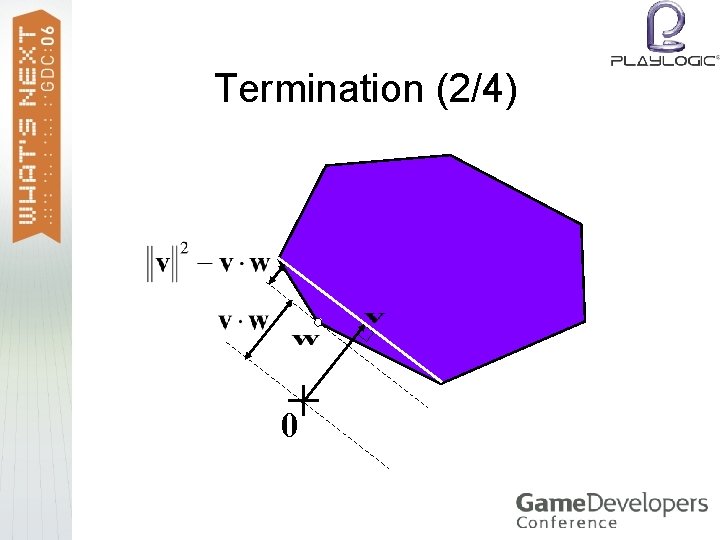
Termination (1/4) > > > As upper bound for the squared distance we take the squared length of v. As lower bound we take v∙w, the signed distance of the supporting plane through w. Terminate a soon as where εrel is the tolerance for the relative error in the computed distance.

Termination (2/4) + 0

Termination (3/4) > > In case of a (near) contact, v will approximate zero, in which case previous termination condition is not likely to be met. As secondary termination condition we use where v is the current closest point, W is the set of vertices of the current simplex, and εtol is a tolerance based on the machine epsilon.

Termination (4/4) > > > For objects that interpenetrate more extensively, GJK will eventually generate a tetrahedron containing the origin. We may terminate as soon as Johnson’s algorithm returns a tetrahedron, since the tetrahedron must contain the origin. In theory, the returned v should be zero, but normally it contains some rounding noise.

Numerical Issues (1/3) > > Determinant computation suffers from cancellation when the simplex is needle-shaped. Cancellation happens here: Rounding errors may cause Johnson’s algorithm to fail: No proper simplex can be found. The best thing to do is to simply terminate returning the last found distance.

Numerical Issues (2/3) > > > Noise in the computed v may result in failure to meet any of the termination conditions. GJK cycles returning the same support point or oscillates between two support points. Check whether the new support point is already a vertex of the current simplex (including discarded vertices). Each support point should be added only once, so a returning support point is a sure sign of trouble. Terminate as soon as this happens.

Numerical Issues (3/3) > > In order to be absolutely positively sure that GJK terminates in all cases add the following check. In theory, each new v should be shorter than the previous one, so terminate as soon as Here, εflt is the machine epsilon of the floatingpoint format.

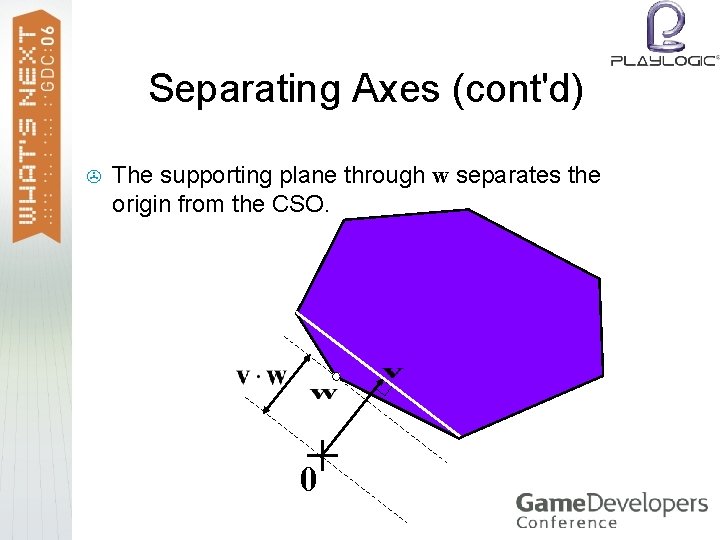
Separating Axes > > > If you only need to test for intersections then GJK may terminate as soon as v∙w becomes positive. For positive v∙w, the vector v is a separating axis. Separating axes can be cached and reused as initial v in future tests on the same object pairs. When the degree of frame coherence is high, the cached v is likely to be a separating axis in the new frame as well. An incremental version of GJK takes roughly one iteration per frame for smoothly moving objects.

Separating Axes (cont'd) > The supporting plane through w separates the origin from the CSO. + 0

Shape Casting > > Find the earliest time two translated objects come in contact. Boils down to performing a ray cast in the objects’ configuration space. For objects A and B being translated over respectively vectors s and t, we perform a ray cast along the vector r = t – s onto A – B. The earliest time of contact is

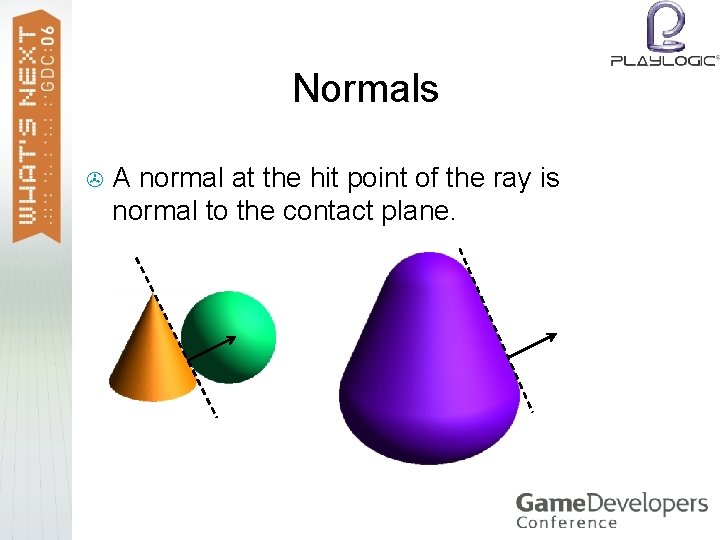
Normals > A normal at the hit point of the ray is normal to the contact plane.

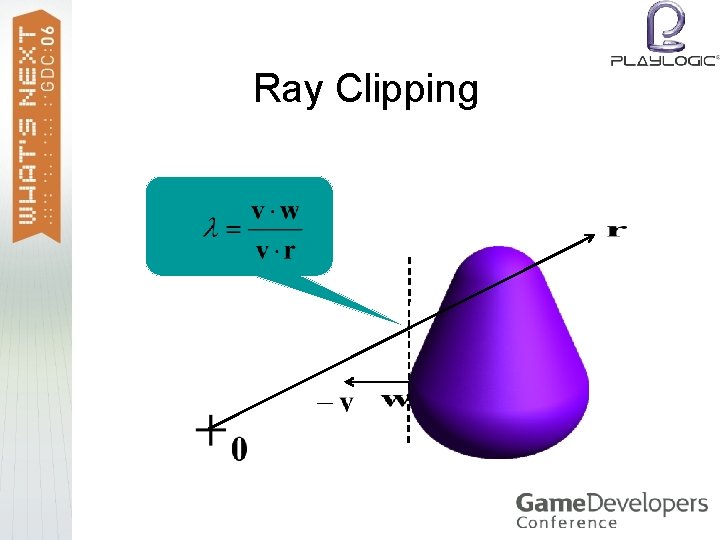
Ray Clipping

Ray Clipping (cont'd) > For , we know that If v∙r > 0 then λ is a lower bound for the hit spot, and if also v·w > 0, the ray is clipped. > If v·r < 0 then λ is an upper bound, and if also v·w > 0, then the ray misses. > If v·r = 0 and v·w > 0, the ray misses as well. >

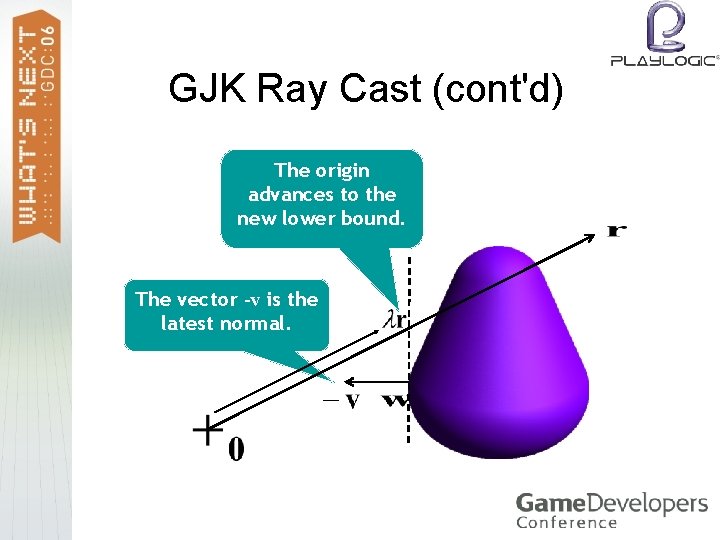
GJK Ray Cast Do a standard GJK iteration, and use the support planes as clipping planes. > Each time the ray is clipped, the origin is “shifted” to λr, … > …and the current simplex is set to the lastfound support point. > The vector -v that corresponds to the latest clipping plane is the normal at the hit point. >

GJK Ray Cast (cont'd) The origin advances to the new lower bound. The vector -v is the latest normal.

Termination > > > The origin advances only if v·w > 0, which must happen within a finite number of iterations if the origin is not contained in the query object. Terminate as soon as the origin is close enough to the query object, or we have evidence that the ray misses. As termination condition in case of a hit we use

Accuracy vs. Performance Accuracy can be traded for performance by tweaking the error tolerance εtol. > A greater tolerance results in fewer iterations but less accurate hit points and normals. >

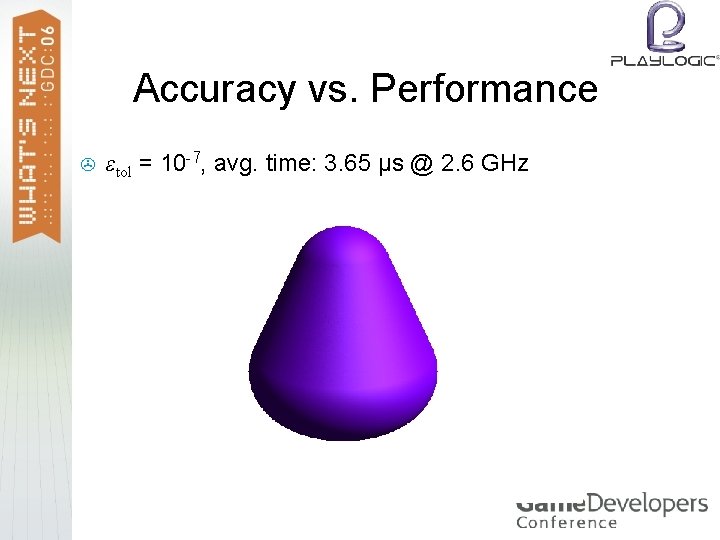
Accuracy vs. Performance > εtol = 10 -7, avg. time: 3. 65 μs @ 2. 6 GHz

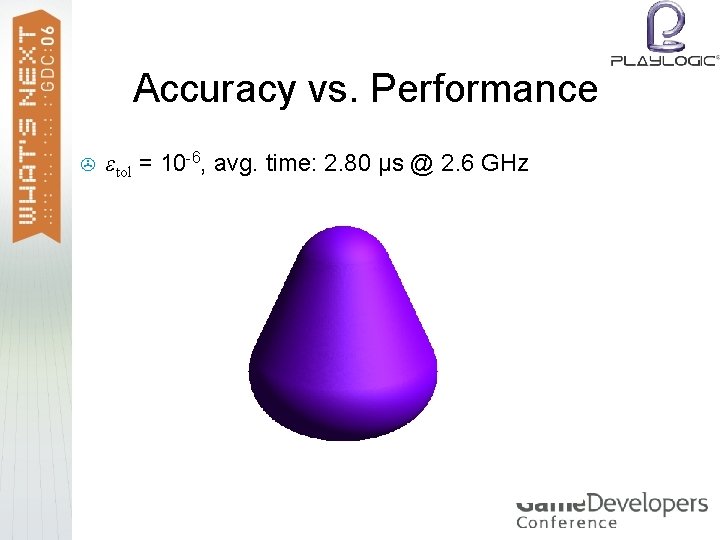
Accuracy vs. Performance > εtol = 10 -6, avg. time: 2. 80 μs @ 2. 6 GHz

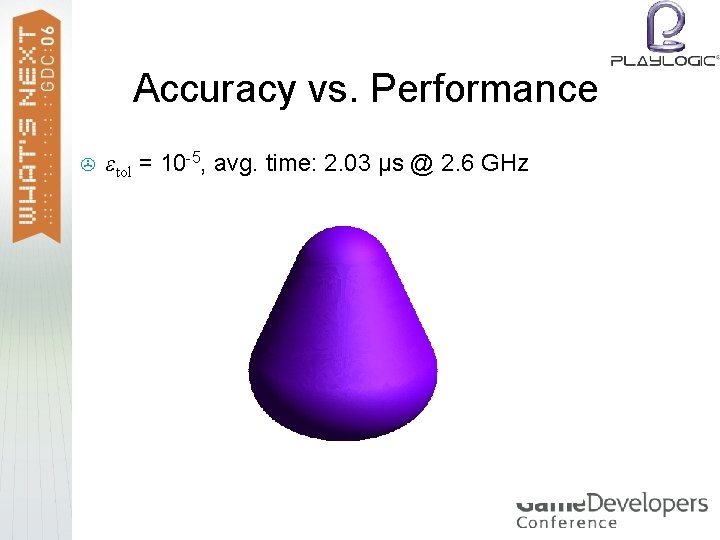
Accuracy vs. Performance > εtol = 10 -5, avg. time: 2. 03 μs @ 2. 6 GHz

Accuracy vs. Performance > εtol = 10 -4, avg. time: 1. 43 μs @ 2. 6 GHz

Accuracy vs. Performance > εtol = 10 -3, avg. time: 1. 02 μs @ 2. 6 GHz

Accuracy vs. Performance > εtol = 10 -2, avg. time: 0. 77 μs @ 2. 6 GHz

Accuracy vs. Performance > εtol = 10 -1, avg. time: 0. 62 μs @ 2. 6 GHz

Space-Time Sweep and Prune Find pairs of objects whose axis-aligned bounding boxes overlap. > Take translations of objects over the time interval into account. > No false positives: box pairs must overlap at some point in the time interval. >

AABB Computation > The projection of an object A onto an axis e is the interval: > Compute an object’s AABB by projecting the object onto the world axes.

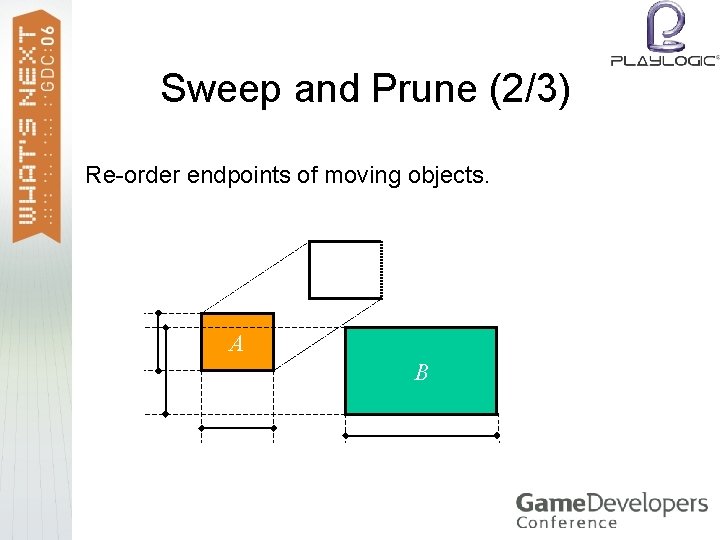
Sweep and Prune (1/3) For each world axis, maintain a sorted list of interval endpoints. > Maintain also the set of overlapping box pairs. > When a box moves, locally re-sort the lists by comparing and (if necessary) swapping the box endpoints with adjacent endpoints. >

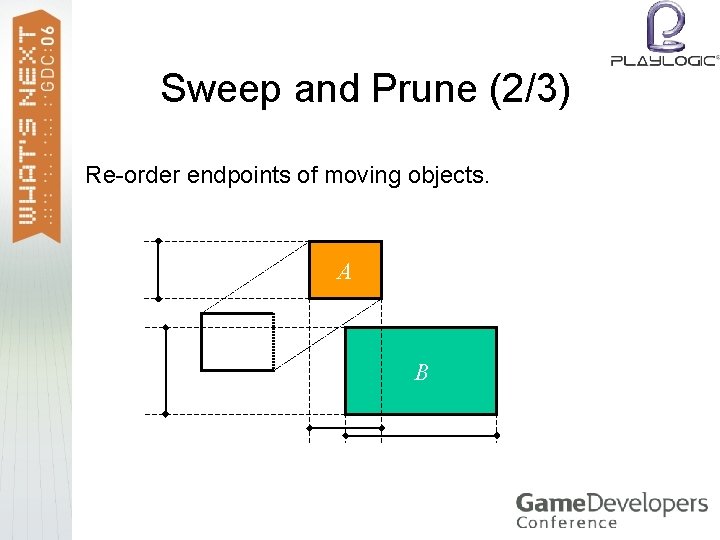
Sweep and Prune (2/3) Re-order endpoints of moving objects. A B

Sweep and Prune (2/3) Re-order endpoints of moving objects. A B

Sweep and Prune (3/3) When swapping “][“ to “[]”, the intervals start to overlap. > When swapping “[]“ to “][”, the intervals cease to overlap. > If the intervals on the other axes overlap, then the box pair starts or ceases to overlap. >

Implementation > “]” is greater than “[“ at equal positions Mangle the least-significant bit: 0 = “[”, 1 = “]”. > Beware of float sign! For negative numbers: 1 = “[”, 0 = “]”. > Better still: use fixed-point numbers for storing endpoint positions. > Integer comparisons are generally faster than float comparisons. >

Implementation (cont'd) > Endpoint lists are best implemented using arrays (std: : vector): Local sorting on arrays is CPU-cache friendly. > Each object maintains two indices per array. > Interval overlap tests can be done using array indices rather than endpoint positions. > > Use a hash table or a dictionary (std: : set) for storing the set of overlapping box pairs.

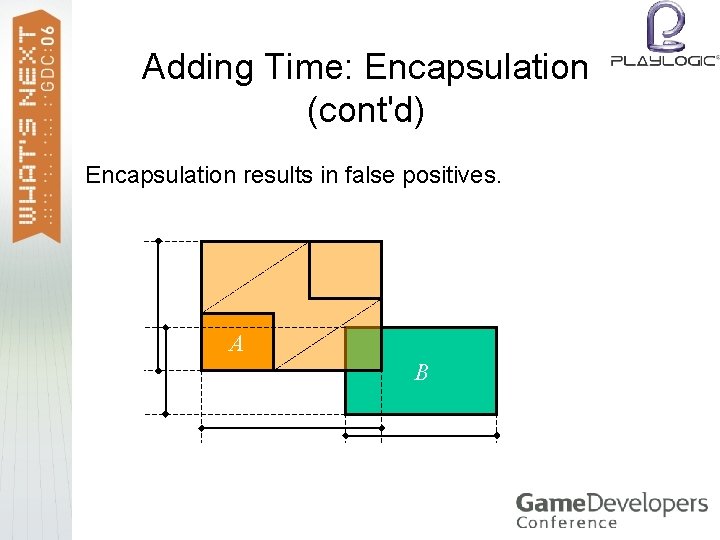
Adding Time: Encapsulation Enlarge AABBs of moving objects, such that they encapsulate the swept AABBs. > Creates false positives: Encapsulating AABBs overlap where in space-time, the actual AABBs do not. >

Adding Time: Encapsulation (cont'd) Encapsulation results in false positives. A B

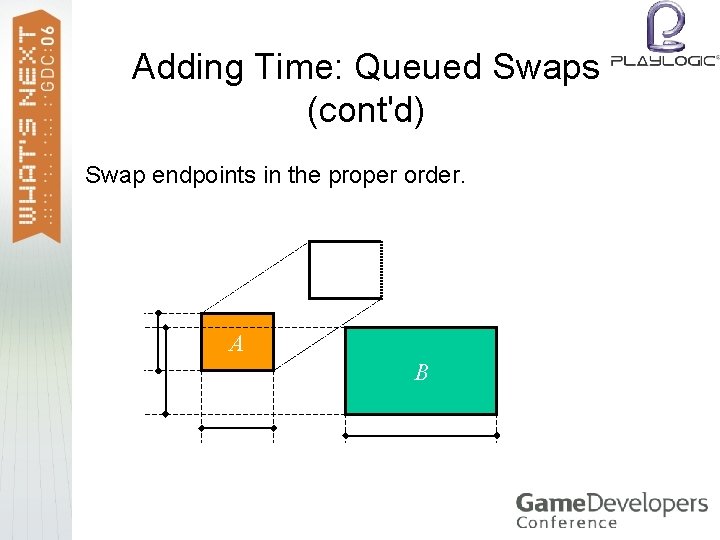
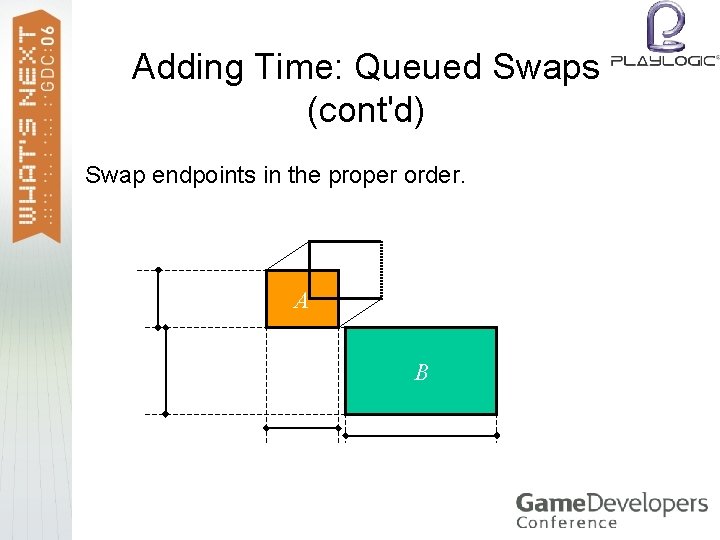
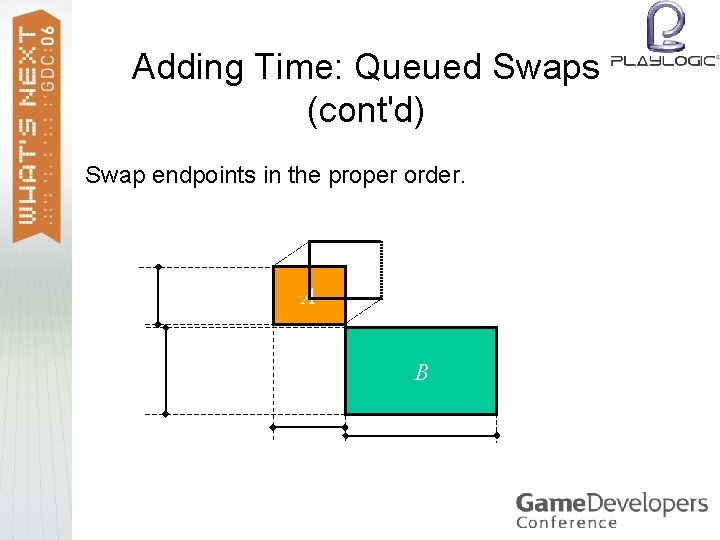
Adding Time: Queued Swaps Perform endpoint swaps in the proper order. > Calculate swap times and prioritize swaps on earliest time. > After each swap, re-evaluate swaps with new neighbors. > Needs a priority queue that offers a decrease-key operation (as in Dijkstra’s algorithm or A*). >

Adding Time: Queued Swaps (cont'd) Swap endpoints in the proper order. A B

Adding Time: Queued Swaps (cont'd) Swap endpoints in the proper order. A B

Adding Time: Queued Swaps (cont'd) Swap endpoints in the proper order. A B

Performance Queue operations dominate processing. > Despite added bookkeeping for decreasekey, best results so far are obtained using binary heaps. (Cormen et al. ). > Binomial heaps turned out slower due to expensive delete-min operation. > Still have to try Fibonacci heaps, relaxed heaps, skew heaps, pairing heaps, … >

Motion Coherence Space-time Sweep and Prune is often faster than the original version when many objects are moving in the same direction. > Among a group of objects all having the same velocity vector not a single endpoint swap needs to be done. > Ideal for particle and fluid simulations. >

Conclusion Exact continuous collision detection of convex objects under translation is doable in real time. > Unfortunately, exact continuous collision response is impossible in real-time. > Gino’s paradox (in the spirit of Zeno): “Continuous motion is an illusion since you cannot resolve an infinite number of collisions in a finite amount of time. ” >

References > > > Thomas H. Cormen et al. Introduction to Algorithms, Second Edition. MIT Press, 2001. E. G. Gilbert, D. W. Johnson, and S. S. Keerthi. A fast procedure for computing the distance between complex objects in three-dimensional space. IEEE Journal of Robotics and Automation, 4(2): 192 -203, 1988. Gino van den Bergen. Collision Detection in Interactive 3 D Environments. Morgan Kaufmann Publishers, 2004.

Thank You! > For papers and other information, check: www. dtecta. com > For information about Playlogic, please visit: www. playlogicgames. com