PHYSICS 220 Lecture 12 Collision and Explosion Lecture










- Slides: 21

PHYSICS 220 Lecture 12 Collision and Explosion Lecture 12 1

i. Clicker A railroad car is coasting along a horizontal track with speed v when it runs into and connects with a second identical railroad car, initially at rest. Assuming there is no friction between the cars and the rails, what is the speed of the two coupled cars after the collision? A) v B) v/2 C) v/4 D) 2 v S Pinitial = S Pfinal M v = M vf + M vf v = 2 vf vf = v/2 Lecture 12 2

Type of Collision • Elastic Collisions: – collisions that conserve mechanical energy • Inelastic Collisions: – collisions that do not conserve mechanical energy • Completely Inelastic Collisions: – objects stick together Elastic Lecture 12 Inelastic Completely Inelastic 3

Explosion Example: m 1 = M/3 m 2 = 2 M/3 v 1 “before” M m 1 m 2 v 2 “after” • Which block has larger |momentum|? * Each has same |momentum| • Which block has larger speed? * mv same for each smaller mass has larger velocity • Which block has larger kinetic energy? * K = mv 2/2 = m 2 v 2/2 m = p 2/2 m * smaller mass has larger kinetic energy • Is mechanical (kinetic) energy conserved? * NO Lecture 12 4

Explosion and Collision Explosion M m 1 m 2 Procedure “before” • Draw “before” and “after” • Define system so that Fext = 0 • Set up a coordinate system Collision m 1 Lecture 12 m 2 “before” “after” • Compute ptotal “before” • Compute ptotal “after” • Set them equal to each other 5

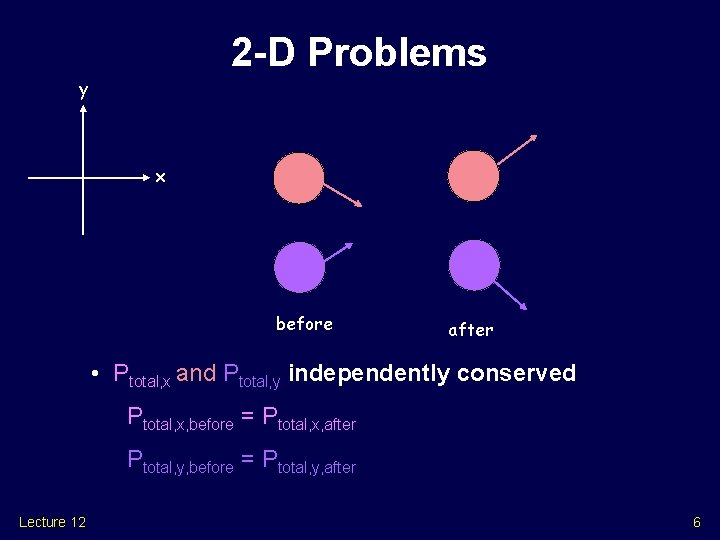
2 -D Problems y x before after • Ptotal, x and Ptotal, y independently conserved Ptotal, x, before = Ptotal, x, after Ptotal, y, before = Ptotal, y, after Lecture 12 6

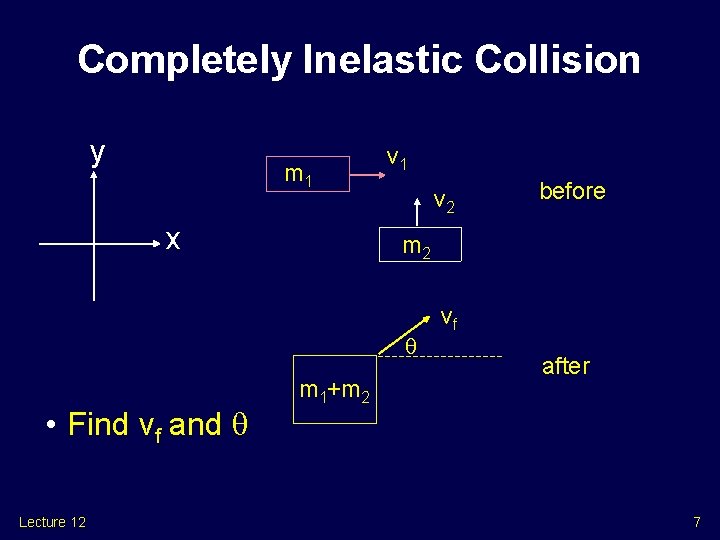
Completely Inelastic Collision y m 1 x v 1 v 2 m 2 • Find vf and Lecture 12 before m 1+m 2 vf after 7

Completely Inelastic Collision in Two Dimensions x • Find vf and y Lecture 12 m 1+m 2 vf after 8

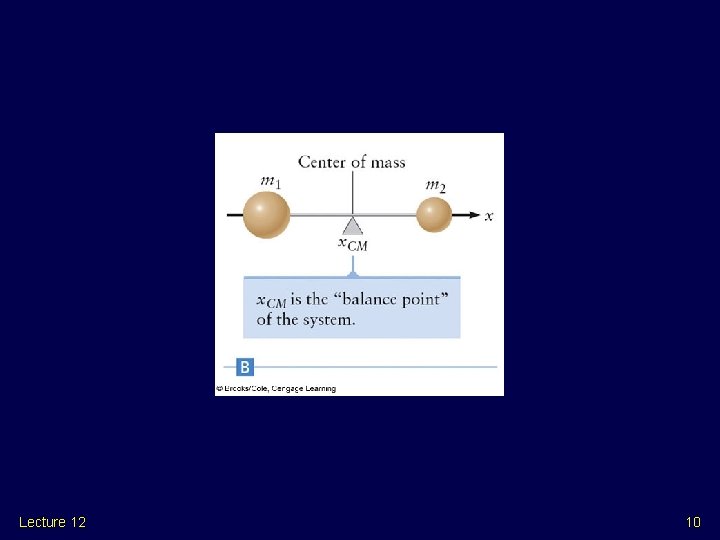
Center of Mass L Example 1: m m x. CM = (0 + m. L)/2 m = L/2 L Example 2: Lecture 12 m 5 m X=0 X=L x. CM = (0 + 5 m. L)/6 m = 5 L/6 9

Lecture 12 10

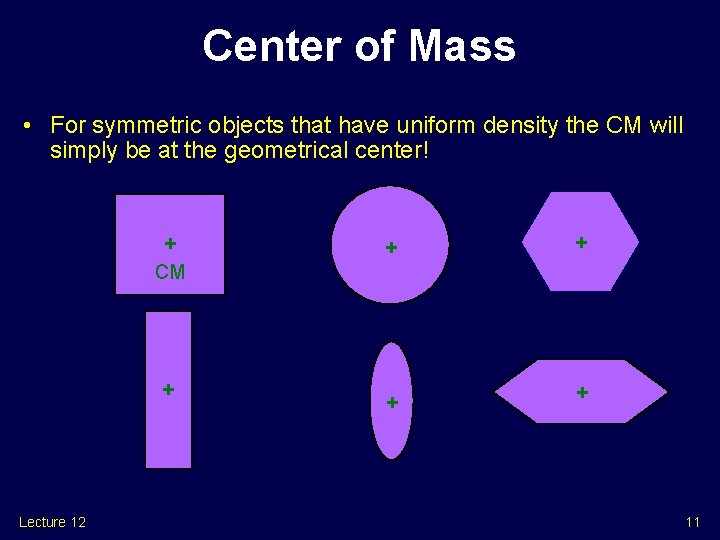
Center of Mass • For symmetric objects that have uniform density the CM will simply be at the geometrical center! + CM + Lecture 12 + + 11

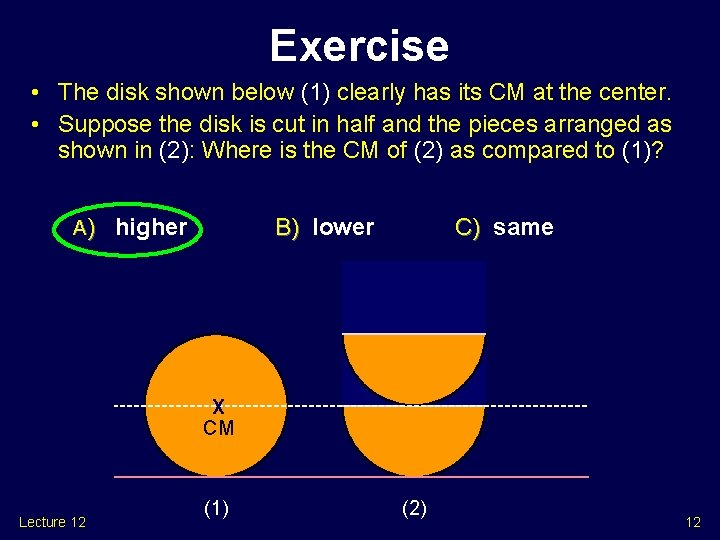
Exercise • The disk shown below (1) clearly has its CM at the center. • Suppose the disk is cut in half and the pieces arranged as shown in (2): Where is the CM of (2) as compared to (1)? A) higher B) lower C) same X CM Lecture 12 (1) (2) 12

Exercise • The CM of each half-disk will be closer to the fat end than to the thin end (think of where it would balance). l The CM of the compound object will be halfway between the CMs of the two halves. l This is higher than the CM of the disk X X CM (1) Lecture 12 X X (2) 13

Center of Mass Lecture 12 14

Dynamics of Many Particles ptot = mtot. Vcm Fext. Dt = Dptot = mtot. DVcm or Fext = mtotacm So if Fext = 0 then Vcm is constant • Center of Mass of a system behaves in a SIMPLE way - moves like a point particle! - velocity of CM is unaffected by collision if Fext = 0 Lecture 12 15

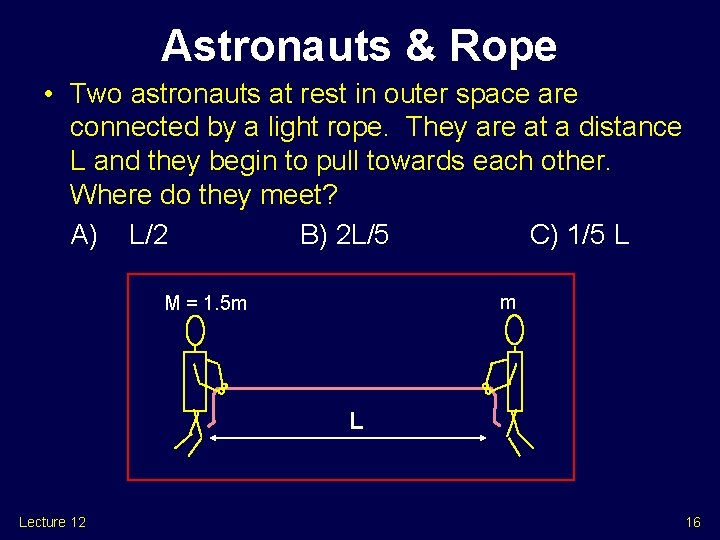
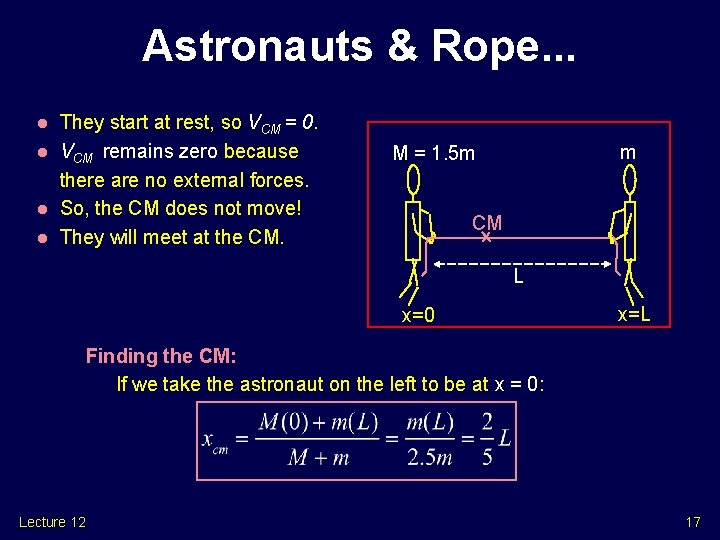
Astronauts & Rope • Two astronauts at rest in outer space are connected by a light rope. They are at a distance L and they begin to pull towards each other. Where do they meet? A) L/2 B) 2 L/5 C) 1/5 L m M = 1. 5 m L Lecture 12 16

Astronauts & Rope. . . l l They start at rest, so VCM = 0. VCM remains zero because there are no external forces. So, the CM does not move! They will meet at the CM. m M = 1. 5 m CM L x=0 x=L Finding the CM: If we take the astronaut on the left to be at x = 0: Lecture 12 17

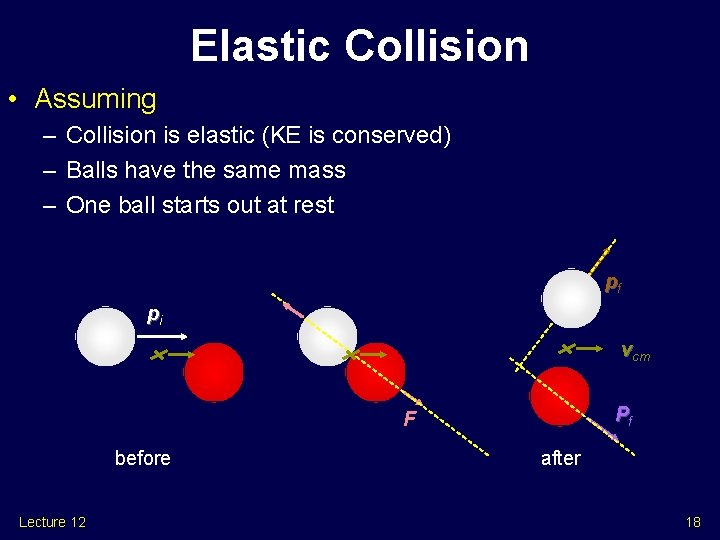
Elastic Collision • Assuming – Collision is elastic (KE is conserved) – Balls have the same mass – One ball starts out at rest pf pi vcm Pf F before Lecture 12 after 18

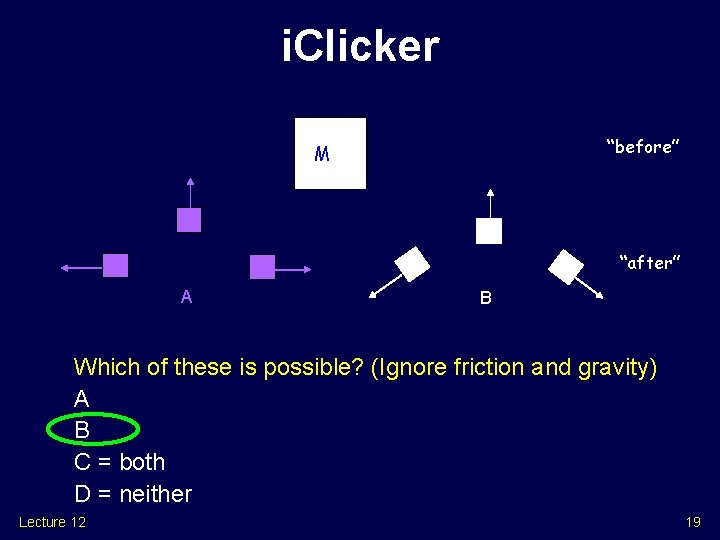
i. Clicker “before” M “after” A B Which of these is possible? (Ignore friction and gravity) A B C = both D = neither Lecture 12 19

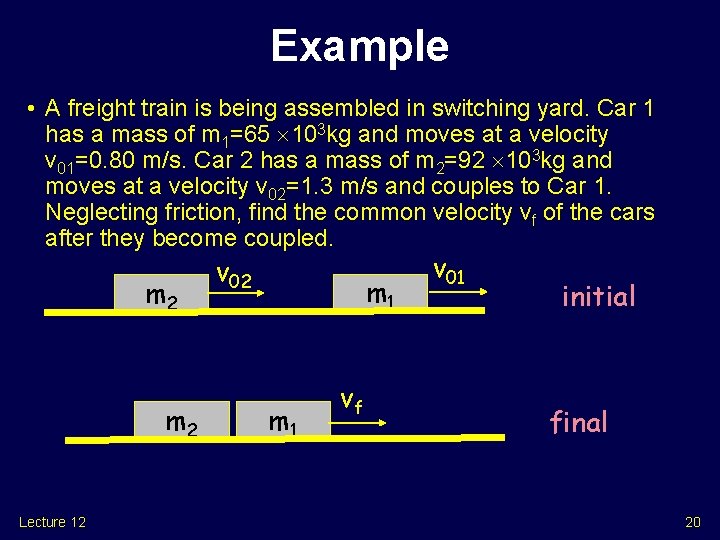
Example • A freight train is being assembled in switching yard. Car 1 has a mass of m 1=65 103 kg and moves at a velocity v 01=0. 80 m/s. Car 2 has a mass of m 2=92 103 kg and moves at a velocity v 02=1. 3 m/s and couples to Car 1. Neglecting friction, find the common velocity vf of the cars after they become coupled. m 2 Lecture 12 v 02 m 1 vf v 01 initial final 20

Example • A fright train is being assembled in switching yard. Car 1 has a mass of m 1=65 103 kg and moves at a velocity v 01=0. 80 m/s. Car 2 has a mass of m 2=92 103 kg and moves at a velocity v 02=1. 3 m/s and couples to it. Neglecting friction, find the common velocity vf of the cars after they become coupled. Apply conservation of momentum: Pi=m 1 vo 1+m 2 v 02 Pf=(m 1+m 2)vf = m 1 v 01+m 2 v 02 Lecture 12 21
 Explosion collision physics
Explosion collision physics Physics 220 purdue
Physics 220 purdue Collision physics
Collision physics Fall 2013
Fall 2013 Impulse and momentum
Impulse and momentum Raimond snellings
Raimond snellings 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Dow fire
Dow fire Physics 111 lecture notes
Physics 111 lecture notes Physics 101 lecture
Physics 101 lecture Physics 101 lecture 1
Physics 101 lecture 1 Physics 101 lecture notes pdf
Physics 101 lecture notes pdf Waves physics pdf
Waves physics pdf Atmospheric physics lecture notes
Atmospheric physics lecture notes The explosion larkin
The explosion larkin A famous author candy bar
A famous author candy bar Evangelism explosion outline
Evangelism explosion outline Definition population explosion
Definition population explosion Torpedo 48 shots
Torpedo 48 shots Thinking routine step inside
Thinking routine step inside Dmc cladding
Dmc cladding Mass explosion hazard placard
Mass explosion hazard placard